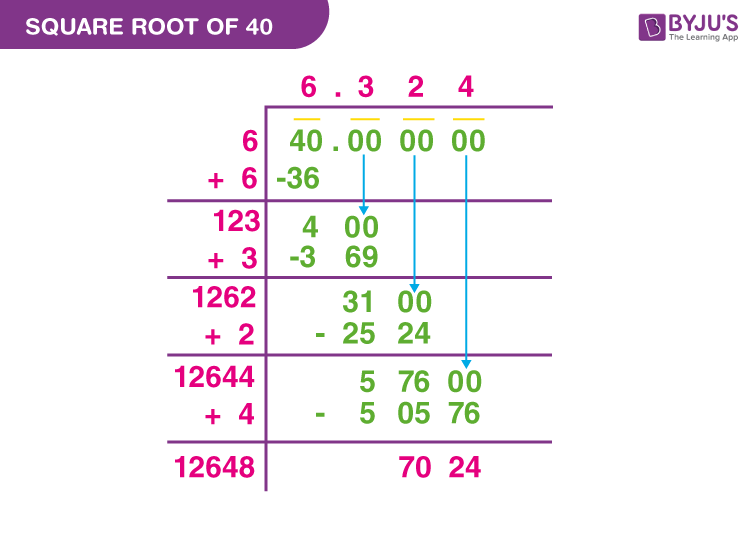
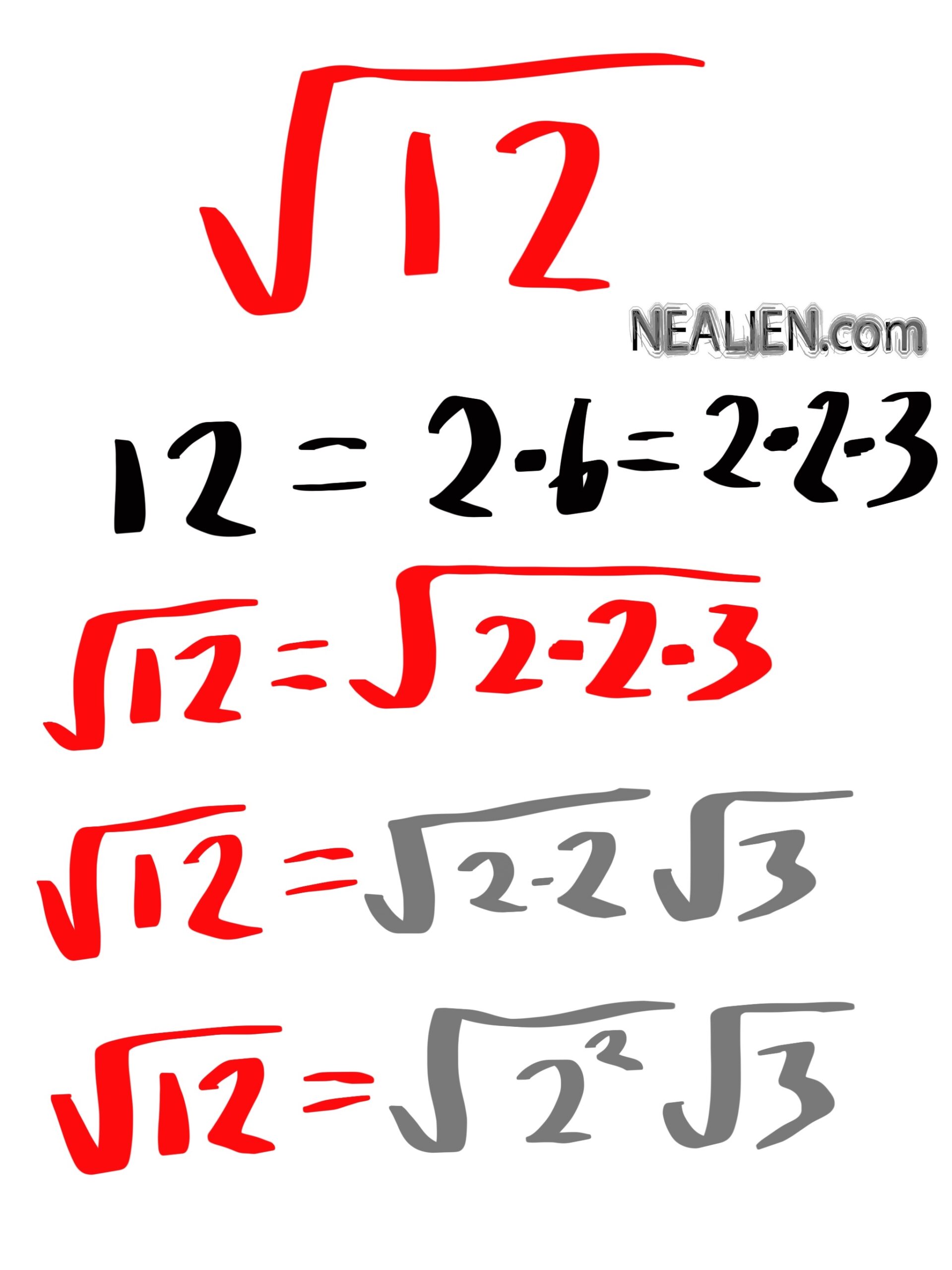Topic simplify square root calculator: Discover the power of the Simplify Square Root Calculator, your ultimate tool for effortlessly breaking down complex square roots into their simplest forms. Whether you’re a student or a math enthusiast, this guide will help you navigate the process with ease, ensuring accuracy and efficiency in your calculations.
Table of Content
- Simplify Square Root Calculator
- Introduction to Simplifying Square Roots
- Benefits of Using a Square Root Calculator
- How to Use a Simplify Square Root Calculator
- Step-by-Step Instructions
- Common Examples and Solutions
- Mathematical Background and Theory
- Prime Factorization Method
- Tips for Accurate Simplification
- Handling Complex Numbers
- Decimal and Fractional Square Roots
- Advanced Simplification Techniques
- Applications in Real Life
- FAQs about Square Root Simplification
- Resources and Further Reading
- YOUTUBE:
Simplify Square Root Calculator
Using a square root calculator can help simplify complex square roots into a more manageable form. This tool allows you to find the simplified radical form of any given square root.
Features
- Automatically simplifies square roots
- Handles both integers and decimals
- Displays results in radical form
- User-friendly interface
- Quick and accurate calculations
How to Use the Simplify Square Root Calculator
- Enter the number under the square root sign.
- Press the "Simplify" button.
- View the simplified square root in the results section.
Examples
| Input | Simplified Form |
|---|---|
| \(\sqrt{50}\) | \(5\sqrt{2}\) |
| \(\sqrt{72}\) | \(6\sqrt{2}\) |
| \(\sqrt{18}\) | \(3\sqrt{2}\) |
| \(\sqrt{45}\) | \(3\sqrt{5}\) |
Mathematical Background
The process of simplifying square roots involves factoring the number under the square root sign into its prime factors and then pairing the prime factors. Each pair of prime factors can be taken out of the square root as a single factor.
Formula
To simplify a square root, use the following formula:
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
Where a and b are factors of the number under the square root sign.
For example, to simplify \(\sqrt{72}\), you would factor 72 into \(36 \cdot 2\), then simplify as follows:
\(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\)
Using a calculator can speed up this process and ensure accuracy.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest radical form. This process is essential in mathematics to make calculations easier and more manageable. Understanding how to simplify square roots is beneficial for students, teachers, and anyone dealing with math-related tasks.
The basic idea is to break down the number under the square root into its prime factors and then simplify by removing pairs of factors from under the square root sign.
- Identify the number under the square root sign.
- Factor the number into its prime factors.
- Pair the prime factors.
- Move each pair of prime factors out from under the square root.
- Multiply the factors outside the square root sign.
- Combine any remaining factors inside the square root.
For example, to simplify \(\sqrt{72}\):
- Factor 72 into prime factors: \(72 = 2^3 \times 3^2\).
- Pair the prime factors: \(2^3 = 2 \times 2 \times 2\) and \(3^2 = 3 \times 3\).
- Take pairs out: \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2}\).
- Move each pair outside: \(2 \times 3 \times \sqrt{2}\).
- Simplify: \(\sqrt{72} = 6\sqrt{2}\).
Simplifying square roots helps in solving mathematical problems more efficiently, especially in algebra, geometry, and calculus. It also provides a clearer understanding of the properties of numbers and their relationships.
Benefits of Using a Square Root Calculator
Using a square root calculator offers numerous advantages, making the process of simplifying square roots easier, faster, and more accurate. Here are some key benefits:
- Accuracy: Calculators ensure precise results, eliminating the possibility of human error during calculations.
- Speed: Simplifying square roots manually can be time-consuming, especially with large numbers. A calculator provides instant results.
- User-Friendly: Modern calculators are designed with intuitive interfaces, making them accessible for users of all skill levels.
- Step-by-Step Solutions: Many calculators offer detailed steps for how the simplification is achieved, enhancing understanding and learning.
- Handling Complex Numbers: Advanced calculators can simplify square roots of both real and complex numbers.
- Versatility: Calculators can handle a wide range of inputs, including integers, decimals, and fractions.
- Educational Tool: They serve as excellent teaching aids, helping students grasp the concept of square roots and their simplification.
For example, to simplify \(\sqrt{200}\) using a calculator:
- Enter the number 200 into the calculator.
- Press the "Simplify" button.
- The calculator displays the simplified form: \(10\sqrt{2}\).
This process showcases the ease and efficiency of using a square root calculator. It saves time and effort, allowing users to focus on more complex aspects of their mathematical problems.
How to Use a Simplify Square Root Calculator
Using a simplify square root calculator is straightforward and can greatly enhance your mathematical efficiency. Here’s a detailed guide on how to use this tool effectively:
- Access the Calculator: Open your preferred square root calculator on a computer, smartphone, or tablet. Many calculators are available online for free.
- Enter the Number: Input the number you wish to simplify under the square root symbol. For instance, if you want to simplify \(\sqrt{50}\), type "50" into the calculator.
- Initiate the Calculation: Press the "Simplify" button or equivalent function on the calculator. This starts the simplification process.
- View the Results: The calculator will display the simplified form of the square root. For example, \(\sqrt{50}\) simplifies to \(5\sqrt{2}\).
- Review Step-by-Step Breakdown (if available): Some calculators provide a step-by-step explanation of how the simplification was achieved, which is useful for learning and verification.
For example, to simplify \(\sqrt{72}\):
- Enter "72" into the calculator.
- Press "Simplify."
- The calculator will display \(6\sqrt{2}\).
Using a simplify square root calculator is not only efficient but also educational. It helps users understand the process of simplification while ensuring accurate results.
Step-by-Step Instructions
Simplifying square roots manually can be a challenging task, but with the right approach, it becomes manageable. Here is a detailed step-by-step guide to help you simplify square roots effectively:
- Identify the Square Root: Determine the number under the square root that you need to simplify. For example, let’s simplify \(\sqrt{72}\).
- Factor the Number: Break down the number into its prime factors. In this case, \(72 = 2^3 \times 3^2\).
- Pair the Prime Factors: Group the prime factors into pairs. Here, \(2^3\) has one pair of 2s, and \(3^2\) has one pair of 3s.
- Extract the Pairs: Move each pair of factors outside the square root. Each pair of factors \((a \times a)\) can be written as a single factor \(a\) outside the square root.
- \(\sqrt{72} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)}\)
- Extract pairs: \(\sqrt{72} = 2 \times 3 \times \sqrt{2}\)
- Multiply the Extracted Factors: Multiply the factors that have been moved outside the square root. For this example, \(2 \times 3 = 6\).
- Simplify the Expression: Combine the simplified factors to get the final result. Thus, \(\sqrt{72} = 6\sqrt{2}\).
Another example is simplifying \(\sqrt{50}\):
- Identify the number: \(50\)
- Factor the number: \(50 = 2 \times 5^2\)
- Pair the factors: \(5^2\) has one pair of 5s
- Extract the pair: \(\sqrt{50} = 5\sqrt{2}\)
By following these steps, you can simplify any square root efficiently. Using a calculator can further speed up the process and ensure accuracy.

Common Examples and Solutions
Simplifying square roots is a fundamental skill in mathematics. Here are some common examples and detailed solutions to help you understand the process:
Example 1: Simplify \(\sqrt{50}\)
- Identify the number: \(50\)
- Factor the number into its prime factors: \(50 = 2 \times 5^2\)
- Group the prime factors into pairs: \(5^2\) has one pair of 5s
- Move each pair outside the square root: \(\sqrt{50} = 5\sqrt{2}\)
- The simplified form is: \(5\sqrt{2}\)
Example 2: Simplify \(\sqrt{72}\)
- Identify the number: \(72\)
- Factor the number into its prime factors: \(72 = 2^3 \times 3^2\)
- Group the prime factors into pairs: \(2^3\) has one pair of 2s, \(3^2\) has one pair of 3s
- Move each pair outside the square root: \(\sqrt{72} = 2 \times 3 \times \sqrt{2}\)
- Multiply the factors outside the square root: \(2 \times 3 = 6\)
- The simplified form is: \(6\sqrt{2}\)
Example 3: Simplify \(\sqrt{18}\)
- Identify the number: \(18\)
- Factor the number into its prime factors: \(18 = 2 \times 3^2\)
- Group the prime factors into pairs: \(3^2\) has one pair of 3s
- Move each pair outside the square root: \(\sqrt{18} = 3\sqrt{2}\)
- The simplified form is: \(3\sqrt{2}\)
Example 4: Simplify \(\sqrt{45}\)
- Identify the number: \(45\)
- Factor the number into its prime factors: \(45 = 3^2 \times 5\)
- Group the prime factors into pairs: \(3^2\) has one pair of 3s
- Move each pair outside the square root: \(\sqrt{45} = 3\sqrt{5}\)
- The simplified form is: \(3\sqrt{5}\)
These examples illustrate the steps needed to simplify square roots. By practicing these steps, you will become more proficient in simplifying square roots and handling more complex mathematical problems.
Mathematical Background and Theory
Simplifying square roots is grounded in fundamental mathematical principles. Understanding these principles helps in mastering the simplification process. Here’s a detailed explanation of the mathematical background and theory:
Square Roots and Radicals
The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). This is represented as \(\sqrt{x}\). For example, \(\sqrt{9} = 3\) because \(3 \times 3 = 9\).
Prime Factorization
Prime factorization involves breaking down a number into its prime factors. Prime numbers are numbers greater than 1 that have no positive divisors other than 1 and themselves.
- Example: The prime factorization of 72 is \(2^3 \times 3^2\).
Properties of Square Roots
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \(\sqrt{a^2} = a\)
Simplification Process
To simplify a square root, follow these steps:
- Factor the Number: Find the prime factorization of the number under the square root. For instance, for \(\sqrt{72}\), factorize 72 to get \(2^3 \times 3^2\).
- Pair the Factors: Group the prime factors into pairs. Each pair of factors can be moved outside the square root as a single factor. For \(\sqrt{72}\), this means \(\sqrt{(2 \times 2) \times 2 \times (3 \times 3)} = 2 \times 3 \times \sqrt{2}\).
- Simplify: Multiply the factors outside the square root to get the simplified form. Thus, \(\sqrt{72} = 6\sqrt{2}\).
Examples
Here are a few examples demonstrating the simplification process:
| Expression | Prime Factorization | Pairs | Simplified Form |
|---|---|---|---|
| \(\sqrt{50}\) | 2, \(5^2\) | Pair of 5s | \(5\sqrt{2}\) |
| \(\sqrt{72}\) | \(2^3, 3^2\) | Pair of 2s, Pair of 3s | \(6\sqrt{2}\) |
| \(\sqrt{45}\) | \(3^2, 5\) | Pair of 3s | \(3\sqrt{5}\) |
By understanding these mathematical concepts and following the steps outlined, simplifying square roots becomes a systematic and straightforward process.
Prime Factorization Method
The prime factorization method is a reliable approach for simplifying square roots. This method involves breaking down the number under the square root into its prime factors and then simplifying. Here’s a detailed step-by-step guide on using the prime factorization method:
Step-by-Step Process
- Identify the Number: Determine the number you need to simplify. For example, let's simplify \(\sqrt{180}\).
- Find the Prime Factors: Break down the number into its prime factors.
- 180 can be factored as \(180 = 2^2 \times 3^2 \times 5\).
- Group the Prime Factors: Organize the prime factors into pairs.
- In \(2^2 \times 3^2 \times 5\), you have pairs of 2s and pairs of 3s.
- Extract Pairs: Move each pair of prime factors outside the square root.
- \(\sqrt{180} = \sqrt{(2 \times 2) \times (3 \times 3) \times 5}\)
- \(\sqrt{180} = 2 \times 3 \times \sqrt{5}\)
- Multiply the Extracted Factors: Multiply the factors outside the square root.
- \(2 \times 3 = 6\)
- Simplify the Expression: Combine the simplified factors to get the final result.
- \(\sqrt{180} = 6\sqrt{5}\)
Additional Examples
Here are more examples to illustrate the prime factorization method:
| Expression | Prime Factorization | Pairs | Simplified Form |
|---|---|---|---|
| \(\sqrt{98}\) | \(2 \times 7^2\) | Pair of 7s | \(7\sqrt{2}\) |
| \(\sqrt{150}\) | \(2 \times 3 \times 5^2\) | Pair of 5s | \(5\sqrt{6}\) |
| \(\sqrt{200}\) | \(2^3 \times 5^2\) | Pair of 2s, Pair of 5s | \(10\sqrt{2}\) |
The prime factorization method is effective because it simplifies the process into manageable steps, ensuring accuracy and clarity. By practicing this method, you can easily simplify any square root.
Tips for Accurate Simplification
Simplifying square roots accurately is crucial for solving mathematical problems effectively. Here are some detailed tips to help you simplify square roots accurately:
- Understand the Basics: Ensure you have a solid understanding of what a square root is and how it functions. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \).
- Use Prime Factorization: Break down the number inside the square root into its prime factors. This helps in identifying pairs of factors for simplification. For example, for \( \sqrt{72} \):
- Find the prime factors of 72: \( 72 = 2^3 \times 3^2 \)
- Pair the factors: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 3^2) \times 2} \)
- Simplify the pairs: \( \sqrt{(2^2 \times 3^2) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
- Look for Perfect Squares: Identify perfect square factors within the number. Perfect squares are numbers like 1, 4, 9, 16, etc., which have integer square roots.
- Use the Property of Square Roots: Utilize the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) to break down complex square roots into simpler parts.
- Double-Check Your Work: Verify your simplifications by squaring the simplified form to see if you get back the original number. For example, if \( \sqrt{50} \) simplifies to \( 5\sqrt{2} \), check by calculating \( (5\sqrt{2})^2 = 50 \).
- Handle Fractions Carefully: When simplifying square roots of fractions, simplify the numerator and the denominator separately. For example, \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \).
- Use a Calculator for Verification: While manual simplification is important for understanding, using a square root calculator can help verify your results quickly and accurately.
- Practice Regularly: Regular practice with different types of square roots will improve your accuracy and speed. Try simplifying a variety of square roots to become more proficient.
By following these tips, you can simplify square roots more accurately and efficiently, aiding in your overall mathematical problem-solving skills.

Handling Complex Numbers
When dealing with square roots of negative numbers, we enter the realm of complex numbers. Complex numbers are numbers that have both a real part and an imaginary part. The imaginary unit is denoted by \(i\), where \(i\) is defined as:
\[ i = \sqrt{-1} \]
This definition allows us to express the square root of any negative number. For example:
\[ \sqrt{-4} = \sqrt{4 \cdot -1} = \sqrt{4} \cdot \sqrt{-1} = 2i \]
Here are some tips for accurately handling complex numbers when simplifying square roots:
- Identify Negative Radicands: When the number under the square root (radicand) is negative, recognize that the result will involve the imaginary unit \(i\).
- Separate the Radicand: Decompose the radicand into a product of a positive number and \(-1\). For example, for \(\sqrt{-50}\), write it as \(\sqrt{50 \cdot -1}\).
-
Use the Imaginary Unit: Simplify the square root of the positive part and multiply by \(i\). For \(\sqrt{-50}\):
\[ \sqrt{-50} = \sqrt{50} \cdot \sqrt{-1} = \sqrt{25 \cdot 2} \cdot i = 5\sqrt{2}i \] -
Complex Conjugates: For complex numbers, remember that multiplying a complex number by its conjugate results in a real number. The conjugate of \(a + bi\) is \(a - bi\). For example:
\[ (3 + 4i)(3 - 4i) = 3^2 - (4i)^2 = 9 - 16(-1) = 9 + 16 = 25 \] - Simplify Step-by-Step: When dealing with more complex expressions, simplify the real and imaginary parts separately before combining them.
These steps will help ensure accurate simplification when working with square roots of negative numbers and complex expressions. Utilizing tools such as a simplify square root calculator can also aid in verifying your results and providing step-by-step solutions.
Decimal and Fractional Square Roots
Simplifying square roots involving decimals and fractions can be a bit tricky, but with the right approach, it becomes manageable. Here are some detailed tips and step-by-step instructions to help you simplify square roots of decimals and fractions:
Simplifying Decimal Square Roots
To simplify the square root of a decimal, you can convert the decimal to a fraction first and then simplify:
- Convert the decimal to a fraction. For example, 0.25 can be written as \( \frac{25}{100} \).
- Reduce the fraction to its simplest form. In this case, \( \frac{25}{100} = \frac{1}{4} \).
- Take the square root of the numerator and the denominator separately: \( \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \).
Therefore, \( \sqrt{0.25} = 0.5 \).
Simplifying Fractional Square Roots
Simplifying the square root of a fraction involves a similar process:
- Write the fraction under the square root symbol. For example, \( \sqrt{\frac{9}{16}} \).
- Take the square root of the numerator and the denominator separately: \( \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \).
Therefore, \( \sqrt{\frac{9}{16}} = \frac{3}{4} \).
Examples and Practice
- Example 1: \( \sqrt{0.04} \)
- Convert 0.04 to a fraction: \( \frac{4}{100} \)
- Simplify the fraction: \( \frac{1}{25} \)
- Take the square root: \( \sqrt{\frac{1}{25}} = \frac{1}{5} \)
So, \( \sqrt{0.04} = 0.2 \).
- Example 2: \( \sqrt{\frac{49}{64}} \)
- Take the square root of the numerator and the denominator separately: \( \sqrt{\frac{49}{64}} = \frac{\sqrt{49}}{\sqrt{64}} = \frac{7}{8} \)
So, \( \sqrt{\frac{49}{64}} = \frac{7}{8} \).
General Tips
- When dealing with decimals, always try to convert them to fractions for easier simplification.
- Remember the property \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), which allows you to handle the numerator and the denominator separately.
- Practice with different examples to become more comfortable with the process.
Advanced Simplification Techniques
When dealing with square roots, advanced simplification techniques can help in handling more complex expressions efficiently. Here are some advanced methods to simplify square roots:
-
Prime Factorization:
Factor the number inside the square root into its prime factors and simplify by pairing identical factors.
- Example: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} = 6\sqrt{2} \)
-
Rationalizing the Denominator:
If a square root appears in the denominator of a fraction, multiply both the numerator and the denominator by the square root to eliminate it.
- Example: \( \frac{1}{\sqrt{2}} = \frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2} \)
-
Handling Nested Radicals:
Simplify nested square roots by expressing them in terms of simpler radicals.
- Example: \( \sqrt{\sqrt{16}} = \sqrt{4} = 2 \)
-
Combining Radicals:
Use the property \( \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \) to combine or separate radicals as needed.
- Example: \( \sqrt{2} \times \sqrt{8} = \sqrt{16} = 4 \)
-
Advanced Factoring:
For higher-order roots, use the least common multiple (LCM) of the exponents to simplify the expression.
- Example: \( \sqrt[4]{16} = \sqrt[4]{2^4} = 2 \)
-
Using Calculators:
Online calculators can be a valuable tool for performing complex simplifications quickly. These tools often provide step-by-step solutions to help understand the process.
- Example: Inputting \( \sqrt{50} \) into a simplification calculator might yield \( 5\sqrt{2} \) with an explanation of each step.
By mastering these advanced techniques, you can simplify even the most challenging square root expressions with confidence and accuracy.
Applications in Real Life
Square roots play a crucial role in various real-life applications. Here are some key areas where they are essential:
- Engineering and Architecture: Square roots are used in engineering and architecture to calculate dimensions, areas, and volumes. They help in determining the lengths of sides in right-angled triangles using the Pythagorean theorem.
- Physics: In physics, square roots are used to solve equations involving energy, wave functions, and other phenomena. For instance, the root mean square (RMS) value in AC circuits is derived using square roots.
- Statistics: Square roots are used to calculate standard deviations, which measure the amount of variation or dispersion in a set of values.
- Finance: Square roots are used in finance to calculate volatility and the standard deviation of returns on investment portfolios.
- Computer Graphics: In computer graphics, square roots are used to calculate distances and magnitudes, essential for rendering images and animations.
- Astronomy: Square roots are used in calculating distances between celestial bodies and their gravitational forces.
- Medicine: In medical imaging, square roots are used in algorithms for reconstructing images from X-ray or MRI data.
- Construction: Square roots are used to ensure structures are level and properly aligned, such as in laying out foundations or ensuring walls are perpendicular.
Understanding the applications of square roots in these areas highlights their importance in both theoretical and practical aspects of various fields.

FAQs about Square Root Simplification
-
What is square root simplification?
Square root simplification involves reducing a square root to its simplest form. This is typically done by finding the largest square factor of the number under the square root and then factoring it out.
-
How do I simplify a square root?
To simplify a square root, follow these steps:
- Find the prime factorization of the number under the square root.
- Group the prime factors into pairs.
- Move each pair of prime factors outside the square root as a single factor.
- Multiply the factors outside the square root together.
- Keep any remaining factors inside the square root.
For example, to simplify \( \sqrt{72} \):
- Prime factorization: \( 72 = 2^3 \times 3^2 \)
- Grouping pairs: \( 2^3 \) has one pair of 2s, and \( 3^2 \) has one pair of 3s.
- Moving pairs outside: \( \sqrt{72} = \sqrt{2^2 \times 2 \times 3^2} = 2 \times 3 \sqrt{2} = 6\sqrt{2} \)
-
Can you simplify square roots of negative numbers?Yes, the square root of a negative number involves imaginary numbers. The square root of -1 is denoted as \( i \). For example, \( \sqrt{-4} = 2i \).
-
How do you handle square roots in fractions?
To simplify square roots in fractions:
- If the fraction is \( \frac{\sqrt{a}}{\sqrt{b}} \), simplify it as \( \sqrt{\frac{a}{b}} \) if possible.
- If there is a square root in the denominator, rationalize the denominator by multiplying the numerator and denominator by the square root in the denominator.
Example: \( \frac{1}{\sqrt{2}} \) can be rationalized to \( \frac{\sqrt{2}}{2} \).
-
Why is simplifying square roots important?Simplifying square roots is important for:
- Making mathematical expressions easier to work with.
- Solving equations more efficiently.
- Improving accuracy in calculations.
-
Are there tools available to simplify square roots?Yes, there are various online calculators and tools that can simplify square roots and provide step-by-step solutions, such as those available on Omni Calculator and Mathway.
Resources and Further Reading
For those who wish to delve deeper into the topic of simplifying square roots, here are some valuable resources and further reading materials:
- - This online tool helps simplify square roots and provides step-by-step instructions for various problems.
- - A user-friendly calculator that explains and solves square root problems in the simplest form.
- - An advanced calculator that uses various properties of radicals to simplify expressions effectively.
- - Comprehensive videos and tutorials that explain the concepts of simplifying square roots and radicals in an easy-to-understand manner.
- - A resource that breaks down the concept of simplifying square roots with clear explanations and examples.
These resources will provide you with a solid foundation and additional practice in simplifying square roots, making it easier to understand and apply these concepts in various mathematical contexts.
Đơn giản hóa căn bậc hai với máy tính đồ thị
READ MORE:
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Căn Bậc Hai