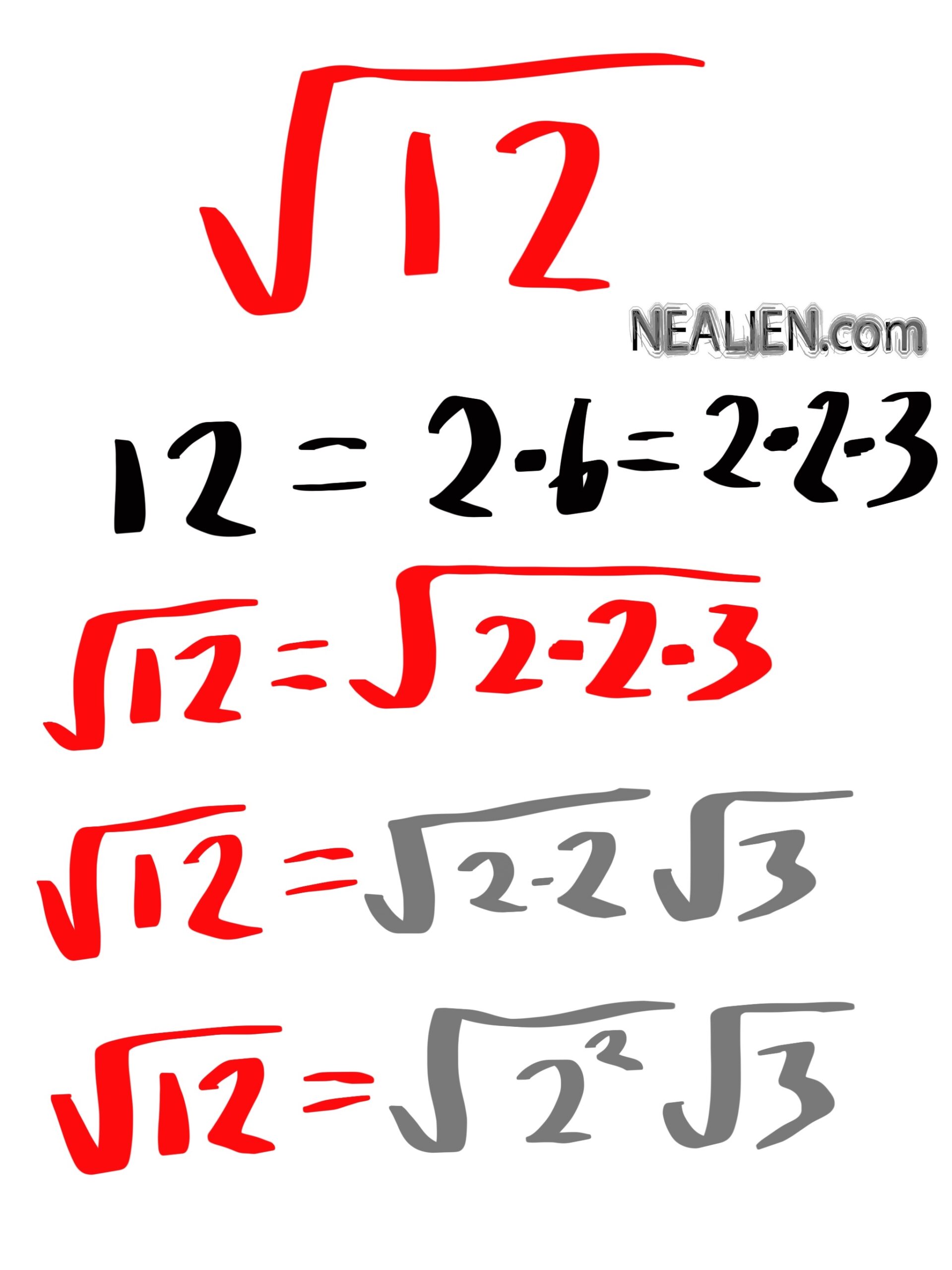Square Root 84 Simplified: Easy Steps to Understand and Solve

To simplify the square root of 84, we need to find the prime factorization of 84 and then simplify using these factors.

Prime Factorization

The prime factorization of 84 is:

So, we can rewrite 84 as:

Simplifying the Square Root

We can simplify this by taking out the square root of the perfect square:

This simplifies to:

Conclusion

Therefore, the simplified form of the square root of 84 is:

Square roots are fundamental concepts in mathematics, often encountered in various fields such as algebra, geometry, and calculus. Understanding square roots is essential for solving equations, simplifying expressions, and comprehending more advanced mathematical theories.

A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\).

Here are the steps to find and simplify square roots:

1. Identify the number you need to find the square root of.
2. Determine its prime factors.
3. Pair the prime factors.
4. Take one factor from each pair outside the square root.
5. Multiply the factors outside the square root.
6. Simplify the remaining expression inside the square root if possible.

For example, to simplify the square root of 84:

• Prime factorization of 84: \(84 = 2 \times 2 \times 3 \times 7\)
• Pair the factors: \(2 \times 2\)
• Take one factor from the pair outside the square root: \(2\)
• Multiply the factors outside: \(2\)
• The remaining inside the square root: \(3 \times 7 = 21\)

Thus, the square root of 84 simplified is:

Understanding and simplifying square roots is crucial for solving complex mathematical problems and is a skill that enhances your overall mathematical abilities.

To fully understand the square root of 84, it is important to grasp the concept of square roots and the methods used to simplify them. The square root of a number is a value that, when multiplied by itself, results in the original number. For example, the square root of 25 is 5, because \(5 \times 5 = 25\).

Let's delve into the process of simplifying the square root of 84 step by step:

1. Identify the Number: We are working with the number 84.
2. Prime Factorization: Break down 84 into its prime factors.
   • 84 is an even number, so we start with 2: \(84 \div 2 = 42\)
   • 42 is also even, divide by 2: \(42 \div 2 = 21\)
   • 21 is divisible by 3: \(21 \div 3 = 7\)
   • 7 is a prime number.

   Therefore, the prime factorization of 84 is:

   $84=2\times 2\times 3\times 7$
3. Pair the Factors: Identify pairs of prime factors.

   From the prime factorization \(2 \times 2 \times 3 \times 7\), we can pair the twos.

4. Simplify: Take one factor from each pair outside the square root.

   The pair of twos (2²) can be taken out as a single 2.

5. Combine: Multiply the factors outside the square root and simplify the remaining expression.

   This gives us:

   $\sqrt{2²\times 3\times 7}=2\times \sqrt{3\times 7}=2\surd 21$

Therefore, the simplified form of the square root of 84 is:

Understanding this process not only helps in simplifying square roots but also enhances your overall problem-solving skills in mathematics.

The prime factorization method is a systematic approach to breaking down a composite number into its prime factors. Prime factors are the prime numbers that multiply together to give the original number. This method is especially useful in simplifying square roots. Let's apply this method to the number 84.

1. Start with the Number: Begin with the number you want to factorize, in this case, 84.
2. Divide by the Smallest Prime: Check if the number is divisible by the smallest prime number, which is 2. Since 84 is even, it is divisible by 2.
   • \(84 \div 2 = 42\)
3. Continue Factoring: Continue dividing the quotient by the smallest prime number until it is no longer divisible by that prime.
   • 42 is also even, so divide by 2: \(42 \div 2 = 21\)
4. Move to the Next Prime: Once the number is no longer divisible by 2, move to the next smallest prime number, which is 3.
   • 21 is divisible by 3: \(21 \div 3 = 7\)
5. Factor the Remaining Number: The quotient is now 7, which is a prime number.
   • 7 is already a prime factor.

Therefore, the prime factorization of 84 is:

To verify, we can multiply these prime factors back together:

Using the prime factorization method, we can simplify the square root of 84 by pairing the prime factors and simplifying as follows:

Thus, the square root of 84 simplified is \(2\sqrt{21}\), thanks to the prime factorization method.

Simplifying square roots involves reducing the square root to its simplest form. This process can be achieved by identifying the factors of the number under the square root, especially focusing on perfect squares. Here is a step-by-step guide to simplifying square roots, using the square root of 84 as an example.

1. Identify the Number: Start with the number you want to simplify, in this case, 84.
2. Prime Factorization: Break down the number into its prime factors.
   • 84 can be factorized as follows: \(84 = 2 \times 2 \times 3 \times 7\)
3. Group the Factors: Pair the prime factors into groups of two.
   • In \(84 = 2 \times 2 \times 3 \times 7\), we can group the twos together.
4. Simplify the Square Root: Take one factor from each pair outside the square root.

   For the pair of twos:
   $$
   
   
   
   2
   ²
   ×
   3
   ×
   7
   
   
   =
   2
   ×
   
   
   3
   ×
   7
   
   
   
   

5. Combine the Factors: Multiply the factors outside the square root.

   The simplified form of the square root of 84 is:
   $$
   
   2
   √
   21
   
   

This process can be applied to any number to simplify its square root. By identifying and grouping the prime factors, you can take advantage of perfect squares to make the expression simpler and more manageable.

Here are additional examples to further illustrate the method:

• Example 1: Simplify \(\sqrt{50}\)
  1. Prime factorization: \(50 = 2 \times 5 \times 5\)
  2. Group the fives: \(50 = 2 \times (5^2)\)
  3. Simplify: \(\sqrt{50} = 5\sqrt{2}\)
• Example 2: Simplify \(\sqrt{72}\)
  1. Prime factorization: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
  2. Group the factors: \(72 = (2^2) \times 2 \times (3^2)\)
  3. Simplify: \(\sqrt{72} = 6\sqrt{2}\)

By consistently applying these steps, you can simplify square roots effectively and accurately.

Simplifying the square root of 84 involves breaking it down into its prime factors and then simplifying the expression. Here is a detailed step-by-step guide to simplify √84:

1. Identify the Number: Start with the number you want to simplify, which is 84.
2. Prime Factorization: Break down 84 into its prime factors.
   • 84 is an even number, so it is divisible by 2: \(84 \div 2 = 42\)
   • 42 is also even, so divide by 2: \(42 \div 2 = 21\)
   • 21 is divisible by 3: \(21 \div 3 = 7\)
   • 7 is a prime number.

   Thus, the prime factorization of 84 is:

   $84=2\times 2\times 3\times 7$
3. Group the Factors: Pair the prime factors into groups of two.

   From the prime factorization \(2 \times 2 \times 3 \times 7\), we can group the twos together.

4. Simplify the Square Root: Take one factor from each pair outside the square root.

   The pair of twos (2²) can be taken out as a single 2:

   $\sqrt{2²\times 3\times 7}=2\times \sqrt{3\times 7}$
5. Combine the Factors: Multiply the factors outside the square root and simplify the remaining expression.

   The simplified form of the square root of 84 is:

   $2\surd 21$

Thus, the step-by-step simplification of the square root of 84 yields \(2\sqrt{21}\). This method ensures that the square root is in its simplest form, making it easier to work with in mathematical calculations.

To simplify the square root of 84, we can use the factor tree method. This method involves breaking down the number into its prime factors. Here is a step-by-step guide to using a factor tree for √84:

Step 1: Begin with the number 84 and divide it by the smallest prime number, which is 2.

1. 84 ÷ 2 = 42

Step 2: Continue dividing the quotient by the smallest prime number until you cannot divide evenly by that number.

1. 42 ÷ 2 = 21

Step 3: Now divide 21 by the next smallest prime number, which is 3.

1. 21 ÷ 3 = 7

Step 4: Since 7 is a prime number, we stop here.

The prime factors of 84 are 2, 2, 3, and 7. We can express this as:

84 = 2 × 2 × 3 × 7

Step 5: Group the prime factors into pairs of identical numbers.

• (2 × 2)
• (3 × 7)

Step 6: Take the square root of each pair. For every pair, take one number out of the square root.

√(2 × 2) × √(3 × 7) = 2 × √(3 × 7)

Step 7: Simplify the remaining expression under the square root.

√(3 × 7) = √21

Therefore, the simplified form of √84 is:

2√21

Using a factor tree helps us to systematically break down the number and simplify the square root. The final result is:

√84 = 2√21

The square root of 84 can be simplified using the prime factorization method. This involves breaking down 84 into its prime factors and then simplifying the square root based on these factors. Let's go through the process step by step.

Prime Factorization of 84

First, we need to find the prime factors of 84:

1. 84 is an even number, so it is divisible by 2:
• \(84 \div 2 = 42\)
2. 42 is also an even number, so we divide by 2 again:
• \(42 \div 2 = 21\)
3. 21 is divisible by 3 (since \(2 + 1 = 3\), which is divisible by 3):
• \(21 \div 3 = 7\)
4. 7 is a prime number.

So, the prime factorization of 84 is \(2 \times 2 \times 3 \times 7\) or \(2^2 \times 3 \times 7\).

Simplifying the Square Root

Now, we can use the prime factorization to simplify the square root:

\[\sqrt{84} = \sqrt{2^2 \times 3 \times 7}\]

We can take the square root of the perfect square (2²) out of the radical:

\[\sqrt{2^2 \times 3 \times 7} = 2 \times \sqrt{3 \times 7}\]

Simplify inside the radical:

\[\sqrt{3 \times 7} = \sqrt{21}\]

So the simplified form is:

\[\sqrt{84} = 2\sqrt{21}\]

Step-by-Step Breakdown

1. Factor 84 into its prime components: \(84 = 2^2 \times 3 \times 7\).
2. Identify and separate the perfect square factor: \(2^2\).
3. Rewrite the square root as a product of the square root of the perfect square and the remaining factors: \(\sqrt{84} = \sqrt{2^2 \times 21}\).
4. Simplify the square root of the perfect square: \(\sqrt{2^2} = 2\).
5. Combine the simplified square root with the remaining factors: \(2\sqrt{21}\).

Verification

To verify, we can square our result to check if it equals 84:

\[(2\sqrt{21})^2 = 2^2 \times (\sqrt{21})^2 = 4 \times 21 = 84\]

This confirms that our simplification is correct.

Visualizing the simplification of the square root of 84 can help in understanding the process better. Below, we will use a factor tree and a number line to illustrate the steps and the final simplified form.

Factor Tree Diagram

A factor tree breaks down 84 into its prime factors:

• Start with 84 at the top.
• Divide 84 by 2 (since 84 is even) to get 42.
• Divide 42 by 2 (since 42 is even) to get 21.
• Divide 21 by 3 to get 7.
• Since 7 is a prime number, the factorization ends here.

So, the prime factors of 84 are \(2 \times 2 \times 3 \times 7\).

Number Line Representation

On a number line, we can approximate the value of \(\sqrt{84}\) and compare it to its simplified form \(2\sqrt{21}\).

• \(\sqrt{84}\) is approximately 9.165 (since \(9^2 = 81\) and \(10^2 = 100\), \(\sqrt{84}\) lies between 9 and 10).
• \(2\sqrt{21}\) is also approximately 9.165 (since \(\sqrt{21} \approx 4.583\) and \(2 \times 4.583 = 9.166\)).

Visual Simplification Steps

We can visually break down the simplification steps:

1. Start with \(\sqrt{84}\).
2. Factorize 84: \(84 = 2^2 \times 3 \times 7\).
3. Separate the perfect square: \(\sqrt{2^2 \times 21} = \sqrt{2^2} \times \sqrt{21}\).
4. Simplify the perfect square: \(\sqrt{2^2} = 2\).
5. Combine the results: \(2\sqrt{21}\).

Graphical Representation

Using a graph, we can compare \(\sqrt{84}\) and \(2\sqrt{21}\) to show they are equal:

The graph shows that both expressions intersect at the same points, confirming that \(\sqrt{84} = 2\sqrt{21}\).

When simplifying the square root of 84, several common mistakes can occur. Being aware of these pitfalls can help ensure the correct simplification process. Here are some common mistakes and tips to avoid them:

Mistake 1: Incorrect Prime Factorization

One of the most common mistakes is not correctly identifying the prime factors of 84. To avoid this:

1. Ensure you start with the smallest prime number (2) and continue dividing until all factors are prime.
2. Double-check your factorization steps. The correct prime factorization of 84 is \(2^2 \times 3 \times 7\).

Mistake 2: Forgetting to Simplify Perfect Squares

Another mistake is not recognizing and simplifying perfect squares within the factorization:

1. Identify any perfect squares in the factorization. In the case of 84, \(2^2\) is a perfect square.
2. Extract the square root of the perfect square and place it outside the radical. For \(\sqrt{2^2 \times 21}\), simplify \(\sqrt{2^2}\) to 2, resulting in \(2\sqrt{21}\).

Mistake 3: Incorrectly Combining Factors

Combining factors incorrectly after simplification can lead to errors:

1. Ensure that only the square root of the non-perfect square factors remains under the radical.
2. For \(\sqrt{84}\), after extracting the 2 from \(\sqrt{2^2}\), make sure the remaining factors \(3 \times 7\) combine correctly as \(\sqrt{21}\).

Mistake 4: Arithmetic Errors

Basic arithmetic mistakes can disrupt the simplification process:

1. Carefully perform each division when factorizing the number.
2. Double-check each multiplication and division to ensure accuracy.

Tips for Avoiding Mistakes

• Double-check your work: Always rework your factorization and simplification steps to catch any errors.
• Practice regularly: Frequent practice with different numbers will help reinforce the correct process.
• Use tools: Utilize factor trees and other visual aids to help with the factorization process.
• Stay organized: Write down each step clearly to avoid confusion.

By being mindful of these common mistakes and following these tips, you can confidently simplify the square root of 84 and other numbers.

Simplified square roots have numerous applications across different fields, including mathematics, science, engineering, and everyday life. Understanding how to simplify square roots can make complex calculations easier and more intuitive. Here are some common applications:

• Geometry and Trigonometry

  Simplified square roots are frequently used in geometry and trigonometry to calculate distances, areas, and angles. For example, the Pythagorean theorem often involves square roots. Simplifying these roots can make it easier to solve problems.

  Example: Calculating the hypotenuse of a right triangle:

  If the legs of the triangle are 7 and 3√2, then the hypotenuse \( c \) is:

  \( c = \sqrt{7^2 + (3\sqrt{2})^2} = \sqrt{49 + 18} = \sqrt{67} \)

• Algebra

  Simplified square roots appear in algebraic equations, particularly in quadratic equations. Simplifying the square roots of discriminants can help solve these equations more efficiently.

  Example: Solving a quadratic equation:

  The quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) often requires simplifying the square root.

  For \( ax^2 + bx + c = 0 \) with \( a=1, b=6, c=9 \):

  \( x = \frac{-6 \pm \sqrt{6^2 - 4(1)(9)}}{2(1)} = \frac{-6 \pm \sqrt{36 - 36}}{2} = \frac{-6 \pm 0}{2} = -3 \)

• Physics

  In physics, simplified square roots are used to solve problems involving motion, force, and energy. They are particularly useful in simplifying the results of equations derived from physical laws.

  Example: Calculating the period of a pendulum:

  The period \( T \) of a simple pendulum is given by:

  \( T = 2\pi \sqrt{\frac{L}{g}} \)

  If \( L = 2 \) meters and \( g = 9.8 \, \text{m/s}^2 \), then:

  \( T = 2\pi \sqrt{\frac{2}{9.8}} = 2\pi \sqrt{0.204} \approx 2\pi (0.451) \approx 2.83 \) seconds

• Engineering

  Engineers often simplify square roots when designing structures, analyzing signals, and working with electrical circuits. Simplification can make calculations more manageable and results easier to interpret.

  Example: Analyzing electrical resistance:

  In AC circuits, impedance \( Z \) can be calculated using the formula:

  \( Z = \sqrt{R^2 + (X_L - X_C)^2} \)

  If \( R = 4 \, \Omega \), \( X_L = 3 \, \Omega \), and \( X_C = 1 \, \Omega \), then:

  \( Z = \sqrt{4^2 + (3 - 1)^2} = \sqrt{16 + 4} = \sqrt{20} = 2\sqrt{5} \, \Omega \)

• Everyday Life

  Understanding simplified square roots can be useful in various everyday situations, such as cooking, carpentry, and home improvement projects. It helps in making accurate measurements and calculations.

  Example: Calculating the diagonal of a TV screen:

  If a TV screen measures 48 inches by 27 inches, the diagonal \( d \) is:

  \( d = \sqrt{48^2 + 27^2} = \sqrt{2304 + 729} = \sqrt{3033} \approx 55 \) inches

To further understand how to simplify square roots, let's look at a few additional examples. We'll use the prime factorization method and show the step-by-step process for each example.

Example 1: Simplifying √50

1. Factorize 50 into its prime factors: \( 50 = 2 \times 5^2 \).
2. Group the factors into pairs: \( 50 = (5^2) \times 2 \).
3. Take the square root of each group: \( \sqrt{50} = \sqrt{5^2} \times \sqrt{2} = 5\sqrt{2} \).

Thus, the simplified form of \( \sqrt{50} \) is \( 5\sqrt{2} \).

Example 2: Simplifying √72

1. Factorize 72 into its prime factors: \( 72 = 2^3 \times 3^2 \).
2. Group the factors into pairs: \( 72 = (2^2) \times 2 \times (3^2) \).
3. Take the square root of each group: \( \sqrt{72} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2} = 2 \times 3 \times \sqrt{2} \).
4. Multiply the results: \( 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).

Thus, the simplified form of \( \sqrt{72} \) is \( 6\sqrt{2} \).

Example 3: Simplifying √98

1. Factorize 98 into its prime factors: \( 98 = 2 \times 7^2 \).
2. Group the factors into pairs: \( 98 = (7^2) \times 2 \).
3. Take the square root of each group: \( \sqrt{98} = \sqrt{7^2} \times \sqrt{2} = 7\sqrt{2} \).

Thus, the simplified form of \( \sqrt{98} \) is \( 7\sqrt{2} \).

Example 4: Simplifying √200

1. Factorize 200 into its prime factors: \( 200 = 2^3 \times 5^2 \).
2. Group the factors into pairs: \( 200 = (2^2) \times 2 \times (5^2) \).
3. Take the square root of each group: \( \sqrt{200} = \sqrt{2^2} \times \sqrt{5^2} \times \sqrt{2} = 2 \times 5 \times \sqrt{2} \).
4. Multiply the results: \( 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \).

Thus, the simplified form of \( \sqrt{200} \) is \( 10\sqrt{2} \).

Example 5: Simplifying √180

1. Factorize 180 into its prime factors: \( 180 = 2^2 \times 3^2 \times 5 \).
2. Group the factors into pairs: \( 180 = (2^2) \times (3^2) \times 5 \).
3. Take the square root of each group: \( \sqrt{180} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{5} = 2 \times 3 \times \sqrt{5} \).
4. Multiply the results: \( 2 \times 3 \times \sqrt{5} = 6\sqrt{5} \).

Thus, the simplified form of \( \sqrt{180} \) is \( 6\sqrt{5} \).

Practicing with square roots is essential for mastering the concepts. Below are several practice problems to help you understand the simplification process and applications of square roots.

1. Simplify the following square roots:

   • \(\sqrt{50}\)
   • \(\sqrt{75}\)
   • \(\sqrt{200}\)

   Solutions:

   • \(\sqrt{50} = 5\sqrt{2}\)
   • \(\sqrt{75} = 5\sqrt{3}\)
   • \(\sqrt{200} = 10\sqrt{2}\)

2. Express each of the following square roots in its simplest radical form:

   • \(\sqrt{32}\)
   • \(\sqrt{48}\)
   • \(\sqrt{180}\)

   Solutions:

   • \(\sqrt{32} = 4\sqrt{2}\)
   • \(\sqrt{48} = 4\sqrt{3}\)
   • \(\sqrt{180} = 6\sqrt{5}\)

3. Use the prime factorization method to simplify:

   • \(\sqrt{72}\)
   • \(\sqrt{98}\)

   Solutions:

   • \(\sqrt{72} = 6\sqrt{2}\)
   • \(\sqrt{98} = 7\sqrt{2}\)

4. Find the square root and round to the nearest hundredth:

   • \(\sqrt{84}\)
   • \(\sqrt{150}\)

   Solutions:

   • \(\sqrt{84} \approx 9.17\)
   • \(\sqrt{150} \approx 12.25\)

5. Solve the following word problem:

   Mary wants to create a square garden with an area of 84 square feet. To the nearest tenth, what will be the length of each side of the garden?

   Solution:

   \(\sqrt{84} \approx 9.2\) feet

These problems will help reinforce your understanding of simplifying square roots and applying them in different contexts.

Understanding the simplification of the square root of 84 provides a solid foundation for handling more complex mathematical problems. By simplifying √84 to 2√21, we leverage fundamental concepts of prime factorization and the properties of square roots, which are applicable across various mathematical disciplines.

Here are the key takeaways:

• The square root of 84 is an irrational number, approximately equal to 9.165 when expressed in decimal form.
• Using prime factorization, we can express 84 as \(2^2 \times 21\). This allows us to simplify √84 to 2√21.
• Simplified square roots, like 2√21, are useful in many mathematical applications, including geometry, algebra, and calculus.
• Practicing the simplification process with various numbers enhances your problem-solving skills and mathematical understanding.

Simplifying square roots helps in solving equations more efficiently and provides a clearer understanding of mathematical relationships. This foundational skill is crucial for progressing to more advanced topics in mathematics.

We encourage continued practice with different numbers and exploring their applications to solidify your understanding of these concepts. By mastering the simplification of square roots, you can tackle a wide range of mathematical challenges with confidence.

Below are some common questions regarding the simplification of the square root of 84:

• What is the simplified form of the square root of 84?

  The simplified form of the square root of 84 is \(2\sqrt{21}\).

• How do you simplify the square root of 84?

  To simplify the square root of 84:

  1. Find the prime factors of 84: \(84 = 2^2 \times 21\).
  2. Separate the perfect square factor: \(\sqrt{84} = \sqrt{2^2 \times 21}\).
  3. Take the square root of the perfect square: \(\sqrt{2^2} = 2\).
  4. Combine the simplified square root: \(\sqrt{84} = 2\sqrt{21}\).
• Why is it important to simplify square roots?

  Simplifying square roots makes them easier to understand and work with in further mathematical calculations. It also helps in recognizing the properties of numbers more clearly.

• Can all square roots be simplified?

  No, not all square roots can be simplified to a simpler radical form. A square root can only be simplified if the radicand (the number under the square root) has a perfect square factor.

• What are the practical applications of simplified square roots?

  Simplified square roots are used in various fields such as engineering, physics, and computer science, where precise calculations are necessary. They are also essential in solving quadratic equations, working with trigonometric functions, and optimizing algorithms.

• What tools can help in simplifying square roots?

  Several online tools and calculators can assist in simplifying square roots, such as Symbolab, Mathway, and Microsoft Math Solver. These tools provide step-by-step solutions and explanations.