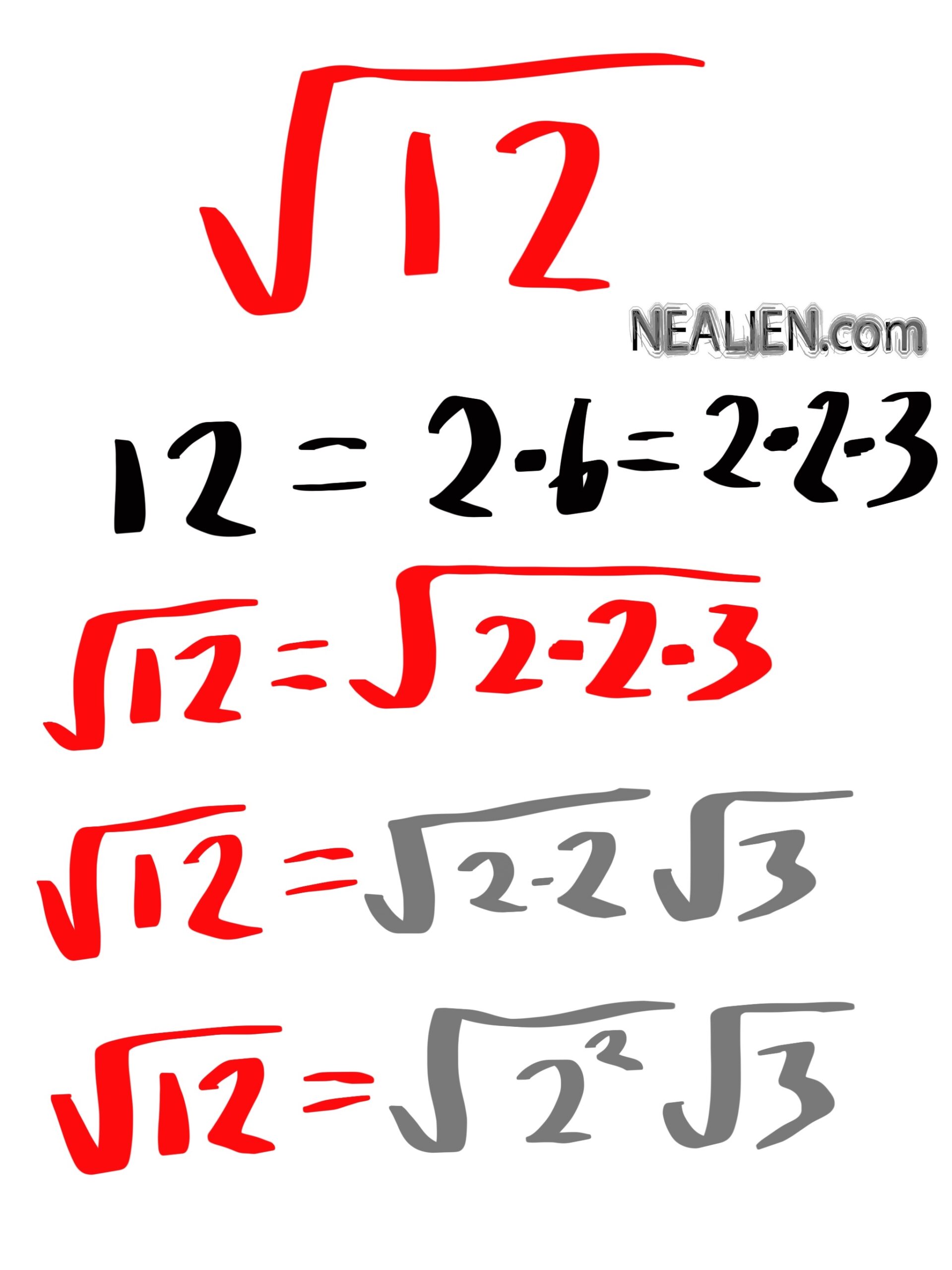Topic square roots simplified calculator: Discover the simplicity and efficiency of our Square Roots Simplified Calculator. This comprehensive guide provides step-by-step instructions and valuable insights to help you effortlessly simplify square roots. Perfect for students, educators, and math enthusiasts, our tool and tips make understanding square roots easier than ever. Start simplifying today and master square roots with confidence!
Table of Content
- Square Roots Simplified Calculator
- Introduction to Square Roots
- What is a Square Root?
- Importance of Simplifying Square Roots
- Basic Steps to Simplify Square Roots
- Common Methods for Simplifying Square Roots
- Using a Square Roots Simplified Calculator
- Benefits of Using a Square Roots Calculator
- Step-by-Step Guide to Simplifying Square Roots
- Examples of Simplified Square Roots
- Square Roots of Perfect Squares
- Square Roots of Non-Perfect Squares
- Frequently Asked Questions (FAQs)
- Troubleshooting Common Issues
- Advanced Techniques for Simplifying Square Roots
- Mathematical Background and Theory
- Applications of Simplified Square Roots
- Conclusion and Final Thoughts
- YOUTUBE: Xem video hướng dẫn sử dụng máy tính ClassWiz để đơn giản hóa căn bậc hai một cách hiệu quả. Phù hợp cho những ai đang tìm kiếm thông tin về 'square roots simplified calculator'.
Square Roots Simplified Calculator
Welcome to the Square Roots Simplified Calculator. This tool helps you simplify square roots quickly and accurately. Below you will find information on how to use the calculator and examples to guide you through the process.
How to Use the Calculator
- Enter the number you want to simplify the square root for in the input field.
- Click on the "Simplify" button.
- The calculator will display the simplified square root.
Examples
-
Example 1: Simplifying \(\sqrt{50}\)
\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\] -
Example 2: Simplifying \(\sqrt{72}\)
\[
\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}
\] -
Example 3: Simplifying \(\sqrt{98}\)
\[
\sqrt{98} = \sqrt{49 \times 2} = \sqrt{49} \times \sqrt{2} = 7\sqrt{2}
\]
Calculator
Enter the number to simplify its square root:

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics and is widely used across various fields. Understanding square roots is essential for simplifying complex equations, solving mathematical problems, and applying mathematical principles in real-life scenarios.
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, since 5 multiplied by 5 equals 25. Mathematically, this is represented as:
\(\sqrt{25} = 5\)
Square roots can be categorized into two main types:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25, which have whole numbers as their square roots.
- Non-Perfect Squares: Numbers like 2, 3, 5, and 10, which do not have whole numbers as their square roots and are typically expressed in decimal or simplified radical forms.
The importance of square roots lies in their applications, including geometry, algebra, and real-world problem-solving. For instance, calculating the area of a square, determining distances, and solving quadratic equations often require the use of square roots.
To simplify a square root, follow these basic steps:
- Factorize the number: Break down the number inside the square root into its prime factors.
- Identify perfect squares: Look for pairs of prime factors that can form perfect squares.
- Simplify: For each pair of prime factors, take one factor out of the square root.
For example, to simplify \(\sqrt{18}\):
- Factorize 18 into \(2 \times 3 \times 3\).
- Identify the pair of 3s, which form a perfect square (\(3^2\)).
- Simplify by taking 3 out of the square root: \(\sqrt{18} = 3\sqrt{2}\).
Using a square root calculator can significantly simplify these steps, providing quick and accurate results. These calculators not only compute the square roots but also help in simplifying radical expressions and handling both perfect and non-perfect squares.
In summary, mastering square roots and their simplifications is crucial for anyone dealing with mathematical computations. Whether you are a student, engineer, or math enthusiast, understanding the principles of square roots will enhance your problem-solving skills and mathematical knowledge.
What is a Square Root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because \(3 \times 3 = 9\). This can be expressed mathematically as:
\[\sqrt{9} = 3\]
Every positive real number has two square roots: one positive and one negative. Thus, for 9, both 3 and -3 are square roots since:
\[3^2 = 9 \quad \text{and} \quad (-3)^2 = 9\]
The principal square root is the non-negative root, so when we refer to "the square root" of a positive number, we typically mean the principal square root.
The symbol for the square root is \(\sqrt{}\), called the radical sign, and the number inside the radical sign is called the radicand.
- If \(x\) is a non-negative real number, \(\sqrt{x}\) denotes the principal square root of \(x\).
- If \(x\) is negative, the square root of \(x\) is a complex number. For example, \(\sqrt{-1} = i\), where \(i\) is the imaginary unit.
Square roots have several important properties, including:
- Multiplication: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Division: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Square of a square root: \((\sqrt{a})^2 = a\)
Understanding these properties helps in simplifying expressions involving square roots and solving equations.
For example:
\[\sqrt{16} = 4\], because \(4^2 = 16\).
\[\sqrt{25} = 5\], because \(5^2 = 25\).
When dealing with non-perfect squares, the square root is often expressed in its simplest radical form or as a decimal approximation. For example:
\[\sqrt{20} = 2\sqrt{5} \approx 4.472\]
Square roots are essential in various fields such as algebra, geometry, and calculus. They are used in solving quadratic equations, finding distances, and in many mathematical proofs and applications.
Importance of Simplifying Square Roots
Simplifying square roots is a crucial mathematical skill that has several important benefits. Understanding the significance of this process can help students and enthusiasts appreciate its application in various mathematical contexts. Below are some key reasons why simplifying square roots is important:
-
Enhances Mathematical Understanding:
Simplifying square roots helps in grasping the concept of prime factorization and properties of numbers. It enables a deeper understanding of how numbers are constructed and interrelated.
-
Simplifies Complex Calculations:
By breaking down square roots into their simplest forms, it becomes easier to handle and solve more complex mathematical problems. This is particularly useful in algebra, calculus, and geometry.
-
Improves Accuracy:
Simplifying square roots reduces the likelihood of errors in calculations. Working with simpler, reduced forms of square roots minimizes the risk of mistakes that can occur with larger, more complicated numbers.
-
Facilitates Comparison:
Simplified square roots make it easier to compare and contrast different roots. For example, comparing \( \sqrt{50} \) and \( \sqrt{75} \) is simpler when they are reduced to \( 5\sqrt{2} \) and \( 5\sqrt{3} \), respectively.
-
Essential for Further Studies:
Simplifying square roots is a foundational skill that is essential for advanced mathematical studies. Topics such as quadratic equations, trigonometry, and complex numbers often require proficiency in working with square roots.
-
Real-world Applications:
Simplified square roots are used in various real-world applications, including engineering, physics, and computer science. For example, in calculating distances, areas, and volumes, having a simplified form can make practical computations more efficient.
Basic Steps to Simplify Square Roots
To simplify square roots, follow these basic steps:
- Identify Perfect Squares: Determine if the number under the square root can be broken down into smaller perfect square factors (such as 4, 9, 16, 25, etc.).
- Factorize the Number: Write the number inside the square root as a product of its prime factors.
- Separate the Perfect Squares: Split the square root into two separate roots, where one contains the perfect square factors and the other contains the remaining factors.
- Simplify the Perfect Squares: Take the square root of the perfect square factors. These come out of the square root as integers.
- Multiply the Results: Multiply the integers obtained from the perfect squares with the remaining square root.
Here's a step-by-step example to illustrate the process:
Example: Simplify \( \sqrt{72} \)
- Identify Perfect Squares: The number 72 can be factored into 36 and 2, where 36 is a perfect square.
- Factorize the Number: \( 72 = 36 \times 2 \)
- Separate the Perfect Squares: \( \sqrt{72} = \sqrt{36 \times 2} \)
- Simplify the Perfect Squares: \( \sqrt{36} = 6 \)
- Multiply the Results: \( 6 \sqrt{2} \)
Therefore, \( \sqrt{72} \) simplifies to \( 6 \sqrt{2} \).

Common Methods for Simplifying Square Roots
Simplifying square roots involves reducing the expression inside the square root to its simplest form. Here are some common methods to achieve this:
-
Prime Factorization:
Find the prime factors of the number inside the square root. Pair the prime factors, and for each pair, take one number out of the square root.
- Example: \( \sqrt{72} \)
- Prime factorization of 72: \( 72 = 2^3 \times 3^2 \)
- Pairs: \( (2 \times 2) \) and \( 3 \times 3 \)
- Simplified form: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 6\sqrt{2} \)
-
Extracting Square Factors:
Identify and extract the largest perfect square factor from the radicand (the number inside the square root).
- Example: \( \sqrt{50} \)
- Largest perfect square factor of 50: 25
- Simplified form: \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \)
-
Using Properties of Radicals:
Apply the properties of radicals to simplify expressions. These properties include:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- Example: \( \sqrt{18 \times 2} = \sqrt{18} \times \sqrt{2} = 3\sqrt{2} \times \sqrt{2} = 6 \)
- Example: \( \sqrt{\frac{16}{9}} = \frac{\sqrt{16}}{\sqrt{9}} = \frac{4}{3} \)
These methods can be used individually or in combination to simplify square roots efficiently. Practicing these techniques will help in quickly identifying and extracting square factors, making the process of simplification much easier.
Using a Square Roots Simplified Calculator
Using a square roots simplified calculator is an efficient way to simplify square roots and obtain results quickly and accurately. Here’s a step-by-step guide on how to use such a calculator:
-
Enter the Number: Start by entering the number for which you want to find the square root into the input field of the calculator. This number is often referred to as the radicand.
- Example: Enter 27 to find the simplified form of √27.
-
Select the Calculation: Depending on the calculator, you may need to select the type of calculation you want to perform. Choose the option to "Calculate the Square Root" or "Simplify Square Root".
- Example: Select "Simplify" to get the simplest radical form.
-
Submit the Input: Click the "Calculate" or similar button to process the input. The calculator will then perform the necessary computations to simplify the square root.
- Example: Click "Calculate" after entering 27.
-
View the Results: The calculator will display the simplified form of the square root, often in both exact form and decimal form. This includes breaking down the radicand into its prime factors and extracting the square root of any perfect squares.
- Example: For √27, the calculator will show √27 = 3√3.
Using these calculators can simplify your work, especially when dealing with larger numbers or more complex expressions. They are particularly helpful for students, educators, and anyone needing quick and reliable calculations. Here are a few popular online square roots simplified calculators you can use:
Benefits of Using a Square Roots Calculator
Using a square roots calculator can provide numerous advantages, especially for students, educators, and professionals dealing with mathematical calculations. Here are some key benefits:
- Accuracy: A square roots calculator ensures precise calculations, minimizing the risk of human error, which is especially important in fields requiring high accuracy, such as engineering and physics.
- Time-Saving: Calculating square roots manually can be time-consuming. A calculator quickly provides results, saving valuable time for other tasks.
- Convenience: With a square roots calculator, you can easily simplify complex square root problems without needing to remember or apply various mathematical rules and formulas.
- Educational Tool: These calculators are excellent for learning and teaching purposes, helping students understand the process of simplifying square roots and verifying their manual calculations.
- Consistency: A calculator provides consistent results every time, which is crucial for standardized tests and repeated calculations in scientific research.
- Accessibility: Many square roots calculators are available online for free, making them easily accessible from any device with an internet connection.
- Advanced Functions: Some calculators offer additional features, such as handling variables, complex numbers, and detailed step-by-step solutions, enhancing their utility for advanced mathematics.
- Visualization: Certain calculators provide graphical representations of square roots, aiding in the visual understanding of the mathematical concepts involved.
Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest radical form. Follow these steps to simplify square roots efficiently:
-
Identify the factors:
Find the factors of the number under the square root. Look for perfect square factors (e.g., 4, 9, 16, 25) because they simplify nicely.
-
Rewrite the square root:
Express the number as a product of two factors, where one factor is a perfect square. For example, to simplify √45, notice that 45 = 9 × 5.
-
Apply the square root property:
Use the property √(a × b) = √a × √b. For √45, this becomes √(9 × 5) = √9 × √5.
-
Simplify the square root of the perfect square:
Since √9 is 3, we simplify √45 to 3√5.
Here are a few more examples:
- Example 1: Simplify √27
Identify factors: 27 = 9 × 3
Rewrite: √27 = √(9 × 3)
Apply property: √27 = √9 × √3 = 3√3
- Example 2: Simplify √8
Identify factors: 8 = 4 × 2
Rewrite: √8 = √(4 × 2)
Apply property: √8 = √4 × √2 = 2√2
- Example 3: Simplify √144
Identify factors: 144 = 12 × 12 (144 is a perfect square)
Simplify directly: √144 = 12
Remember, the key to simplifying square roots is to break down the number into factors and look for perfect squares. Practice these steps to become proficient in simplifying square roots.

Examples of Simplified Square Roots
Here are some common examples of how to simplify square roots using basic principles and methods:
Example 1: Simplifying √12
First, identify the factors of 12. Notice that 12 can be factored into 4 and 3, where 4 is a perfect square.
√12 = √(4 × 3) = √4 × √3 = 2√3
So, √12 simplifies to 2√3.
Example 2: Simplifying √18
Factor 18 into 9 and 2, where 9 is a perfect square.
√18 = √(9 × 2) = √9 × √2 = 3√2
So, √18 simplifies to 3√2.
Example 3: Simplifying √45
Factor 45 into 9 and 5, where 9 is a perfect square.
√45 = √(9 × 5) = √9 × √5 = 3√5
So, √45 simplifies to 3√5.
Example 4: Simplifying √50
Factor 50 into 25 and 2, where 25 is a perfect square.
√50 = √(25 × 2) = √25 × √2 = 5√2
So, √50 simplifies to 5√2.
Example 5: Simplifying √72
Factor 72 into 36 and 2, where 36 is a perfect square.
√72 = √(36 × 2) = √36 × √2 = 6√2
So, √72 simplifies to 6√2.
Example 6: Simplifying √200
Factor 200 into 100 and 2, where 100 is a perfect square.
√200 = √(100 × 2) = √100 × √2 = 10√2
So, √200 simplifies to 10√2.
Example 7: Simplifying √32
Factor 32 into 16 and 2, where 16 is a perfect square.
√32 = √(16 × 2) = √16 × √2 = 4√2
So, √32 simplifies to 4√2.
Example 8: Simplifying √75
Factor 75 into 25 and 3, where 25 is a perfect square.
√75 = √(25 × 3) = √25 × √3 = 5√3
So, √75 simplifies to 5√3.
Example 9: Simplifying √128
Factor 128 into 64 and 2, where 64 is a perfect square.
√128 = √(64 × 2) = √64 × √2 = 8√2
So, √128 simplifies to 8√2.
Example 10: Simplifying √20
Factor 20 into 4 and 5, where 4 is a perfect square.
√20 = √(4 × 5) = √4 × √5 = 2√5
So, √20 simplifies to 2√5.
Example 11: Simplifying √27
Factor 27 into 9 and 3, where 9 is a perfect square.
√27 = √(9 × 3) = √9 × √3 = 3√3
So, √27 simplifies to 3√3.
Example 12: Simplifying √80
Factor 80 into 16 and 5, where 16 is a perfect square.
√80 = √(16 × 5) = √16 × √5 = 4√5
So, √80 simplifies to 4√5.
Square Roots of Perfect Squares
Perfect squares are numbers that are the square of an integer. The square root of a perfect square is always an integer. Here are some examples of perfect squares and their square roots:
| Perfect Square | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 4 | \(\sqrt{4} = 2\) |
| 9 | \(\sqrt{9} = 3\) |
| 16 | \(\sqrt{16} = 4\) |
| 25 | \(\sqrt{25} = 5\) |
| 36 | \(\sqrt{36} = 6\) |
| 49 | \(\sqrt{49} = 7\) |
| 64 | \(\sqrt{64} = 8\) |
| 81 | \(\sqrt{81} = 9\) |
| 100 | \(\sqrt{100} = 10\) |
Here are some additional examples of perfect squares and their square roots for larger numbers:
- \(\sqrt{121} = 11\)
- \(\sqrt{144} = 12\)
- \(\sqrt{169} = 13\)
- \(\sqrt{196} = 14\)
- \(\sqrt{225} = 15\)
- \(\sqrt{256} = 16\)
- \(\sqrt{289} = 17\)
- \(\sqrt{324} = 18\)
- \(\sqrt{361} = 19\)
- \(\sqrt{400} = 20\)
To determine if a number is a perfect square, you can take its square root and check if the result is an integer. For instance, the number 81 has a square root of 9, which is an integer, thus 81 is a perfect square. On the other hand, the number 50 has a square root of approximately 7.07, which is not an integer, thus 50 is not a perfect square.
Perfect squares are commonly used in algebra and geometry to simplify expressions and solve equations. Understanding perfect squares and their properties can be extremely helpful in various mathematical applications.
Square Roots of Non-Perfect Squares
Square roots of non-perfect squares can be challenging to simplify because they do not result in whole numbers. However, with a systematic approach, we can simplify these square roots into their simplest radical form. Here are the steps to simplify square roots of non-perfect squares:
- Identify the prime factors of the number under the square root.
- Pair the prime factors in groups of two.
- Move one number from each pair outside the square root.
- Multiply the numbers outside the square root together.
- Keep the remaining numbers inside the square root and multiply them.
Let's go through an example to illustrate these steps:
Example: Simplify \( \sqrt{72} \)
- Find the prime factors of 72:
- 72 = 2 × 2 × 2 × 3 × 3
- Group the prime factors in pairs:
- (2 × 2), (3 × 3), 2
- Move one number from each pair outside the square root:
- 2 and 3 move outside the square root
- Multiply the numbers outside the square root together:
- 2 × 3 = 6
- Keep the remaining number inside the square root:
- \( \sqrt{2} \)
So, \( \sqrt{72} = 6\sqrt{2} \).
For more practice, let's look at another example:
Example: Simplify \( \sqrt{50} \)
- Find the prime factors of 50:
- 50 = 2 × 5 × 5
- Group the prime factors in pairs:
- (5 × 5), 2
- Move one number from each pair outside the square root:
- 5 moves outside the square root
- Multiply the numbers outside the square root together:
- 5
- Keep the remaining number inside the square root:
- \( \sqrt{2} \)
So, \( \sqrt{50} = 5\sqrt{2} \).
By following these steps, you can simplify square roots of any non-perfect square.
Frequently Asked Questions (FAQs)
-
What is a square root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \( 5 \times 5 = 25 \).
-
How do you simplify square roots?
To simplify a square root, find the prime factors of the number and pair the identical factors. For example, to simplify \( \sqrt{72} \):
- Find the prime factors of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Pair the identical factors: \( (2 \times 2) \times (3 \times 3) \times 2 \)
- Take one factor from each pair: \( 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
-
What is a perfect square?
A perfect square is a number that has an integer as its square root. Examples include 1, 4, 9, 16, 25, etc. For instance, the square root of 16 is 4 because \( 4 \times 4 = 16 \).
-
Can all square roots be simplified?
No, not all square roots can be simplified. Only square roots of perfect squares or numbers that can be factored into perfect squares can be simplified. For example, \( \sqrt{20} \) can be simplified to \( 2\sqrt{5} \), but \( \sqrt{7} \) cannot be simplified further.
-
How does a Square Roots Simplified Calculator work?
A Square Roots Simplified Calculator automatically finds the prime factors of a number, pairs them, and simplifies the square root. It provides quick and accurate results, saving time and effort.
-
What are the benefits of using a Square Roots Simplified Calculator?
Using a calculator simplifies the process, reduces errors, and helps in learning and verifying the simplification steps. It is especially useful for large numbers and complex calculations.
-
Can I use a Square Roots Simplified Calculator for any number?
Yes, a Square Roots Simplified Calculator can be used for any positive number. However, it cannot simplify square roots of negative numbers as they involve imaginary numbers.
-
Are there any limitations to these calculators?
While they are highly efficient, they are limited to simplifying real numbers. They cannot handle complex or imaginary numbers directly.
-
Do I need to understand the math behind it to use the calculator?
No, you don't need to understand the math behind it to use the calculator. However, understanding the steps can help in learning and verifying the results manually.
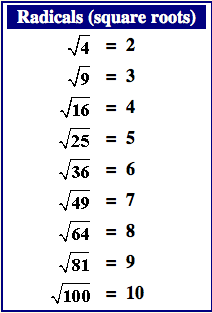
Troubleshooting Common Issues
When using a square roots simplified calculator, you might encounter a few common issues. Here’s a guide to help you troubleshoot and resolve them:
- Incorrect Input Format:
Ensure that you are entering numbers correctly. The calculator may not accept letters or special characters. If you need to input a square root, use the correct syntax (e.g., √25).
- Check that you are using numerical digits only.
- Avoid using commas, periods, or other non-numeric characters.
- If entering a square root directly, use a proper format such as √ followed by the number.
- Calculator Not Responding:
If the calculator is not responding or showing results:
- Ensure your internet connection is stable.
- Refresh the web page to reload the calculator.
- Clear your browser cache and cookies, then try again.
- Try accessing the calculator using a different browser or device.
- Inaccurate Results:
Sometimes, the results may not be accurate. Follow these steps to verify:
- Double-check your input for any mistakes.
- Recalculate manually to verify the result.
- Use another reliable calculator for comparison.
- Understanding Complex Results:
If the simplified square root results are complex (involving imaginary numbers), consider the following:
- Review the mathematical principles behind complex numbers and imaginary units.
- Ensure that the input value is suitable for real number simplification.
- Consult additional resources or a math expert if needed.
- Mathematical Errors:
If you suspect a mathematical error in the simplification process:
- Review the steps provided by the calculator for each simplification.
- Ensure you understand the properties of square roots and their simplification methods.
- Cross-check with algebraic rules and principles to confirm the correctness.
- Technical Glitches:
In case of any technical glitches with the calculator:
- Report the issue to the website or tool developer.
- Look for updates or patches that might resolve the issue.
- Try using the calculator at a different time if server issues are suspected.
By following these steps, you can effectively troubleshoot common issues encountered when using a square roots simplified calculator. If problems persist, consider reaching out for professional support or using alternative mathematical tools.
Advanced Techniques for Simplifying Square Roots
Simplifying square roots can sometimes involve advanced techniques, especially when dealing with more complex numbers. Here are some methods to help you simplify square roots more efficiently:
-
Prime Factorization:
Break down the number under the square root into its prime factors. For example, to simplify √72:
- Find the prime factors of 72: \(72 = 2^3 \times 3^2\).
- Group the prime factors into pairs: \(2^2 \times 3^2 \times 2\).
- Simplify using the pairs: \(√72 = √(2^2 \times 3^2 \times 2) = 2 \times 3 \times √2 = 6√2\).
-
Using Exponent Rules:
Apply the properties of exponents to simplify the square root. For instance:
\(√(a \times b) = √a \times √b\).
Example: \(√50 = √(25 \times 2) = √25 \times √2 = 5√2\).
-
Rationalizing the Denominator:
When the square root appears in the denominator, multiply the numerator and the denominator by a suitable value to rationalize it. For example, to simplify \( \frac{1}{√2} \):
- Multiply both the numerator and the denominator by \(√2\):
- \( \frac{1 \times √2}{√2 \times √2} = \frac{√2}{2}\).
-
Simplifying Higher Order Roots:
The process for simplifying cube roots or higher-order roots is similar to square roots but involves finding perfect cubes or higher powers. For example:
To simplify \( \sqrt[3]{192} \):
- Find the prime factors: \(192 = 64 \times 3 = 4^3 \times 3\).
- Simplify using the cube root: \( \sqrt[3]{192} = \sqrt[3]{64 \times 3} = \sqrt[3]{64} \times \sqrt[3]{3} = 4 \sqrt[3]{3}\).
-
Combining Like Terms:
When adding or subtracting square roots, combine like terms. For example:
\(3√2 + 2√2 = 5√2\).
-
Special Cases:
Recognize and simplify special cases involving perfect squares or other recognizable patterns.
Example: \(√(a^2 \times b) = a√b\).
These techniques will help you simplify square roots more effectively, whether you are dealing with simple or complex numbers. Practice regularly to become proficient in these methods.
Mathematical Background and Theory
Understanding the mathematical background and theory behind square roots is crucial for simplifying them effectively. Here, we will explore the key concepts and principles that form the foundation of square roots.
Definition of a Square Root
A square root of a number x is a number y such that y2 = x. For example, the square root of 9 is 3 because 32 = 9.
Properties of Square Roots
- Non-Negative Numbers: The square root of a non-negative number is always non-negative.
- Product Property: The square root of a product is equal to the product of the square roots: √(ab) = √a * √b.
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots: √(a/b) = √a / √b.
Rational and Irrational Numbers
Square roots can be either rational or irrational:
- Rational Square Roots: If the square root of a number is a fraction, it is rational. For example, √4 = 2.
- Irrational Square Roots: If the square root of a number is not a fraction, it is irrational. For example, √2 ≈ 1.414.
Simplifying Square Roots
The process of simplifying square roots involves expressing the square root in its simplest form. This can be achieved by factoring the number under the square root into its prime factors and then simplifying.
- Prime Factorization: Find the prime factors of the number under the square root.
- Group Factors: Group the prime factors into pairs.
- Simplify: Move the pairs outside the square root, as a single factor.
For example, to simplify √18:
- Prime factorize 18: 18 = 2 * 3 * 3
- Group the factors: √(2 * 3 * 3)
- Simplify: 3√2
Square Roots in the Real World
Square roots have numerous applications in various fields such as engineering, physics, and finance. They are used in calculations involving areas, volumes, and in solving quadratic equations.
Mathematical Notation with MathJax
Using MathJax, we can represent square roots and related mathematical concepts in a clear and precise manner. Here are some examples:
- Square root of x: \( \sqrt{x} \)
- Product property: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \)
- Quotient property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
Applications of Simplified Square Roots
Simplified square roots have numerous practical applications across various fields of mathematics, science, and everyday life. Understanding these applications can enhance problem-solving skills and provide a deeper appreciation of mathematical concepts. Here are some key applications:
Pythagorean Theorem
The Pythagorean theorem is a fundamental principle in geometry that relates the sides of a right-angled triangle. If the lengths of the two perpendicular sides are \( a \) and \( b \), and the length of the hypotenuse is \( c \), then:
\[ c^2 = a^2 + b^2 \]
Solving for the hypotenuse \( c \) involves finding the square root:
\[ c = \sqrt{a^2 + b^2} \]
This theorem is essential in fields such as architecture, engineering, and physics for calculating distances and designing structures.
Quadratic Equations
Quadratic equations, which are polynomial equations of degree 2, often involve square roots in their solutions. The general form of a quadratic equation is:
\[ ax^2 + bx + c = 0 \]
The solutions can be found using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Square roots are critical in solving these equations, which appear in various scientific and engineering problems.
Distance Formula
The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane can be calculated using the distance formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
This formula is widely used in fields such as navigation, robotics, and geography to determine the shortest path between points.
Vector Analysis
In vector mathematics, the magnitude of a vector \(\mathbf{v} = (v_1, v_2, v_3)\) is found using the square root of the sum of the squares of its components:
\[ |\mathbf{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2} \]
This application is crucial in physics and engineering for understanding forces and directions.
Financial Mathematics
Square roots are also used in financial calculations, such as determining the standard deviation in statistics, which measures the dispersion of a set of values. The formula involves the square root of the variance:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2} \]
Where \( \sigma \) is the standard deviation, \( N \) is the number of observations, \( x_i \) are the individual values, and \( \mu \) is the mean of the values. This is important for assessing risk in finance.
Signal Processing
In signal processing, square roots are used in algorithms to analyze and filter signals. For example, the root mean square (RMS) value of a signal is a measure of its effective power and is computed as:
\[ \text{RMS} = \sqrt{\frac{1}{N} \sum_{i=1}^N x_i^2} \]
This application is vital in electrical engineering and audio processing.
Complex Numbers
Square roots are used in the calculation of magnitudes of complex numbers. For a complex number \( z = a + bi \), its magnitude is given by:
\[ |z| = \sqrt{a^2 + b^2} \]
This is fundamental in various fields, including electronics and quantum mechanics.
Geometric Applications
Simplified square roots are also applied in calculating areas and volumes of geometric shapes. For example, the side length of a square given its area \( A \) is:
\[ s = \sqrt{A} \]
Similarly, for a cube with volume \( V \), the edge length is:
\[ e = \sqrt[3]{V} \]
These calculations are essential in construction, manufacturing, and design.
Understanding these applications highlights the importance of mastering square roots and their simplification. These concepts are integral to many scientific, engineering, and everyday calculations.
Conclusion and Final Thoughts
Simplifying square roots is an essential mathematical skill that has various applications in both academic and real-world scenarios. Throughout this guide, we have explored the definition of square roots, their importance, and the different methods for simplifying them. By using a square roots simplified calculator, we can easily and accurately simplify complex radical expressions, saving time and reducing errors.
The mathematical theory behind square roots is grounded in understanding the properties of numbers and their relationships. Simplifying square roots involves breaking down the radicand into its prime factors and then using properties of exponents and radicals to simplify the expression. This process not only helps in solving mathematical problems but also enhances our comprehension of algebraic principles.
Using a square roots calculator, such as the ones provided by CalculatorSoup, Mathway, and MathWarehouse, can be extremely beneficial. These tools allow for quick calculations, providing both exact and approximate values for square roots. They are particularly useful for students and professionals who need to perform frequent and accurate calculations.
In conclusion, mastering the simplification of square roots is a valuable skill that aids in the understanding of more complex mathematical concepts. By leveraging technology, such as online calculators, we can streamline our work and focus on applying these principles in various fields, from engineering to finance. As you continue to explore the world of mathematics, remember that tools and resources are available to support your learning and problem-solving endeavors.
We hope this comprehensive guide has provided you with the knowledge and confidence to simplify square roots effectively. Keep practicing, and don't hesitate to use the available calculators to enhance your learning experience. Thank you for reading, and we wish you success in all your mathematical pursuits.
Xem video hướng dẫn sử dụng máy tính ClassWiz để đơn giản hóa căn bậc hai một cách hiệu quả. Phù hợp cho những ai đang tìm kiếm thông tin về 'square roots simplified calculator'.
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Xem video hướng dẫn đơn giản hóa căn bậc hai bằng máy tính đồ thị. Phù hợp cho những ai đang tìm kiếm thông tin về 'square roots simplified calculator'.
Đơn Giản Hóa Căn Bậc Hai Bằng Máy Tính Đồ Thị