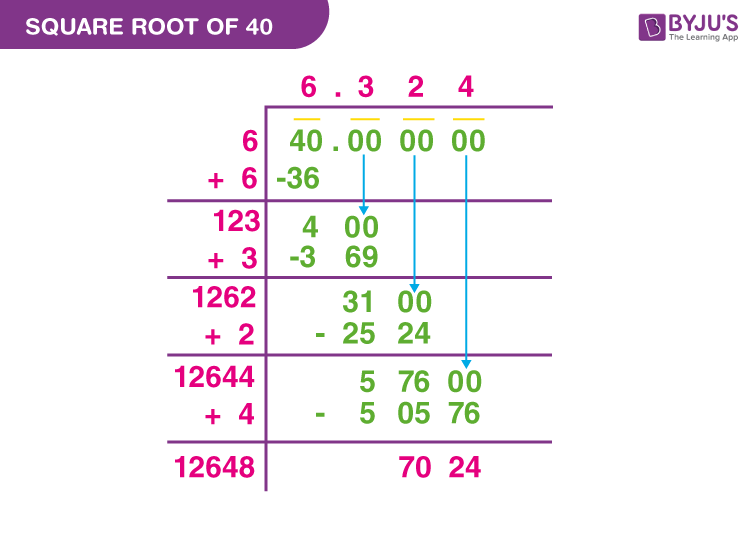
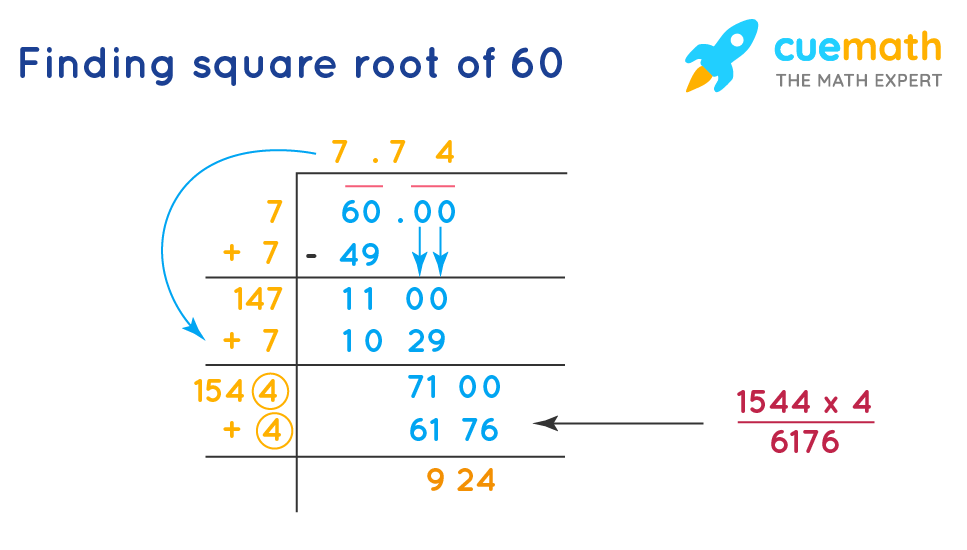
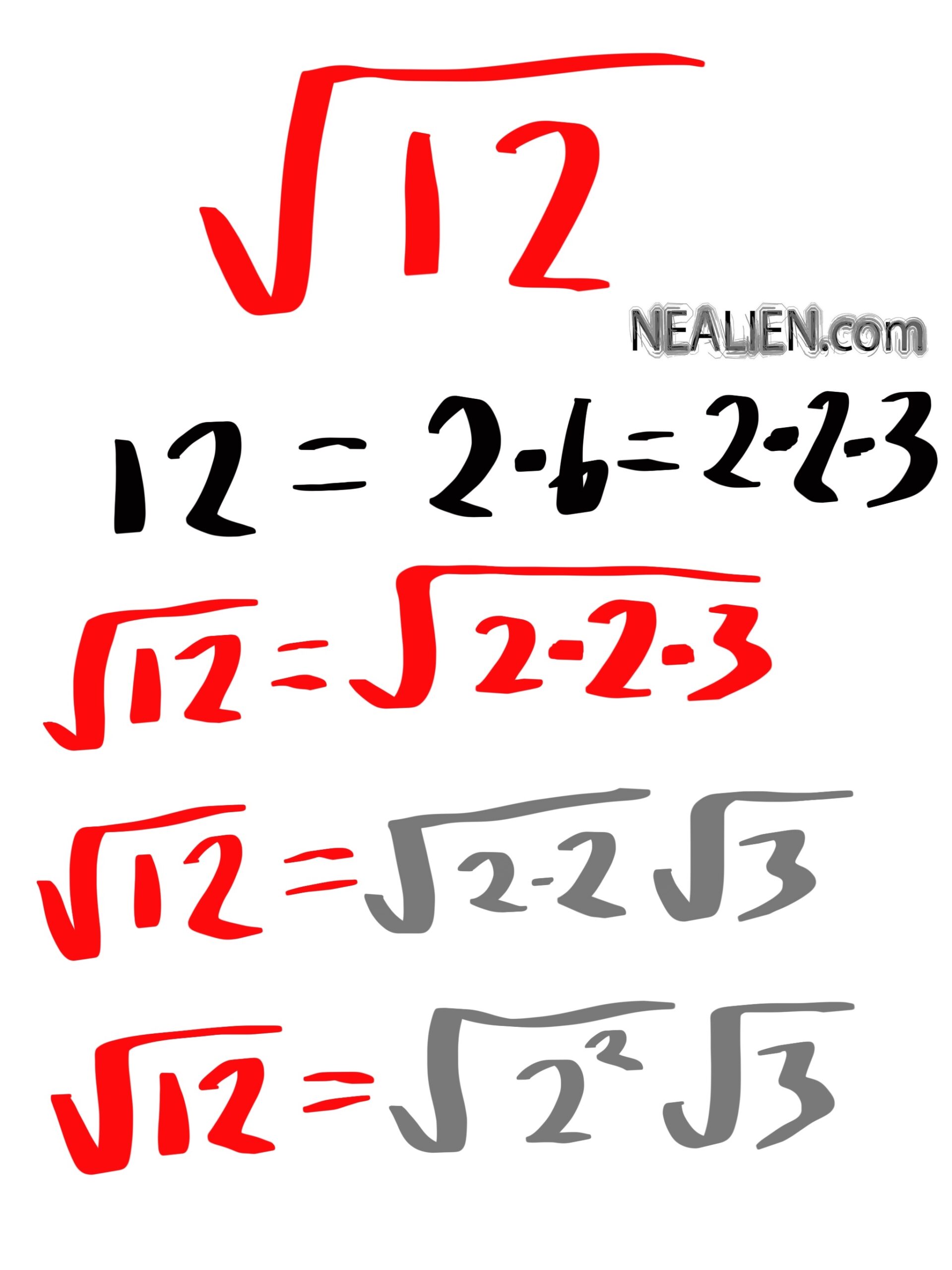Topic square root 60 simplified: Simplifying the square root of 60 can seem challenging, but with the right approach, it's straightforward. This article will guide you through easy steps to break down and simplify the square root of 60, making it understandable and manageable. Master this fundamental math skill and boost your confidence in solving similar problems!
Table of Content
- Simplifying the Square Root of 60
- Introduction to Square Roots
- Prime Factorization Method
- Steps to Simplify Square Root of 60
- Understanding Perfect Squares
- Separating Perfect Squares and Non-Perfect Squares
- Combining Simplified Parts
- Final Simplified Form of Square Root of 60
- Common Mistakes to Avoid
- Practical Applications of Simplified Square Roots
- Practice Problems and Solutions
- Frequently Asked Questions (FAQs)
- Conclusion
- YOUTUBE: Xem video để tìm hiểu cách đơn giản hóa căn bậc hai của 60 một cách dễ dàng và chính xác.
Simplifying the Square Root of 60
The process of simplifying the square root of a number involves finding the prime factors and simplifying the expression. Let's simplify the square root of 60 step by step.
Step-by-Step Simplification
- First, find the prime factorization of 60:
\[
60 = 2^2 \times 3 \times 5
\] - Next, apply the square root to the prime factors:
\[
\sqrt{60} = \sqrt{2^2 \times 3 \times 5}
\] - Simplify by separating the perfect square from the non-perfect squares:
\[
\sqrt{2^2 \times 3 \times 5} = \sqrt{2^2} \times \sqrt{3} \times \sqrt{5}
\] - Simplify the perfect square:
\[
\sqrt{2^2} = 2
\]
Final Simplified Form
Combining the simplified parts, we get:
\[
\sqrt{60} = 2 \sqrt{15}
\]
Thus, the square root of 60 simplified is \(2 \sqrt{15}\).

READ MORE:
Introduction to Square Roots
The concept of a square root is fundamental in mathematics and is essential for understanding more advanced math topics. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\).
Square roots are denoted by the radical symbol \(\sqrt{}\). For instance, the square root of 25 is written as \(\sqrt{25}\). Here are a few important points to consider:
- The square root of a perfect square is always an integer. For example, \(\sqrt{36} = 6\), since \(6 \times 6 = 36\).
- If the number is not a perfect square, its square root will be an irrational number. For example, \(\sqrt{2}\) is approximately 1.414 and cannot be expressed as a simple fraction.
- Square roots can be simplified by factoring the number into its prime factors and grouping the pairs of prime factors.
Understanding square roots is crucial for solving quadratic equations, working with exponents, and in various fields such as physics, engineering, and computer science.
Prime Factorization Method
Prime factorization is a method used to break down a composite number into its prime factors. This method is particularly useful for simplifying square roots. Here’s how you can use prime factorization to simplify the square root of 60.
- Find the prime factors of 60:
- Start by dividing 60 by the smallest prime number, which is 2: \(60 \div 2 = 30\).
- Continue factoring 30 by 2: \(30 \div 2 = 15\).
- Next, factor 15 by the next smallest prime number, which is 3: \(15 \div 3 = 5\).
- Finally, 5 is already a prime number.
So, the prime factorization of 60 is:
\[
60 = 2 \times 2 \times 3 \times 5 = 2^2 \times 3 \times 5
\] - Express the square root of 60 using its prime factors:
\[
\sqrt{60} = \sqrt{2^2 \times 3 \times 5}
\] - Simplify the square root by separating the perfect squares:
\[
\sqrt{2^2 \times 3 \times 5} = \sqrt{2^2} \times \sqrt{3} \times \sqrt{5}
\] - Calculate the square root of the perfect square:
\[
\sqrt{2^2} = 2
\] - Combine the simplified parts:
\[
\sqrt{60} = 2 \sqrt{15}
\]
Thus, using the prime factorization method, we have simplified the square root of 60 to \(2 \sqrt{15}\).
Steps to Simplify Square Root of 60
To simplify the square root of 60, we can use the prime factorization method. Here are the steps to simplify the square root of 60:
- Prime Factorization:
First, find the prime factorization of 60. Prime factors are the prime numbers that multiply together to give the original number.
60 can be factored into prime numbers as follows:
\(60 = 2 \times 2 \times 3 \times 5\)
- Group the Prime Factors:
Next, group the prime factors into pairs of the same number. Since we are finding the square root, we look for pairs of the same factor.
Here, we have a pair of 2s.
- Separate Perfect Squares and Non-Perfect Squares:
Rewrite the square root of 60 by separating the perfect square factors from the non-perfect square factors.
\(\sqrt{60} = \sqrt{2^2 \times 3 \times 5}\)
- Simplify the Square Root:
Take the square root of the perfect squares and simplify.
\(\sqrt{60} = \sqrt{2^2} \times \sqrt{3 \times 5}\)
\(\sqrt{60} = 2 \times \sqrt{15}\)
- Final Simplified Form:
The simplified form of the square root of 60 is:
\(\sqrt{60} = 2\sqrt{15}\)
Understanding Perfect Squares
Perfect squares are numbers that can be expressed as the product of an integer with itself. For example, \(1, 4, 9, 16,\) and \(25\) are perfect squares because:
- \(1 = 1 \times 1\)
- \(4 = 2 \times 2\)
- \(9 = 3 \times 3\)
- \(16 = 4 \times 4\)
- \(25 = 5 \times 5\)
In general, a number \(n\) is a perfect square if it can be written as \(n = k^2\) for some integer \(k\).
When simplifying square roots, identifying perfect squares within the radicand (the number inside the square root) can greatly simplify the process. For instance, to simplify \(\sqrt{60}\), we look for perfect squares that are factors of 60.
Steps to Identify Perfect Squares in a Number
- Factorize the number into its prime factors. For \(60\), the prime factorization is: \[ 60 = 2^2 \times 3 \times 5 \]
- Identify pairs of prime factors. Each pair represents a perfect square. In this case, \(2^2\) is a perfect square.
- Rewrite the number as the product of the identified perfect squares and the remaining factors: \[ 60 = 2^2 \times 15 \]
- Take the square root of each part separately: \[ \sqrt{60} = \sqrt{2^2 \times 15} = \sqrt{2^2} \times \sqrt{15} = 2 \sqrt{15} \]
This method allows us to simplify the square root of 60 to \(2\sqrt{15}\), demonstrating the importance of understanding perfect squares in simplifying square roots.
Separating Perfect Squares and Non-Perfect Squares
To simplify the square root of 60, we need to separate it into perfect square factors and non-perfect square factors. Here's how we do it:
-
Identify the prime factors of 60:
Prime factorization of 60 gives us: \(60 = 2^2 \times 3 \times 5\).
-
Separate the perfect squares:
From the prime factors, identify the perfect squares. In this case, \(2^2\) is a perfect square, while \(3\) and \(5\) are not.
Thus, we can write 60 as \(60 = 4 \times 15\) where 4 is a perfect square.
-
Rewrite the square root:
Express the square root of 60 using the perfect square and non-perfect square:
\(\sqrt{60} = \sqrt{4 \times 15} = \sqrt{4} \times \sqrt{15}\)
-
Simplify the square root:
Take the square root of the perfect square:
\(\sqrt{4} = 2\)
Therefore:
\(\sqrt{60} = 2 \times \sqrt{15} = 2\sqrt{15}\)
Thus, the simplified form of the square root of 60 is \(2\sqrt{15}\).
Combining Simplified Parts
To simplify the square root of 60, we need to break it down into its prime factors and identify the perfect squares. Here’s a step-by-step guide:
- First, find the prime factorization of 60:
- 60 = 2 × 30
- 30 = 2 × 15
- 15 = 3 × 5
So, the prime factorization of 60 is 2 × 2 × 3 × 5.
- Next, group the factors into pairs of perfect squares:
- 60 = (2 × 2) × (3 × 5)
Here, 2 × 2 is a perfect square.
- Take the square root of the perfect square and simplify:
- √60 = √(22 × 15)
- √60 = √(22) × √15
- √60 = 2 × √15
Therefore, the simplified form of the square root of 60 is:
This means that we have extracted the perfect square (which is 4 or 22) from under the radical sign, leaving the non-perfect square (15) still under the radical.
Final Simplified Form of Square Root of 60
To find the final simplified form of the square root of 60, we start by breaking it down into its prime factors. The number 60 can be factorized as:
60 = 2 × 2 × 3 × 5
Next, we group the factors into pairs of perfect squares:
\(\sqrt{60} = \sqrt{2^2 \times 15}\)
We can separate the square root of the product into the product of the square roots:
\(\sqrt{60} = \sqrt{2^2} \times \sqrt{15}\)
The square root of \(2^2\) is 2:
\(\sqrt{2^2} = 2\)
So, we have:
\(\sqrt{60} = 2 \times \sqrt{15}\)
Thus, the final simplified form of the square root of 60 is:
\(\boxed{2\sqrt{15}}\)
Common Mistakes to Avoid
Simplifying the square root of a number like 60 can sometimes lead to mistakes. Here are some common errors and how to avoid them:
- Incorrect Prime Factorization:
Ensure you correctly factorize 60 into its prime factors. The correct factorization is \(60 = 2^2 \times 3 \times 5\). Any mistake in this step will lead to an incorrect simplification.
- Missing Perfect Squares:
Don't forget to identify and separate perfect squares. For example, in \( \sqrt{60} \), recognize that \(4\) is a perfect square factor, so \( \sqrt{60} = \sqrt{4 \times 15} = 2\sqrt{15} \).
- Improper Handling of Radicals:
Ensure correct use of the product rule for radicals, which states \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). For \( \sqrt{60} \), apply this rule as \( \sqrt{4 \times 15} = \sqrt{4} \times \sqrt{15} = 2\sqrt{15} \).
- Errors in Multiplication:
When simplifying, double-check your multiplication. For instance, \( \sqrt{4} \times \sqrt{15} \) correctly simplifies to \( 2 \times \sqrt{15} \), not \( 2 \times 15 \).
- Misunderstanding Negative Signs:
Remember that the square root symbol represents the principal (non-negative) square root. Negative square roots are indicated separately, such as \( \sqrt{60} = \pm 2\sqrt{15} \).
- Overlooking Simplification Opportunities:
Always simplify as much as possible. For example, \( \sqrt{60} \) can be simplified to \( 2\sqrt{15} \), which is its simplest radical form.
By paying attention to these common mistakes and applying the correct steps, you can accurately simplify the square root of 60 and avoid errors.

Practical Applications of Simplified Square Roots
The concept of square roots, including simplified forms like , has many practical applications in various fields. Understanding these applications can help illustrate the importance and utility of square roots in real-world scenarios. Below are some detailed examples:
- Finance:
In finance, square roots are used to calculate stock market volatility, which is a measure of how much a stock’s price fluctuates over time. By taking the variance of stock returns and finding its square root, investors can assess the risk associated with a particular investment.
- Architecture:
Architects and engineers use square roots to determine the natural frequency of structures like buildings and bridges. This helps predict how these structures will respond to various loads, such as wind or traffic, ensuring their stability and safety.
- Science:
In scientific research, square roots are essential for various calculations. For instance, they are used to determine the speed of a moving object, the amount of radiation absorbed by materials, and the intensity of sound waves. These calculations are crucial for developing new technologies and understanding natural phenomena.
- Statistics:
Square roots are fundamental in statistics for calculating standard deviation, which is the square root of the variance. This measure indicates how spread out the data is from the mean, helping statisticians analyze data sets and make informed decisions based on their results.
- Geometry:
In geometry, square roots are used to compute the area and perimeter of shapes, solve problems involving right triangles, and apply the Pythagorean theorem. For example, calculating the length of a triangle’s side often involves finding the square root of the sum of the squares of the other two sides.
- Computer Science:
In computer programming, square roots are used in various applications such as encryption algorithms, image processing, and game physics. For example, encryption algorithms often use modular arithmetic and square roots to generate secure keys for data transmission.
- Navigation:
Square roots are used in navigation to calculate distances between points on a map or globe and estimate bearings or directions. Pilots, for instance, use square roots to determine the distance and direction between two points on a flight plan.
These examples illustrate how square roots are not just abstract mathematical concepts but practical tools used across different fields to solve real-world problems and improve various processes.
Practice Problems and Solutions
Here are some practice problems to help you understand the simplification of square roots, specifically the square root of 60. Follow the steps and check your answers with the provided solutions.
Problem 1: Simplify the square root of 75
- Find the prime factorization of 75: \(75 = 3 \times 5^2\)
- Separate the perfect squares and non-perfect squares: \(\sqrt{75} = \sqrt{3 \times 5^2} = \sqrt{3} \times \sqrt{5^2}\)
- Simplify the square root of the perfect square: \(\sqrt{5^2} = 5\)
- Combine the simplified parts: \(\sqrt{75} = 5\sqrt{3}\)
Answer: \(5\sqrt{3}\)
Problem 2: Simplify the square root of 45
- Find the prime factorization of 45: \(45 = 3^2 \times 5\)
- Separate the perfect squares and non-perfect squares: \(\sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}\)
- Simplify the square root of the perfect square: \(\sqrt{3^2} = 3\)
- Combine the simplified parts: \(\sqrt{45} = 3\sqrt{5}\)
Answer: \(3\sqrt{5}\)
Problem 3: Simplify the square root of 72
- Find the prime factorization of 72: \(72 = 2^3 \times 3^2\)
- Separate the perfect squares and non-perfect squares: \(\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^2 \times 2 \times 3^2} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2}\)
- Simplify the square roots of the perfect squares: \(\sqrt{2^2} = 2\) and \(\sqrt{3^2} = 3\)
- Combine the simplified parts: \(\sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Answer: \(6\sqrt{2}\)
Problem 4: Simplify the square root of 98
- Find the prime factorization of 98: \(98 = 2 \times 7^2\)
- Separate the perfect squares and non-perfect squares: \(\sqrt{98} = \sqrt{2 \times 7^2} = \sqrt{2} \times \sqrt{7^2}\)
- Simplify the square root of the perfect square: \(\sqrt{7^2} = 7\)
- Combine the simplified parts: \(\sqrt{98} = 7\sqrt{2}\)
Answer: \(7\sqrt{2}\)
Problem 5: Simplify the square root of 180
- Find the prime factorization of 180: \(180 = 2^2 \times 3^2 \times 5\)
- Separate the perfect squares and non-perfect squares: \(\sqrt{180} = \sqrt{2^2 \times 3^2 \times 5} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{5}\)
- Simplify the square roots of the perfect squares: \(\sqrt{2^2} = 2\) and \(\sqrt{3^2} = 3\)
- Combine the simplified parts: \(\sqrt{180} = 2 \times 3 \times \sqrt{5} = 6\sqrt{5}\)
Answer: \(6\sqrt{5}\)
Solutions
Make sure to check your answers:
- Problem 1: \(5\sqrt{3}\)
- Problem 2: \(3\sqrt{5}\)
- Problem 3: \(6\sqrt{2}\)
- Problem 4: \(7\sqrt{2}\)
- Problem 5: \(6\sqrt{5}\)
Frequently Asked Questions (FAQs)
Here are some common questions and answers related to the simplification of the square root of 60:
-
What is the square root of 60?
The square root of 60 is approximately 7.746. However, it can be simplified to \(2\sqrt{15}\).
-
How do you simplify the square root of 60?
To simplify the square root of 60, you factor it into prime factors:
\[
\sqrt{60} = \sqrt{2 \times 2 \times 3 \times 5} = 2\sqrt{15}.
\] -
Why is it important to simplify square roots?
Simplifying square roots makes them easier to work with in mathematical equations and helps in understanding the properties of numbers more clearly.
-
What are some common mistakes when simplifying square roots?
Common mistakes include not factoring completely, mispairing factors, and confusing multiplication and addition properties under the square root.
-
Can the square root of 60 be simplified further?
No, \(2\sqrt{15}\) is the simplest form of the square root of 60 since 15 has no perfect square factors other than 1.
Conclusion
Simplifying the square root of 60 involves breaking it down into its prime factors and separating the perfect squares from the non-perfect squares. Through the process of prime factorization, we express 60 as the product of 22, 3, and 5. This allows us to simplify the square root of 60 into its simplest radical form:
\[
\sqrt{60} = \sqrt{2^2 \times 15} = \sqrt{2^2} \times \sqrt{15} = 2\sqrt{15}
\]
The simplified form of the square root of 60 is \(2\sqrt{15}\). This method not only helps in simplifying square roots but also provides a clear understanding of the factors involved. By recognizing the importance of prime factorization and perfect squares, we can apply these principles to simplify other square roots effectively.
In conclusion, mastering the simplification of square roots, such as \(\sqrt{60}\), is essential for various mathematical applications, including solving equations and understanding geometric properties. Practicing these steps will enhance your mathematical skills and enable you to tackle more complex problems with confidence.
READ MORE:
Xem video để tìm hiểu cách đơn giản hóa căn bậc hai của 60 một cách dễ dàng và chính xác.
Đơn giản hóa căn bậc hai của 60: Sqrt(60)