Simplifying Square Roots Calculator: Your Ultimate Tool for Easy Calculations

Use this calculator to simplify square roots. Simplifying square roots involves expressing the square root in its simplest radical form. The calculator will help you break down the square root into its prime factors and simplify it.

How to Use the Simplifying Square Roots Calculator

1. Enter the number you want to simplify in the input box.
2. Click the "Simplify" button to see the simplified form of the square root.
3. The calculator will display the simplified radical form, as well as any possible integer results.

Examples of Simplifying Square Roots

• $$
  50 = 52
  

• $$
  72 = 62
  

• $$
  45 = 35
  

Benefits of Simplifying Square Roots

• Makes calculations easier and more manageable.
• Helps in understanding and solving algebraic expressions.
• Useful for simplifying the results in geometry and trigonometry.

Understanding Square Root Simplification

To simplify a square root, follow these steps:

1. Find the prime factors of the number inside the square root.
2. Group the prime factors into pairs.
3. Move one factor from each pair outside the square root.
4. Multiply the factors outside the square root.
5. If any prime factors are left inside, keep them under the square root symbol.

Practice Problems

Try simplifying these square roots on your own:

• $\sqrt{18}$
• $\sqrt{98}$
• $\sqrt{128}$

Frequently Asked Questions

Q: Why do we simplify square roots?

A: Simplifying square roots helps in making mathematical expressions simpler and easier to work with. It is especially useful in algebra, geometry, and higher-level math.

Q: Can all square roots be simplified?

A: Not all square roots can be simplified to an integer, but they can often be expressed in a simpler radical form.

Simplifying square roots involves breaking down a radical expression into its simplest form. This process helps in making calculations easier and is essential in various areas of mathematics, including algebra and geometry. Here's a detailed step-by-step guide on how to simplify square roots:

1. Identify the number under the square root.
2. Find the prime factors of this number.
3. Pair the prime factors in groups of two.
4. Move one factor from each pair outside the square root.
5. Multiply the factors outside the square root to get the simplified form.
6. If any factors are left inside, they remain under the square root symbol.

Let's consider an example to illustrate these steps:

• $$
  72 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 = 62
  

By following these steps, you can simplify any square root to its basic form. Using a simplifying square roots calculator can help automate this process, providing accurate and quick results.

A simplifying square roots calculator is an efficient tool for reducing square roots to their simplest form. Here’s a step-by-step guide on how to use it:

1. Enter the number you want to simplify into the calculator’s input box.
2. Click the "Simplify" button to initiate the calculation process.
3. The calculator will factorize the number under the square root into its prime factors.
4. It will then group the prime factors into pairs.
5. The calculator will move one factor from each pair outside the square root, leaving any unpaired factors under the radical.
6. Finally, the simplified form of the square root is displayed on the screen.

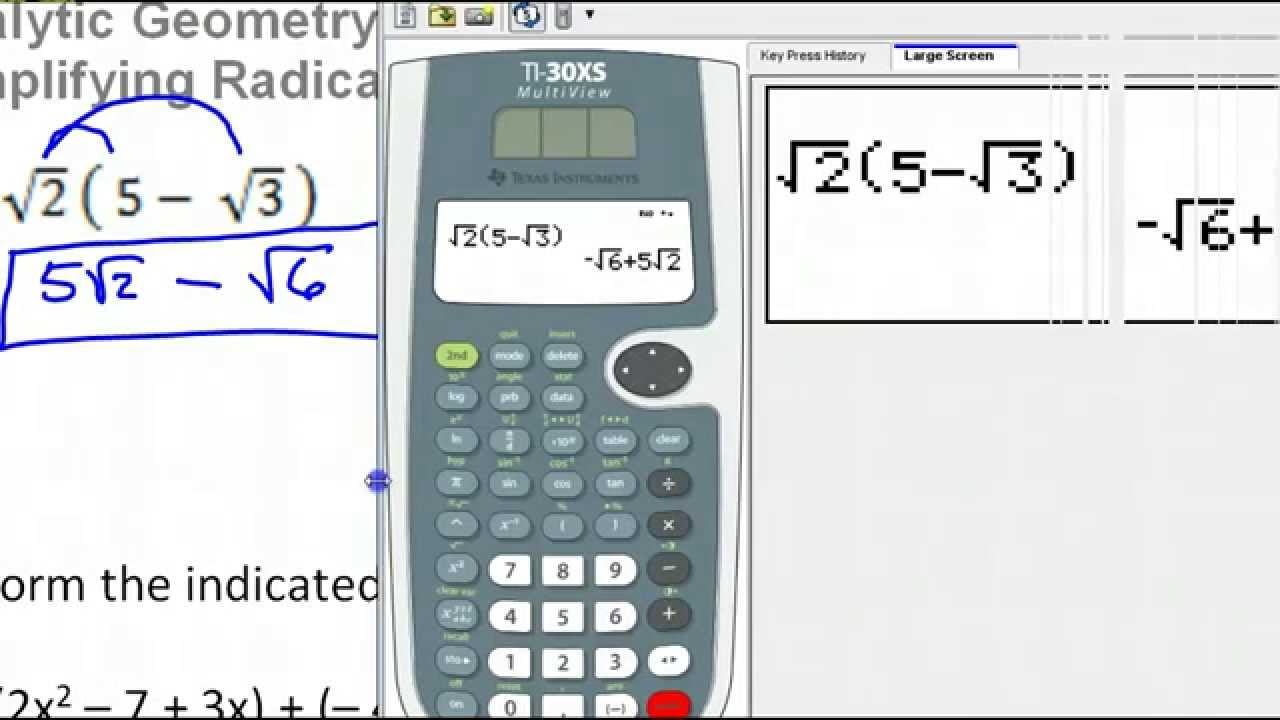
For example, to simplify \( \sqrt{50} \):

• Enter "50" into the calculator.
• Press "Simplify".
• The calculator will show: $\sqrt{50}=\sqrt{2\; \backslash cdot\; 5\; \backslash cdot\; 5}=\; 5\sqrt{2}$

This tool is invaluable for students and professionals who need quick and accurate simplifications of square roots. It saves time and ensures precision in mathematical computations.

Simplifying square roots involves reducing the expression to its simplest radical form. Follow these detailed steps to simplify square roots effectively:

1. Identify the number under the square root (radicand). For example, consider \( \sqrt{72} \).
2. Find the prime factors of the radicand. For 72, the prime factorization is \( 2 \times 2 \times 2 \times 3 \times 3 \).
3. Group the prime factors into pairs. In this case, \( (2 \times 2) \), \( (3 \times 3) \), and a single 2.
4. Move one factor from each pair outside the square root. Each pair of factors taken out of the radical becomes a single factor outside the radical.
5. Multiply the factors outside the square root. For our example:
   • \( (2 \times 3) = 6 \)
6. Any remaining unpaired factors stay inside the square root. Here, the remaining factor is 2.
7. Combine the results to get the simplified form:

   $$
   72 = 62
   

Let's look at another example to reinforce these steps:

• Consider \( \sqrt{50} \):
• Prime factorization of 50: \( 2 \times 5 \times 5 \)
• Group the factors: \( (5 \times 5) \) and a single 2.
• Move one 5 outside the square root:
• \( 5 \) remains inside the square root:

  $$
  50 = 52
  

By following this step-by-step process, you can simplify any square root expression to its simplest form.

Simplifying square roots can be easily understood through a few examples. Below are some detailed examples to illustrate the process step by step:

Example 1: Simplifying \( \sqrt{50} \)

1. Find the prime factors of 50: \( 50 = 2 \times 5 \times 5 \).
2. Group the factors into pairs: \( 2 \times (5 \times 5) \).
3. Move one factor from each pair outside the square root: \( 5 \) comes out of the square root.
4. Combine the results:

   $$
   50 = 52
   

Example 2: Simplifying \( \sqrt{72} \)

1. Find the prime factors of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
2. Group the factors into pairs: \( (2 \times 2) \times 2 \times (3 \times 3) \).
3. Move one factor from each pair outside the square root: \( 2 \) and \( 3 \) come out of the square root.
4. Combine the results:

   $$
   72 = 62
   

Example 3: Simplifying \( \sqrt{98} \)

1. Find the prime factors of 98: \( 98 = 2 \times 7 \times 7 \).
2. Group the factors into pairs: \( 2 \times (7 \times 7) \).
3. Move one factor from each pair outside the square root: \( 7 \) comes out of the square root.
4. Combine the results:

   $$
   98 = 72
   

Example 4: Simplifying \( \sqrt{128} \)

1. Find the prime factors of 128: \( 128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \).
2. Group the factors into pairs: \( (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2 \).
3. Move one factor from each pair outside the square root: \( 2 \times 2 \times 2 \) come out of the square root.
4. Combine the results:

   $$
   128 = 82
   

These examples demonstrate the systematic process of simplifying square roots by factoring, pairing, and reducing the radicand to its simplest form.

A square root simplification calculator is a powerful tool that offers several advantages for students, educators, and professionals. Here are the key benefits of using this calculator:

• Accuracy: The calculator ensures precise results, reducing the risk of human error in manual calculations. This accuracy is crucial for complex mathematical problems.
• Efficiency: It saves time by quickly simplifying square roots, which is especially beneficial when dealing with large numbers or multiple calculations.
• Convenience: The calculator is user-friendly and can be accessed online, making it easy to use from any device without the need for additional tools or software.
• Learning Aid: For students, it serves as an excellent learning tool. By showing step-by-step solutions, it helps students understand the process of simplifying square roots, enhancing their math skills.
• Consistency: The calculator provides consistent results, which is essential for verifying homework, assignments, or any mathematical work requiring simplification of square roots.
• Application in Various Fields: Simplified square roots are used in numerous fields, including physics, engineering, and computer science. The calculator assists professionals in these areas by providing quick and accurate simplifications.
• Supports Advanced Calculations: For higher-level mathematics, where square roots are part of more complex expressions, the calculator helps in breaking down and simplifying these expressions efficiently.

In summary, a square root simplification calculator is an indispensable tool that enhances accuracy, efficiency, and understanding in mathematical computations. Whether for educational purposes or professional applications, it streamlines the process of simplifying square roots, making it an invaluable resource.

Prime factorization is a crucial step in simplifying square roots. It involves breaking down a number into its prime factors, which are the building blocks of the number. Here’s a detailed guide on how prime factorization is used in square root simplification:

1. Identify the number under the square root (radicand). For example, consider \( \sqrt{72} \).
2. Find the prime factors of the radicand. This is done by dividing the number by the smallest prime number (starting with 2) and continuing the process with the quotient until all factors are prime.
   • 72 ÷ 2 = 36
   • 36 ÷ 2 = 18
   • 18 ÷ 2 = 9
   • 9 ÷ 3 = 3
   • 3 ÷ 3 = 1
   So, the prime factors of 72 are \( 2 \times 2 \times 2 \times 3 \times 3 \).
3. Group the prime factors into pairs:
   • \((2 \times 2)\)
   • \((3 \times 3)\)
   • and a single 2 remaining.
4. Move one factor from each pair outside the square root:

   $$
   

5. The simplified form of \( \sqrt{72} \) is \( 6\sqrt{2} \).

Let’s look at another example to reinforce the concept:

Example: Simplifying \( \sqrt{200} \)

1. Prime factorization of 200:
   • 200 ÷ 2 = 100
   • 100 ÷ 2 = 50
   • 50 ÷ 2 = 25
   • 25 ÷ 5 = 5
   • 5 ÷ 5 = 1
   So, the prime factors of 200 are \( 2 \times 2 \times 2 \times 5 \times 5 \).
2. Group the factors into pairs:
   • \((2 \times 2)\)
   • \((5 \times 5)\)
   • and a single 2 remaining.
3. Move one factor from each pair outside the square root:

   $$
   

4. The simplified form of \( \sqrt{200} \) is \( 10\sqrt{2} \).

Prime factorization is fundamental in simplifying square roots, making it easier to manage and solve mathematical problems involving radicals.

Simplifying square roots that contain variables involves similar steps as simplifying numerical square roots. The goal is to factor the expression under the square root into a product of squares, allowing you to simplify it further. Here’s a step-by-step guide:

1. Identify Perfect Squares:

   Look for perfect square factors within the numerical part and the variable part of the radicand (the expression under the square root).

2. Separate the Expression:

   Rewrite the radicand as a product of its factors, separating the perfect squares from the non-perfect squares.

3. Simplify the Perfect Squares:

   Take the square root of the perfect square factors. For variables, use the property \( \sqrt{x^2} = x \).

4. Combine the Results:

   Multiply the simplified parts together to get the final simplified form.

Here are some examples to illustrate the process:

Example 1

Simplify \( \sqrt{50x^2} \)

1. Identify perfect squares in \( 50x^2 \):
   • 50 = 25 × 2
   • \( x^2 \) is a perfect square
2. Rewrite as:

   \( \sqrt{25 \cdot 2 \cdot x^2} \)

3. Simplify:

   \( \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^2} = 5 \cdot \sqrt{2} \cdot x \)

4. Final answer:

   \( 5x\sqrt{2} \)

Example 2

Simplify \( \sqrt{72x^3y^2} \)

1. Identify perfect squares in \( 72x^3y^2 \):
   • 72 = 36 × 2
   • \( x^3 = x^2 \cdot x \)
   • \( y^2 \) is a perfect square
2. Rewrite as:

   \( \sqrt{36 \cdot 2 \cdot x^2 \cdot x \cdot y^2} \)

3. Simplify:

   \( \sqrt{36} \cdot \sqrt{2} \cdot \sqrt{x^2} \cdot \sqrt{x} \cdot \sqrt{y^2} = 6 \cdot \sqrt{2} \cdot x \cdot \sqrt{x} \cdot y \)

4. Combine like terms:

   \( 6xy\sqrt{2x} \)

5. Final answer:

   \( 6xy\sqrt{2x} \)

By following these steps, you can simplify square roots with variables efficiently. Practicing these methods will help you become more comfortable with handling more complex expressions.

Simplifying square roots can be tricky, and there are several common mistakes that students often make. Understanding these pitfalls and how to avoid them will help you simplify square roots correctly and efficiently.

• Ignoring the Properties of Square Roots:

  One common mistake is overlooking the fundamental properties of square roots, such as \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \). Always apply these properties correctly to simplify expressions.

• Incorrect Prime Factorization:

  Failing to correctly factor a number into its prime factors can lead to incorrect simplifications. Double-check your factorization using a factor tree or other methods to ensure accuracy.

• Overlooking Perfect Squares:

  Not recognizing perfect squares within a radical can make the simplification process harder. Familiarize yourself with common perfect squares (e.g., \(4, 9, 16, 25, \ldots\)) to quickly identify and extract them from under the radical.

• Misapplying Negative Signs:

  Misunderstanding how to handle negative signs with square roots, especially when dealing with imaginary numbers, is a frequent error. Remember that \( \sqrt{-a} \) is not the same as \( -\sqrt{a} \); the former involves an imaginary unit \( i \), where \( \sqrt{-a} = \sqrt{a} \cdot i \).

• Confusing Addition and Multiplication Rules:

  A common error is confusing the rules for adding and multiplying square roots. Remember that \( \sqrt{a} + \sqrt{b} \neq \sqrt{a + b} \), while \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \). Applying these rules correctly is crucial for accurate simplification.

To avoid these common mistakes, follow these tips:

• Practice Regularly:

  Regular practice with a variety of problems helps reinforce the correct methods and principles.

• Use Checkpoints:

  After each simplification step, verify the results against known principles or use a calculator to check your work.

• Seek Clarification:

  If you’re unsure about a concept or a step in the simplification process, don’t hesitate to seek help from teachers, tutors, or online resources.

• Learn from Mistakes:

  Reviewing mistakes and understanding where you went wrong is a powerful learning tool. This approach helps you avoid similar errors in the future.

By being aware of these common mistakes and adopting strategies to avoid them, you can enhance your skills in simplifying square roots and improve your overall mathematical proficiency.

In this section, we will explore advanced techniques for simplifying square roots, focusing on the product and quotient rules, as well as rationalizing denominators and handling expressions with variables.

1. Using the Product Rule

The product rule states that the square root of a product is the product of the square roots. Mathematically, this can be written as:

\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]

Here are the steps to simplify using the product rule:

1. Factor any perfect squares from the radicand.
2. Write the radical expression as a product of radical expressions.
3. Simplify the expression.

For example:

\[\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\]

2. Using the Quotient Rule

The quotient rule states that the square root of a quotient is the quotient of the square roots:

\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]

Here are the steps to simplify using the quotient rule:

1. Write the radical expression as the quotient of two radical expressions.
2. Simplify the numerator and the denominator separately.

For example:

\[\sqrt{\frac{50}{2}} = \frac{\sqrt{50}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{2}} = 5\]

3. Rationalizing the Denominator

Rationalizing the denominator involves eliminating radicals from the denominator of a fraction. This can be achieved by multiplying the numerator and the denominator by a suitable radical that will make the denominator a perfect square:

1. Identify the radical in the denominator.
2. Multiply the numerator and the denominator by this radical.
3. Simplify the resulting expression.

For example:

\[\frac{3}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}\]

4. Simplifying Square Roots with Variables

When dealing with square roots that include variables, we apply the same principles as with numerical radicands but include variable properties:

1. Factor any perfect squares from the numerical and variable parts of the radicand.
2. Express the radicand as a product of perfect squares and other factors.
3. Simplify each part separately.

For example:

\[\sqrt{18x^4y^3} = \sqrt{9 \cdot 2 \cdot x^4 \cdot y^2 \cdot y} = 3x^2y\sqrt{2y}\]

5. Handling Higher Index Roots

Sometimes we encounter roots higher than the square root, such as cube roots. The general rule for any root can be stated as:

\[\sqrt[n]{a^m} = a^{\frac{m}{n}}\]

For example, simplifying a cube root:

\[\sqrt[3]{64x^9} = (64x^9)^{\frac{1}{3}} = 4x^3\]

These techniques can greatly simplify complex radical expressions, making them more manageable for further mathematical operations.

Here are some practice problems to help you master the art of simplifying square roots. Try to solve each problem step-by-step, and then check your solutions below.

Problem 1: Simplify \( \sqrt{50} \)

Solution:

1. Factor the radicand into prime factors: \( 50 = 2 \times 5^2 \)
2. Apply the square root to each factor: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
3. Separate the square root of the perfect square: \( \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2} \)
4. Simplify: \( \sqrt{2} \times 5 = 5\sqrt{2} \)

Problem 2: Simplify \( \sqrt{72} \)

Solution:

1. Factor the radicand into prime factors: \( 72 = 2^3 \times 3^2 \)
2. Apply the square root to each factor: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
3. Separate the square root of the perfect square: \( \sqrt{2^3 \times 3^2} = \sqrt{2^3} \times \sqrt{3^2} \)
4. Simplify: \( \sqrt{2^3} \times 3 = \sqrt{8} \times 3 = 2\sqrt{2} \times 3 = 6\sqrt{2} \)

Problem 3: Simplify \( 3\sqrt{18} + 2\sqrt{50} \)

Solution:

1. Simplify each square root separately:
• \( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \)
• \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \)
2. Substitute the simplified forms back into the expression:
• \( 3\sqrt{18} = 3 \times 3\sqrt{2} = 9\sqrt{2} \)
• \( 2\sqrt{50} = 2 \times 5\sqrt{2} = 10\sqrt{2} \)
3. Combine the terms: \( 9\sqrt{2} + 10\sqrt{2} = 19\sqrt{2} \)

Problem 4: Simplify \( \sqrt{48} \)

Solution:

1. Factor the radicand into prime factors: \( 48 = 2^4 \times 3 \)
2. Apply the square root to each factor: \( \sqrt{48} = \sqrt{2^4 \times 3} \)
3. Separate the square root of the perfect square: \( \sqrt{2^4 \times 3} = \sqrt{2^4} \times \sqrt{3} \)
4. Simplify: \( 2^2 \sqrt{3} = 4\sqrt{3} \)

Problem 5: Simplify \( \sqrt{75} - \sqrt{27} \)

Solution:

1. Simplify each square root separately:
• \( \sqrt{75} = \sqrt{3 \times 5^2} = 5\sqrt{3} \)
• \( \sqrt{27} = \sqrt{3^3} = 3\sqrt{3} \)
2. Subtract the terms: \( 5\sqrt{3} - 3\sqrt{3} = (5 - 3)\sqrt{3} = 2\sqrt{3} \)

Simplifying square roots is a fundamental skill in mathematics, providing a basis for more advanced topics in algebra, geometry, and beyond. By understanding the methods and techniques involved, such as prime factorization, using the product and quotient rules, and handling variables, you can solve a wide range of problems more efficiently.

Here are some key takeaways to remember:

• Prime factorization is essential for breaking down the radicand into simpler components.
• The product rule helps in combining or separating square roots effectively.
• The quotient rule is useful for simplifying fractions under a square root.
• Practicing with variables prepares you for more complex algebraic expressions.

For those looking to deepen their understanding or seeking additional practice, consider the following resources:

• - An interactive tool for solving square root problems step-by-step.
• - A comprehensive guide with detailed examples and practice problems.
• - A versatile tool for simplifying square roots, including complex numbers.

By utilizing these resources and continuing to practice, you can master the skill of simplifying square roots, enhancing your mathematical proficiency and confidence.