Topic calculator for simplifying radical expressions: Discover how to effectively use a calculator for simplifying radical expressions with our comprehensive guide. Learn step-by-step methods and useful tips to simplify radicals effortlessly, ensuring accuracy and efficiency in your mathematical calculations.
Table of Content
- Calculator for Simplifying Radical Expressions
- Introduction to Simplifying Radical Expressions
- Understanding Radical Expressions
- Basic Rules for Simplifying Radicals
- Methods for Simplifying Radicals
- Using a Calculator for Simplifying Radicals
- Step-by-Step Guide to Simplifying Radicals
- Examples of Simplifying Radicals
- Common Mistakes to Avoid
- Practice Problems for Simplifying Radicals
- Benefits of Simplifying Radical Expressions
- Conclusion and Recap
- YOUTUBE: Hướng dẫn sử dụng máy tính ClassWiz để đơn giản hóa biểu thức căn. Video này sẽ giúp bạn làm quen với các chức năng của máy tính ClassWiz trong việc giải các bài toán liên quan đến biểu thức căn.
Calculator for Simplifying Radical Expressions
This online calculator is designed to simplify radical expressions, making it easy to work with square roots, cube roots, and higher-order roots. Use this tool to streamline your math problems and achieve accurate results quickly.
Features
- Simplifies square roots, cube roots, and higher-order roots
- Handles both numerical and algebraic expressions
- Provides step-by-step solutions
- User-friendly interface
How to Use the Calculator
- Enter the radical expression you want to simplify in the input box.
- Click the "Simplify" button to process the expression.
- View the simplified expression and the steps taken to reach the solution.
Examples
| Expression | Simplified Form | Steps |
| \(\sqrt{50}\) | \(5\sqrt{2}\) | \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\) |
| \(\sqrt[3]{54}\) | \(3\sqrt[3]{2}\) | \(\sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \cdot \sqrt[3]{2} = 3\sqrt[3]{2}\) |
| \(\sqrt{75x^2}\) | \(5x\sqrt{3}\) | \(\sqrt{75x^2} = \sqrt{25 \times 3 \times x^2} = 5x\sqrt{3}\) |
Try the calculator now and simplify your radical expressions with ease!
READ MORE:
Introduction to Simplifying Radical Expressions
Simplifying radical expressions involves manipulating square roots to their simplest form, often using mathematical operations and rules specific to radicals. Here’s a detailed approach to understanding and mastering this process:
- Radical Basics: Begin with understanding what radicals are and how they relate to square roots.
- Radical Simplification Rules: Learn the fundamental rules for simplifying radicals, including how to handle different indexes and radicands.
- Step-by-Step Methods: Explore systematic methods for simplifying radicals, from basic examples to complex expressions.
- Common Techniques: Discover common techniques such as factoring, reducing, and using conjugates to simplify radicals efficiently.
- Calculator Usage: Understand when and how to use calculators effectively for simplifying radical expressions, ensuring accuracy and speed.
Mastering radical simplification enhances your ability to handle mathematical problems involving square roots and prepares you for more advanced mathematical concepts.
Understanding Radical Expressions
Radical expressions are mathematical expressions that include a root symbol, such as a square root or cube root. Simplifying these expressions can often make them easier to work with in equations and other calculations. To gain a better understanding of radical expressions, let's explore their components, basic rules, and examples of how to simplify them.
Components of Radical Expressions
A radical expression consists of three main parts:
- Radicand: The number or expression inside the root symbol.
- Index: The small number outside and to the left of the root symbol that indicates the degree of the root. If the index is not specified, it is assumed to be 2 (square root).
- Radical symbol: The root symbol (√) itself.
Basic Rules for Simplifying Radicals
When simplifying radicals, certain rules must be followed to ensure the expression is in its simplest form:
- Factor the radicand into its prime factors.
- Apply the rule that \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
- Identify and separate perfect squares (or cubes, etc.) from the radicand.
- Simplify the radical by taking the square root (or cube root, etc.) of the perfect squares.
Examples of Simplifying Radical Expressions
Let's go through some examples to illustrate these steps:
Example 1: Simplify \(\sqrt{75}\)
First, factor 75 into its prime factors: \(75 = 3 \cdot 5^2\).
Next, apply the square root to each factor: \(\sqrt{75} = \sqrt{3 \cdot 5^2} = 5\sqrt{3}\).
Example 2: Simplify \(\sqrt[3]{54}\)
First, factor 54 into its prime factors: \(54 = 2 \cdot 3^3\).
Next, apply the cube root to each factor: \(\sqrt[3]{54} = \sqrt[3]{2 \cdot 3^3} = 3\sqrt[3]{2}\).
Example 3: Simplify \(\sqrt{12} + \sqrt{75}\)
First, simplify each radical individually:
\(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\)
\(\sqrt{75} = \sqrt{25 \cdot 3} = 5\sqrt{3}\)
Next, combine the simplified radicals: \(2\sqrt{3} + 5\sqrt{3} = 7\sqrt{3}\).
Using Calculators for Simplifying Radicals
Several online calculators can help simplify radical expressions quickly and accurately. These tools follow the same rules and steps we discussed, ensuring that your results are correct and in the simplest form possible. Some popular options include:
Basic Rules for Simplifying Radicals
Simplifying radical expressions involves applying a set of fundamental rules to reduce them to their simplest form. Here are the basic rules:
- The Product Rule for Radicals: If you have two radicals multiplied together, you can combine them under a single radical. For example:
\(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
- The Quotient Rule for Radicals: If you have a radical divided by another radical, you can combine them under a single radical. For example:
\(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)
- Simplifying Radicals with perfect squares: To simplify a radical, factor the number inside the radical to find perfect squares. For example:
\(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\)
- Combining Like Radicals: You can combine radicals that have the same index and radicand. For example:
\(3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2}\)
- Rationalizing the Denominator: To remove a radical from the denominator, multiply the numerator and the denominator by the radical in the denominator. For example:
\(\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
Examples:
- Example 1: Simplify \(\sqrt{72}\)
- Step 1: Factor 72 into its prime factors: \(72 = 36 \cdot 2 = 6^2 \cdot 2\)
- Step 2: Apply the product rule: \(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2}\)
- Step 3: Simplify the perfect square: \(\sqrt{36} = 6\)
- Result: \(\sqrt{72} = 6\sqrt{2}\)
- Example 2: Simplify \(\frac{\sqrt{18}}{\sqrt{2}}\)
- Step 1: Apply the quotient rule: \(\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}}\)
- Step 2: Simplify inside the radical: \(\sqrt{9} = 3\)
- Result: \(\frac{\sqrt{18}}{\sqrt{2}} = 3\)
- Example 3: Simplify \(3\sqrt{8} + 2\sqrt{8}\)
- Step 1: Combine like radicals: \(3\sqrt{8} + 2\sqrt{8} = (3 + 2)\sqrt{8}\)
- Step 2: Simplify: \(5\sqrt{8}\)
- Step 3: Factor 8: \(8 = 4 \cdot 2\)
- Step 4: Simplify the perfect square: \(\sqrt{4} = 2\)
- Result: \(5\sqrt{8} = 5 \cdot 2\sqrt{2} = 10\sqrt{2}\)
Methods for Simplifying Radicals
Simplifying radicals involves various methods that help break down and reduce radical expressions to their simplest form. Here are some common methods:
Prime Factorization Method
Prime factorization involves breaking down the number inside the radical (the radicand) into its prime factors and then simplifying.
- Find the prime factors of the radicand.
- Group the prime factors in pairs (for square roots).
- Move each pair of prime factors outside the radical.
Example: Simplify \( \sqrt{72} \)
- Prime factorization of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group the pairs: \( 72 = (2 \times 2) \times (3 \times 3) \times 2 \)
- Simplify: \( \sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
Division Method
This method involves dividing the radicand by the highest perfect square factor.
- Identify the largest perfect square factor of the radicand.
- Rewrite the radicand as a product of this factor and another number.
- Simplify the expression by taking the square root of the perfect square factor.
Example: Simplify \( \sqrt{50} \)
- Largest perfect square factor of 50: \( 25 \)
- Rewrite: \( 50 = 25 \times 2 \)
- Simplify: \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \)
Rationalizing the Denominator
This method is used when a radical appears in the denominator of a fraction. Multiply the numerator and the denominator by a suitable radical to eliminate the radical from the denominator.
- Identify the radical in the denominator.
- Multiply the numerator and the denominator by a radical that will give a perfect square in the denominator.
- Simplify the resulting expression.
Example: Simplify \( \frac{5}{\sqrt{3}} \)
- Multiply by \( \frac{\sqrt{3}}{\sqrt{3}} \): \( \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \)
- Simplify: \( \frac{5\sqrt{3}}{3} \)
Using Calculators
Several online calculators can simplify radical expressions quickly and accurately. These calculators can handle various operations, including addition, subtraction, multiplication, division, and rationalizing denominators.
For instance, you can enter an expression like \( \sqrt{72} \) or \( \frac{5}{\sqrt{3}} \) into the calculator, and it will provide the simplified form instantly.
Example of using a calculator: Simplify \( \sqrt{45} \)
- Enter \( \sqrt{45} \) into the calculator.
- The calculator simplifies it to \( 3\sqrt{5} \).
Combining Like Radicals
When adding or subtracting radicals, ensure the radicals have the same radicand and root. Combine the coefficients of the like radicals.
- Ensure the radicands and roots are identical.
- Add or subtract the coefficients of the like radicals.
Example: Simplify \( 3\sqrt{2} + 5\sqrt{2} \)
- Combine like terms: \( 3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2} \)
Handling Higher-Order Roots
For radicals involving cube roots or higher-order roots, use similar methods but group factors accordingly.
- Identify the prime factors of the radicand.
- Group the factors in sets corresponding to the root's order.
- Move each complete set outside the radical.
Example: Simplify \( \sqrt[3]{54} \)
- Prime factorization of 54: \( 54 = 2 \times 3 \times 3 \times 3 \)
- Group the factors for cube root: \( 54 = (3 \times 3 \times 3) \times 2 \)
- Simplify: \( \sqrt[3]{54} = 3\sqrt[3]{2} \)
Practice Problems
Try simplifying the following radicals using the methods described above:
- Simplify \( \sqrt{98} \)
- Simplify \( \frac{7}{\sqrt{5}} \)
- Simplify \( \sqrt[3]{16} \)
Use these methods and practice problems to master simplifying radicals!

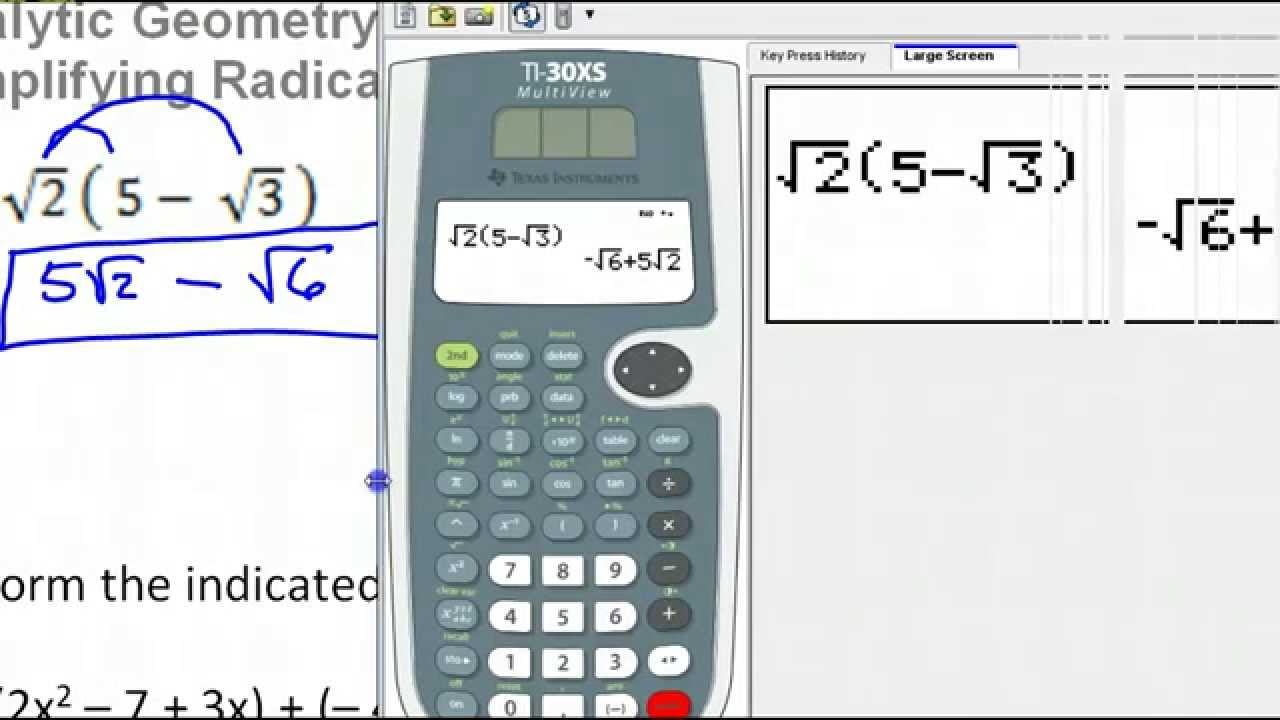
Using a Calculator for Simplifying Radicals
Simplifying radical expressions can be made much easier with the use of online calculators. These tools not only provide the simplified form but also show the steps involved, helping you understand the process. Here is a detailed guide on how to use such calculators effectively:
-
Select the Operation:
Choose the type of operation you want to perform. Most calculators offer options such as simplifying, adding, subtracting, multiplying, and dividing radicals. For instance, if you want to simplify a radical expression, select the 'simplify' option.
-
Input the Radical Expression:
Enter the radical expression into the calculator. This typically involves typing in the coefficients, the radicand (the number under the radical), and the index (if it is not a square root). For example, to simplify \( \sqrt{50} \), you would enter 50 as the radicand.
-
Execute the Calculation:
Click the calculate button to process the entered expression. The calculator will break down the expression into its prime factors and simplify it by extracting the largest perfect square factor. For example, \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \).
-
View Step-by-Step Solution:
Most calculators provide a step-by-step explanation of the simplification process. This helps in understanding how the solution was derived and can be a valuable learning tool.
Here is an example of using a calculator to simplify a radical expression:
| Expression | Input | Steps | Result |
| \( \sqrt{75} + \sqrt{12} \) | 75, 12 |
|
\( 7\sqrt{3} \) |
Using these calculators saves time and ensures accuracy, making them an invaluable tool for students and professionals alike.
Step-by-Step Guide to Simplifying Radicals
In this section, we will go through a detailed, step-by-step process for simplifying radical expressions.
-
Identify the Radicand:
First, determine the number or expression under the radical sign. For example, in \(\sqrt{50}\), the radicand is 50.
-
Find the Prime Factors:
Break down the radicand into its prime factors. For 50, the prime factors are \(2 \times 5^2\).
-
Separate Perfect Squares:
Identify and separate the perfect squares from the prime factors. In this case, \(50 = 2 \times 25 = 2 \times 5^2\).
-
Simplify the Radical:
Take the square root of the perfect squares and move them outside the radical. Here, \(\sqrt{50} = \sqrt{2 \times 25} = 5\sqrt{2}\).
-
Combine Like Terms (if applicable):
If you have multiple radicals, combine the like terms. For example, \(3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}\).
-
Final Answer:
The simplified form of the original radical expression is your final answer. In this example, \(\sqrt{50} = 5\sqrt{2}\).
Let's look at a more complex example:
Example: Simplify \(\sqrt{72}\).
-
Identify the Radicand: 72
-
Find the Prime Factors: \(72 = 2^3 \times 3^2\)
-
Separate Perfect Squares: \(72 = 2^2 \times 2 \times 3^2\)
-
Simplify the Radical: \(\sqrt{72} = \sqrt{2^2 \times 2 \times 3^2} = 2 \times 3 \sqrt{2} = 6\sqrt{2}\)
Using this step-by-step method, you can simplify any radical expression. For more complex expressions or to verify your work, using a calculator for simplifying radicals can be very helpful.
Examples of Simplifying Radicals
Here are several examples demonstrating how to simplify radical expressions step-by-step:
Example 1: Simplify \(\sqrt{75}\)
- First, factor the radicand (the number under the square root): \[ \sqrt{75} = \sqrt{25 \cdot 3} \]
- Next, take the square root of any perfect square factors: \[ \sqrt{25 \cdot 3} = \sqrt{25} \cdot \sqrt{3} = 5\sqrt{3} \]
- The simplified form is: \[ 5\sqrt{3} \]
Example 2: Simplify \(\sqrt{12}\)
- Factor the radicand: \[ \sqrt{12} = \sqrt{4 \cdot 3} \]
- Take the square root of the perfect square factor: \[ \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3} \]
- The simplified form is: \[ 2\sqrt{3} \]
Example 3: Add \(\sqrt{75} + \sqrt{12}\)
- First, simplify each radical expression: \[ \sqrt{75} = 5\sqrt{3} \] \[ \sqrt{12} = 2\sqrt{3} \]
- Combine like terms (terms with the same radicand): \[ 5\sqrt{3} + 2\sqrt{3} = (5 + 2)\sqrt{3} = 7\sqrt{3} \]
Example 4: Multiply \(\sqrt{18} \times \sqrt{14}\)
- Use the property of radicals: \[ \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \]
- Multiply the radicands: \[ \sqrt{18} \times \sqrt{14} = \sqrt{18 \times 14} \]
- Simplify inside the radical: \[ \sqrt{252} = \sqrt{36 \cdot 7} = 6\sqrt{7} \]
- The simplified form is: \[ 6\sqrt{7} \]
Example 5: Simplify \(\sqrt[3]{54}\)
- Factor the radicand into prime factors: \[ 54 = 2 \times 3^3 \]
- Apply the cube root: \[ \sqrt[3]{54} = \sqrt[3]{2 \times 3^3} = \sqrt[3]{2} \times \sqrt[3]{3^3} = \sqrt[3]{2} \times 3 \]
- The simplified form is: \[ 3\sqrt[3]{2} \]
Using these examples, you can practice simplifying radicals and better understand the process.
Common Mistakes to Avoid
Simplifying radicals can be tricky, and there are common mistakes students often make. Here are some key pitfalls to avoid:
- Incorrect Factorization: Ensure you correctly identify the prime factors of the radicand. For example, \(\sqrt{50}\) should be factored as \( \sqrt{25 \times 2} \), which simplifies to \( 5\sqrt{2} \), not \( \sqrt{5 \times 10} \).
- Combining Non-Like Radicals: Only like radicals (same radicand and index) can be combined. For instance, \(\sqrt{3} + \sqrt{12}\) cannot be directly combined because the radicands are different. Simplify \(\sqrt{12}\) first: \(\sqrt{4 \times 3} = 2\sqrt{3}\), then \(\sqrt{3} + 2\sqrt{3} = 3\sqrt{3}\).
- Forgetting to Simplify Completely: Always check if the radical can be simplified further. For example, \(\sqrt{18}\) simplifies to \(3\sqrt{2}\), but stopping at \(\sqrt{18}\) is incomplete.
- Misapplying Arithmetic Operations: When adding or subtracting radicals, ensure they have the same radicand. When multiplying, apply the property \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \times b}\). For example, \(\sqrt{6} \cdot \sqrt{3} = \sqrt{18}\), which simplifies to \(3\sqrt{2}\).
- Incorrectly Simplifying Radical Expressions: Pay attention to the properties of exponents and roots. For instance, \(\sqrt[3]{x^6}\) simplifies to \(x^2\) because \( \left(x^2\right)^3 = x^6 \).
- Ignoring Domain Restrictions: Ensure the radicand under an even root (e.g., square root) is non-negative. For example, \(\sqrt{-4}\) is not a real number.
Avoiding these mistakes will help you simplify radical expressions correctly and efficiently.

Practice Problems for Simplifying Radicals
Practicing simplifying radical expressions is essential for mastering the concepts. Below are several practice problems that cover a range of scenarios and difficulty levels. Work through each problem step-by-step, ensuring you follow the rules and methods discussed earlier.
Practice Problems
- Simplify: \( \sqrt{50} \)
- Simplify: \( \sqrt{72} \)
- Simplify: \( \sqrt[3]{27} \)
- Simplify: \( \sqrt{32} \)
- Simplify: \( \sqrt[4]{81} \)
- Simplify: \( \sqrt{45} \)
- Simplify: \( \sqrt[3]{64} \)
- Simplify: \( \sqrt{98} \)
Solutions
- \( \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2} \)
- \( \sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2} \)
- \( \sqrt[3]{27} = \sqrt[3]{3^3} = 3 \)
- \( \sqrt{32} = \sqrt{16 \cdot 2} = \sqrt{16} \cdot \sqrt{2} = 4\sqrt{2} \)
- \( \sqrt[4]{81} = \sqrt[4]{3^4} = 3 \)
- \( \sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5} \)
- \( \sqrt[3]{64} = \sqrt[3]{4^3} = 4 \)
- \( \sqrt{98} = \sqrt{49 \cdot 2} = \sqrt{49} \cdot \sqrt{2} = 7\sqrt{2} \)
By practicing these problems, you will improve your ability to simplify radical expressions quickly and accurately. Use these solutions to check your work and understand the steps involved in the simplification process.
Benefits of Simplifying Radical Expressions
Simplifying radical expressions offers several advantages that can aid in mathematical computations and understanding. Here are some key benefits:
- Ease of Computation: Simplified radicals are easier to work with, especially when performing arithmetic operations such as addition, subtraction, multiplication, and division.
- Clarity and Precision: Simplified expressions provide a clearer and more precise representation of the value, which is particularly useful in mathematical proofs and problem-solving.
- Identifying Properties: Simplifying radicals can help in recognizing properties of numbers and expressions, such as identifying perfect squares and cube roots.
- Simplification of Complex Problems: When dealing with complex problems, having simplified radicals makes it easier to manage and solve equations.
- Preparation for Higher Mathematics: Simplifying radicals is a fundamental skill required in advanced mathematics, including algebra, calculus, and beyond.
Let's consider a few examples to illustrate these benefits:
| Expression | Simplified Form | Benefit |
|---|---|---|
| \(\sqrt{50}\) | \(5\sqrt{2}\) | Makes it easier to handle in further calculations. |
| \(\sqrt{18} + \sqrt{8}\) | \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\) | Combining like terms simplifies the expression. |
| \(\sqrt{27}\) | \(3\sqrt{3}\) | Helps identify the factors of the radicand. |
By mastering the simplification of radicals, students and professionals can improve their mathematical proficiency and problem-solving capabilities, making it an invaluable skill in various fields of study and application.
Conclusion and Recap
In this comprehensive guide, we've delved into the fundamental concepts and techniques required to simplify radical expressions. Simplifying radicals is an essential skill in algebra that allows for easier manipulation and understanding of expressions involving roots.
Here's a brief recap of what we covered:
- Understanding Radical Expressions: We began with the basics, defining what radicals are and exploring their properties.
- Basic Rules for Simplifying Radicals: We discussed important rules such as combining like terms, using the product and quotient rules, and simplifying expressions involving higher roots.
- Methods for Simplifying Radicals: Detailed methods such as factorization and rationalizing the denominator were explained to help simplify more complex expressions.
- Using a Calculator: Various online calculators, such as those found on OmniCalculator, MathPortal, and CalculatorSoup, were introduced. These tools can simplify radicals efficiently by breaking down expressions into their simplest forms using prime factorization and other techniques.
- Step-by-Step Guide: A detailed, step-by-step approach was provided for manually simplifying radicals, ensuring a solid understanding of the process.
- Examples: Numerous examples demonstrated how to apply the methods learned, reinforcing the concepts and showing practical applications.
- Common Mistakes to Avoid: We highlighted frequent errors and misconceptions to watch out for, ensuring more accurate and confident problem-solving.
- Practice Problems: Practice problems were provided to test and reinforce the knowledge gained.
- Benefits: Finally, we discussed the advantages of simplifying radical expressions, such as making calculations more manageable and enhancing algebraic problem-solving skills.
Utilizing tools like the OmniCalculator, MathPortal, and CalculatorSoup can greatly aid in the simplification process, providing quick and accurate results. Whether you are adding, subtracting, multiplying, or dividing radicals, these calculators follow the arithmetic rules and simplify the expressions step-by-step, ensuring you understand each part of the process.
We hope this guide has been helpful in your journey to mastering the simplification of radical expressions. Remember, practice and familiarity with the rules and methods are key to becoming proficient. Happy calculating!
Hướng dẫn sử dụng máy tính ClassWiz để đơn giản hóa biểu thức căn. Video này sẽ giúp bạn làm quen với các chức năng của máy tính ClassWiz trong việc giải các bài toán liên quan đến biểu thức căn.
Hướng dẫn sử dụng máy tính ClassWiz - Đại số 4-1 Đơn giản hóa biểu thức căn
READ MORE:
Video này hướng dẫn cách đơn giản hóa biểu thức căn một cách chi tiết và dễ hiểu. Học cách sử dụng các phương pháp và công cụ để đơn giản hóa các biểu thức căn nhanh chóng và chính xác.
Đơn Giản Hóa Biểu Thức Căn













