Topic simplify square root 98: Unlock the secrets of simplifying the square root of 98 with our comprehensive guide. Whether you're a student or a math enthusiast, we'll take you through each step to simplify √98 effortlessly. Discover how understanding prime factorization and square roots can make math easier and more enjoyable.
Table of Content
- Simplifying the Square Root of 98
- Introduction to Simplifying Square Roots
- Understanding Square Roots and Their Properties
- Prime Factorization of 98
- Steps to Simplify the Square Root of 98
- Detailed Example: Simplifying √98
- General Steps to Simplify Square Roots
- Common Mistakes to Avoid in Simplification
- Applications of Simplified Square Roots in Math Problems
- Practice Problems: Simplifying Square Roots
- Conclusion and Summary of Key Points
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 98 một cách dễ hiểu và chi tiết.
Simplifying the Square Root of 98
Simplifying the square root of 98 involves breaking down the number into its prime factors and simplifying any square roots of perfect squares.
Step-by-Step Simplification Process:
- Identify the prime factors of 98.
- Break 98 down into its prime factors: \( 98 = 2 \times 7 \times 7 \).
- Group the prime factors into pairs of the same number: \( 98 = 2 \times (7 \times 7) \).
- Take the square root of each group: \( \sqrt{98} = \sqrt{2 \times 7^2} \).
- Simplify the square root: \( \sqrt{98} = \sqrt{2} \times \sqrt{7^2} \).
- Simplify further, knowing that \( \sqrt{7^2} = 7 \): \( \sqrt{98} = 7 \times \sqrt{2} \).
Final Simplified Form:
Therefore, the simplified form of \( \sqrt{98} \) is:
\( \sqrt{98} = 7 \sqrt{2} \)
Verification:
To verify, we can square the simplified result to ensure it matches the original number:
\( (7 \sqrt{2})^2 = 7^2 \times (\sqrt{2})^2 = 49 \times 2 = 98 \)
The verification confirms that our simplified form is correct.

READ MORE:
Introduction to Simplifying Square Roots
Square roots can often be simplified to make calculations easier. Simplifying a square root means expressing it in its simplest radical form. The process involves breaking down the number inside the square root into its prime factors and then pairing these factors to move them outside the radical.
Here are the basic steps to simplify a square root:
- Prime Factorization: Find the prime factors of the number under the square root.
- Pairing Factors: Group the prime factors into pairs.
- Moving Out of the Radical: For each pair of prime factors, one factor can be moved outside the square root.
- Multiplication: Multiply the factors outside the square root to get the simplified form.
Let's take an example:
Simplifying √98
Step 1: Prime Factorization
First, we find the prime factors of 98:
98 = 2 × 7 × 7
Step 2: Pairing Factors
We group the prime factors into pairs:
98 = 2 × (7 × 7)
Step 3: Moving Out of the Radical
Each pair of 7s can be moved outside the square root:
√98 = √(2 × 7 × 7) = 7√2
So, the simplified form of √98 is 7√2.
This method can be used for any number to simplify its square root. It's important to always check if the number inside the square root can be factored further to ensure it is in its simplest form.
Understanding how to simplify square roots is essential in various mathematical applications, making complex problems more manageable and solutions more elegant.
Understanding Square Roots and Their Properties
The concept of square roots is fundamental in mathematics. A square root of a number \( n \) is a value \( r \) such that \( r^2 = n \). The square root symbol is \( \sqrt{} \), and the number inside this symbol is called the radicand.
For example, \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \). Not all numbers are perfect squares, meaning they do not have an integer as their square root. For instance, \( \sqrt{2} \) is an irrational number, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.
Square roots have several important properties:
- Product Property: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). For example, \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For instance, \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \).
- Square of a Square Root: \( (\sqrt{a})^2 = a \). For example, \( (\sqrt{5})^2 = 5 \).
- Adding and Subtracting Square Roots: Square roots can only be added or subtracted if they have the same radicand. For example, \( 2\sqrt{3} + 4\sqrt{3} = 6\sqrt{3} \).
Understanding these properties is essential for simplifying square roots and solving various mathematical problems involving radicals. In the next section, we will delve into the prime factorization of numbers to further simplify square roots.
Prime Factorization of 98
Prime factorization is a method used to express a number as a product of its prime factors. To simplify the square root of 98, we first need to perform the prime factorization of 98.
Let's start with the number 98:
- Begin by dividing 98 by the smallest prime number, which is 2:
- Next, factor 49. Since 49 is not divisible by 2, we move to the next smallest prime number, which is 7:
- Finally, 7 is already a prime number:
98 ÷ 2 = 49
49 ÷ 7 = 7
7 ÷ 7 = 1
So, the prime factorization of 98 is:
\(98 = 2 \times 7 \times 7\) or \(98 = 2 \times 7^2\).
Using this factorization, we can simplify the square root of 98:
\(\sqrt{98} = \sqrt{2 \times 7^2}\)
We know that the square root of a product is the product of the square roots:
\(\sqrt{2 \times 7^2} = \sqrt{2} \times \sqrt{7^2}\)
Since the square root of \(7^2\) is 7:
\(\sqrt{2} \times \sqrt{7^2} = 7 \sqrt{2}\)
Therefore, the simplified form of \(\sqrt{98}\) is:
\(\boxed{7 \sqrt{2}}\)
Steps to Simplify the Square Root of 98
Simplifying the square root of 98 involves several clear steps. Follow these steps to express √98 in its simplest radical form:
-
Prime Factorization: Break down 98 into its prime factors.
98 can be written as:
98 = 2 × 49
Since 49 is also a product of prime numbers, we further break it down:
49 = 7 × 7
Therefore, 98 = 2 × 7 × 7
-
Group the Prime Factors: Look for pairs of prime numbers.
In 98, the prime factors are 2, 7, and 7. We can group the two 7s together:
98 = 2 × (7 × 7)
-
Extract the Square Root: For each pair of identical factors, take one factor out of the square root.
√98 = √(2 × 7 × 7)
√98 = 7√2
We have extracted a 7, leaving us with 7√2.
-
Conclusion: The simplified form of √98 is:
√98 = 7√2
Thus, the simplest radical form of the square root of 98 is 7√2.
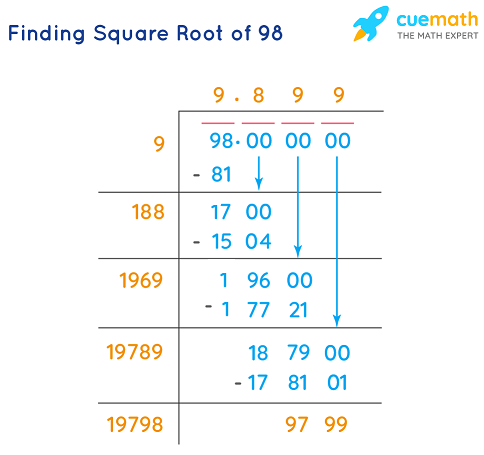
Detailed Example: Simplifying √98
Simplifying the square root of 98 involves expressing it in its simplest radical form. Follow these detailed steps to simplify √98:
-
Factorize 98 into its prime factors:
- 98 = 2 × 49
- 49 is a perfect square (72), so 98 = 2 × 72
-
Rewrite the square root of 98 using these factors:
√98 = √(2 × 72)
-
Separate the perfect square from the other factors:
√(2 × 72) = √(72) × √2
-
Simplify the square root of the perfect square:
√(72) = 7
-
Combine the simplified terms:
7 × √2
-
Thus, the simplified form of √98 is:
7√2
In summary, √98 simplifies to 7√2. This form is easier to work with in mathematical problems and is particularly useful in algebraic expressions.
For a deeper understanding and more practice, refer to online resources and problem sets to reinforce these concepts.
General Steps to Simplify Square Roots
Simplifying square roots involves reducing the expression inside the radical to its simplest form. Here are the general steps to simplify square roots:
-
Find the Prime Factorization:
Break down the number inside the square root into its prime factors. For example, for √98, the prime factorization is 2 and 72:
98 = 2 × 7 × 7
-
Group the Factors:
Group the prime factors into pairs. Each pair of the same number can be taken out of the radical as a single number. For √98, we have:
√(2 × 7 × 7) = √(72 × 2)
-
Simplify the Radical:
For each pair, take one factor out of the radical. If there are any factors that do not form a pair, they remain inside the radical. Using our example:
√(72 × 2) = 7√2
-
Final Simplified Form:
The simplified form of the square root is obtained by multiplying the numbers taken out of the radical. For √98, the simplified form is:
7√2
By following these steps, you can simplify any square root. Practice with different numbers to become more comfortable with the process.
Common Mistakes to Avoid in Simplification
When simplifying square roots, there are several common mistakes that can lead to incorrect results. Here are some key errors to watch out for and tips on how to avoid them:
- Ignoring the Prime Factorization Step: Skipping prime factorization can lead to incomplete simplification or incorrect results. Always factor the radicand fully to ensure accurate simplification.
- Misidentifying Perfect Squares: Confusing perfect and non-perfect squares can drastically affect the simplification process. Ensure you accurately recognize perfect squares within the radicand.
- Incorrectly Simplifying Variables: When dealing with square roots that include variables, it's important to apply the rules for variables correctly. For instance, remember that the square root of a variable raised to an even power is the variable raised to half that power (e.g., √x² = x).
- Overlooking Rationalization: Failing to rationalize the denominator when needed is a common oversight. Always rationalize to remove square roots from the denominator by multiplying the numerator and denominator by the square root in the denominator.
- Miscalculating with Non-Perfect Squares: Using approximation for non-perfect squares without proper verification can lead to inaccuracies. Always verify your final answers, especially when approximations are involved.
- Forgetting the Absolute Value: When variables are involved, forgetting to include absolute value signs when necessary can change the meaning of the solution. Ensure you account for absolute values to maintain the correctness of the expression.
By being mindful of these common errors and applying careful simplification strategies, you can enhance your proficiency in dealing with square roots.
Applications of Simplified Square Roots in Math Problems
Simplified square roots are not only a fundamental mathematical concept but also have numerous practical applications across various fields. Here are some key areas where simplified square roots are commonly used:
- Geometry and Trigonometry: Simplified square roots help in calculating the lengths of sides in geometric shapes, such as finding the hypotenuse in right-angled triangles using the Pythagorean theorem.
- Algebra: Simplifying square roots is crucial for solving quadratic equations and other algebraic expressions, making them easier to handle and solve.
- Physics: Square roots are used to calculate various physical quantities, such as the root mean square speed of gas molecules in thermodynamics or the magnitude of vectors in mechanics.
- Engineering: Engineers use simplified square roots to determine dimensions and tolerances in construction and manufacturing processes, ensuring accuracy and precision.
- Statistics: In statistics, square roots are used to calculate standard deviation and variance, which measure the spread of data points in a dataset.
- Finance: Financial analysts use square roots to compute the volatility of stock prices and other financial metrics, helping assess risk and make informed investment decisions.
- Computer Graphics: Simplified square roots are employed in computer graphics to calculate distances between points, magnitudes of vectors, and other geometric transformations.
- Architecture: Architects use square roots to determine the lengths of diagonal braces and other structural elements, ensuring the stability and integrity of buildings.
Overall, understanding how to simplify square roots is essential for tackling a wide range of mathematical problems and real-world applications efficiently and effectively.

Practice Problems: Simplifying Square Roots
Practicing the simplification of square roots helps reinforce understanding and improve proficiency. Below are a series of practice problems to help you master this skill. Work through each problem step by step, ensuring you follow the general steps to simplify square roots:
-
Problem 1: Simplify √50
Step-by-Step Solution:
- Prime Factorization: 50 = 2 × 5 × 5
- Group Factors: √(2 × 5²)
- Simplify: 5√2
-
Problem 2: Simplify √72
Step-by-Step Solution:
- Prime Factorization: 72 = 2 × 2 × 2 × 3 × 3
- Group Factors: √(2² × 2 × 3²)
- Simplify: 6√2
-
Problem 3: Simplify √98
Step-by-Step Solution:
- Prime Factorization: 98 = 2 × 7 × 7
- Group Factors: √(2 × 7²)
- Simplify: 7√2
-
Problem 4: Simplify √45
Step-by-Step Solution:
- Prime Factorization: 45 = 3 × 3 × 5
- Group Factors: √(3² × 5)
- Simplify: 3√5
-
Problem 5: Simplify √200
Step-by-Step Solution:
- Prime Factorization: 200 = 2 × 2 × 2 × 5 × 5
- Group Factors: √(2² × 5² × 2)
- Simplify: 10√2
By regularly practicing these problems, you will develop a stronger understanding of simplifying square roots and be better prepared to tackle more complex mathematical challenges.
Conclusion and Summary of Key Points
Simplifying square roots is a crucial skill in mathematics that helps in various problem-solving scenarios. Understanding the steps and avoiding common mistakes can make the process straightforward and efficient. Here are the key points covered:
- Prime Factorization: Break down the number into its prime factors and pair them to simplify the square root.
- Perfect Squares: Identify and use the largest perfect square factor to reduce the radicand effectively.
- Quotient Property: For fractions, simplify the numerator and denominator separately using the quotient property of square roots.
- Common Mistakes: Avoid errors such as not fully simplifying the radicand or incorrectly grouping prime factors.
- Applications: Simplified square roots are used in various mathematical contexts, including solving equations and working with geometric formulas.
- Practice: Regular practice with a variety of problems ensures proficiency in simplifying square roots.
By mastering these concepts, students can handle square roots confidently and apply these techniques to broader mathematical problems.
Hướng dẫn cách đơn giản hóa căn bậc hai của 98 một cách dễ hiểu và chi tiết.
Cách Đơn Giản Hóa Căn Bậc Hai Của 98: sqrt(98)
READ MORE:
Khám phá cách tính căn bậc hai của 98 và cách đơn giản hóa căn bậc hai này.
Căn Bậc Hai Của 98 | Căn 98







