Topic simplify square root 28: Understanding how to simplify the square root of 28 is essential for mastering algebra and higher-level math. This comprehensive guide breaks down the process into simple, easy-to-follow steps, ensuring you grasp the concept quickly and effectively. Whether you're a student or just refreshing your skills, you'll find this explanation straightforward and helpful.
Table of Content
- Simplifying the Square Root of 28
- Introduction to Simplifying Square Roots
- Understanding Square Roots
- Prime Factorization Method
- Step-by-Step Simplification of Square Root of 28
- Grouping Prime Factors
- Taking Square Roots of Pairs
- Expressing the Simplified Form
- Examples of Other Square Root Simplifications
- Common Mistakes to Avoid
- Applications of Simplified Square Roots
- Practice Problems
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 28, giúp bạn hiểu rõ hơn về phương pháp này.
Simplifying the Square Root of 28
The square root of 28 can be simplified by finding its prime factorization and grouping the factors into pairs.
Step-by-Step Process
- Find the prime factors of 28:
- 28 can be divided by 2 to give 14.
- 14 can be divided by 2 to give 7.
- 7 is a prime number.
- Express 28 as a product of its prime factors:
\( 28 = 2 \times 2 \times 7 \)
- Group the factors into pairs:
\( 28 = (2 \times 2) \times 7 \)
- Simplify the square root by taking the square root of each pair:
\( \sqrt{28} = \sqrt{(2 \times 2) \times 7} = \sqrt{2^2 \times 7} = 2\sqrt{7} \)
Final Simplified Form
The simplified form of \( \sqrt{28} \) is \( 2\sqrt{7} \).
READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in algebra that helps make complex expressions more manageable. When simplifying a square root, the goal is to express it in the simplest form possible. This involves finding the prime factors of the number under the square root and using the properties of square roots to simplify the expression.
Step-by-Step Process
- Understand the basic concept:
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
- Find the prime factorization:
Breaking down the number inside the square root into its prime factors helps in simplifying the expression. For example, \( 28 \) can be factorized into \( 2 \times 2 \times 7 \).
- Group the factors into pairs:
Identify pairs of prime factors. For \( 28 \), the factor pairs are \( (2 \times 2) \) and \( 7 \).
- Simplify using the properties of square roots:
Use the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) to simplify the expression. For example, \( \sqrt{28} = \sqrt{(2 \times 2) \times 7} = \sqrt{2^2 \times 7} = 2\sqrt{7} \).
By following these steps, you can simplify the square root of any number, making it easier to work with in various mathematical problems.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). Square roots are fundamental in mathematics and appear in various contexts, including geometry, algebra, and real-world applications.
Square roots can be expressed using the radical symbol \(\sqrt{}\). For example, the square root of 28 is written as \(\sqrt{28}\). When the square root of a number is an integer, it is called a perfect square. However, not all numbers are perfect squares, and their square roots are irrational numbers.
Let's understand square roots better with a few examples:
- \(\sqrt{1} = 1\) because \(1 \times 1 = 1\)
- \(\sqrt{4} = 2\) because \(2 \times 2 = 4\)
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\)
- \(\sqrt{16} = 4\) because \(4 \times 4 = 16\)
For non-perfect squares, the square root can often be simplified by finding the prime factors of the number and then grouping them. Simplifying the square root of a number like 28 involves breaking it down into its prime factors.
In summary, square roots are a way of finding the original value that was squared to produce a given number. They are an essential part of mathematics and have numerous applications in different fields.
Prime Factorization Method
The prime factorization method is an effective way to simplify square roots by breaking down the number into its prime factors. Here is a step-by-step guide to simplifying the square root of 28 using this method:
-
Find the prime factors of 28. The prime factors of 28 are 2 and 7.
So, we can express 28 as a product of its prime factors:
\[28 = 2 \times 2 \times 7\]
-
Group the prime factors into pairs. Each pair of the same number represents a square number:
\[28 = (2 \times 2) \times 7\]
-
Take the square root of each group. For the pair of 2's, the square root of \(2 \times 2\) is 2. The 7 remains under the square root since it does not have a pair:
\[\sqrt{28} = \sqrt{(2 \times 2) \times 7} = \sqrt{2^2 \times 7}\]
-
Separate the square root into two parts and simplify:
\[\sqrt{28} = \sqrt{2^2} \times \sqrt{7} = 2 \times \sqrt{7}\]
Therefore, the simplified form of the square root of 28 is:
\[\sqrt{28} = 2\sqrt{7}\]
This process can be used for any number to find its simplified square root using prime factorization.
Step-by-Step Simplification of Square Root of 28
Simplifying the square root of 28 involves breaking down the number into its prime factors and then simplifying the expression. Here is a step-by-step guide to help you understand the process:
-
List the factors of 28:
The factors of 28 are: 1, 2, 4, 7, 14, and 28.
-
Identify the perfect squares:
From the list of factors, identify the perfect squares. The perfect squares in the list are 1 and 4.
-
Divide by the largest perfect square:
Divide 28 by the largest perfect square identified in the previous step:
\[
\frac{28}{4} = 7
\] -
Calculate the square root of the perfect square:
The square root of 4 is 2:
\[
\sqrt{4} = 2
\] -
Simplify the expression:
Combine the results from the previous steps to get the simplified form of the square root of 28:
\[
\sqrt{28} = \sqrt{4 \times 7} = \sqrt{4} \times \sqrt{7} = 2 \sqrt{7}
\]Therefore, the simplified form of \(\sqrt{28}\) is \(2 \sqrt{7}\).

Grouping Prime Factors
To simplify the square root of 28, we need to use the prime factorization method. This involves breaking down the number 28 into its prime factors and then grouping these factors to simplify the square root. Let's go through the steps:
- Prime Factorization:
First, we find the prime factors of 28. We can write 28 as the product of its prime factors:
\( 28 = 2 \times 2 \times 7 \)
- Grouping the Factors:
Next, we group the prime factors in pairs. Since we have two 2's, we can form one pair of 2's:
\( 28 = 2^2 \times 7 \)
- Simplifying the Radical:
We take the square root of each group of pairs. For each pair of the same number, one number comes out of the square root:
\( \sqrt{28} = \sqrt{2^2 \times 7} \)
Since \(\sqrt{2^2} = 2\), we can simplify this further:
\( \sqrt{28} = 2 \sqrt{7} \)
Thus, the simplified form of the square root of 28 is \( 2 \sqrt{7} \). This process of grouping the prime factors allows us to simplify the square root efficiently.
Taking Square Roots of Pairs
To simplify the square root of 28, we need to take the square roots of pairs of prime factors. We have already grouped the prime factors in the previous step. Now, let's see how we can proceed with this step.
-
From the prime factorization of 28, we have identified that \( 28 = 2 \times 2 \times 7 \).
-
Next, we group the pairs of prime factors. In our case, we have one pair of 2s.
- \( 2 \times 2 = 2^2 \)
-
We can now take the square root of each pair of prime factors.
- \( \sqrt{2^2} = 2 \)
-
The remaining factor under the square root is 7.
- \( \sqrt{7} \) stays as it is because 7 is not a perfect square and does not have any pairs.
-
Putting it all together, we have:
- \( \sqrt{28} = \sqrt{2^2 \times 7} = 2 \sqrt{7} \)
Therefore, by taking the square roots of the pairs of prime factors and combining them with the remaining factors under the square root, we can express the simplified form of \( \sqrt{28} \) as \( 2 \sqrt{7} \).
Expressing the Simplified Form
After grouping the prime factors, we proceed to express the simplified form of the square root of 28.
Recall the prime factorization of 28: \( 28 = 2 \times 2 \times 7 \).
We have identified that \( \sqrt{28} = \sqrt{2 \times 2 \times 7} \).
To simplify, we take the square root of the pairs of prime factors. In this case, we have a pair of 2s.
The square root of \( 2 \times 2 \) is 2. This means that \( \sqrt{2 \times 2} = 2 \).
We are left with the square root of 7 under the radical sign: \( \sqrt{7} \).
Combining these results, we express the simplified form of \( \sqrt{28} \) as \( 2\sqrt{7} \).
Thus, the simplest radical form of the square root of 28 is \( 2\sqrt{7} \).
Examples of Other Square Root Simplifications
In this section, we will look at a few examples of simplifying other square roots to illustrate the process and highlight common techniques. These examples will help you apply the principles discussed so far to various scenarios.
Example 1: Simplifying \(\sqrt{50}\)
- Factor the radicand into prime factors: \(50 = 2 \times 5 \times 5\).
- Group the prime factors into pairs: \(50 = (5 \times 5) \times 2\).
- Take the square root of the pairs: \(\sqrt{50} = 5\sqrt{2}\).
Thus, the simplified form of \(\sqrt{50}\) is \(5\sqrt{2}\).
Example 2: Simplifying \(\sqrt{72}\)
- Factor the radicand into prime factors: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
- Group the prime factors into pairs: \(72 = (2 \times 2) \times (3 \times 3) \times 2\).
- Take the square root of the pairs: \(\sqrt{72} = 2 \times 3 \sqrt{2} = 6\sqrt{2}\).
Thus, the simplified form of \(\sqrt{72}\) is \(6\sqrt{2}\).
Example 3: Simplifying \(\sqrt{128}\)
- Factor the radicand into prime factors: \(128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\).
- Group the prime factors into pairs: \(128 = (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2\).
- Take the square root of the pairs: \(\sqrt{128} = 2 \times 2 \times 2 \sqrt{2} = 8\sqrt{2}\).
Thus, the simplified form of \(\sqrt{128}\) is \(8\sqrt{2}\).
Example 4: Simplifying \(\sqrt{75}\)
- Factor the radicand into prime factors: \(75 = 3 \times 5 \times 5\).
- Group the prime factors into pairs: \(75 = (5 \times 5) \times 3\).
- Take the square root of the pairs: \(\sqrt{75} = 5\sqrt{3}\).
Thus, the simplified form of \(\sqrt{75}\) is \(5\sqrt{3}\).
Example 5: Simplifying \(\sqrt{200}\)
- Factor the radicand into prime factors: \(200 = 2 \times 2 \times 2 \times 5 \times 5\).
- Group the prime factors into pairs: \(200 = (2 \times 2) \times (5 \times 5) \times 2\).
- Take the square root of the pairs: \(\sqrt{200} = 2 \times 5 \sqrt{2} = 10\sqrt{2}\).
Thus, the simplified form of \(\sqrt{200}\) is \(10\sqrt{2}\).
By practicing these examples, you can become more proficient at recognizing patterns and applying the steps to simplify any square root expression.

Common Mistakes to Avoid
When simplifying square roots, there are several common mistakes that students often make. Avoiding these errors can make the process smoother and more accurate:
- Forgetting to Check for Perfect Squares: Before simplifying, always check if the number under the square root is a perfect square. If it is, the simplification is straightforward.
- Rushing Through the Process: Simplifying square roots requires careful step-by-step execution. Taking your time to ensure each step is done correctly is essential.
- Incorrect Prime Factorization: Make sure to accurately factorize the number into its prime factors. Any mistake in this step will lead to incorrect simplification.
- Misunderstanding the Properties of Radicals: Remember that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) only holds if both \(a\) and \(b\) are non-negative. For negative numbers, this property does not apply.
- Overlooking Pairs of Factors: Ensure that pairs of prime factors are correctly identified and moved outside the square root as a single factor. For instance, in \(\sqrt{28}\), the factor pair \((2, 2)\) should be simplified to 2 outside the square root.
- Ignoring the Negative Square Root: When solving equations involving square roots, remember that both positive and negative roots should be considered. For example, \(x^2 = 9\) leads to \(x = \pm 3\).
- Incorrectly Simplifying Expressions: Be cautious when simplifying expressions that involve addition or subtraction under the square root. For example, \(\sqrt{x^2 + y^2} \neq x + y\).
By being aware of these common mistakes and taking care to avoid them, you can ensure that your simplification process is accurate and effective.
Applications of Simplified Square Roots
Simplified square roots have numerous applications in various fields such as mathematics, physics, engineering, and even in daily life. Here are some common uses:
- Geometry: Simplified square roots are often used to find the lengths of sides in right triangles (using the Pythagorean theorem), areas of squares and rectangles, and in calculations involving circles and other shapes.
- Physics: In physics, square roots appear in formulas for wave functions, kinetic energy, and other equations involving quadratic relationships. Simplifying these roots can make calculations more straightforward.
- Engineering: Engineers use simplified square roots in designing structures, analyzing forces, and solving problems related to stress and strain. For example, the stress on a beam can involve square root calculations that need simplification for clarity and accuracy.
- Finance: In finance, the calculation of standard deviation and variance, which are crucial in risk assessment and investment strategies, often involves the simplification of square roots.
- Daily Life: Simplified square roots can help in practical situations like determining dimensions for home projects, cooking recipes that involve area and volume measurements, or even in navigation where distance needs to be calculated precisely.
These examples illustrate the importance of understanding and being able to simplify square roots efficiently, as it aids in problem-solving and enhances accuracy in various practical and theoretical applications.
Practice Problems
Here are some practice problems to help you master the process of simplifying square roots:
- Simplify the square root of 50:
\[\sqrt{50} = \sqrt{2 \times 5 \times 5} = 5\sqrt{2}\]
- Simplify the square root of 72:
\[\sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} = 6\sqrt{2}\]
- Simplify the square root of 98:
\[\sqrt{98} = \sqrt{2 \times 7 \times 7} = 7\sqrt{2}\]
- Simplify the square root of 128:
\[\sqrt{128} = \sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2} = 8\sqrt{2}\]
- Simplify the square root of 180:
\[\sqrt{180} = \sqrt{2 \times 2 \times 3 \times 3 \times 5} = 6\sqrt{5}\]
By practicing these problems, you will become more comfortable with the steps involved in simplifying square roots. Remember to look for pairs of prime factors and simplify accordingly.
Conclusion
Simplifying square roots, such as the square root of 28, is a fundamental skill in mathematics that helps in various applications, from solving equations to understanding geometric properties. By breaking down a number into its prime factors and grouping them, we can express square roots in their simplest form. This process not only makes calculations easier but also deepens our understanding of number properties.
To summarize, the steps to simplify the square root of 28 involve:
- Finding the prime factors of 28, which are 2 and 7.
- Grouping the prime factors into pairs.
- Taking the square root of the pairs and expressing the simplified form.
We demonstrated that , showing that the simplified form of the square root of 28 is . This process is not limited to 28 but can be applied to any number to find its simplest square root form.
By practicing this method, you can enhance your mathematical skills and improve your ability to tackle more complex problems. Always remember to check your work to avoid common mistakes, such as missing a factor or incorrect grouping. With these tools, simplifying square roots becomes a straightforward and valuable part of your mathematical toolkit.
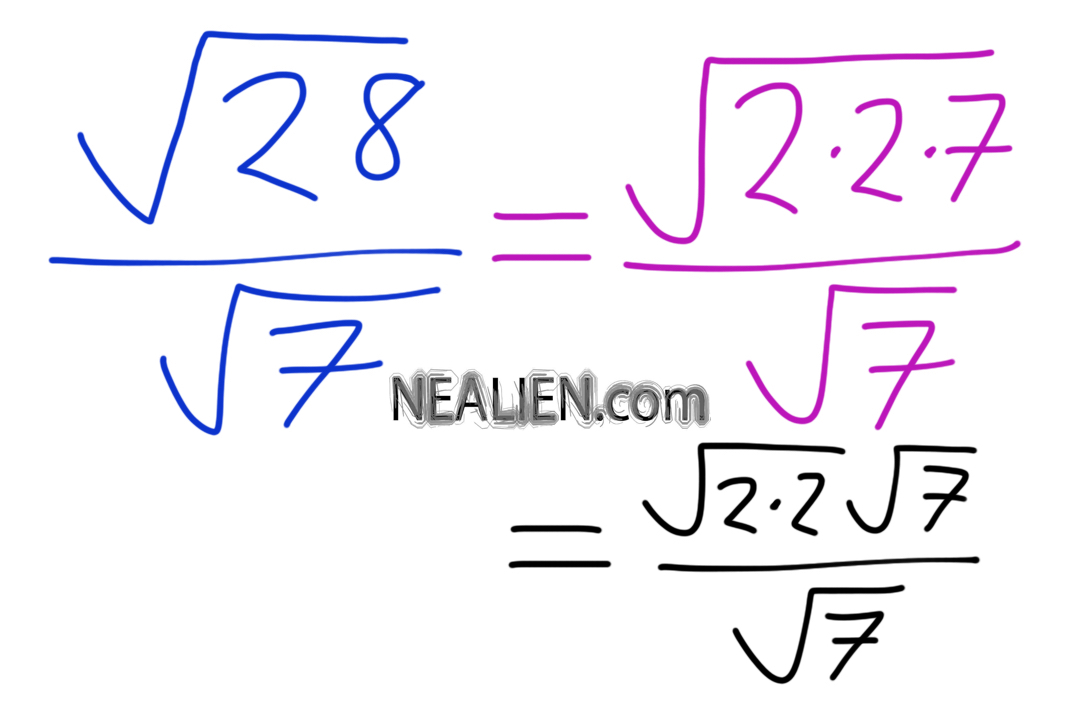
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 28, giúp bạn hiểu rõ hơn về phương pháp này.
Cách Đơn Giản Hóa Căn Bậc Hai Của 28: Sqrt(28)
READ MORE:
Hợp nhất căn bậc hai: Giản đơn √(28)
Hợp nhất căn bậc hai: Giản đơn √(28)






