Simplify Square Root 128: Step-by-Step Guide

Simplifying the square root of a number involves finding the prime factorization of the number and then simplifying the radical by pairing the prime factors. Here's a step-by-step guide to simplify the square root of 128.

Step 1: Find the Prime Factorization of 128

First, we need to find the prime factors of 128. We can do this by continuously dividing by the smallest prime number until we reach 1.

• 128 ÷ 2 = 64
• 64 ÷ 2 = 32
• 32 ÷ 2 = 16
• 16 ÷ 2 = 8
• 8 ÷ 2 = 4
• 4 ÷ 2 = 2

Therefore, the prime factorization of 128 is:

\(128 = 2^7\)

Step 2: Pair the Prime Factors

Next, we pair the prime factors to simplify the radical. For every pair of prime factors, we can take one factor out of the square root.

\(128 = 2^7 = (2^3)^2 \times 2 = (8)^2 \times 2\)

Step 3: Simplify the Square Root

We can now simplify the square root by taking the square root of the pairs and multiplying it by the remaining factors inside the radical.

\(\sqrt{128} = \sqrt{(8)^2 \times 2} = 8 \sqrt{2}\)

Final Result

The simplified form of \(\sqrt{128}\) is:

\[\sqrt{128} = 8\sqrt{2}\]

Understanding how to simplify square roots is essential in mathematics. Simplifying the square root of a number means breaking it down into its simplest form. For example, the square root of 128 can be simplified by using the prime factorization method. This involves finding the prime factors of 128 and then grouping them to simplify the expression. Let's dive into the steps for simplifying square roots.

The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 multiplied by 3 equals 9. Square roots are typically represented by the radical symbol (√). For instance, the square root of 128 is written as √128.

Understanding square roots involves knowing a few key properties:

• Perfect Squares: These are numbers whose square roots are whole numbers. Examples include 1, 4, 9, 16, 25, etc. For example, √16 = 4.
• Non-Perfect Squares: These are numbers whose square roots are not whole numbers, often resulting in irrational numbers. An example is √2, which is approximately 1.414.

The square root function is the inverse operation of squaring a number. If you square a number and then take the square root, you return to the original number.

Here are some rules and properties of square roots:

• Product Property: The square root of a product is the product of the square roots. For example, √(a * b) = √a * √b. This is useful when simplifying square roots of larger numbers.
• Quotient Property: The square root of a quotient is the quotient of the square roots. For example, √(a / b) = √a / √b.
• Simplifying Square Roots: To simplify a square root, factor the number into its prime factors and pair the factors. For example, √128 can be simplified by finding its prime factorization: 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2, which simplifies to 8√2.

Simplifying square roots often involves breaking down a number into its prime factors and then grouping the factors into pairs. Here’s a step-by-step example:

1. Factor the number: Start with the number inside the radical and factor it into prime numbers. For 128, the prime factorization is 2 × 2 × 2 × 2 × 2 × 2 × 2.
2. Group the factors: Group the prime factors into pairs: (2 × 2), (2 × 2), and (2 × 2), with one 2 left over.
3. Extract the square roots: Take the square root of each pair. For each pair of 2's, the square root is 2, so √(2 × 2) = 2.
4. Simplify: Multiply the results outside the radical by the remaining factor inside. This gives us 2 × 2 × 2 × √2 = 8√2.

Therefore, the simplified form of √128 is 8√2. Understanding these basics helps in simplifying and working with square roots in various mathematical contexts.

The prime factorization method is an effective way to simplify the square root of a number by breaking it down into its prime factors and then simplifying the square root of the product of these factors. Here’s a detailed step-by-step guide to using the prime factorization method to simplify \(\sqrt{128}\).

1. Factorize the Number into Prime Factors:

   Start by dividing the number 128 by the smallest prime number, which is 2, and continue the process with the quotient until you reach 1.

   • 128 ÷ 2 = 64
   • 64 ÷ 2 = 32
   • 32 ÷ 2 = 16
   • 16 ÷ 2 = 8
   • 8 ÷ 2 = 4
   • 4 ÷ 2 = 2
   • 2 ÷ 2 = 1

   So, the prime factorization of 128 is \(2^7\) or \(2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\).

2. Organize the Prime Factors into Pairs:

   Group the prime factors into pairs of identical factors.

   \[
   128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2
   \]

   This can be simplified as:

   \[
   128 = (2^2) \times (2^2) \times (2^2) \times 2
   \]

3. Extract the Square Roots from the Pairs:

   Take one factor from each pair and place it outside the square root symbol. Any factor that does not have a pair remains under the square root.

   \[
   \sqrt{128} = \sqrt{(2^2) \times (2^2) \times (2^2) \times 2} = 2 \times 2 \times 2 \times \sqrt{2}
   \]

4. Multiply the Extracted Factors:

   Multiply the factors outside the square root to get the simplified form.

   \[
   2 \times 2 \times 2 = 8
   \]

   Therefore, \(\sqrt{128}\) simplifies to:

   \[
   \sqrt{128} = 8\sqrt{2}
   \]

This method can be applied to any number to find its simplified square root, especially when the number is not a perfect square.

Finding the prime factors of a number involves breaking it down into the set of prime numbers which, when multiplied together, result in the original number. For 128, this process can be done as follows:

1. Divide by the Smallest Prime Number:

   Start by dividing 128 by the smallest prime number, which is 2.

   • 128 ÷ 2 = 64
2. Continue Dividing by 2:

   Continue dividing the quotient by 2 until you cannot divide evenly by 2 anymore.

   • 64 ÷ 2 = 32
   • 32 ÷ 2 = 16
   • 16 ÷ 2 = 8
   • 8 ÷ 2 = 4
   • 4 ÷ 2 = 2
   • 2 ÷ 2 = 1
3. List All the Prime Factors:

   Since all these divisions resulted in whole numbers, the prime factors of 128 are all 2s. Therefore, 128 can be expressed as:

   \[
   128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^7
   \]

4. Check Your Work:

   To verify, you can multiply the prime factors together to ensure they equal the original number:

   \[
   2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 128
   \]

By following these steps, you can find that the prime factors of 128 are all 2s, and it can be written as \(2^7\).

After identifying the prime factors of 128, which are all 2s, the next step is to group these factors to simplify the square root. Here’s a detailed process for grouping the prime factors:

1. Write Down the Prime Factorization:

   The prime factorization of 128 is:

   \[
   128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^7
   \]

2. Group the Prime Factors in Pairs:

   To simplify the square root, group the factors in pairs of two:

   • \[ 2^7 = (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2 \]
   • This can be written as:
   • \[ 2^7 = 2^2 \times 2^2 \times 2^2 \times 2 \]
3. Take the Square Root of Each Pair:

   Since the square root of \(2^2\) is 2, extract 2 from each pair:

   • \[ \sqrt{2^2 \times 2^2 \times 2^2 \times 2} = 2 \times 2 \times 2 \times \sqrt{2} \]
   • Combine the extracted factors:
   • \[ 2 \times 2 \times 2 = 8 \]
4. Multiply the Extracted Factors:

   Combine the extracted factors and the remaining factor under the square root:

   • \[ \sqrt{128} = 8 \sqrt{2} \]

By grouping the prime factors of 128 and extracting the pairs, we simplify \(\sqrt{128}\) to \(8 \sqrt{2}\).

After grouping the prime factors, we can now extract the square roots from these groups. This process involves taking one number out of the square root for each pair of identical numbers inside the square root. Here's how you can do it:

1. Recall the prime factorization of 128: \(128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\). This can be grouped as \((2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2\).

2. Each pair of 2's will come out of the square root as a single 2, since \(\sqrt{a \times a} = a\).

3. We have three pairs of 2's: \((2 \times 2) \times (2 \times 2) \times (2 \times 2)\). Thus, for each pair, we take out a 2:

   \[
   \sqrt{(2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2} = 2 \times 2 \times 2 \times \sqrt{2} = 8\sqrt{2}
   \]

4. The simplified form of \(\sqrt{128}\) is therefore \(8\sqrt{2}\).

This method of grouping prime factors and extracting square roots can be applied to any number. Always look for pairs of factors to simplify the expression under the square root.

To simplify \(\sqrt{128}\), we will use the method of prime factorization and extracting square roots from groups of prime factors. Follow the steps below to simplify \(\sqrt{128}\):

1. Prime Factorization: First, we find the prime factors of 128. We repeatedly divide 128 by 2 (the smallest prime number) until we reach 1.

   • 128 ÷ 2 = 64
   • 64 ÷ 2 = 32
   • 32 ÷ 2 = 16
   • 16 ÷ 2 = 8
   • 8 ÷ 2 = 4
   • 4 ÷ 2 = 2
   • 2 ÷ 2 = 1

   So, the prime factors of 128 are: \(128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^7\).

2. Grouping Prime Factors: Next, we group the prime factors in pairs:

   \(2^7\) can be grouped as \((2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2\), which simplifies to \((2^2) \times (2^2) \times (2^2) \times 2\).

3. Extracting Square Roots: For each pair of \(2^2\), we can take the square root:

   \(\sqrt{(2^2)} = 2\)

   Since we have three pairs of \(2^2\), we can take out three 2's from under the square root:

   \(\sqrt{2^7} = \sqrt{(2^2 \times 2^2 \times 2^2 \times 2)} = 2 \times 2 \times 2 \times \sqrt{2} = 8\sqrt{2}\)

4. Final Simplified Form: Therefore, the simplified form of \(\sqrt{128}\) is:

   \(\sqrt{128} = 8\sqrt{2}\)

By following these steps, we have simplified the square root of 128 to its simplest form, \(8\sqrt{2}\).

Let's explore some additional examples of simplifying square roots using the prime factorization method. Each example will be broken down step by step to illustrate the process clearly.

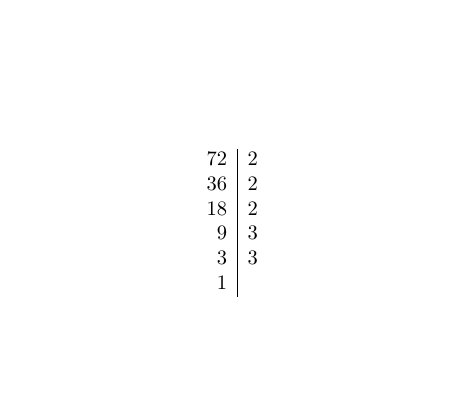
Example 1: Simplifying \(\sqrt{72}\)

1. Find the prime factors of 72:
   • 72 = 2 × 36
   • 36 = 2 × 18
   • 18 = 2 × 9
   • 9 = 3 × 3
   • So, 72 = 2 × 2 × 2 × 3 × 3
2. Group the prime factors into pairs:
   • (2 × 2), (2), (3 × 3)
3. Extract the square roots from the pairs:
   • 2 and 3 are extracted, leaving one 2 inside the square root.
4. Simplify:
   • \(\sqrt{72} = 2 × 3 × \sqrt{2} = 6\sqrt{2}\)

Example 2: Simplifying \(\sqrt{200}\)

1. Find the prime factors of 200:
   • 200 = 2 × 100
   • 100 = 2 × 50
   • 50 = 2 × 25
   • 25 = 5 × 5
   • So, 200 = 2 × 2 × 2 × 5 × 5
2. Group the prime factors into pairs:
   • (2 × 2), (5 × 5), (2)
3. Extract the square roots from the pairs:
   • 2 and 5 are extracted, leaving one 2 inside the square root.
4. Simplify:
   • \(\sqrt{200} = 2 × 5 × \sqrt{2} = 10\sqrt{2}\)

Example 3: Simplifying \(\sqrt{50}\)

1. Find the prime factors of 50:
   • 50 = 2 × 25
   • 25 = 5 × 5
   • So, 50 = 2 × 5 × 5
2. Group the prime factors into pairs:
   • (5 × 5), (2)
3. Extract the square roots from the pairs:
   • 5 is extracted, leaving one 2 inside the square root.
4. Simplify:
   • \(\sqrt{50} = 5\sqrt{2}\)

Example 4: Simplifying \(\sqrt{180}\)

1. Find the prime factors of 180:
   • 180 = 2 × 90
   • 90 = 2 × 45
   • 45 = 3 × 15
   • 15 = 3 × 5
   • So, 180 = 2 × 2 × 3 × 3 × 5
2. Group the prime factors into pairs:
   • (2 × 2), (3 × 3), (5)
3. Extract the square roots from the pairs:
   • 2 and 3 are extracted, leaving one 5 inside the square root.
4. Simplify:
   • \(\sqrt{180} = 2 × 3 × \sqrt{5} = 6\sqrt{5}\)

Simplifying square roots can sometimes lead to errors if not done carefully. Here are some common mistakes to avoid:

• Not checking for perfect squares: Always look for perfect square factors of the number under the square root. For example, in \(\sqrt{128}\), the perfect square factor is 64, since \(64 \times 2 = 128\).
• Skipping steps in prime factorization: Ensure you factorize the number completely. For \(\sqrt{128}\), the prime factorization is \(128 = 2^7\), which simplifies to \(8\sqrt{2}\).
• Incorrectly grouping factors: When simplifying, group factors in pairs. For instance, \(2^7\) should be grouped as \((2^6 \times 2)\) to extract the square root properly.
• Overlooking simplification of the radical: After factoring, always simplify the expression fully. For \(\sqrt{128}\), this means simplifying to \(8\sqrt{2}\), not leaving it as \(\sqrt{64 \times 2}\).
• Rushing through calculations: Take your time with each step to ensure accuracy. Verify each factorization and simplification carefully.

Avoiding these common mistakes will help ensure accurate and simplified square root expressions.

Simplified square roots are useful in various real-world applications. Here are some practical examples:

• Geometry and Construction: Square roots are essential in calculating distances, areas, and volumes. For example, when dealing with the dimensions of a square or rectangular plot of land, simplifying square roots can help in determining the lengths of diagonals.
• Physics: In physics, square roots appear in formulas for calculating forces, energy, and wave frequencies. For instance, the period of a pendulum is proportional to the square root of its length, making simplification crucial for accurate measurements.
• Engineering: Engineers often encounter square roots in stress-strain calculations, electrical circuits, and signal processing. Simplified square roots help streamline these complex calculations, ensuring precision and efficiency.
• Statistics: In statistics, the standard deviation, a measure of data dispersion, involves square roots. Simplifying square roots makes it easier to interpret and compare statistical results.
• Computer Science: Algorithms for graphics rendering, optimization problems, and data analysis frequently use square roots. Simplified forms improve the performance and accuracy of these algorithms.

By simplifying square roots, such as turning \(\sqrt{128}\) into \(8\sqrt{2}\), we make calculations more manageable and the results more comprehensible, enhancing their practical utility across various fields.

Simplifying square roots is a fundamental skill in mathematics that aids in various complex calculations. By breaking down a number like 128 into its prime factors and identifying the largest perfect square, we simplify the expression to its most concise form. This not only makes the calculation easier but also enhances our understanding of mathematical concepts.

Throughout this guide, we have explored the steps to simplify \(\sqrt{128}\) to \(8\sqrt{2}\), emphasizing the importance of prime factorization, correct grouping of factors, and careful simplification. We also highlighted common mistakes to avoid and discussed practical applications across different fields such as geometry, physics, engineering, statistics, and computer science.

Mastering the simplification of square roots enables us to tackle more advanced mathematical problems with confidence and precision. It ensures that we can apply these skills in real-world scenarios, making complex calculations more manageable and comprehensible.

By adhering to the outlined methods and being mindful of potential pitfalls, anyone can become proficient in simplifying square roots, thus enhancing their overall mathematical proficiency.