Topic simplifying square root expressions calculator: Discover the ease of using a simplifying square root expressions calculator to quickly and accurately simplify complex square roots. This powerful tool is perfect for students, educators, and professionals seeking efficient solutions. Learn how to streamline your calculations and enhance your mathematical understanding with step-by-step guides and practical examples.
Table of Content
- Simplifying Square Root Expressions Calculator
- Introduction to Simplifying Square Root Expressions
- Benefits of Using a Square Root Calculator
- How to Simplify Square Root Expressions Manually
- Step-by-Step Guide to Using an Online Calculator
- Examples of Simplified Square Root Expressions
- Advanced Techniques for Complex Expressions
- Common Mistakes to Avoid
- Applications of Simplified Square Roots in Real Life
- Frequently Asked Questions (FAQs)
- Additional Resources and Tools
- Conclusion and Final Tips
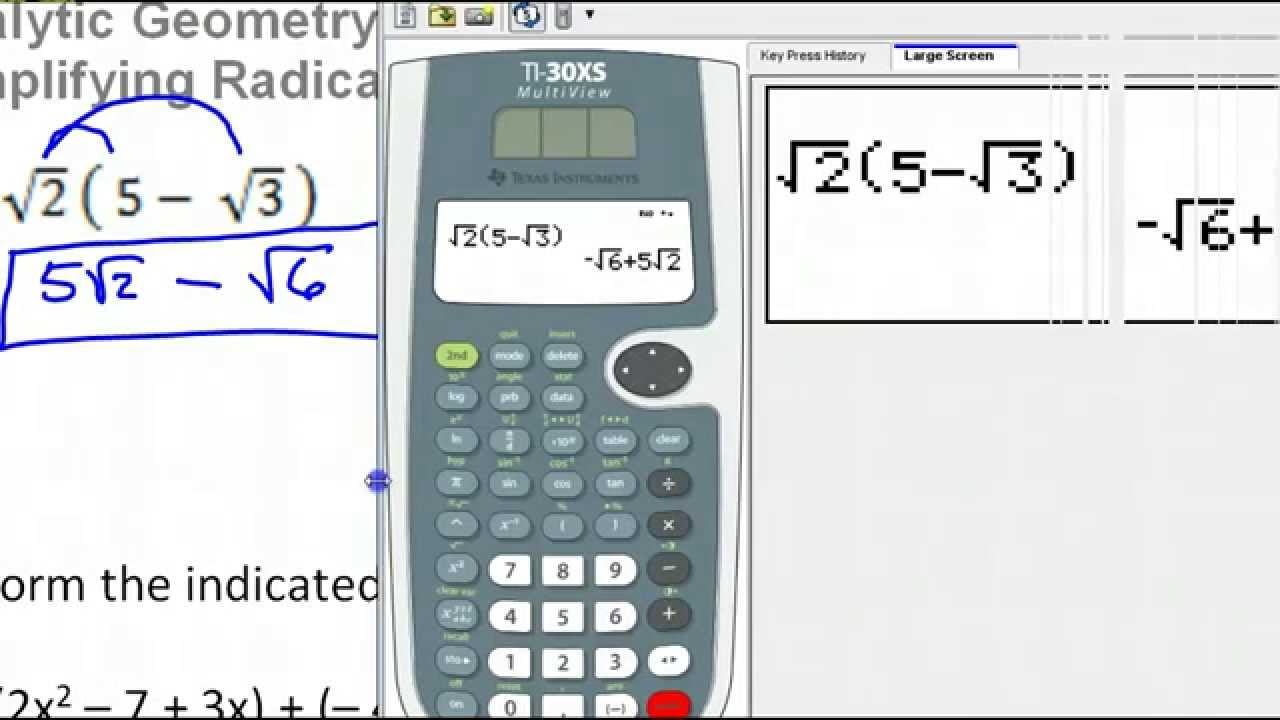
- YOUTUBE: Video hướng dẫn cách sử dụng máy tính TI-30xs mv để đơn giản hóa căn bậc hai. Phù hợp cho các bài toán đại số và học sinh chuẩn bị thi.
Simplifying Square Root Expressions Calculator
Simplifying square root expressions can be made easy with the use of online calculators. These tools help to break down complex square roots into their simplest forms. Below, we present some of the key features and benefits of using these calculators:
Key Features
- Step-by-Step Solutions: Many calculators provide detailed step-by-step solutions to help users understand the simplification process.
- Supports Complex Expressions: They can handle a variety of expressions, including those with variables and higher-order roots.
- Immediate Results: Instant simplification of square roots with just a few clicks.
- User-Friendly Interface: Easy-to-use interfaces that make the process straightforward even for beginners.
How to Use the Calculator
- Enter the square root expression you wish to simplify into the calculator.
- Click the "Simplify" button to process the expression.
- Review the step-by-step solution provided by the calculator.
- Use the simplified form in your calculations or further studies.
Example: Simplifying \( \sqrt{450} \)
Using a square root simplification calculator, you can simplify \( \sqrt{450} \) as follows:
- Enter the expression \( \sqrt{450} \).
- Click "Simplify" to get the result.
- The calculator will break down \( 450 \) into its prime factors: \( 450 = 2 \times 3^2 \times 5^2 \).
- Applying the square root, you get:
\( \sqrt{450} \) = \( \sqrt{2 \times 3^2 \times 5^2} \) = \( \sqrt{2} \times \sqrt{3^2} \times \sqrt{5^2} \) = \( \sqrt{2} \times 3 \times 5 \) = \( 15 \sqrt{2} \)
Therefore, \( \sqrt{450} = 15 \sqrt{2} \).
Conclusion
Square root simplification calculators are valuable tools for students and professionals alike. They simplify the process of breaking down complex expressions and provide clear, understandable steps. Whether you're working on homework, preparing for exams, or dealing with mathematical problems in your profession, these calculators can save time and enhance your understanding of square roots.

READ MORE:
Introduction to Simplifying Square Root Expressions
Simplifying square root expressions involves breaking down a square root into its simplest form. This process makes calculations easier and more understandable. A square root expression can often be simplified by identifying perfect square factors and reducing the expression to a simpler radical form.
Here are the steps to simplify square root expressions:
- Factor the Radicand: Break down the number inside the square root (the radicand) into its prime factors.
- Identify Perfect Squares: Look for pairs of prime factors, as these pairs can be taken out of the square root.
- Simplify the Expression: Rewrite the expression, moving any perfect squares outside the radical.
Consider the example of simplifying \( \sqrt{450} \):
- Factor the Radicand:
First, factorize 450 into prime factors:
- 450 = 2 × 3² × 5²
- Identify Perfect Squares:
Identify the perfect squares (3² and 5²) in the factorization:
- 3² and 5² are perfect squares.
- Simplify the Expression:
Rewrite the square root by extracting the perfect squares:
- \( \sqrt{450} = \sqrt{2 \times 3^2 \times 5^2} \)
- \( \sqrt{450} = \sqrt{2} \times \sqrt{3^2} \times \sqrt{5^2} \)
- \( \sqrt{450} = \sqrt{2} \times 3 \times 5 \)
- \( \sqrt{450} = 15 \sqrt{2} \)
Therefore, \( \sqrt{450} \) simplifies to \( 15 \sqrt{2} \). Using a simplifying square root expressions calculator can significantly speed up this process, providing accurate results and detailed steps for better understanding.
Benefits of Using a Square Root Calculator
Using a square root calculator offers numerous advantages, making it an invaluable tool for students, educators, and professionals alike. Here are the key benefits:
- Accuracy: Square root calculators provide precise and accurate results, minimizing the risk of human error in manual calculations.
- Speed: These calculators deliver instant results, saving time and effort compared to manual computations.
- Convenience: Online square root calculators are accessible from any device with an internet connection, allowing for easy and convenient calculations on the go.
- Step-by-Step Solutions: Many calculators offer detailed step-by-step solutions, helping users understand the process of simplifying square root expressions.
- Handling Complex Expressions: Advanced calculators can simplify complex square root expressions, including those involving variables and higher-order roots.
- Educational Aid: These tools are excellent for educational purposes, providing students with a clear understanding of mathematical concepts and aiding in homework and study sessions.
- Versatility: Square root calculators can be used for a wide range of applications, from simple arithmetic to advanced mathematical problems in various fields.
Consider the example of simplifying \( \sqrt{200} \) using a square root calculator:
- Enter the expression \( \sqrt{200} \) into the calculator.
- Click the "Simplify" button to process the expression.
- The calculator provides the simplified form:
- \( \sqrt{200} = \sqrt{2^3 \times 5^2} \)
- \( \sqrt{200} = \sqrt{2^3} \times \sqrt{5^2} \)
- \( \sqrt{200} = \sqrt{4 \times 50} = 2 \sqrt{50} = 2 \times 5 \sqrt{2} = 10 \sqrt{2} \)
This simplification process is made quick and easy with the use of a square root calculator, demonstrating the tool's effectiveness in breaking down and solving mathematical expressions efficiently.
How to Simplify Square Root Expressions Manually
Simplifying square root expressions manually involves breaking down the expression into its simplest form by identifying and extracting perfect square factors. Here’s a step-by-step guide to help you through the process:
- Identify the Radicand:
Determine the number inside the square root, known as the radicand. For example, in \( \sqrt{72} \), the radicand is 72.
- Factor the Radicand:
Break down the radicand into its prime factors. For 72, the prime factorization is:
- 72 = 2 × 2 × 2 × 3 × 3
- Group the Factors:
Group the prime factors into pairs of identical factors:
- 72 = (2 × 2) × (3 × 3) × 2
- Simplify by Extracting Pairs:
Extract each pair of identical factors out of the square root as a single factor:
- \( \sqrt{72} = \sqrt{(2 × 2) × (3 × 3) × 2} \)
- \( \sqrt{72} = 2 × 3 × \sqrt{2} \)
- \( \sqrt{72} = 6 \sqrt{2} \)
Therefore, \( \sqrt{72} \) simplifies to \( 6 \sqrt{2} \).
Here’s another example to further illustrate the process:
- Identify the Radicand:
Consider \( \sqrt{180} \). The radicand is 180.
- Factor the Radicand:
Break down 180 into its prime factors:
- 180 = 2 × 2 × 3 × 3 × 5
- Group the Factors:
Group the prime factors into pairs:
- 180 = (2 × 2) × (3 × 3) × 5
- Simplify by Extracting Pairs:
Extract each pair out of the square root:
- \( \sqrt{180} = \sqrt{(2 × 2) × (3 × 3) × 5} \)
- \( \sqrt{180} = 2 × 3 × \sqrt{5} \)
- \( \sqrt{180} = 6 \sqrt{5} \)
Therefore, \( \sqrt{180} \) simplifies to \( 6 \sqrt{5} \).
By following these steps, you can manually simplify any square root expression, making complex calculations more manageable and understandable.
Step-by-Step Guide to Using an Online Calculator
Using an online calculator to simplify square root expressions is a quick and efficient method. Here’s a detailed step-by-step guide to help you use these tools effectively:
- Access the Calculator:
Open your web browser and search for a reliable "simplifying square root expressions calculator". Select one from the search results.
- Enter the Expression:
Locate the input field on the calculator's page. Enter the square root expression you want to simplify. For example, if you want to simplify \( \sqrt{98} \), type "sqrt(98)" into the input field.
- Initiate the Calculation:
Click on the "Simplify" or "Calculate" button to process the expression. The calculator will automatically break down the expression into its simplest form.
- Review the Solution:
The calculator will display the simplified form of the expression. For example, it might show:
- \( \sqrt{98} = \sqrt{2 \times 7^2} = 7 \sqrt{2} \)
- View Step-by-Step Explanation:
Many online calculators provide a detailed step-by-step explanation of the simplification process. Review these steps to understand how the result was obtained:
- Factor the radicand: 98 = 2 × 7 × 7
- Group the factors: \( \sqrt{98} = \sqrt{2 \times 7^2} \)
- Extract the perfect square: \( \sqrt{98} = 7 \sqrt{2} \)
- Verify the Result:
Some calculators allow you to verify the result by entering additional expressions or performing further calculations. Utilize these features if needed to ensure accuracy.
- Practice with Additional Examples:
To gain confidence, practice simplifying other square root expressions using the calculator. Try expressions like \( \sqrt{50} \), \( \sqrt{75} \), and \( \sqrt{128} \) to see the process in action.
Using an online calculator to simplify square root expressions can save time and provide clarity, especially when dealing with complex numbers. These tools are designed to be user-friendly and offer accurate results, making them an essential resource for students, educators, and professionals.

Examples of Simplified Square Root Expressions
Simplifying square root expressions involves breaking down the radicand into its prime factors and simplifying the expression by extracting perfect squares. Here are some detailed examples to illustrate the process:
Example 1: Simplifying \( \sqrt{72} \)
- Factor the Radicand:
Break down 72 into its prime factors:
- 72 = 2 × 2 × 2 × 3 × 3
- Group the Factors:
Group the factors into pairs:
- 72 = (2 × 2) × (3 × 3) × 2
- Extract the Perfect Squares:
Extract each pair of factors from under the square root:
- \( \sqrt{72} = \sqrt{(2 × 2) × (3 × 3) × 2} \)
- \( \sqrt{72} = 2 × 3 × \sqrt{2} \)
- \( \sqrt{72} = 6 \sqrt{2} \)
Therefore, \( \sqrt{72} \) simplifies to \( 6 \sqrt{2} \).
Example 2: Simplifying \( \sqrt{98} \)
- Factor the Radicand:
Break down 98 into its prime factors:
- 98 = 2 × 7 × 7
- Group the Factors:
Group the factors into pairs:
- 98 = 2 × (7 × 7)
- Extract the Perfect Squares:
Extract the pair of 7's from under the square root:
- \( \sqrt{98} = \sqrt{2 × 7^2} \)
- \( \sqrt{98} = 7 \sqrt{2} \)
Therefore, \( \sqrt{98} \) simplifies to \( 7 \sqrt{2} \).
Example 3: Simplifying \( \sqrt{180} \)
- Factor the Radicand:
Break down 180 into its prime factors:
- 180 = 2 × 2 × 3 × 3 × 5
- Group the Factors:
Group the factors into pairs:
- 180 = (2 × 2) × (3 × 3) × 5
- Extract the Perfect Squares:
Extract the pairs of 2's and 3's from under the square root:
- \( \sqrt{180} = \sqrt{(2 × 2) × (3 × 3) × 5} \)
- \( \sqrt{180} = 2 × 3 × \sqrt{5} \)
- \( \sqrt{180} = 6 \sqrt{5} \)
Therefore, \( \sqrt{180} \) simplifies to \( 6 \sqrt{5} \).
These examples show the step-by-step process of simplifying square root expressions, demonstrating how to factorize the radicand, group factors, and extract perfect squares. Practicing with different expressions helps in mastering this technique.
Advanced Techniques for Complex Expressions
Simplifying complex square root expressions often involves advanced techniques, especially when dealing with higher-order roots, variables, and nested radicals. Here are some detailed steps and methods for handling these complex expressions:
Handling Higher-Order Roots
Higher-order roots, such as cube roots or fourth roots, require similar simplification techniques but with additional considerations:
- Factor the Radicand:
Break down the number inside the higher-order root into its prime factors.
- For example, \( \sqrt[3]{54} \): 54 = 2 × 3 × 3 × 3
- Group the Factors:
Group the factors based on the root’s order. For cube roots, group into triples:
- 54 = 2 × (3 × 3 × 3)
- Extract the Groups:
Extract each group of factors from the root:
- \( \sqrt[3]{54} = \sqrt[3]{2 \times 3^3} = 3 \sqrt[3]{2} \)
Therefore, \( \sqrt[3]{54} \) simplifies to \( 3 \sqrt[3]{2} \).
Variables in Radicals
When variables are involved, apply the same principles to the variable parts:
- Factor the Expression:
Include variables in the factorization process.
- For example, \( \sqrt{50x^4} \): 50x^4 = 2 × 5 × 5 × x² × x²
- Group the Factors:
Group the constant and variable factors:
- 50x^4 = (5 × 5) × 2 × (x² × x²)
- Extract the Perfect Squares:
Extract each group of factors:
- \( \sqrt{50x^4} = \sqrt{(5^2) \times 2 \times (x^2)^2} \)
- \( \sqrt{50x^4} = 5x^2 \sqrt{2} \)
Therefore, \( \sqrt{50x^4} \) simplifies to \( 5x^2 \sqrt{2} \).
Nesting Radicals
Nested radicals involve roots within roots and require a methodical approach:
- Simplify the Inner Radical:
First, simplify the innermost radical.
- For example, \( \sqrt{3 + \sqrt{8}} \): Start with \( \sqrt{8} = 2 \sqrt{2} \)
- Substitute and Simplify:
Substitute the simplified inner radical back into the expression and simplify further:
- \( \sqrt{3 + 2 \sqrt{2}} \)
- Look for Patterns or Use Algebraic Methods:
In some cases, recognizing patterns or using algebraic identities, such as completing the square, can help simplify nested radicals.
- For example, \( \sqrt{3 + 2 \sqrt{2}} \) can be simplified by recognizing it as \( \sqrt{(\sqrt{2} + 1)^2} = \sqrt{2} + 1 \)
Therefore, \( \sqrt{3 + \sqrt{8}} \) simplifies to \( \sqrt{2} + 1 \).
By mastering these advanced techniques, you can simplify even the most complex square root expressions, making them easier to work with in various mathematical contexts.
Common Mistakes to Avoid
When simplifying square root expressions, it's easy to make mistakes that can lead to incorrect results. Here are some common mistakes to avoid, along with tips on how to prevent them:
1. Not Fully Factoring the Radicand
One of the most common mistakes is not breaking down the radicand completely into its prime factors.
- Example:
For \( \sqrt{72} \), an incomplete factorization might look like \( \sqrt{36 \times 2} = 6 \sqrt{2} \). While this is correct, further simplification might reveal a different approach.
- Solution:
Ensure you break down the radicand fully: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
2. Incorrectly Grouping Factors
Another mistake is grouping the factors incorrectly, which leads to wrong simplification.
- Example:
For \( \sqrt{50} \), incorrect grouping might be \( \sqrt{25 \times 2} \), resulting in \( 5 \sqrt{2} \), but this ignores other possible factor groups.
- Solution:
Group factors correctly by identifying pairs or sets of factors that are perfect squares: \( 50 = 2 \times 5 \times 5 \).
3. Forgetting to Simplify Variables
When variables are included, forgetting to apply the same simplification rules can result in mistakes.
- Example:
For \( \sqrt{18x^2} \), not simplifying the variable part might leave the expression as \( 3 \sqrt{2x^2} \), which is incorrect.
- Solution:
Factor both the numerical and variable parts: \( 18x^2 = 2 \times 3 \times 3 \times x^2 \) and simplify to \( 3x \sqrt{2} \).
4. Neglecting to Simplify Fully
Stopping the simplification process too early can leave the expression not fully simplified.
- Example:
For \( \sqrt{128} \), simplifying partially to \( 8 \sqrt{2} \) and stopping there is not incorrect, but further simplification can be done.
- Solution:
Continue simplifying until no further factors can be extracted: \( 128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^7 \). This fully simplifies to \( 8 \sqrt{2} \).
5. Misapplying Square Root Properties
Misunderstanding the properties of square roots, such as the distributive property, can lead to mistakes.
- Example:
Incorrectly applying \( \sqrt{a + b} = \sqrt{a} + \sqrt{b} \) is a common mistake. For instance, \( \sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16} \).
- Solution:
Remember that \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \) and always simplify inside the radical first: \( \sqrt{25} = 5 \).
By being aware of these common mistakes and following the correct steps, you can simplify square root expressions accurately and efficiently.
Applications of Simplified Square Roots in Real Life
Simplified square root expressions are not just abstract mathematical concepts; they have numerous practical applications in various fields. Here are some key areas where simplified square roots are used in real life:
-
Geometry and Trigonometry:
Simplified square roots are fundamental in geometry, especially when calculating distances. For example, the Pythagorean theorem uses square roots to determine the length of the hypotenuse in a right triangle:
\[
c = \sqrt{a^2 + b^2}
\]Here, simplifying the square root expression helps in obtaining the exact length of the hypotenuse.
-
Physics:
In physics, square roots appear in formulas related to motion and waves. For instance, the period \(T\) of a simple pendulum is given by:
\[
T = 2\pi \sqrt{\frac{L}{g}}
\]where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity. Simplifying the expression can make calculations more manageable.
-
Engineering:
Engineers use square roots in various calculations, such as determining the natural frequency of a system in mechanical engineering:
\[
f_n = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]where \(k\) is the stiffness of the system and \(m\) is the mass. Simplifying the square root helps in precise and efficient engineering design.
-
Finance:
Square roots are used in finance to calculate standard deviation, which measures the amount of variation or dispersion in a set of values:
\[
\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2}
\]Simplifying this expression helps in assessing risk and making informed investment decisions.
-
Computer Graphics:
In computer graphics, square roots are used in algorithms that calculate distances and lighting. For instance, the distance between two points in 3D space is calculated as:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]Simplifying these calculations can enhance rendering efficiency and accuracy.
-
Astronomy:
Astronomers use square roots in formulas to calculate various distances and properties of celestial bodies. For example, the escape velocity \(v_e\) from a planet is given by:
\[
v_e = \sqrt{\frac{2GM}{R}}
\]where \(G\) is the gravitational constant, \(M\) is the mass of the planet, and \(R\) is its radius. Simplifying this expression helps in understanding the dynamics of planetary motion.
Understanding and simplifying square root expressions are crucial for solving real-world problems efficiently and accurately across various disciplines.

Frequently Asked Questions (FAQs)
-
What is a square root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 × 3 = 9.
-
How do you simplify square root expressions?
Simplifying square root expressions involves factoring the number under the square root into its prime factors and then taking pairs of prime factors out of the square root. For instance, √18 can be simplified to 3√2 because 18 = 2 × 3 × 3.
-
What are perfect squares?
Perfect squares are numbers that have integers as their square roots. Examples include 4, 9, 16, and 25, which are the squares of 2, 3, 4, and 5, respectively.
-
How do you add and subtract square roots?
To add or subtract square roots, the values under the square roots must be the same. For example, √2 + 3√2 equals 4√2. However, √2 + √3 cannot be simplified further because the radicands (2 and 3) are different.
-
How do you multiply and divide square roots?
To multiply square roots, multiply the values under the square roots together and then simplify if possible. For example, √2 × √8 equals √16, which simplifies to 4. To divide square roots, divide the values under the square roots. For instance, √8 / √2 equals √4, which simplifies to 2.
-
Can you have a square root in the denominator?
It is generally preferred to rationalize the denominator, meaning to eliminate the square root from the denominator. This is done by multiplying both the numerator and the denominator by the square root that is in the denominator. For example, 1 / √2 is rationalized by multiplying by √2 / √2 to get √2 / 2.
-
What are some common mistakes to avoid when simplifying square root expressions?
Common mistakes include:
- Forgetting to simplify the expression fully
- Incorrectly adding or subtracting square roots with different radicands
- Not rationalizing the denominator
- Ignoring the properties of square roots, such as √a × √b = √(a × b)
How do you handle square roots of negative numbers?
Square roots of negative numbers involve imaginary numbers. The square root of -1 is represented as i. For example, the square root of -4 is 2i because 2i × 2i = -4.
-
What is the principal square root?
The principal square root of a number is the non-negative root. For example, the principal square root of 9 is 3, not -3.
-
Where are simplified square roots used in real life?
Simplified square roots are used in various fields such as physics, engineering, and finance to solve equations, model real-world phenomena, and perform calculations involving areas and volumes.
Additional Resources and Tools
Here are some additional resources and tools to help you further understand and simplify square root expressions:
-
MathCracker Simplifying Radicals Calculator:
This online tool helps simplify radical expressions by applying basic rules and properties of square roots. It covers multiplication and division of square roots and provides a detailed step-by-step solution.
-
Calculator Soup Square Root Calculator:
This calculator not only computes the principal square root but also simplifies radical expressions. It also identifies perfect squares and provides complex solutions for negative inputs.
-
Khan Academy - Simplifying Square Root Expressions:
Khan Academy offers a comprehensive set of lessons, videos, and practice exercises on simplifying square roots. It covers fundamental concepts and advanced techniques, ideal for self-paced learning.
-
Wolfram Alpha:
Wolfram Alpha is a powerful computational tool that can simplify square root expressions and provide step-by-step solutions. It is particularly useful for complex and large expressions.
-
Symbolab Simplify Calculator:
Symbolab offers a simplify calculator that provides detailed solutions for simplifying square root expressions. It also offers explanations for each step, making it a great learning tool.
These resources provide various tools and explanations to help you master the simplification of square root expressions. Whether you are a student, educator, or math enthusiast, these tools will enhance your understanding and problem-solving skills.
Conclusion and Final Tips
Simplifying square root expressions can be straightforward with practice and the right tools. Here are some final tips to ensure success in both manual and calculator-based simplifications:
-
Understand the Basics:
Ensure you have a solid grasp of the properties of square roots and the different techniques for simplification. Remember that the square root of a product can be split into the product of square roots, but this is not true for sums.
Example: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) but \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \).
-
Practice Prime Factorization:
Breaking down numbers into their prime factors can make simplification easier. For instance, simplifying \( \sqrt{72} \) involves recognizing that \( 72 = 2^3 \cdot 3^2 \), which simplifies to \( 6\sqrt{2} \).
-
Use a Calculator:
Leverage online calculators for complex expressions. These tools can handle large numbers and variables efficiently, providing both exact and decimal approximations.
- Symbolab Square Root Calculator
- Mathway Square Root Calculator
- Calculator Soup Square Root Calculator
-
Check Your Work:
Always verify your results, especially when simplifying manually. Recalculate the simplified expression to ensure it equals the original under the square root.
-
Learn From Mistakes:
Review any errors and understand why they occurred. This will help reinforce correct methods and prevent future mistakes.
By mastering these techniques and utilizing the available resources, you'll find that simplifying square root expressions becomes an easier and more intuitive process. Keep practicing, and don't hesitate to use calculators and online tools for assistance. Happy simplifying!
READ MORE:
Video hướng dẫn cách sử dụng máy tính TI-30xs mv để đơn giản hóa căn bậc hai. Phù hợp cho các bài toán đại số và học sinh chuẩn bị thi.
Đại số với TI-30xs mv - Đơn giản hóa căn bậc hai