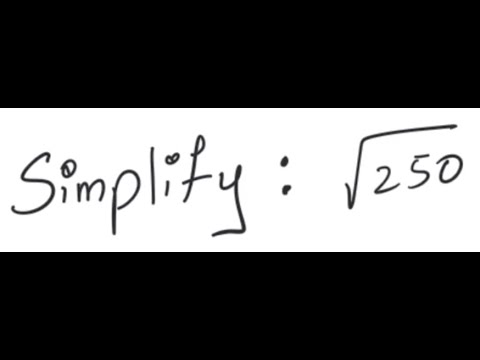Topic simplify the square root of 80: Understanding how to simplify the square root of 80 can be essential for students and math enthusiasts alike. This guide provides step-by-step methods to simplify √80 using prime factorization, repeated subtraction, and long division, making the process easy to grasp. Read on to enhance your mathematical skills and simplify square roots with confidence.
Table of Content
- Simplifying the Square Root of 80
- Introduction to Simplifying Square Roots
- Definition of Square Roots
- Step-by-Step Guide to Simplify the Square Root of 80
- Prime Factorization Method
- Perfect Squares and Radicals
- Example Problems and Solutions
- Using Calculators to Verify Results
- Related Mathematical Concepts
- FAQs on Square Roots
- Additional Resources and Practice Problems
- YOUTUBE: Hướng dẫn đơn giản hóa căn bậc hai của 80 (sqrt(80)) với các bước chi tiết và dễ hiểu.
Simplifying the Square Root of 80
The process of simplifying the square root of 80 involves several steps. Let's break it down:
Steps to Simplify \(\sqrt{80}\)
-
Rewrite 80 as a product of its prime factors:
\[
80 = 2 \times 2 \times 2 \times 2 \times 5 = 2^4 \times 5
\] -
Express the square root of 80 in terms of its prime factors:
\[
\sqrt{80} = \sqrt{2^4 \times 5}
\] -
Separate the factors under the square root:
\[
\sqrt{2^4 \times 5} = \sqrt{2^4} \times \sqrt{5}
\] -
Simplify the square root of 24:
\[
\sqrt{2^4} = 2^2 = 4
\] -
Combine the simplified factors:
\[
\sqrt{80} = 4 \sqrt{5}
\]
Thus, the simplified form of the square root of 80 is 4√5.
Decimal Form
The decimal approximation of the square root of 80 is:
\[
\sqrt{80} \approx 8.944
\]
Properties of the Square Root of 80
- The square root of 80 is an irrational number.
- It has both a positive and a negative value:
±8.944. - It is not a perfect square since no integer squared gives 80.
Examples and Applications
Consider a practical example:
Lucas wants to calculate the side length of his square land plot that has an area of 80 square feet. The side length of the land is \(\sqrt{80} = 4\sqrt{5}\) feet.
Conclusion
Simplifying square roots helps in understanding and solving various mathematical problems efficiently. The square root of 80 simplifies to 4√5, and its decimal form is approximately 8.944.
READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental concept in algebra that involves reducing a square root to its simplest form. This process makes it easier to work with the values in equations and other mathematical operations. To simplify the square root of 80, we break it down into its prime factors and identify any perfect squares.
Let's go through the steps to simplify the square root of 80:
- Identify the prime factors of 80. These are 2, 2, 2, 2, and 5.
- Group the factors into pairs of perfect squares. Here, we have \(2^2 \times 2^2 \times 5\).
- Rewrite the square root of 80 using these factors: \(\sqrt{80} = \sqrt{4 \times 4 \times 5}\).
- Take the square root of the perfect squares out of the radical: \(\sqrt{4} \times \sqrt{4} \times \sqrt{5} = 4\sqrt{5}\).
Thus, the simplified form of \(\sqrt{80}\) is \(4\sqrt{5}\). This method of simplification can be applied to any square root, allowing for easier calculation and comprehension.
Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For any non-negative number a, the square root of a is denoted as √a and is a number x such that x × x = a. Mathematically, it is represented as:
\[ x = \sqrt{a} \]
For example, the square root of 16 is 4, since 4 × 4 = 16. This can be expressed as:
\[ \sqrt{16} = 4 \]
In general, for any positive number a:
- If x × x = a, then x is the square root of a.
- The square root of a is denoted as √a.
- Every positive number has two square roots: a positive square root and a negative square root. For example, the square roots of 9 are 3 and -3, since both 3 × 3 and (-3) × (-3) equal 9.
Square roots are often used in various areas of mathematics, including algebra and geometry. They are essential for solving quadratic equations and for determining distances in coordinate systems. The square root function is a fundamental concept in mathematics and is widely applied in many scientific and engineering disciplines.
When simplifying square roots, the goal is to express the square root in its simplest radical form. This involves breaking down the number inside the square root into its prime factors and then simplifying using perfect squares.
To summarize, the square root of a number is a value that, when squared, equals the original number. Understanding square roots is crucial for simplifying radical expressions and solving various mathematical problems.
Step-by-Step Guide to Simplify the Square Root of 80
Simplifying the square root of 80 involves breaking it down into its simplest radical form. Follow these steps to simplify √80:
-
List the Factors: Identify all the factors of 80.
- 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
-
Find Perfect Squares: From the list of factors, identify the perfect squares.
- 1, 4, 16
-
Divide by the Largest Perfect Square: Divide 80 by the largest perfect square identified in the previous step.
- 80 ÷ 16 = 5
-
Calculate the Square Root of the Perfect Square: Find the square root of the largest perfect square.
- √16 = 4
-
Combine the Results: Multiply the square root of the perfect square by the square root of the remaining factor.
- √80 = 4√5
Therefore, the simplest form of √80 is 4√5.
In decimal form, this is approximately equal to 8.9443.
Prime Factorization Method
Prime factorization is a method used to simplify square roots by breaking down the number into its prime factors. Here is a step-by-step guide to simplify the square root of 80 using this method:
- Find the prime factors of 80:
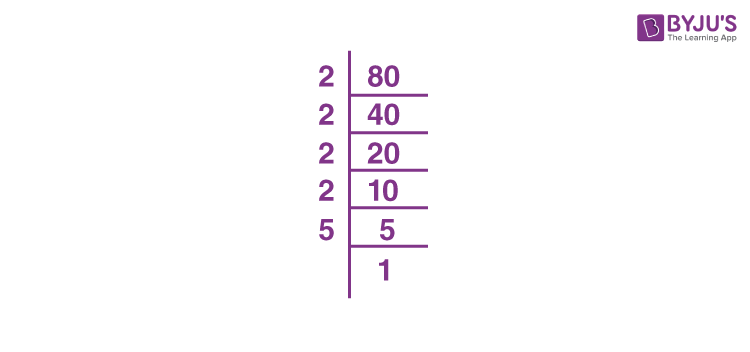
First, break down 80 into its prime factors:
\( 80 = 2 \times 40 \)
\( 40 = 2 \times 20 \)
\( 20 = 2 \times 10 \)
\( 10 = 2 \times 5 \)Therefore, \( 80 = 2 \times 2 \times 2 \times 2 \times 5 \) or \( 80 = 2^4 \times 5 \).
- Group the prime factors:
According to the properties of square roots, we can group the factors into pairs of two:
\( \sqrt{80} = \sqrt{2^4 \times 5} \)
Since \( 2^4 \) can be grouped as \( (2^2) \times (2^2) \):
\( \sqrt{80} = \sqrt{(2^2 \times 2^2) \times 5} \)
- Simplify the square root:
Extract the pairs from under the square root sign:
\( \sqrt{(2^2 \times 2^2) \times 5} = \sqrt{2^2} \times \sqrt{2^2} \times \sqrt{5} \)
Since \( \sqrt{2^2} = 2 \):
\( \sqrt{80} = 2 \times 2 \times \sqrt{5} \)
\( \sqrt{80} = 4\sqrt{5} \)
Thus, the simplified form of the square root of 80 is \( 4\sqrt{5} \).

Perfect Squares and Radicals
In order to simplify radicals, particularly square roots, it's essential to understand the role of perfect squares. A perfect square is a number that can be expressed as the product of an integer with itself. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be written as 12, 22, 32, 42, and 52, respectively.
When simplifying square roots, we aim to factor the number under the square root (radicand) into a product of perfect squares and other factors. This allows us to simplify the radical by taking the square root of the perfect square factor.
Steps to Simplify Radicals Using Perfect Squares
- Identify the largest perfect square factor of the radicand.
- Rewrite the radicand as a product of the perfect square and another factor.
- Use the property
$$\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}$$ to separate the square root into two parts. - Simplify the square root of the perfect square.
- Multiply any remaining square roots if necessary.
Example: Simplify \( \sqrt{80} \)
Let's simplify \( \sqrt{80} \) step by step:
- Find the largest perfect square factor of 80. The factors of 80 are 1, 4, 16, 20, etc. The largest perfect square factor is 16.
- Rewrite 80 as the product of 16 and 5:
$$80 = 16 \times 5$$ . - Apply the property of square roots:
$$\sqrt{80} = \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5}$$ . - Simplify \( \sqrt{16} \) to 4:
$$\sqrt{16} = 4$$ . - Combine the results:
$$\sqrt{80} = 4 \sqrt{5}$$ .
Thus, the simplified form of \( \sqrt{80} \) is \( 4 \sqrt{5} \).
Importance of Perfect Squares in Simplifying Radicals
Perfect squares are fundamental in simplifying radicals because they help reduce the radicand to its simplest form. This simplification is crucial in solving mathematical problems efficiently and accurately.
Additional Examples
- Simplify \( \sqrt{50} \):
- Largest perfect square factor of 50 is 25.
- Rewrite: \( 50 = 25 \times 2 \).
- Apply property: \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} \).
- Simplify: \( \sqrt{25} = 5 \).
- Result: \( \sqrt{50} = 5 \sqrt{2} \).
- Simplify \( \sqrt{45} \):
- Largest perfect square factor of 45 is 9.
- Rewrite: \( 45 = 9 \times 5 \).
- Apply property: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} \).
- Simplify: \( \sqrt{9} = 3 \).
- Result: \( \sqrt{45} = 3 \sqrt{5} \).
Example Problems and Solutions
Let's explore some example problems to understand how to simplify square roots, specifically focusing on the square root of 80. By working through these examples, you'll see the process and patterns involved in simplifying square roots.
Example 1: Simplify \(\sqrt{80}\)
- Prime factorize the number under the square root:
- 80 can be factorized into \(80 = 2 \times 40\)
- Continue factorizing: \(40 = 2 \times 20\)
- And further: \(20 = 2 \times 10\)
- Finally: \(10 = 2 \times 5\)
- So, \(80 = 2 \times 2 \times 2 \times 2 \times 5\) or \(80 = 2^4 \times 5\)
- Group the prime factors into pairs:
- \(80 = (2^2 \times 2^2 \times 5)\)
- Each pair of 2s can be taken out of the square root as a single 2
- Simplify the expression:
- \(\sqrt{80} = \sqrt{(2^2 \times 2^2 \times 5)}\)
- \(\sqrt{80} = 2 \times 2 \times \sqrt{5}\)
- \(\sqrt{80} = 4\sqrt{5}\)
So, \(\sqrt{80} = 4\sqrt{5}\).
Example 2: Simplify \(\sqrt{72}\)
- Prime factorize the number under the square root:
- 72 can be factorized into \(72 = 2 \times 36\)
- Continue factorizing: \(36 = 2 \times 18\)
- And further: \(18 = 2 \times 9\)
- Finally: \(9 = 3 \times 3\)
- So, \(72 = 2^3 \times 3^2\)
- Group the prime factors into pairs:
- \(72 = (2^2 \times 2 \times 3^2)\)
- Each pair of 2s and 3s can be taken out of the square root as single 2 and 3, respectively
- Simplify the expression:
- \(\sqrt{72} = \sqrt{(2^2 \times 3^2 \times 2)}\)
- \(\sqrt{72} = 2 \times 3 \times \sqrt{2}\)
- \(\sqrt{72} = 6\sqrt{2}\)
So, \(\sqrt{72} = 6\sqrt{2}\).
Example 3: Simplify \(\sqrt{50}\)
- Prime factorize the number under the square root:
- 50 can be factorized into \(50 = 2 \times 25\)
- And further: \(25 = 5 \times 5\)
- So, \(50 = 2 \times 5^2\)
- Group the prime factors into pairs:
- \(50 = (5^2 \times 2)\)
- Each pair of 5s can be taken out of the square root as a single 5
- Simplify the expression:
- \(\sqrt{50} = \sqrt{(5^2 \times 2)}\)
- \(\sqrt{50} = 5\sqrt{2}\)
So, \(\sqrt{50} = 5\sqrt{2}\).
Using Calculators to Verify Results
Using a calculator to verify the simplification of the square root of 80 can be very helpful. Here are the steps to do this:
-
Enter the expression into the calculator. For most calculators, you can directly input the number and press the square root (√) button. For example, enter
80and then press√. -
The calculator will display the decimal form of the square root of 80. The result should be approximately
8.94427191. -
To verify the simplified form, you need to understand the prime factorization method we used. The square root of 80 simplified is
4√5. -
Using the calculator, find the square root of 5 by entering
5and pressing√. The result is approximately2.236067977. -
Multiply this result by 4 (since the simplified form is
4√5). So,4 * 2.236067977 ≈ 8.94427191, which matches the initial decimal result.
Here is a quick reference table for clarity:
| Step | Action | Result |
|---|---|---|
| 1 | Enter 80 and press √ | 8.94427191 |
| 2 | Enter 5 and press √ | 2.236067977 |
| 3 | Multiply the result by 4 | 8.94427191 |
By following these steps, you can easily verify the simplification of the square root of 80 using any standard calculator.
Related Mathematical Concepts
Understanding the process of simplifying the square root of 80 involves several related mathematical concepts. These concepts provide a broader foundation for working with square roots and radicals in various mathematical contexts. Below are some of the key related concepts:
1. Properties of Square Roots
Square roots have specific properties that help in their simplification and manipulation:
- Product Property: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Even and Odd Exponents: For any real number \(a\), \(\sqrt{a^2} = |a|\)
2. Rationalizing the Denominator
When dealing with fractions involving square roots, it's often necessary to rationalize the denominator to simplify the expression:
- Example: \(\frac{1}{\sqrt{2}}\) can be rationalized to \(\frac{\sqrt{2}}{2}\)
- This process involves multiplying the numerator and the denominator by the conjugate of the denominator if it is a binomial radical expression.
3. Perfect Squares
Recognizing perfect squares is crucial in simplifying square roots. Perfect squares are numbers like 1, 4, 9, 16, 25, etc., where each can be expressed as the square of an integer:
- \(1 = 1^2\)
- \(4 = 2^2\)
- \(9 = 3^2\)
- And so on...
4. Prime Factorization
Prime factorization is the process of breaking down a number into its prime factors. This is particularly useful in simplifying square roots:
- Example: The prime factorization of 80 is \(2^4 \cdot 5\).
- By identifying pairs of prime factors, we can simplify the square root: \(\sqrt{80} = \sqrt{2^4 \cdot 5} = 2^2 \cdot \sqrt{5} = 4\sqrt{5}\).
5. Simplifying Radical Expressions
Simplifying radical expressions often involves combining like terms and using the properties of square roots:
- Example: Simplify \(\sqrt{50} + 2\sqrt{2}\):
- First, simplify each term if possible: \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
- Combine like terms: \(5\sqrt{2} + 2\sqrt{2} = 7\sqrt{2}\)
6. Approximating Square Roots
While exact values are ideal, sometimes we need approximate values for practical purposes. Estimation techniques include using nearby perfect squares and interpolation:
- Example: To approximate \(\sqrt{80}\), recognize it is between \(\sqrt{64} (8)\) and \(\sqrt{81} (9)\).
- Since 80 is closer to 81, \(\sqrt{80} \approx 8.9\).
7. Using Technology
Calculators and software tools can simplify and verify square root calculations:
- Most scientific calculators have a square root function, often denoted as \(\sqrt{}\).
- Software like WolframAlpha or graphing calculators can handle complex radical expressions.
These related concepts not only aid in simplifying specific problems like \(\sqrt{80}\) but also enhance overall mathematical problem-solving skills.
FAQs on Square Roots
Below are some frequently asked questions about square roots, along with their answers to help you understand and simplify square roots better.
-
Q: How do you simplify the square root of 80?
A: To simplify the square root of 80, you can use the prime factorization method:
- Find the prime factors of 80: \(80 = 2^4 \times 5\).
- Group the prime factors into pairs: \(2^4 = (2^2)^2\).
- Simplify the square root: \(\sqrt{80} = \sqrt{(2^2)^2 \times 5} = 2^2 \times \sqrt{5} = 4\sqrt{5}\).
So, \(\sqrt{80} = 4\sqrt{5}\).
-
Q: What is a perfect square?A: A perfect square is a number that can be expressed as the product of an integer with itself. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be written as \(1^2, 2^2, 3^2, 4^2,\) and \(5^2\) respectively.
-
Q: How do you simplify square roots that are not perfect squares?
A: To simplify square roots that are not perfect squares, find the largest perfect square factor of the number, factor it out, and simplify. For example, to simplify \(\sqrt{50}\):
- Find the largest perfect square factor of 50, which is 25.
- Rewrite the square root: \(\sqrt{50} = \sqrt{25 \times 2}\).
- Simplify: \(\sqrt{25} \times \sqrt{2} = 5\sqrt{2}\).
-
Q: Can you add or subtract square roots?A: You can add or subtract square roots only if the radicands (the numbers inside the square root) are the same. For example, \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\). However, \(\sqrt{2} + \sqrt{3}\) cannot be simplified further.
-
Q: How do you multiply and divide square roots?
A: To multiply square roots, multiply the radicands and take the square root of the product: \(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\). To divide square roots, divide the radicands and take the square root of the quotient: \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\).
Additional Resources and Practice Problems
To further enhance your understanding and skills in simplifying square roots, especially the square root of 80, here are some valuable resources and practice problems:
- Online Tutorials: There are several online platforms that offer step-by-step tutorials on simplifying square roots. These tutorials often include video explanations, interactive exercises, and quizzes to test your knowledge.
- - A comprehensive tutorial with practice exercises.
- - Additional practice problems and videos.
- Practice Worksheets: Printable worksheets can be a great way to practice simplifying square roots. They often include a variety of problems ranging from basic to advanced levels.
- - Offers a variety of worksheets on square roots and radicals.
- Interactive Calculators: Online calculators can help verify your solutions and understand the steps involved in simplifying square roots.
- - Provides a square root calculator with step-by-step solutions.
- Textbooks and Reference Books: Traditional textbooks often provide detailed explanations and numerous practice problems.
- "Algebra 1" by McGraw-Hill - A comprehensive algebra textbook that covers simplifying square roots in detail.
- Online Forums and Study Groups: Joining an online community or study group can be beneficial. You can ask questions, share problems, and get feedback from others.
- - A community for students and enthusiasts to discuss math problems and concepts.
These resources will help you practice and master the skill of simplifying square roots. Consistent practice and seeking help when needed are key to becoming proficient in this area of mathematics.
Hướng dẫn đơn giản hóa căn bậc hai của 80 (sqrt(80)) với các bước chi tiết và dễ hiểu.
Làm thế nào để Đơn giản hóa Căn bậc hai của 80: sqrt(80)
READ MORE:
Video hướng dẫn đơn giản hóa căn bậc hai của số 80 bằng cách sử dụng cây yếu tố. Học cách phân tích và tính toán nhanh chóng và dễ dàng.
Đơn Giản Hóa Căn Bậc Hai Bằng Cây Yếu Tố, sqrt(80)