Topic simplify square root 250: Unlock the secrets to simplifying the square root of 250 with our easy-to-follow guide. Whether you're a student or math enthusiast, this article provides clear, step-by-step instructions to simplify √250 effortlessly. Discover tips, tricks, and common pitfalls to avoid, ensuring you master this essential math skill with confidence.
Table of Content
- Simplify Square Root 250
- Introduction to Square Roots
- Understanding Square Roots
- Basics of Simplifying Square Roots
- Step-by-Step Guide to Simplifying √250
- Prime Factorization Method
- Breaking Down √250 into Factors
- Using Perfect Squares to Simplify
- Combining Like Terms
- Final Simplified Form of √250
- Common Mistakes to Avoid
- Additional Practice Problems
- Applications of Simplified Square Roots
- Conclusion and Summary
- YOUTUBE:
Simplify Square Root 250
The square root of 250 can be simplified as follows:
\[
\sqrt{250} = \sqrt{25 \times 10} = \sqrt{25} \times \sqrt{10} = 5\sqrt{10}
\]
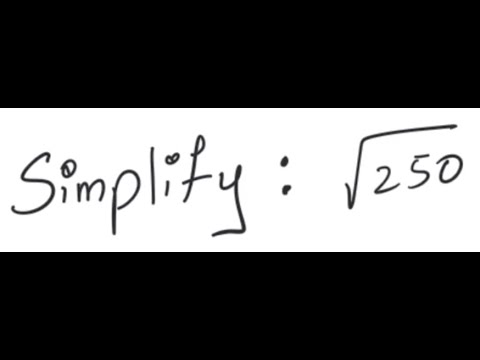
READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Understanding square roots is essential in various fields, from mathematics to engineering. This guide will help you grasp the concept of square roots and how to simplify them, using the square root of 250 as an example.
For example, the square root of 9 is 3, because \(3 \times 3 = 9\). Similarly, the square root of 16 is 4, because \(4 \times 4 = 16\).
To simplify square roots, especially non-perfect squares like 250, we follow a step-by-step approach:
- Prime Factorization: Break down the number into its prime factors.
- Identify Pairs: Group the prime factors into pairs.
- Simplify: Bring out one factor from each pair and multiply.
We will demonstrate these steps in detail to simplify \( \sqrt{250} \).
| Number | Prime Factors |
| 250 | 2, 5, 5, 5 |
Using this factorization, we can simplify \( \sqrt{250} \) as follows:
- \(250 = 2 \times 5^3\)
- Pairs of 5: \(5 \times 5\) forms a pair
- Take one 5 out of the square root: \(5 \sqrt{10}\)
Thus, \( \sqrt{250} \) simplifies to \( 5 \sqrt{10} \). This process will be detailed further in the following sections.
Understanding Square Roots
A square root of a number is a value that, when multiplied by itself, results in the original number. For example, the square root of 16 is 4 because \(4 \times 4 = 16\). The square root is denoted by the radical symbol \( \sqrt{} \).
There are a few key points to understand about square roots:
- Every positive number has two square roots: a positive and a negative one. For example, the square roots of 9 are 3 and -3, since \(3 \times 3 = 9\) and \((-3) \times (-3) = 9\).
- The principal square root is the non-negative root, which is usually what we refer to when we mention the square root of a number.
- Perfect squares are numbers whose square roots are integers. Examples include 1, 4, 9, 16, 25, and so on.
- Non-perfect squares result in irrational numbers when taking the square root. For instance, the square root of 2 is approximately 1.414, and it cannot be expressed as an exact fraction.
To simplify square roots, particularly those of non-perfect squares, we use methods such as prime factorization. This helps us break down the number under the radical into simpler components.
Let's take a closer look at simplifying the square root of 250.
- Prime Factorization: Decompose 250 into its prime factors.
- 250 = 2 × 125
- 125 = 5 × 25
- 25 = 5 × 5
- Therefore, 250 = 2 × 5 × 5 × 5
- Identify Pairs: Group the prime factors into pairs.
- Pairs of 5: \(5 \times 5\) forms a pair
- Simplify: Bring one factor from each pair outside the square root.
- Take one 5 out of the square root: \(5 \sqrt{10}\)
As a result, \( \sqrt{250} \) simplifies to \( 5 \sqrt{10} \). Understanding these principles is crucial for mastering the simplification of square roots.
Basics of Simplifying Square Roots
Simplifying square roots involves reducing a square root to its simplest form. This process is particularly useful for making complex calculations easier and more understandable. Let's explore the basic steps involved in simplifying square roots, using \( \sqrt{250} \) as an example.
Here are the fundamental steps:
- Prime Factorization: Break down the number under the square root into its prime factors.
- Identify Pairs: Group the prime factors into pairs of the same number.
- Simplify: Bring one factor from each pair outside the square root, multiplying them together. Any factors that don't pair up stay under the square root.
Let's apply these steps to \( \sqrt{250} \):
- Prime Factorization: Find the prime factors of 250.
- 250 can be divided by 2: \(250 \div 2 = 125\)
- 125 can be divided by 5: \(125 \div 5 = 25\)
- 25 is \(5 \times 5\)
- So, \(250 = 2 \times 5 \times 5 \times 5\)
- Identify Pairs: Group the prime factors into pairs.
- The pairs are: \(5 \times 5\)
- Remaining factors: \(2 \times 5\)
- Simplify: Bring one factor from each pair outside the square root.
- The pair of 5 comes out as a single 5: \(5\)
- The remaining factors under the square root: \(2 \times 5 = 10\)
- Thus, \( \sqrt{250} = 5 \sqrt{10}\)
In summary, the square root of 250 simplifies to \( 5 \sqrt{10} \). This method can be applied to simplify any square root, making complex expressions more manageable.
Step-by-Step Guide to Simplifying √250
Simplifying the square root of 250 involves a few straightforward steps. By breaking down the number into its prime factors and then simplifying, we can find a more manageable form. Follow these steps to simplify \( \sqrt{250} \):
- Prime Factorization: Decompose 250 into its prime factors.
- 250 is even, so divide by 2: \(250 \div 2 = 125\)
- 125 is divisible by 5: \(125 \div 5 = 25\)
- 25 is \(5 \times 5\)
- So, the prime factors of 250 are \(2 \times 5 \times 5 \times 5\)
- Identify Pairs: Group the prime factors into pairs of the same number.
- Pair of 5s: \(5 \times 5\)
- Remaining factors: \(2 \times 5\)
- Simplify: Bring one factor from each pair outside the square root.
- The pair of 5s comes out as a single 5: \(5\)
- Under the square root, we have \(2 \times 5 = 10\)
Thus, the simplified form of \( \sqrt{250} \) is:
\( \sqrt{250} = 5 \sqrt{10} \)
Let's review these steps in a concise table:
| Step | Description | Result |
|---|---|---|
| 1 | Prime Factorization | \(250 = 2 \times 5 \times 5 \times 5\) |
| 2 | Identify Pairs | Pairs: \(5 \times 5\), Remaining: \(2 \times 5\) |
| 3 | Simplify | \(5 \sqrt{10}\) |
By following these steps, you can simplify any square root efficiently. For \( \sqrt{250} \), the result is \( 5 \sqrt{10} \), which is a much simpler form to work with in further calculations.

Prime Factorization Method
The prime factorization method is a powerful technique for simplifying square roots. By breaking down a number into its prime factors, we can easily identify pairs and simplify the square root. Here’s how to apply the prime factorization method to simplify \( \sqrt{250} \).
- Identify the Prime Factors:
- Start with the number 250.
- Since 250 is even, divide by 2: \(250 \div 2 = 125\).
- Next, divide 125 by 5 (the smallest prime factor of 125): \(125 \div 5 = 25\).
- Finally, recognize that 25 is \(5 \times 5\).
- So, the prime factorization of 250 is \(2 \times 5 \times 5 \times 5\).
- Group the Prime Factors into Pairs:
- Pairs of 5s: \(5 \times 5\).
- Remaining factors: \(2 \times 5\).
- Simplify by Bringing One Factor from Each Pair Outside the Square Root:
- The pair of 5s becomes a single 5 outside the square root: \(5\).
- The remaining factors under the square root are \(2 \times 5 = 10\).
Thus, the simplified form of \( \sqrt{250} \) is:
\( \sqrt{250} = 5 \sqrt{10} \)
Here’s a summary in a table format:
| Step | Description | Result |
|---|---|---|
| 1 | Identify the Prime Factors | \(250 = 2 \times 5 \times 5 \times 5\) |
| 2 | Group the Prime Factors | Pairs: \(5 \times 5\), Remaining: \(2 \times 5\) |
| 3 | Simplify | \(5 \sqrt{10}\) |
Using the prime factorization method, we have successfully simplified \( \sqrt{250} \) to \( 5 \sqrt{10} \). This method is useful for simplifying square roots of any non-perfect square.
Breaking Down √250 into Factors
To simplify the square root of 250, we first need to break it down into its prime factors. This process involves dividing the number into smaller components that are prime numbers. Here's a detailed, step-by-step method for breaking down \( \sqrt{250} \) into factors:
- Find the Smallest Prime Factor:
- Start with the number 250.
- Since 250 is even, divide by 2 (the smallest prime number): \(250 \div 2 = 125\).
- Continue with the Next Prime Factors:
- Next, take 125 and find the smallest prime factor. It’s divisible by 5: \(125 \div 5 = 25\).
- Then, take 25 and find the smallest prime factor. Again, it’s divisible by 5: \(25 \div 5 = 5\).
- Finally, recognize that 5 is a prime number.
- Express 250 as a Product of Its Prime Factors:
- Now, write 250 as a product of these prime factors: \(250 = 2 \times 5 \times 5 \times 5\).
We can summarize the factorization of 250 in the following table:
| Step | Operation | Result |
|---|---|---|
| 1 | 250 divided by 2 | 125 |
| 2 | 125 divided by 5 | 25 |
| 3 | 25 divided by 5 | 5 |
| 4 | 5 is a prime number | 5 |
Thus, the prime factorization of 250 is \(2 \times 5 \times 5 \times 5\).
By breaking down \( \sqrt{250} \) into these factors, we can easily identify pairs of prime factors, which will help us simplify the square root further in the next steps.
Using Perfect Squares to Simplify
One effective method for simplifying square roots is using perfect squares. Perfect squares are numbers whose square roots are integers, such as 4, 9, 16, 25, and so on. By recognizing and using these perfect squares, we can simplify more complex square roots like \( \sqrt{250} \). Here’s a step-by-step guide:
- Identify Perfect Square Factors:
- First, identify any perfect square factors of 250. In this case, 25 is a perfect square factor since \( 25 = 5 \times 5 \) and \( \sqrt{25} = 5 \).
- Rewrite the Square Root:
- Express 250 as a product of its perfect square factor and another number: \( 250 = 25 \times 10 \).
- Separate the Square Root:
- Use the property of square roots that states \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{250} = \sqrt{25 \times 10} = \sqrt{25} \times \sqrt{10} \).
- Simplify:
- Simplify the perfect square: \( \sqrt{25} = 5 \).
- Combine the results: \( \sqrt{250} = 5 \times \sqrt{10} \).
Thus, by using perfect squares, we have simplified \( \sqrt{250} \) to \( 5 \sqrt{10} \).
Here's a summary in a table format:
| Step | Operation | Result |
|---|---|---|
| 1 | Identify perfect square factors | 25 is a perfect square factor of 250 |
| 2 | Rewrite the square root | \(250 = 25 \times 10\) |
| 3 | Separate the square root | \(\sqrt{250} = \sqrt{25} \times \sqrt{10}\) |
| 4 | Simplify | \(5 \sqrt{10}\) |
By following these steps and using perfect squares, you can simplify square roots more effectively, making complex calculations easier to handle.
Combining Like Terms
Combining like terms is a crucial step in simplifying expressions involving square roots. Like terms are terms that contain the same variable raised to the same power. When simplifying square roots, we focus on combining square roots that have the same radicand (the number inside the square root). Here’s how to combine like terms in the context of simplifying \( \sqrt{250} \):
- Break Down the Expression:
- We already know that \( \sqrt{250} = 5 \sqrt{10} \).
- Consider if there are other terms involving \( \sqrt{10} \) in the expression.
- Identify Like Terms:
- Like terms will have the same square root component, such as \( \sqrt{10} \).
- For example, if the expression is \( 5 \sqrt{10} + 3 \sqrt{10} \), both terms are like terms because they contain \( \sqrt{10} \).
- Combine the Coefficients:
- Add or subtract the coefficients of the like terms.
- For \( 5 \sqrt{10} + 3 \sqrt{10} \), combine the coefficients: \( 5 + 3 = 8 \).
- The result is \( 8 \sqrt{10} \).
- Simplify the Expression:
- After combining the like terms, ensure the expression is in its simplest form.
Let’s summarize this process in a table:
| Step | Operation | Result |
|---|---|---|
| 1 | Break Down the Expression | \( \sqrt{250} = 5 \sqrt{10} \) |
| 2 | Identify Like Terms | \( 5 \sqrt{10} \) and \( 3 \sqrt{10} \) are like terms |
| 3 | Combine the Coefficients | \( 5 + 3 = 8 \) |
| 4 | Simplify the Expression | \( 8 \sqrt{10} \) |
In conclusion, combining like terms allows us to simplify expressions efficiently. For instance, \( 5 \sqrt{10} + 3 \sqrt{10} \) simplifies to \( 8 \sqrt{10} \). This process is invaluable in making complex expressions more manageable.
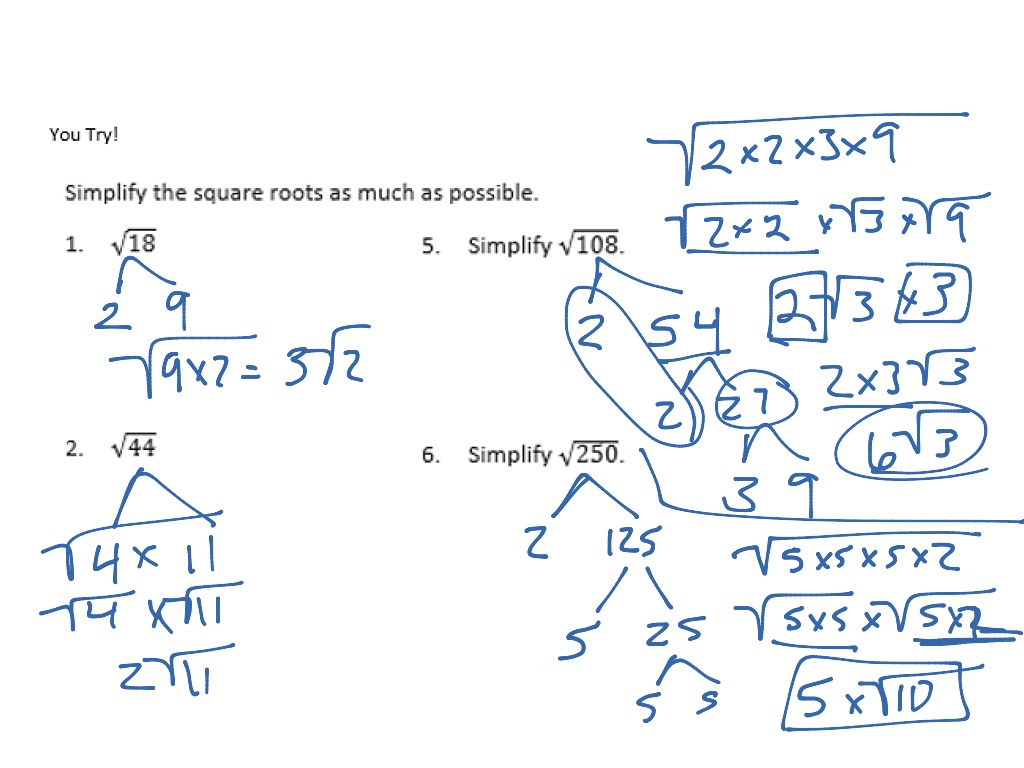
Final Simplified Form of √250
To simplify the square root of 250, we follow these steps:
-
Prime Factorization: Break down 250 into its prime factors.
250 = 2 × 5 × 5 × 5
-
Group the Factors: Group the prime factors into pairs of the same number.
250 = (5 × 5) × (2 × 5)
-
Simplify the Square Root: Take the square root of each pair of identical factors. For any pair, one factor comes out of the square root.
√250 = √(52 × 10) = 5√10
-
Final Simplified Form: The simplified form of the square root of 250 is:
√250 = 5√10
In decimal form, the square root of 250 is approximately:
√250 ≈ 15.81139
Therefore, the final simplified form of √250 is 5√10.
Common Mistakes to Avoid
When simplifying the square root of 250, it's important to be aware of some common mistakes that can lead to incorrect results. Here are a few to watch out for:
- Incorrect Prime Factorization: Ensure you correctly identify the prime factors of 250. The prime factorization should be \(250 = 2 \times 5^3\), but a common mistake is to miscalculate or miss a factor.
- Misapplying Square Root Rules: Remember the property \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\). Misapplying this rule can lead to errors. For example, incorrectly splitting \( \sqrt{250} \) as \( \sqrt{25 \times 10} = 5 \times \sqrt{10}\) instead of \( \sqrt{250} = 5\sqrt{10} \).
- Skipping Steps in Simplification: It's crucial to follow all steps in the simplification process. First, identify the largest perfect square factor of 250, which is 25. Then, simplify it correctly: \( \sqrt{250} = \sqrt{25 \times 10} = 5\sqrt{10} \).
- Misinterpreting Decimal Approximations: The decimal approximation of \(\sqrt{250}\) is approximately 15.81. Be cautious not to confuse this approximation with the exact simplified form \(5\sqrt{10}\).
- Forgetting to Simplify Completely: Sometimes, after finding the prime factors, it's easy to forget to simplify completely. Always check if the remaining expression under the radical can be simplified further.
- Using Incorrect Values: Double-check calculations and ensure correct multiplication and division when breaking down the square root.
By avoiding these common mistakes, you can ensure your simplification of \(\sqrt{250}\) is accurate and straightforward.
Additional Practice Problems
Practicing additional problems can help reinforce your understanding of simplifying square roots. Here are some practice problems to work through, complete with solutions to check your work.
- Simplify \( \sqrt{72} \)
- Prime factorize 72: \( 72 = 2^3 \times 3^2 \)
- Take out pairs of prime factors: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = 2 \times 3 \times \sqrt{2} \)
- Final simplified form: \( \sqrt{72} = 6\sqrt{2} \)
- Simplify \( \sqrt{98} \)
- Prime factorize 98: \( 98 = 2 \times 7^2 \)
- Take out pairs of prime factors: \( \sqrt{98} = \sqrt{2 \times 7^2} = 7 \times \sqrt{2} \)
- Final simplified form: \( \sqrt{98} = 7\sqrt{2} \)
- Simplify \( \sqrt{200} \)
- Prime factorize 200: \( 200 = 2^3 \times 5^2 \)
- Take out pairs of prime factors: \( \sqrt{200} = \sqrt{2^3 \times 5^2} = 5 \times 2 \times \sqrt{2} \)
- Final simplified form: \( \sqrt{200} = 10\sqrt{2} \)
- Simplify \( \sqrt{245} \)
- Prime factorize 245: \( 245 = 5 \times 7^2 \)
- Take out pairs of prime factors: \( \sqrt{245} = \sqrt{5 \times 7^2} = 7 \times \sqrt{5} \)
- Final simplified form: \( \sqrt{245} = 7\sqrt{5} \)
- Simplify \( \sqrt{360} \)
- Prime factorize 360: \( 360 = 2^3 \times 3^2 \times 5 \)
- Take out pairs of prime factors: \( \sqrt{360} = \sqrt{2^3 \times 3^2 \times 5} = 3 \times 2 \times \sqrt{10} \)
- Final simplified form: \( \sqrt{360} = 6\sqrt{10} \)
Working through these problems will give you a solid foundation in simplifying square roots. Make sure to practice with different numbers to become more confident in the process.
Applications of Simplified Square Roots
Simplified square roots, such as \( \sqrt{250} = 5\sqrt{10} \), have a wide range of practical applications in various fields. Understanding these applications helps illustrate the importance and utility of mathematical concepts in everyday life and professional fields.
1. Architecture and Engineering
In architecture and engineering, square roots are essential for calculating distances and materials needed for construction projects. For example, when designing circular or curved structures, architects often use square roots to determine areas and volumes accurately. The simplified form of square roots makes these calculations more manageable and precise.
2. Finance
In finance, square roots are used to calculate the standard deviation, a measure of volatility or risk in investment portfolios. By simplifying square roots, financial analysts can more easily interpret and compare the volatility of different investments, aiding in better decision-making.
3. Physics and Science
Many formulas in physics involve square roots, especially those related to force, energy, and motion. For example, the formula for kinetic energy \( E_k = \frac{1}{2}mv^2 \) can be rearranged to solve for velocity, requiring the use of square roots. Simplifying these square roots helps physicists and engineers solve problems more efficiently.
4. Navigation and Geography
In navigation and geography, the Pythagorean theorem, which involves square roots, is used to calculate the shortest distance between two points on a map. For instance, if the distance between two points forms a right triangle, the hypotenuse (the shortest path) can be found using square roots. Simplifying these calculations aids in more accurate and faster route planning.
5. Computer Graphics
Square roots are used in computer graphics to normalize vectors, which is crucial for rendering scenes accurately. Normalizing a vector involves dividing the vector by its length, which requires calculating the square root of the sum of the squares of its components. Simplified square roots streamline this process, improving the efficiency and quality of graphical computations.
By understanding and applying simplified square roots in these fields, professionals can achieve more accurate results and optimize their workflows, demonstrating the practical value of mathematical simplification.

Conclusion and Summary
In this guide, we have thoroughly explored the process of simplifying the square root of 250. By understanding and applying the steps involved, we were able to express √250 in its simplest radical form. Let's summarize the key points covered:
- The prime factorization method was used to break down 250 into its prime factors: \(250 = 2 \times 5^2 \times 5\).
- We identified the largest perfect square factor, which is 25, to simplify the square root.
- Using the property of square roots, we rewrote √250 as \( \sqrt{25 \times 10} \) and further simplified it to \( 5\sqrt{10} \).
The final simplified form of the square root of 250 is:
\[\sqrt{250} = 5\sqrt{10}\]
This simplification process helps in various applications, such as solving mathematical problems and real-life scenarios involving measurements and calculations. Understanding how to simplify square roots enhances your problem-solving skills and mathematical fluency.
We hope this comprehensive guide has provided you with a clear understanding of how to simplify square roots, particularly for the example of √250. Practice with additional problems and explore more complex scenarios to further strengthen your grasp of this concept.
Radicals: Đơn giản hóa √(250)
READ MORE:
Radicals: Đơn giản hóa 5 / [3]√(250)











