6 Square Root of 5: Understanding and Applying This Expression

The mathematical expression 6 \sqrt{5} combines a constant multiplier with the square root of a number. Here, the constant is 6, and the number under the square root is 5.

Mathematical Representation

The expression 6 \sqrt{5} can be expanded as follows:

$$ 6 \sqrt{5} = 6 \times \sqrt{5} $$

Decimal Approximation

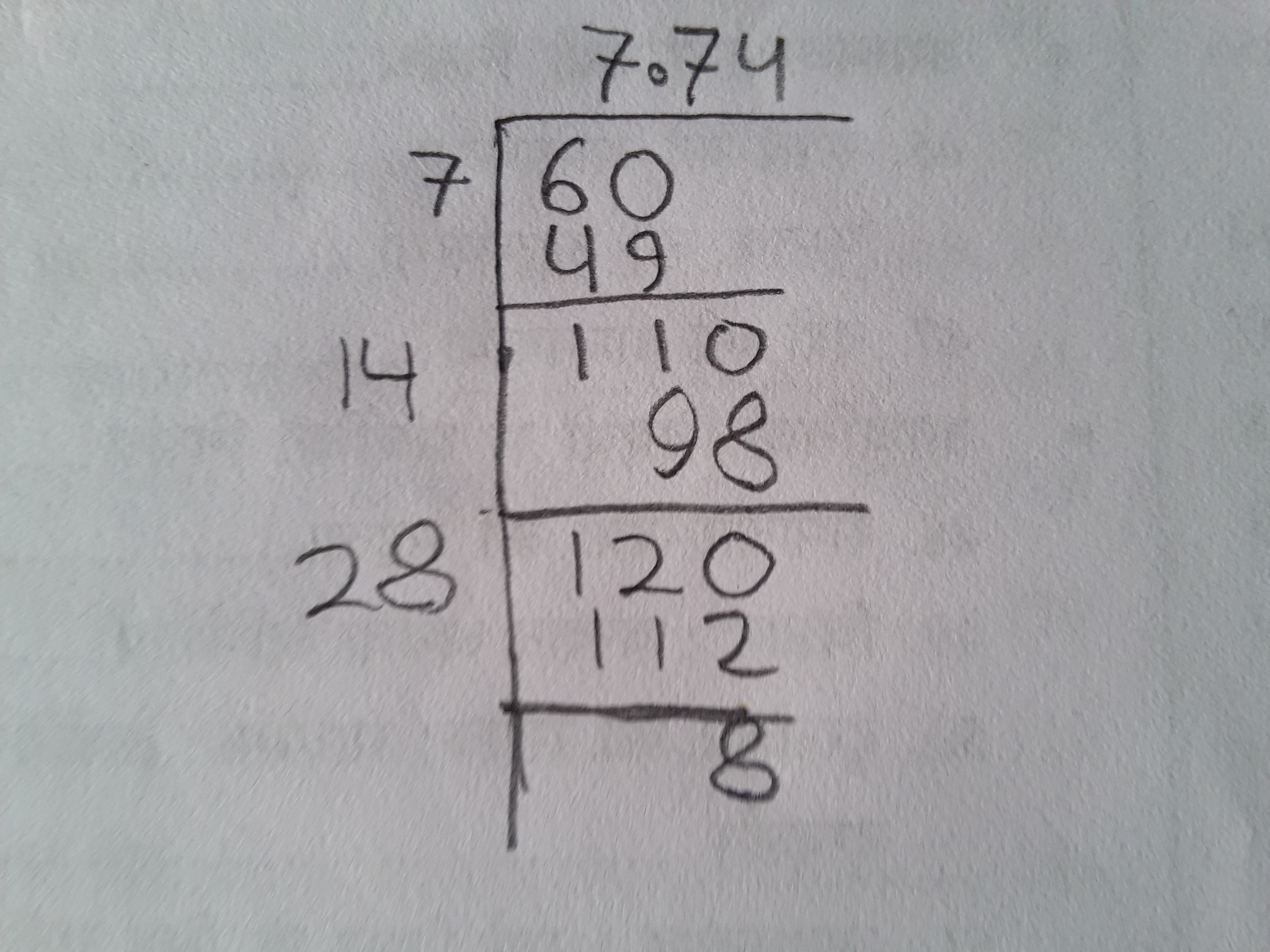
The square root of 5 is approximately 2.236. Therefore, the expression can be approximated as:

$$ 6 \sqrt{5} \approx 6 \times 2.236 = 13.416 $$

Properties

• Irrational Number: The square root of 5 is an irrational number, meaning it cannot be expressed as a simple fraction.
• Multiplication: Multiplying 6 by the square root of 5 scales the square root proportionally.

Usage in Mathematics

The expression 6 \sqrt{5} appears in various mathematical contexts, including:

1. Geometry: Involving diagonal lengths in certain polygons.
2. Trigonometry: Involving sine and cosine functions where radical expressions arise.
3. Physics: In formulas for wave functions and other scenarios where square roots of non-square numbers are involved.

Visualization

To visualize 6 \sqrt{5}, imagine the geometric interpretation of \sqrt{5} as a length and multiplying it by 6 scales the length by this factor:

$$ \text{If } \sqrt{5} \text{ represents a length, then } 6 \sqrt{5} \text{ represents six times that length.} $$

Conclusion

The expression 6 \sqrt{5} combines a whole number with a square root, leading to a number that is both useful in theoretical mathematics and practical applications.

The expression 6 \sqrt{5} represents the product of the integer 6 and the square root of 5, a fundamental irrational number. This combination is useful in various mathematical and scientific contexts.

To understand 6 \sqrt{5}, consider the following:

1. Definition: The square root of 5, denoted as \sqrt{5}, is a number which, when multiplied by itself, gives 5. Hence, \sqrt{5} \approx 2.236.
2. Multiplication: Multiplying 6 by \sqrt{5} yields 6 \sqrt{5}, combining the scaling factor of 6 with the irrational value of \sqrt{5}. Mathematically, this is written as:

   
   $$ 6 \sqrt{5} = 6 \times \sqrt{5} \approx 6 \times 2.236 = 13.416 $$

3. Properties:
   • Irrationality: \sqrt{5} is irrational, meaning it cannot be precisely expressed as a fraction.
   • Scaling: The factor 6 scales \sqrt{5}, effectively enlarging its value by 6 times.
4. Visualization: If you imagine \sqrt{5} as a length on a number line, then 6 \sqrt{5} represents this length repeated 6 times.

This introduction sets the stage for a deeper exploration of 6 \sqrt{5} in mathematical, geometric, and applied contexts, demonstrating its significance and utility.

The expression 6 \sqrt{5} combines a rational number (6) and an irrational number (the square root of 5), resulting in a unique product.

Here's a detailed step-by-step breakdown:

1. Square Root of 5:

   The square root of 5, denoted as \sqrt{5}, is the number which, when multiplied by itself, equals 5:

   
   $$ \sqrt{5} \times \sqrt{5} = 5 $$

2. Approximate Value:

   The square root of 5 is approximately equal to 2.236:

   
   $$ \sqrt{5} \approx 2.236 $$

3. Multiplication:

   When the integer 6 is multiplied by the square root of 5, the expression becomes:

   
   $$ 6 \sqrt{5} = 6 \times \sqrt{5} $$

   Substituting the approximate value:

   
   $$ 6 \times 2.236 = 13.416 $$

4. Properties:
   • Rational and Irrational Components: Combining a rational number (6) with an irrational number (\sqrt{5}) results in an irrational product.
   • Non-Simplification: The expression 6 \sqrt{5} cannot be simplified into a rational number.
   • Scaling Effect: The factor 6 scales the value of \sqrt{5}, increasing it proportionally.

In essence, 6 \sqrt{5} is a product that involves the multiplication of a whole number and an irrational square root, leading to an expression with unique mathematical properties and applications.

Calculating the decimal approximation of 6 \sqrt{5} involves understanding both the value of the square root of 5 and the multiplication process.

1. Find the Square Root of 5:

   The square root of 5 is an irrational number, approximately:

   
   $$ \sqrt{5} \approx 2.236067977 $$

2. Multiply by 6:

   To find 6 \sqrt{5}, multiply the square root of 5 by 6:

   
   $$ 6 \times \sqrt{5} = 6 \times 2.236067977 $$

3. Perform the Multiplication:

   Carrying out the multiplication gives:

   
   $$ 6 \times 2.236067977 \approx 13.41640786 $$

   For practical purposes, this is often rounded to:

   
   $$ \approx 13.416 $$

4. Table of Approximations:

   The following table illustrates various approximations for 6 \sqrt{5} at different decimal places:

   Decimal Places	Approximation
   2	13.42
   4	13.4164
   6	13.416408
   8	13.41640786

5. Practical Usage:
   • Rounded Values: For most applications, rounding to 2 or 4 decimal places is sufficient.
   • Precision Requirements: In scientific calculations, more precision may be required.

The decimal approximation of 6 \sqrt{5} is essential for practical applications where exact values of irrational numbers are impractical, allowing for effective and efficient computations.

The expression 6 \sqrt{5} has several distinct properties and characteristics that arise from its combination of a rational and an irrational number.

1. Irrational Nature:

   The square root of 5 (\sqrt{5}) is an irrational number, meaning it cannot be expressed exactly as a fraction. Thus, 6 \sqrt{5} also retains this irrational property.

2. Multiplicative Scaling:

   The integer 6 acts as a scaling factor. When multiplied by \sqrt{5}, it scales the square root, resulting in a larger irrational number:

   
   $$ 6 \times \sqrt{5} = 6 \sqrt{5} $$

3. Approximation:

   While 6 \sqrt{5} is irrational, it can be approximated to several decimal places for practical use:

   
   $$ 6 \sqrt{5} \approx 13.416 $$

4. Non-Reducibility:

   The expression 6 \sqrt{5} cannot be simplified into a fraction or another simpler form because of the irrational component \sqrt{5}.

5. Geometric Interpretation:

   Geometrically, if \sqrt{5} represents a length, then 6 \sqrt{5} represents a line segment six times longer than \sqrt{5}.

6. Applications:

   6 \sqrt{5} appears in various mathematical contexts, such as geometry, where lengths or distances are involved, and in physics, where irrational numbers can represent measurements and constants.

   • Geometry: Used in calculations involving diagonals of certain polygons.
   • Physics: Appears in wave functions and other equations where irrational numbers provide precise measurements.

These properties highlight the versatility and importance of the expression 6 \sqrt{5} in mathematical and applied fields, demonstrating its unique combination of rational and irrational elements.

The expression 6 \sqrt{5} can be understood geometrically by considering how square roots and scaling factors interact in geometric contexts.

1. Basic Concept of \sqrt{5}:

   The square root of 5 (\sqrt{5}) represents the length of the hypotenuse of a right triangle with sides of lengths 1 and 2, as shown by the Pythagorean theorem:

   
   $$ 1^2 + 2^2 = 5 \implies \sqrt{5} $$

   This length is approximately 2.236.

2. Scaling by 6:

   When the length \sqrt{5} is multiplied by 6, the result is a new length, 6 \sqrt{5}, which is six times the original hypotenuse. This can be visualized as extending the original hypotenuse length sixfold:

   
   $$ 6 \times \sqrt{5} $$

3. Geometric Representation:

   If \sqrt{5} represents a distance or a line segment, then 6 \sqrt{5} represents a line segment six times as long. This is useful in various geometric constructions, such as determining scaled distances or lengths in figures.

   Example:

   • Consider a line segment AB with length \sqrt{5}. If this segment is extended by a factor of 6, the new length AB' will be 6 \sqrt{5}.
4. Applications in Geometry:

   Understanding 6 \sqrt{5} is valuable in problems involving area, volume, and distances where irrational lengths need to be scaled:

   • Polygons: Calculating the lengths of diagonals in certain polygons, where scaling factors apply.
   • Circles: Determining the lengths of radii or chord distances that involve irrational numbers.
5. Visualization:

   To visualize 6 \sqrt{5}, imagine a number line where \sqrt{5} is represented. Multiplying this by 6 would mark a point six times further along the line, representing the new length:

   
   $$ \text{Number Line: } 0 \rightarrow \sqrt{5} \rightarrow 2\sqrt{5} \rightarrow ... \rightarrow 6\sqrt{5} $$

The geometric interpretation of 6 \sqrt{5} highlights its role in scaling distances and constructing figures in mathematical and practical applications, demonstrating its importance in visualizing and solving geometric problems.

The expression 6 \sqrt{5} is applied in various mathematical contexts, providing solutions and insights into different types of problems. Here are some key applications:

1. Geometry:
   • Diagonals of Polygons: In polygons such as pentagons, the length of diagonals can often be expressed using square roots. For instance, in a regular pentagon, the diagonal length can be related to \sqrt{5}. Scaling this length by 6 gives a practical method for calculating scaled geometric properties.
   • Right Triangles: In problems involving right triangles where the sides involve irrational lengths, multiplying by a factor such as 6 allows the calculation of scaled distances, such as:

     
     $$ \text{If } \text{hypotenuse} = \sqrt{5}, \text{ then scaled hypotenuse} = 6 \sqrt{5} $$

2. Trigonometry:

   In trigonometry, the expression 6 \sqrt{5} can be used in solving problems involving lengths of sides in triangles where one or more angles are known. It is particularly useful in scaling trigonometric functions or distances:

   
   $$ \text{If } \cos(\theta) = \frac{a}{6 \sqrt{5}}, \text{ then } a = 6 \sqrt{5} \cos(\theta) $$

3. Algebra:
   • Radical Equations: When solving equations involving radicals, expressions like 6 \sqrt{5} can be used to simplify or manipulate terms. For example, multiplying both sides of an equation by \sqrt{5} to eliminate the radical term.
   • Inequalities: In inequalities involving square roots, multiplying by constants like 6 helps in scaling and comparing values:

     
     $$ \text{If } x < \sqrt{5}, \text{ then } 6x < 6 \sqrt{5} $$

4. Calculus:
   • Integration: In integrals involving square roots, expressions like 6 \sqrt{5} help in scaling the function, making it easier to integrate. For instance:

     
     $$ \int_0^{1} 6 \sqrt{5} x^2 \, dx = 6 \sqrt{5} \left[ \frac{x^3}{3} \right]_0^1 = 2 \sqrt{5} $$

   • Derivatives: When taking derivatives of functions involving 6 \sqrt{5}, the constant can be factored out, simplifying the differentiation process:

     
     $$ \frac{d}{dx} [6 \sqrt{5} \cdot f(x)] = 6 \sqrt{5} \cdot f'(x) $$

5. Number Theory:

   In number theory, expressions involving 6 \sqrt{5} appear in problems dealing with irrational numbers, their properties, and their role in sequences or patterns. They help in exploring the relationship between integers and irrational values.

Overall, 6 \sqrt{5} is a versatile expression that finds applications in diverse mathematical areas, aiding in solving complex problems and providing a deeper understanding of mathematical relationships.

The expression 6 \sqrt{5} is used in various contexts within physics and engineering due to its role in representing scaled quantities and its appearance in formulas involving irrational numbers.

1. Wave Mechanics:

   In wave mechanics, expressions like 6 \sqrt{5} can represent amplitudes, frequencies, or other quantities when scaling wave functions. For instance:

   
   $$ \text{Wave function: } \psi(x, t) = A \sin(kx - \omega t) $$

   If A = 6 \sqrt{5}, it scales the amplitude of the wave, affecting its intensity or energy.

2. Resonance and Harmonics:

   In systems involving resonance, such as in mechanical or electrical engineering, 6 \sqrt{5} may describe a scaled natural frequency or harmonic. For example:

   
   $$ \text{Natural frequency: } \omega_n = 6 \sqrt{5} \text{ rad/s} $$

3. Structural Engineering:

   In structural engineering, 6 \sqrt{5} can appear in calculations involving forces, stresses, or dimensions when scaling properties of materials or structures. For example:

   • Stress Calculation: If a material’s stress is proportional to \sqrt{5}, scaling by 6 gives the effective stress:

     
     $$ \sigma = 6 \sqrt{5} \times \text{factor} $$

   • Length Scaling: When lengths or dimensions involve square roots, multiplying by 6 adjusts these to practical scales:

     
     $$ \text{Scaled length} = 6 \sqrt{5} \times \text{original length} $$

4. Electromagnetic Theory:

   In electromagnetic theory, 6 \sqrt{5} can be used in calculations involving fields, potentials, or forces, particularly when working with scaled quantities. For instance:

   
   $$ \text{Electric field strength: } E = 6 \sqrt{5} \frac{q}{r^2} $$

   This scaling helps in adjusting the magnitude of fields or forces in practical applications.

5. Acoustics:

   In acoustics, 6 \sqrt{5} might represent scaled intensities or pressures in sound waves or resonance phenomena. For example:

   
   $$ \text{Sound pressure: } P = 6 \sqrt{5} \times \text{base pressure} $$

   This helps in quantifying sound levels and their impact in different environments.

6. Quantum Mechanics:

   In quantum mechanics, 6 \sqrt{5} can appear in the scaling of wave functions, probabilities, or energy levels, particularly in systems involving irrational lengths or scaling factors. For example:

   
   $$ \text{Energy level: } E_n = 6 \sqrt{5} \hbar \omega \left(n + \frac{1}{2}\right) $$

   Such scaling allows for precise adjustment of quantum properties and behaviors.

The expression 6 \sqrt{5} plays a crucial role in physics and engineering, providing a means to scale, adjust, and interpret various quantities and phenomena, enhancing the understanding and application of mathematical principles in practical contexts.

Visualizing \( 6\sqrt{5} \) can be approached through several geometric and algebraic methods:

1. Geometric Representation: Represent \( 6\sqrt{5} \) as the hypotenuse of a right triangle with legs of lengths 6 and \( \sqrt{5} \).
2. Graphical Interpretation: Plotting \( y = 6\sqrt{x} \) on a Cartesian plane helps visualize the function's behavior.
3. Comparison with Known Values: Compare \( 6\sqrt{5} \) with other known quantities, such as integers and other irrational numbers, to grasp its magnitude.
4. Physical Models: Construct physical models or diagrams to illustrate the concept of \( 6\sqrt{5} \) in real-world contexts.

There are several misconceptions surrounding \( 6\sqrt{5} \) that are important to clarify:

1. Confusion with Exact Value: Some may mistakenly assume \( 6\sqrt{5} \) is a rational number or has a simple exact decimal value, whereas it is an irrational number.
2. Equation Misinterpretation: Incorrectly applying algebraic operations or equations involving \( 6\sqrt{5} \) without understanding its properties can lead to errors.
3. Scale and Context: Misjudging the magnitude or relevance of \( 6\sqrt{5} \) in various mathematical or practical contexts due to its specific numerical value.
4. Application Misunderstandings: Assuming \( 6\sqrt{5} \) behaves identically to other square roots or integers in calculations or applications where its unique properties matter.

Here are some common questions and answers about \( 6\sqrt{5} \):

1. What is \( 6\sqrt{5} \)?
   \( 6\sqrt{5} \) is an irrational number approximately equal to 13.41640786. It is the product of 6 and the square root of 5.
2. Is \( 6\sqrt{5} \) a rational or irrational number?
   \( 6\sqrt{5} \) is an irrational number because it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
3. How is \( 6\sqrt{5} \) used in mathematics?
   \( 6\sqrt{5} \) appears in various mathematical contexts such as geometry, algebra, and calculus. It is often used in calculations involving triangles and in equations where irrational numbers are necessary.
4. What are the properties of \( 6\sqrt{5} \)?
   \( 6\sqrt{5} \) is positive, irrational, and greater than 10 but less than 15. It is approximately 13.41640786 in decimal form.
5. Can \( 6\sqrt{5} \) be simplified further?
   No, \( 6\sqrt{5} \) is already in its simplest form as an expression involving a constant (6) and an irrational square root (5).