Square Root of 50 Simplified: Easy Steps to Master Radical Expressions

When simplifying the square root of 50, we aim to express it in its simplest radical form. Here's a step-by-step process:

Step-by-Step Simplification

1. Find the prime factors of 50. The prime factors are 2 and 5, as \(50 = 2 \times 5^2\).
2. Rewrite the square root of 50 using these prime factors:

   
   \[
   \sqrt{50} = \sqrt{2 \times 5^2}
   \]

3. Use the property of square roots that states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   
   \[
   \sqrt{50} = \sqrt{2} \times \sqrt{5^2}
   \]

4. Simplify \(\sqrt{5^2}\) to 5:

   
   \[
   \sqrt{50} = \sqrt{2} \times 5
   \]

5. Rearrange to get the final simplified form:

   
   \[
   \sqrt{50} = 5\sqrt{2}
   \]

Conclusion

The simplified form of the square root of 50 is \(5\sqrt{2}\). This expresses the square root in its simplest radical form.

The square root is a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\). Understanding square roots is essential for solving various mathematical problems and simplifying expressions.

Here are some key points about square roots:

• The square root of a number \(x\) is denoted as \(\sqrt{x}\).
• Square roots can be positive or negative, but the principal square root is always non-negative.
• Every positive number has two square roots: one positive and one negative. For instance, the square roots of 9 are 3 and -3.
• The square root of 0 is 0.

Simplifying square roots involves expressing the square root in its simplest radical form. This often requires prime factorization and the use of properties of square roots. Let's explore how to simplify the square root of 50.

1. Identify the prime factors of 50:
   • 50 can be factored into \(2 \times 25\).
   • 25 can be further factored into \(5 \times 5\).
2. Rewrite the square root of 50 using its prime factors:

   
   \[
   \sqrt{50} = \sqrt{2 \times 5^2}
   \]

3. Apply the property of square roots \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   
   \[
   \sqrt{50} = \sqrt{2} \times \sqrt{5^2}
   \]

4. Simplify \(\sqrt{5^2}\) to 5:

   
   \[
   \sqrt{50} = \sqrt{2} \times 5
   \]

5. Express the final simplified form:

   
   \[
   \sqrt{50} = 5\sqrt{2}
   \]

By following these steps, you can simplify the square root of 50 and apply similar techniques to other square roots. This foundational knowledge will help you tackle more complex mathematical problems with confidence.

Square roots are a crucial concept in mathematics, involving the process of determining a value which, when multiplied by itself, equals the original number. This value is called the square root. For instance, since \(7 \times 7 = 49\), we say that the square root of 49 is 7, written as \(\sqrt{49} = 7\).

Here are some important aspects of square roots:

• Notation: The square root of a number \(x\) is represented as \(\sqrt{x}\).
• Principal Square Root: By convention, \(\sqrt{x}\) denotes the principal (non-negative) square root.
• Positive and Negative Roots: While \(\sqrt{x}\) is non-negative, the equation \(x^2 = y\) has two solutions: \(x\) and \(-x\). For example, both 4 and -4 are square roots of 16.
• Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares, meaning their square roots are whole numbers.

To delve deeper, let's consider the process of finding and simplifying square roots:

1. Prime Factorization: Break down the number into its prime factors.

   For example, the prime factorization of 50 is:
   \[
   50 = 2 \times 5 \times 5 = 2 \times 5^2
   \]

2. Apply the Square Root: Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).

   This gives us:
   \[
   \sqrt{50} = \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}
   \]

3. Simplify: Recognize that \(\sqrt{5^2} = 5\), so:

   
   \[
   \sqrt{50} = \sqrt{2} \times 5 = 5\sqrt{2}
   \]

Understanding these principles allows you to simplify square roots effectively, whether they are perfect squares or not. Mastery of square roots is fundamental in algebra, geometry, and higher-level mathematics, providing a solid foundation for more complex problem-solving.

The square root of a number is a value that, when multiplied by itself, yields the original number. For example, since \(6 \times 6 = 36\), the square root of 36 is 6, denoted as \(\sqrt{36} = 6\).

Below are key definitions and properties of square roots:

• Notation: The square root of a number \(x\) is written as \(\sqrt{x}\).
• Principal Square Root: The principal square root is the non-negative square root. For any positive number \(x\), the principal square root is denoted by \(\sqrt{x}\) and is always positive.
• Positive and Negative Roots: Every positive number \(x\) has two square roots: \(\sqrt{x}\) and \(-\sqrt{x}\). For example, both 4 and -4 are square roots of 16 because \(4^2 = 16\) and \((-4)^2 = 16\).
• Zero: The square root of 0 is 0, as \(0 \times 0 = 0\).
• Imaginary Numbers: Negative numbers do not have real square roots. For example, \(\sqrt{-9}\) is not a real number, but can be expressed as an imaginary number: \(3i\), where \(i\) is the imaginary unit with the property \(i^2 = -1\).

Let's explore some important properties of square roots:

1. Product Property: The square root of a product is the product of the square roots:

   
   \[
   \sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
   \]

2. Quotient Property: The square root of a quotient is the quotient of the square roots:

   
   \[
   \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
   \]

3. Power Property: The square root of a number squared is the absolute value of the number:

   
   \[
   \sqrt{x^2} = |x|
   \]

4. Rational and Irrational Numbers: The square root of a rational number that is not a perfect square is an irrational number. For instance, \(\sqrt{2}\) is irrational.
5. Addition and Subtraction: Square roots cannot be directly added or subtracted unless they are like terms:

   
   \[
   \sqrt{a} + \sqrt{a} = 2\sqrt{a}, \quad \sqrt{a} + \sqrt{b} \neq \sqrt{a+b}
   \]

Understanding these definitions and properties helps in simplifying and manipulating square roots in various mathematical contexts. For example, simplifying the square root of 50 involves recognizing it as \(5\sqrt{2}\) through prime factorization and application of these properties.

Simplifying square roots involves expressing a square root in its simplest form. This process makes it easier to work with square roots in equations and calculations. The goal is to break down the square root into a product of simpler square roots, ideally involving perfect squares.

Here are the steps to simplify square roots:

1. Identify the Prime Factors: Determine the prime factors of the number under the square root.

   For example, for the number 50:
   \[
   50 = 2 \times 25 = 2 \times 5^2
   \]

2. Rewrite the Square Root: Express the square root as a product of the square roots of its prime factors.

   Using the example above:
   \[
   \sqrt{50} = \sqrt{2 \times 5^2}
   \]

3. Apply the Product Property: Utilize the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to separate the factors.

   Continuing with the example:
   \[
   \sqrt{50} = \sqrt{2} \times \sqrt{5^2}
   \]

4. Simplify the Perfect Squares: Recognize and simplify the square roots of perfect squares.

   In this case, \(\sqrt{5^2} = 5\), so:
   \[
   \sqrt{50} = \sqrt{2} \times 5 = 5\sqrt{2}
   \]

By following these steps, you can simplify square roots efficiently. This method can be applied to any number, allowing you to break down even the most complex square roots into simpler, more manageable forms.

Here are some additional examples to illustrate the process:

• Example 1: Simplify \(\sqrt{72}\).

  Prime factorization:
  \[
  72 = 2^3 \times 3^2
  \]
  Simplify:
  \[
  \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^2 \times 2 \times 3^2} = \sqrt{2^2} \times \sqrt{2} \times \sqrt{3^2} = 2 \times \sqrt{2} \times 3 = 6\sqrt{2}
  \]

• Example 2: Simplify \(\sqrt{18}\).

  Prime factorization:
  \[
  18 = 2 \times 3^2
  \]
  Simplify:
  \[
  \sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2}
  \]

Understanding the concept of simplifying square roots is a valuable skill in mathematics, making it easier to work with and manipulate square roots in various mathematical problems and equations.

The prime factorization method is a systematic approach to simplifying square roots by breaking down the number into its prime factors. This method leverages the properties of square roots and perfect squares to simplify expressions efficiently.

Here are the steps to simplify a square root using the prime factorization method:

1. Find the Prime Factors: Determine the prime factors of the number under the square root.

   For example, consider the number 50:
   \[
   50 = 2 \times 25 = 2 \times 5^2
   \]

2. Express the Number as a Product of Prime Factors: Write the number under the square root as a product of its prime factors.

   Using our example:
   \[
   \sqrt{50} = \sqrt{2 \times 5^2}
   \]

3. Separate the Square Root: Apply the property of square roots that allows you to separate the factors under the root.

   In this case:
   \[
   \sqrt{50} = \sqrt{2} \times \sqrt{5^2}
   \]

4. Simplify the Perfect Squares: Simplify any perfect squares under the square root.

   Here, \(\sqrt{5^2}\) simplifies to 5:
   \[
   \sqrt{50} = \sqrt{2} \times 5
   \]

5. Combine the Factors: Multiply the simplified square root by the remaining factors.

   Thus, the simplified form of \(\sqrt{50}\) is:
   \[
   \sqrt{50} = 5\sqrt{2}
   \]

Using the prime factorization method simplifies the process of handling square roots. Let's look at another example to reinforce this method:

• Example: Simplify \(\sqrt{72}\).
  1. Prime factorization:

     
     \[
     72 = 2^3 \times 3^2
     \]

  2. Express as a product of prime factors:

     
     \[
     \sqrt{72} = \sqrt{2^3 \times 3^2}
     \]

  3. Separate the square root:

     
     \[
     \sqrt{72} = \sqrt{2^3} \times \sqrt{3^2}
     \]

  4. Simplify the perfect squares:

     
     \[
     \sqrt{2^3} = \sqrt{2^2 \times 2} = \sqrt{2^2} \times \sqrt{2} = 2\sqrt{2}
     \]
     \[
     \sqrt{3^2} = 3
     \]

  5. Combine the factors:

     
     \[
     \sqrt{72} = 2\sqrt{2} \times 3 = 6\sqrt{2}
     \]

By following these steps, you can simplify any square root using the prime factorization method, making it a valuable tool in your mathematical toolkit.

Simplifying the square root of 50 involves breaking it down into its simplest form using prime factorization. Here is a detailed, step-by-step guide to simplify \(\sqrt{50}\).

1. Prime Factorization: Begin by finding the prime factors of 50.

   50 can be written as:
   \[
   50 = 2 \times 25
   \]
   Since 25 is a perfect square, we can further break it down:
   \[
   25 = 5 \times 5 = 5^2
   \]
   So, the prime factorization of 50 is:
   \[
   50 = 2 \times 5^2
   \]

2. Express Under the Square Root: Write the number under the square root using its prime factors.

   This gives us:
   \[
   \sqrt{50} = \sqrt{2 \times 5^2}
   \]

3. Separate the Square Root: Use the property of square roots that allows us to separate the factors.

   We apply:
   \[
   \sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
   \]
   So:
   \[
   \sqrt{50} = \sqrt{2} \times \sqrt{5^2}
   \]

4. Simplify the Perfect Square: Recognize and simplify the square root of the perfect square.

   Since \(\sqrt{5^2} = 5\), we have:
   \[
   \sqrt{50} = \sqrt{2} \times 5
   \]

5. Combine the Terms: Multiply the simplified square root by the remaining factors to get the final simplified form.

   This results in:
   \[
   \sqrt{50} = 5\sqrt{2}
   \]

By following these steps, you have successfully simplified \(\sqrt{50}\) to \(5\sqrt{2}\). This method can be applied to other numbers as well, allowing you to simplify square roots effectively.

Let's look at another example to reinforce this process:

• Example: Simplify \(\sqrt{72}\).
  1. Prime factorization:

     
     \[
     72 = 2^3 \times 3^2
     \]

  2. Express under the square root:

     
     \[
     \sqrt{72} = \sqrt{2^3 \times 3^2}
     \]

  3. Separate the square root:

     
     \[
     \sqrt{72} = \sqrt{2^3} \times \sqrt{3^2}
     \]

  4. Simplify the perfect squares:

     
     \[
     \sqrt{2^3} = \sqrt{2^2 \times 2} = \sqrt{2^2} \times \sqrt{2} = 2\sqrt{2}
     \]
     \[
     \sqrt{3^2} = 3
     \]

  5. Combine the terms:

     
     \[
     \sqrt{72} = 2\sqrt{2} \times 3 = 6\sqrt{2}
     \]

These examples illustrate how the prime factorization method simplifies square roots, making complex calculations more manageable.

There are several alternative methods to simplify square roots beyond the prime factorization method. Here, we will explore three popular methods: the approximation method, using a calculator, and recognizing perfect square factors.

1. Approximation Method

This method involves estimating the square root by finding two consecutive perfect squares between which the number lies.

1. Identify the two perfect squares that the number falls between. For √50, these are 49 (√49 = 7) and 64 (√64 = 8).
2. Since 50 is closer to 49, we can start with 7 and refine our estimate.
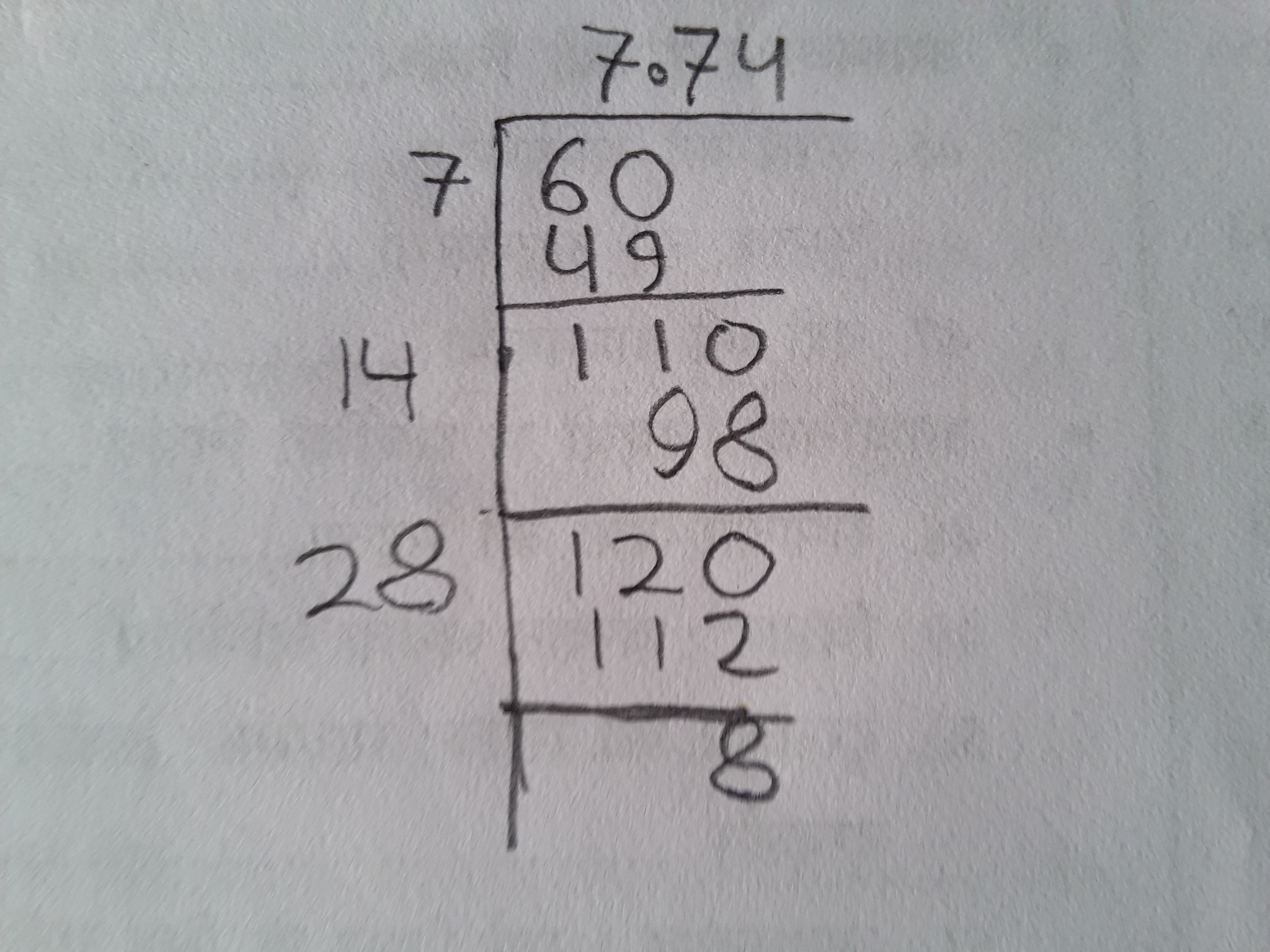
3. Using interpolation, we can estimate √50 to be approximately 7.07.

2. Using a Calculator

This is the most straightforward method, where you use a scientific calculator to find the square root directly.

1. Enter the number (50) into the calculator.
2. Press the square root (√) button to get the result.
3. The calculator will display √50 ≈ 7.07106781187.

3. Recognizing Perfect Square Factors

This method involves identifying if the number can be broken down into a product of a perfect square and another number.

1. Write the number under the square root as a product of its factors: √50 = √(25 × 2).
2. Recognize that 25 is a perfect square (5²).
3. Separate the factors: √(25 × 2) = √25 × √2.
4. Simplify the perfect square: √25 = 5, so the expression becomes 5√2.
5. Thus, √50 simplifies to 5√2.

These methods offer different ways to approach simplifying square roots, whether through estimation, direct calculation, or factorization.

Understanding how to simplify square roots can be extended to various numbers. Below are examples of simplifying different square roots step-by-step using the prime factorization method:

• Square Root of 32:
  1. Prime factorize 32: \(32 = 2 \times 2 \times 2 \times 2 \times 2\)
  2. Group the prime factors in pairs: \(\sqrt{32} = \sqrt{(2 \times 2) \times (2 \times 2) \times 2} = \sqrt{4 \times 4 \times 2}\)
  3. Take the square root of each pair: \(\sqrt{4} = 2\)
  4. Combine the results: \(2 \times 2 \times \sqrt{2} = 4\sqrt{2}\)

  So, \(\sqrt{32} = 4\sqrt{2}\).

• Square Root of 75:
  1. Prime factorize 75: \(75 = 3 \times 5 \times 5\)
  2. Group the prime factors in pairs: \(\sqrt{75} = \sqrt{3 \times (5 \times 5)} = \sqrt{3 \times 25}\)
  3. Take the square root of the perfect square: \(\sqrt{25} = 5\)
  4. Combine the results: \(5\sqrt{3}\)

  So, \(\sqrt{75} = 5\sqrt{3}\).

• Square Root of 18:
  1. Prime factorize 18: \(18 = 2 \times 3 \times 3\)
  2. Group the prime factors in pairs: \(\sqrt{18} = \sqrt{2 \times (3 \times 3)} = \sqrt{2 \times 9}\)
  3. Take the square root of the perfect square: \(\sqrt{9} = 3\)
  4. Combine the results: \(3\sqrt{2}\)

  So, \(\sqrt{18} = 3\sqrt{2}\).

• Square Root of 45:
  1. Prime factorize 45: \(45 = 3 \times 3 \times 5\)
  2. Group the prime factors in pairs: \(\sqrt{45} = \sqrt{(3 \times 3) \times 5} = \sqrt{9 \times 5}\)
  3. Take the square root of the perfect square: \(\sqrt{9} = 3\)
  4. Combine the results: \(3\sqrt{5}\)

  So, \(\sqrt{45} = 3\sqrt{5}\).

By following these steps, you can simplify various square roots effectively. Simplifying square roots helps in performing arithmetic operations more easily and avoiding errors in calculations.

When simplifying square roots, it is easy to make mistakes that can lead to incorrect answers. Here are some common pitfalls to watch out for:

• Incorrect Prime Factorization: Ensure that the number is correctly broken down into its prime factors. For example, the prime factorization of 50 is \(2 \times 5^2\). Incorrect factorization can lead to wrong simplification results.
• Missing Perfect Squares: Identify and factor out the largest perfect square from the number. Missing this step can result in an unsimplified or incorrectly simplified form. For instance, \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\).
• Ignoring Simplification: Always simplify the square root to its simplest form. \(\sqrt{50}\) should be simplified to \(5\sqrt{2}\), not left as \(\sqrt{50}\).
• Mistaking Rational and Irrational Numbers: Understand that the square root of a non-perfect square, like 50, is irrational and cannot be exactly represented as a simple fraction. \(\sqrt{50} \approx 7.071\) but is more accurately \(5\sqrt{2}\).
• Arithmetic Errors: Be cautious with calculations involving square roots. Incorrect arithmetic operations can lead to wrong results, especially in steps involving multiplication or division with the simplified form.

By avoiding these common mistakes, you can ensure accurate and simplified results when working with square roots.

Square roots have a wide range of practical applications across various fields. Here are some examples demonstrating their use:

1. Architecture

In architecture, square roots are used to calculate the dimensions and stability of structures. For instance, determining the natural frequency of buildings and bridges involves using square roots to ensure they can withstand vibrations from wind or traffic.

2. Finance

In finance, square roots are used to calculate stock market volatility. The standard deviation, a key measure of investment risk, is found by taking the square root of the variance of stock returns.

3. Physics

In physics, square roots are crucial in formulas involving motion and forces. For example, the formula for the time it takes an object to fall a certain distance under gravity involves the square root of the height.

\[
t = \frac{\sqrt{h}}{4}
\]

4. Electrical Engineering

Electrical engineers use square roots to calculate power, voltage, and current in circuits. For example, the root mean square (RMS) value of an alternating current (AC) is found using the square root of the average of the squares of the current values.

5. Statistics

In statistics, the standard deviation, which measures the dispersion of a data set, is the square root of the variance. This helps in understanding the spread and distribution of data.

6. Geometry

In geometry, square roots are used to calculate the side lengths of squares and the hypotenuse of right triangles using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]

7. Computer Science

In computer science, square roots are used in algorithms for encryption, image processing, and game physics. For example, calculating distances between points in graphics involves the square root of the sum of the squares of the differences in coordinates.

8. Navigation

Pilots and navigators use square roots to calculate distances between points on a map. This is essential for plotting courses and estimating travel times.

9. Accident Investigations

Police officers use square roots to determine the speed of a vehicle before an accident based on the length of skid marks:
\[
\text{Speed} = \sqrt{24 \times \text{skid length}}
\]

10. Cooking

In cooking, scaling recipes up or down can involve square roots to maintain the correct proportions of ingredients. This is particularly useful when adjusting quantities for larger or smaller servings.

11. Photography

The f-number of a camera lens, which affects exposure, is based on the square root of the aperture area. Changing the f-number by a factor of two changes the amount of light entering the camera by a factor of four.

These examples highlight the versatility and importance of understanding and using square roots in practical situations.

For those looking to deepen their understanding of square roots, including the simplification process and practical applications, here are some valuable resources:

• Mathstoon: Simplified Square Root of 50

  This comprehensive guide covers the definition, properties, and methods for simplifying square roots, with a focus on the square root of 50.

• BYJU's: Square Root of 50

  Explore detailed explanations and methods for finding and simplifying square roots, including step-by-step instructions for the square root of 50.

• Mathometrics: Square Root of 50

  Discover various methods for calculating the square root of 50, including prime factorization and long division, and learn about its applications and significance.

• Khan Academy: Radical Expressions

  A great resource for learning about radical expressions, including simplifying square roots, with interactive exercises and video tutorials.

• Wolfram Alpha: Square Root Calculator

  Use this powerful calculator to find the square roots of any number, including detailed steps for simplification and other mathematical insights.

These resources provide a robust foundation for mastering the concept of square roots and their simplification, offering both theoretical knowledge and practical tools.