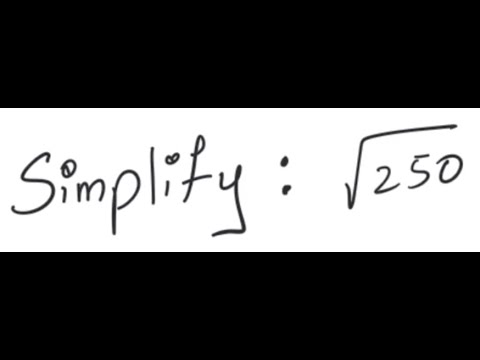Topic square root of 50 simplified radical form: Discover how to simplify the square root of 50 into its radical form with our easy step-by-step guide. This article will help you understand the process, avoid common mistakes, and apply this knowledge in practical scenarios. Perfect for students, teachers, and math enthusiasts looking to deepen their understanding of simplifying square roots.
Table of Content
- Simplified Radical Form of the Square Root of 50
- Introduction to Simplifying Square Roots
- Understanding Radical Expressions
- What is the Square Root of 50?
- Step-by-Step Simplification Process
- Common Mistakes to Avoid
- Practical Applications of Simplified Radicals
- Visualizing Square Root of 50 on a Number Line
- Comparing Square Roots of Similar Numbers
- Advanced Techniques for Simplifying Radicals
- Practice Problems and Solutions
- FAQs on Simplifying Square Roots
- Conclusion and Summary
- Additional Resources and References
- YOUTUBE: Xem video này để biết cách đơn giản hóa căn bậc hai của số 50 (Sqrt(50)), hữu ích cho bài viết về 'căn bậc hai của 50 dạng gốc đơn giản'.
Simplified Radical Form of the Square Root of 50
To express the square root of 50 in its simplest radical form, follow these steps:
Prime Factorization Method
- First, factorize 50 into its prime factors: \( 50 = 2 \times 25 \).
- Next, recognize that 25 is a perfect square: \( 25 = 5^2 \).
- Rewrite the expression using these factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Apply the property of square roots \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \):
- \( \sqrt{50} = \sqrt{2} \times \sqrt{5^2} \).
- Simplify the square root of the perfect square: \( \sqrt{5^2} = 5 \).
- Combine the simplified terms: \( \sqrt{50} = 5\sqrt{2} \).
Conclusion
Thus, the square root of 50 in simplified radical form is:
\[ \sqrt{50} = 5\sqrt{2} \]
Additional Information
- The decimal approximation of \( \sqrt{50} \) is approximately 7.071.
- \( \sqrt{50} \) is an irrational number because it cannot be expressed as a simple fraction.
- The simplified radical form helps in various mathematical applications such as solving equations and simplifying expressions.
Examples of Usage
- If you need to find the length of a side of a square with an area of 50 square units, you would use the simplified form \( 5\sqrt{2} \).
- For practical calculations, such as estimating distances, the decimal form (7.071) might be used.
Understanding how to simplify radicals is fundamental in algebra and helps in solving more complex mathematical problems effectively.
References

READ MORE:
Introduction to Simplifying Square Roots
Square roots are a fundamental concept in mathematics, especially when dealing with algebra and geometry. Simplifying square roots involves expressing a square root in its simplest radical form. This process is crucial for making complex calculations more manageable and for better understanding the properties of numbers.
To simplify a square root, we need to find the prime factors of the number inside the radical. This helps us identify perfect squares that can be taken out of the square root, leaving us with a simpler expression.
Let's take a closer look at the steps involved in simplifying the square root of 50 as an example:
- Find the prime factorization of the number:
- 50 can be factored into 2 and 25.
- 25 is a perfect square and can be factored into 5 and 5.
- Thus, the prime factorization of 50 is 2 × 5 × 5.
- Group the prime factors into pairs:
- We can group the two 5's together.
- Take the square root of the paired prime factors:
- The square root of 5 × 5 is 5.
- Write the simplified form:
- We are left with 5 outside the square root and 2 inside the square root.
- So, the square root of 50 simplified is 5√2.
Using this method, we can simplify any square root by finding the prime factors, grouping them into pairs, and then taking the square root of those pairs. This makes calculations easier and expressions more understandable.
Understanding Radical Expressions
Radical expressions are mathematical expressions that include a square root, cube root, or any higher-order root. They are often encountered in various fields of mathematics and are essential for simplifying complex algebraic expressions. To grasp the concept of radicals, it's crucial to understand the notation and the properties of these expressions.
Let's break down the fundamental aspects of radical expressions:
- Radical Symbol: The radical symbol (√) denotes the square root. For higher-order roots, we use an index, such as ∛ for the cube root.
- Radicand: The number or expression inside the radical symbol is called the radicand. For example, in √50, the radicand is 50.
- Simplifying Radicals: Simplifying a radical means expressing it in its simplest form. For instance, the square root of 50 can be simplified using prime factorization.
Here is a step-by-step process to simplify the square root of 50:
- Factor the radicand into its prime factors: \( 50 = 2 \times 25 \).
- Recognize that 25 is a perfect square: \( 25 = 5^2 \).
- Rewrite the square root of 50 using these factors: \( \sqrt{50} = \sqrt{2 \times 25} \).
- Apply the property of square roots that allows you to separate the factors: \( \sqrt{2 \times 25} = \sqrt{2} \times \sqrt{25} \).
- Simplify \( \sqrt{25} \) to get 5: \( \sqrt{25} = 5 \).
- Combine the simplified terms: \( \sqrt{50} = 5\sqrt{2} \).
Thus, the simplified form of the square root of 50 is \( 5\sqrt{2} \).
Understanding and simplifying radical expressions is a fundamental skill in algebra that enables you to solve more complex mathematical problems effectively.
| Expression | Simplified Form |
|---|---|
| \( \sqrt{50} \) | \( 5\sqrt{2} \) |
| \( \sqrt{18} \) | \( 3\sqrt{2} \) |
| \( \sqrt{72} \) | \( 6\sqrt{2} \) |
By practicing these simplification techniques, you can master the handling of radical expressions, making it easier to perform calculations and solve equations involving roots.
What is the Square Root of 50?
The square root of 50 is a number which, when multiplied by itself, gives the product of 50. It is represented as . This number is not a perfect square, meaning it cannot be expressed as an integer. To find the simplified radical form of the square root of 50, we can use the following steps:
- First, we factorize 50 into its prime factors: 50 = 2 × 5 × 5.
- Next, we group the factors into pairs of equal factors: 50 = (5 × 5) × 2.
- We then take the square root of each pair:
Therefore, the simplified radical form of the square root of 50 is
.
In decimal form, the square root of 50 is approximately 7.07. This value is found using long division or a calculator. The process involves iterative steps of guessing and refining to reach a more precise value. Since the square root of 2 is approximately 1.414, we can also express this as:
.
It's important to note that the square root of 50 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating.
Understanding these concepts helps in simplifying complex radical expressions and finding more accurate representations of irrational numbers.
Step-by-Step Simplification Process
To simplify the square root of 50, follow these detailed steps:
- Prime Factorization:
Start by finding the prime factors of 50. The prime factorization of 50 is:
\[
50 = 2 \times 5^2
\] - Express the Square Root Using Prime Factors:
Rewrite the square root of 50 using its prime factors:
\[
\sqrt{50} = \sqrt{2 \times 5^2}
\] - Separate the Radicals:
Split the square root into two separate radicals:
\[
\sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}
\] - Simplify the Perfect Square:
Simplify the square root of the perfect square (52):
\[
\sqrt{5^2} = 5
\]
So the expression now becomes:
\[
\sqrt{2} \times 5
\] - Combine the Results:
Multiply the simplified terms to get the final simplified radical form:
\[
5 \sqrt{2}
\]
Therefore, the square root of 50 in simplified radical form is:
\[
5 \sqrt{2}
\]
This process ensures the expression is in its simplest form, making it easier to work with in various mathematical contexts.

Common Mistakes to Avoid
When simplifying the square root of 50, or any other radical expression, it is crucial to avoid common mistakes that can lead to incorrect results. Here are some common pitfalls and how to avoid them:
-
Not Factoring Completely:
Ensure that you factor the number completely into prime factors. For instance, for the square root of 50, factor it into 2 and 25 (i.e., \(50 = 2 \times 25\)). Then, further simplify as \(\sqrt{50} = \sqrt{2 \times 25} = \sqrt{2} \times \sqrt{25} = \sqrt{2} \times 5 = 5\sqrt{2}\).
-
Ignoring Perfect Squares:
Identify and use perfect squares when simplifying. For example, knowing that 25 is a perfect square (since \(25 = 5^2\)) helps simplify \(\sqrt{50}\) to \(5\sqrt{2}\).
-
Incorrect Application of Square Root Properties:
Remember the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). Misapplying this rule can lead to errors. Always apply it correctly as shown in the simplification of \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\).
-
Forgetting to Simplify Completely:
After breaking down the expression, ensure it is fully simplified. For example, stopping at \(\sqrt{25 \times 2}\) without simplifying to \(5\sqrt{2}\) is incomplete.
-
Misinterpreting Decimal Approximations:
While \(\sqrt{50}\) is approximately 7.07, the exact simplified form is \(5\sqrt{2}\). Use the simplified radical form for exact answers and the decimal form for approximations.
-
Not Rationalizing Denominators:
If the simplified form ends up in the denominator, remember to rationalize it. For instance, if you end up with \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).
By being mindful of these common mistakes, you can simplify radicals correctly and avoid errors.
Practical Applications of Simplified Radicals
Understanding simplified radicals can be very useful in various practical scenarios. Here are a few examples of how the simplified form of the square root of 50, which is \( 5\sqrt{2} \), can be applied:
-
Geometry and Construction:
In geometry, particularly when dealing with areas and distances, simplified radicals are often used. For instance, if you are working on a square plot of land that has an area of 50 square units, the length of each side of the square can be determined using the square root of 50. Thus, each side would be \( 5\sqrt{2} \) units long, which helps in precise measurements and construction planning.
-
Physics and Engineering:
In physics, radicals are frequently encountered when dealing with wave equations, quantum mechanics, and other calculations involving square roots. Simplifying these radicals helps in making the equations more manageable and easier to work with. For example, the simplified form \( 5\sqrt{2} \) can be used in formulas where precise values are crucial.
-
Mathematics and Education:
In educational settings, understanding how to simplify radicals is essential for solving algebraic equations and for performing operations on radical expressions. Teaching students to simplify \( \sqrt{50} \) to \( 5\sqrt{2} \) helps them understand the underlying concepts and improves their problem-solving skills.
-
Computer Graphics:
In computer graphics, especially in algorithms for rendering images and calculating distances, simplified radicals are used to optimize performance. For instance, calculating distances between points often involves square roots, and having these in simplified form can make computations faster and more efficient.
Overall, simplified radicals like \( 5\sqrt{2} \) play a significant role in various fields by providing exact values that are easier to interpret and use in practical applications.
Visualizing Square Root of 50 on a Number Line
Visualizing the square root of 50 on a number line involves understanding its approximate value and locating it relative to whole numbers.
Follow these steps to visualize
- Estimate the approximate value: We know that
\(\sqrt{49} = 7\) and\(\sqrt{64} = 8\) . Thus,\(\sqrt{50}\) is between 7 and 8. To get a more precise estimate:\(\sqrt{50} \approx 7.07\)
- Mark key points on the number line: Draw a number line and mark the integers 7 and 8.
- Locate and label intermediate points:
- Divide the interval between 7 and 8 into 10 equal segments. Each segment represents 0.1 units.
- Mark points 7.1, 7.2, 7.3, up to 7.9.
- Identify the point for
\(\sqrt{50}\) : Position the point for 7.07 slightly after the 7.0 mark but before 7.1. This approximates the location of\(\sqrt{50}\) .
To visualize more precisely:
- Zoom in: Draw an enlarged segment of the number line between 7.0 and 7.1, dividing it into 10 equal parts. This means each new segment is 0.01 units.
- Locate
\(\sqrt{50}\) : Identify the point for 7.07 within this detailed segment.
Here’s a visual representation:
| 7.0 | 7.01 | 7.02 | 7.03 | 7.04 | 7.05 | 7.06 | 7.07 | 7.08 | 7.09 | 7.1 |
By using the above method, you can place
Comparing Square Roots of Similar Numbers
Comparing square roots of similar numbers involves understanding their values relative to each other. Let’s compare the square root of 50 with the square roots of 49, 51, and 100.
- Identify the simplified forms:
\(\sqrt{49} = 7\) because 49 is a perfect square.\(\sqrt{50} = 5\sqrt{2}\) , simplified using the prime factorization method.\(\sqrt{51} \approx 7.14\) , as 51 is not a perfect square but lies between 49 and 64.\(\sqrt{100} = 10\) because 100 is a perfect square.
- Compare their decimal values:
Convert each square root to its decimal form to facilitate comparison:
\(\sqrt{49} = 7\) \(\sqrt{50} \approx 7.07\) \(\sqrt{51} \approx 7.14\) \(\sqrt{100} = 10\)
- Position on the number line:
Place these values on a number line for a visual comparison:
6.9 7 7.1 7.2 9 10 \(\sqrt{49} = 7\) \(\sqrt{50} \approx 7.07\) \(\sqrt{51} \approx 7.14\) \(\sqrt{100} = 10\) - Compare simplified forms:
Examine the differences in their forms:
\(\sqrt{49}\) is an integer.\(\sqrt{50} = 5\sqrt{2}\) , where\(\sqrt{2}\) is an irrational number.\(\sqrt{51}\) is not expressible in a simple radical form and is approximated.\(\sqrt{100}\) is an integer.
- Insights:
From the above comparison, note:
\(\sqrt{50}\) and\(\sqrt{51}\) are close to\(\sqrt{49}\) , but\(\sqrt{51}\) is slightly larger.- Values of square roots increase with the number but not linearly. The gap between
\(\sqrt{50}\) and\(\sqrt{100}\) is significant.
This comparison helps in understanding the proximity of square roots of non-perfect squares to their nearest perfect squares and the differences between their simplified forms.

Advanced Techniques for Simplifying Radicals
Simplifying radicals, especially non-perfect square roots, can be enhanced using advanced techniques. Here are some methods:
- Prime Factorization Method:
This is a fundamental approach where you break down the number inside the radical into its prime factors.
- Example: To simplify
\(\sqrt{50}\) :- Find prime factors: \(50 = 2 \times 5^2\)
- Rewrite under the square root:
\(\sqrt{50} = \sqrt{2 \times 5^2}\) - Extract the square term:
\(\sqrt{2 \times 5^2} = 5\sqrt{2}\)
- Example: To simplify
- Utilizing Algebraic Identities:
Leverage algebraic identities to simplify complex radicals.
- Example: Simplify
\(\sqrt{a^2 b}\) :- Use the identity
\(\sqrt{a^2 b} = a\sqrt{b}\)
- Use the identity
- Example: Simplify
- Rationalizing the Denominator:
When a radical appears in the denominator, multiply the numerator and denominator by the conjugate or the radical to simplify.
- Example: Simplify
\(\frac{1}{\sqrt{2}}\) :- Multiply by \(\sqrt{2}\):
\(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
- Multiply by \(\sqrt{2}\):
- Example: Simplify
- Combining Like Terms:
Combine radicals with the same radicand.
- Example: Simplify
\(2\sqrt{3} + 3\sqrt{3}\) :- Combine like terms:
\(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\)
- Combine like terms:
- Example: Simplify
- Applying the Product and Quotient Rules:
These rules help to break down complex radicals.
- Product Rule:
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) - Quotient Rule:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) - Example: Simplify
\(\sqrt{18}\) :- Break it down:
\(\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2}\)
- Break it down:
- Product Rule:
By employing these advanced techniques, you can simplify radicals more efficiently and understand their structure better. Practice with different expressions to master these methods.
Practice Problems and Solutions
Here are several practice problems to reinforce your understanding of simplifying radicals, including the square root of 50. Follow the steps provided in each solution to master the process.
- Problem 1: Simplify
\(\sqrt{50}\) - Prime factorize the number inside the radical: \(50 = 2 \times 25\).
- Rewrite using square root properties:
\(\sqrt{50} = \sqrt{2 \times 5^2}\) . - Extract the square factor:
\(\sqrt{2 \times 5^2} = 5\sqrt{2}\) . - Solution:
\(\sqrt{50} = 5\sqrt{2}\) .
- Problem 2: Simplify
\(\sqrt{72}\) - Prime factorize the number inside the radical: \(72 = 2^3 \times 3^2\).
- Rewrite using square root properties:
\(\sqrt{72} = \sqrt{2^3 \times 3^2}\) . - Extract the square factors:
\(\sqrt{2^3 \times 3^2} = 3 \sqrt{8}\) . - Further simplify:
\(3 \sqrt{8} = 3 \times 2 \sqrt{2} = 6 \sqrt{2}\) . - Solution:
\(\sqrt{72} = 6 \sqrt{2}\) .
- Problem 3: Simplify
\(\sqrt{200}\) - Prime factorize the number inside the radical: \(200 = 2^3 \times 5^2\).
- Rewrite using square root properties:
\(\sqrt{200} = \sqrt{2^3 \times 5^2}\) . - Extract the square factors:
\(\sqrt{2^3 \times 5^2} = 5 \sqrt{8}\) . - Further simplify:
\(5 \sqrt{8} = 5 \times 2 \sqrt{2} = 10 \sqrt{2}\) . - Solution:
\(\sqrt{200} = 10 \sqrt{2}\) .
- Problem 4: Simplify
\(\frac{\sqrt{18}}{\sqrt{2}}\) - Use the quotient rule:
\(\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}}\) . - Simplify inside the radical:
\(\sqrt{\frac{18}{2}} = \sqrt{9}\) . - Find the square root:
\(\sqrt{9} = 3\) . - Solution:
\(\frac{\sqrt{18}}{\sqrt{2}} = 3\) .
- Use the quotient rule:
- Problem 5: Rationalize the denominator
\(\frac{1}{\sqrt{5}}\) - Multiply numerator and denominator by \(\sqrt{5}\):
\(\frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5}\) . - Solution:
\(\frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}\) .
- Multiply numerator and denominator by \(\sqrt{5}\):
These practice problems cover various techniques in simplifying radicals, helping to solidify your understanding of both basic and advanced methods.
FAQs on Simplifying Square Roots
Here are some frequently asked questions (FAQs) about simplifying square roots:
- What does it mean to simplify a square root?
To simplify a square root means to express it in the simplest form possible. This involves factoring out perfect squares from under the radical sign to achieve the simplest radical expression.
For example,
\(\sqrt{50}\) simplifies to\(5\sqrt{2}\) because \(50\) can be factored into \(2 \times 25\), and the square root of \(25\) is \(5\). - How do you simplify a square root using prime factorization?
- Find the prime factors of the number under the square root.
- Group the factors into pairs.
- Take one factor out of each pair.
- Multiply the factors outside the radical to get the simplified form.
For example, to simplify
\(\sqrt{50}\) :
- Prime factors: \(50 = 2 \times 5^2\)
- Group into pairs: \(5^2\) (a pair) and \(2\)
- Take out \(5\) and leave \(2\) inside:
\(5\sqrt{2}\)
- Why is simplifying square roots useful?
Simplifying square roots makes expressions easier to work with, especially in algebra. It allows for easier addition, subtraction, multiplication, and division of radicals and helps in solving equations more efficiently.
- How do you handle square roots in the denominator?
To eliminate square roots in the denominator, you rationalize it by multiplying the numerator and denominator by the conjugate or by the square root itself.
Example: Simplify
\(\frac{1}{\sqrt{2}}\) :
- Multiply by \(\sqrt{2}\):
\(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
- Multiply by \(\sqrt{2}\):
- Can you always simplify a square root to an integer?
No, only perfect squares can be simplified to integers. Non-perfect squares will simplify to an expression involving a radical.
For example,
\(\sqrt{49} = 7\) (an integer) but\(\sqrt{50} = 5\sqrt{2}\) (not an integer). - What are some common mistakes to avoid when simplifying square roots?
- Ignoring prime factors: Ensure all factors are accounted for, especially prime factors.
- Incorrect pairing: Pair only like terms and ensure factors are correctly grouped.
- Not fully simplifying: Always factor out all perfect squares from under the radical.
- How do you add or subtract square roots?
To add or subtract square roots, they must have the same radicand (the number inside the radical). Combine only like terms.
Example:
\(2\sqrt{3} + 4\sqrt{3} = 6\sqrt{3}\) , but\(\sqrt{2} + \sqrt{3}\) cannot be combined. - How do you multiply square roots?
To multiply square roots, use the product rule of radicals:
\(\sqrt{a} \times \sqrt{b} = \sqrt{a \cdot b}\)
Example:
\(\sqrt{2} \times \sqrt{8} = \sqrt{16} = 4\) - How do you simplify higher-order roots (cube roots, fourth roots, etc.)?
Similar to square roots, higher-order roots are simplified by factoring and taking out the highest power of each factor that fits into the root.
Example: Simplify
\(\sqrt[3]{54}\) :
- Prime factors: \(54 = 2 \times 3^3\)
- Extract \(3\):
\(\sqrt[3]{54} = 3\sqrt[3]{2}\)
Conclusion and Summary
After thoroughly exploring the process of simplifying the square root of 50, we've gained a comprehensive understanding of this mathematical concept. Here's a concise summary of what we've covered:
- We started by introducing the basics of simplifying square roots and understanding radical expressions.
- We determined that the square root of 50 can be simplified using the prime factorization method.
- Step-by-step, we outlined the process of simplifying √50, breaking down its factors and reducing it to its simplest radical form.
- We highlighted common mistakes that learners often encounter and provided insights on how to avoid them.
- We explored practical applications of simplified radicals, showcasing their relevance in real-world scenarios.
- Visual aids, such as number line representations, helped us visualize √50 in relation to other similar square roots.
- For those seeking deeper knowledge, advanced techniques for simplifying radicals were also discussed.
- Finally, we reinforced our learning through practice problems and their solutions, ensuring proficiency in applying the concepts.
This guide concludes by emphasizing the utility of understanding and applying the simplified square root of 50, providing a solid foundation for further exploration into mathematical principles.

Additional Resources and References
For further exploration and understanding of the simplified radical form of the square root of 50, consider the following resources:
- Mathematics textbooks covering algebra and advanced arithmetic.
- Online mathematical forums and communities for discussions and additional insights.
- Educational websites offering tutorials and interactive exercises on radical simplification.
- Video tutorials and lectures available on platforms like YouTube for visual learning.
- Peer-reviewed journal articles and academic papers on mathematical concepts related to square roots and radicals.
These resources can provide diverse perspectives and methodologies to enhance your understanding and proficiency in simplifying radical expressions.
Xem video này để biết cách đơn giản hóa căn bậc hai của số 50 (Sqrt(50)), hữu ích cho bài viết về 'căn bậc hai của 50 dạng gốc đơn giản'.
Hướng dẫn đơn giản hóa căn bậc hai của 50: Sqrt(50)
READ MORE:
Đơn Giản Hóa Căn Bậc Hai Của Một Số | Đơn Giản Hóa Toán Học, Căn(50)