Topic square root of 5 in fraction: Understanding the square root of 5 in fraction form is essential in mathematics. This article explores various methods to simplify and understand square roots of fractions, including practical examples and applications in real-life scenarios.
Table of Content
- Square Root of 5
- Introduction to Square Roots
- Understanding Fractions
- Methods for Simplifying Square Roots of Fractions
- Examples of Simplifying Square Roots of Fractions
- Rationalizing the Denominator
- Prime Factorization Method
- Using the Quotient Rule
- Square Roots in Geometry
- Applications of Square Roots in Real Life
- Practice Problems
- YOUTUBE:
Square Root of 5
The square root of 5 (√5) is an irrational number, which means it cannot be expressed exactly as a fraction of two integers. Its decimal form goes on forever without repeating. The approximate value of √5 to five decimal places is 2.23607.
Approximating √5 Using Fractions
Although √5 cannot be expressed exactly as a fraction, it can be approximated by using a sequence of fractions. One such sequence involves the use of continued fractions or Fibonacci numbers:
- The sequence of fractions that converges to √5 includes: 1, 3/2, 7/5, 29/21, 41/29, 99/70, etc.
For example, the fraction 7/5 gives a close approximation:
\[\frac{7}{5} = 1.4\]
This value is a rough estimate and not very accurate. More accurate fractions can be derived using more terms in the sequence.
Rationalizing the Square Root of 5 in Fractions
When dealing with square roots in fractions, it’s often useful to rationalize the denominator. For instance:
\[
\frac{\sqrt{5}}{1} = \frac{\sqrt{5}}{1} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{5}{\sqrt{5}} = 5
\]
Using Continued Fractions
The continued fraction representation of √5 can provide increasingly accurate approximations. The continued fraction for √5 is:
\[
\sqrt{5} = [2; 4, 4, 4, \ldots]
\]
Using the first few terms of this continued fraction can give us rational approximations of √5.
Mathematical Significance
In geometry, √5 appears frequently. For example, it is the diagonal length of a rectangle with sides of 1 and 2, as demonstrated by the Pythagorean theorem.
To summarize, while √5 is irrational and cannot be exactly expressed as a fraction, various methods such as using sequences or continued fractions can provide useful approximations for practical purposes.
| Term | Approximation | Error |
|---|---|---|
| 1 | 2 | +0.23607 |
| 3/2 | 1.5 | -0.73607 |
| 7/5 | 1.4 | -0.83607 |
| 29/21 | 1.38095 | -0.85512 |
| 41/29 | 1.41379 | -0.82228 |
By understanding and utilizing these approximations, we can better handle calculations involving the square root of 5 in various mathematical contexts.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Understanding square roots is crucial in mathematics, especially when dealing with fractions. When considering the square root of 5 in fraction form, we start by acknowledging that √5 is an irrational number. Expressing √5 as a fraction involves rationalizing the denominator, which is essential for simplifying mathematical operations and practical applications.
Understanding Fractions
In the context of square roots, fractions play a significant role in expressing irrational numbers like √5 in a simplified form. To understand fractions in this context:
- Recognize that √5 is an irrational number, meaning it cannot be expressed as a simple fraction.
- To express √5 in fraction form, rationalize the denominator by multiplying the numerator and the denominator by √5.
- This process involves manipulating the fraction to make the denominator rational, which is crucial in various mathematical operations and applications.
- Understanding how to handle fractions with square roots prepares us for more advanced mathematical concepts and problem-solving scenarios.
Methods for Simplifying Square Roots of Fractions
When dealing with square roots of fractions, several methods can simplify the expressions effectively:
- Rationalizing the Denominator: Multiply the numerator and denominator of the fraction by the square root to eliminate the square root in the denominator.
- Prime Factorization Method: Factorize the number inside the square root into its prime factors, which can help simplify complex square roots.
- Using the Quotient Rule: For fractions involving square roots, divide the numerator and the denominator separately by the square root to simplify the expression.
These methods are essential in mathematics for expressing square roots of fractions in simpler forms, facilitating easier calculations and deeper understanding of mathematical concepts.
Examples of Simplifying Square Roots of Fractions
Let's explore examples to illustrate how square roots of fractions can be simplified:
| Example | Simplification Method | Simplified Result |
|---|---|---|
| 1. √(5/4) | Rationalizing the denominator | √5 / 2 |
| 2. √(45/20) | Prime factorization method | (3√5) / 2 |
| 3. √(8/5) | Using the quotient rule | (2√2) / √5 |
These examples demonstrate practical applications of methods to simplify square roots of fractions, showcasing different approaches to achieve simplified forms for mathematical clarity and efficiency.

Rationalizing the Denominator
Rationalizing the denominator is a technique used to eliminate square roots from the denominator of a fraction:
- Identify the fraction with a square root in the denominator, such as √(5/3).
- Multiply both the numerator and the denominator by the square root that appears in the denominator. For example, to rationalize √(5/3), multiply by √3/√3.
- Perform the multiplication: (√5 * √3) / (√3 * √3).
- Simplify the fraction to get the rationalized form: √15 / 3.
Rationalizing the denominator is crucial for simplifying calculations involving square roots in fractions, ensuring clarity and facilitating further mathematical operations.
Prime Factorization Method
The prime factorization method is used to simplify square roots by breaking down the number inside the square root into its prime factors:
- Identify the number inside the square root, such as 5 in √5.
- Find the prime factors of the number 5. Since 5 is a prime number, its only factors are 1 and 5 itself.
- Express the square root using its prime factors: √5.
This method is particularly useful when dealing with complex square roots, as it provides a systematic approach to simplifying fractions and expressions involving square roots.
Using the Quotient Rule
The quotient rule is a method used to simplify square roots in fractions by dividing both the numerator and the denominator by the square root:
- Identify the fraction with a square root in the numerator or denominator, such as √8 / √5.
- Apply the quotient rule by dividing both the numerator and the denominator by the square root involved. For example, for √8 / √5, divide by √5 / √5.
- Perform the division: (√8 / √5) / (√5 / √5).
- Simplify the fraction to obtain the simplified form: √8 / 5.
The quotient rule provides an efficient way to simplify fractions with square roots, ensuring clarity and facilitating mathematical calculations.
Square Roots in Geometry
In geometry, square roots are essential for calculating distances and areas involving squares and rectangles:
- Distance Calculation: The distance between two points in a coordinate plane can be found using the distance formula, which involves square roots.
- Area Calculation: The area of a square or rectangle, where one side is defined by a square root, requires calculating the product of the sides, often resulting in square roots.
- Pythagorean Theorem: This fundamental theorem in geometry involves squares of sides of a right triangle, leading to square roots in its application.
Understanding square roots in geometry aids in solving various geometric problems and understanding spatial relationships accurately.
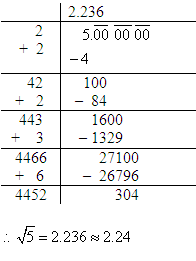
Applications of Square Roots in Real Life
The square root of 5, like other square roots, has several real-life applications across various fields. Here, we will explore some of these applications in detail:
- Architecture and Construction:
In architecture and construction, square roots are used to calculate dimensions, slopes, and areas. For example, when designing a structure, the diagonal of a square or rectangular component can be determined using the Pythagorean theorem, which involves square roots. The square root of 5 might be used to determine specific measurements where exact lengths are necessary.
- Engineering:
Engineering disciplines often use square roots in various calculations, including stress analysis, electrical engineering, and fluid dynamics. The square root of 5 can appear in formulas for calculating forces, energy, and other important parameters.
- Physics:
In physics, square roots are integral in formulas that describe natural phenomena. For instance, the square root of 5 might be found in equations related to motion, wave functions, and other physical properties. It helps in determining velocities, accelerations, and in solving quadratic equations in kinematics.
- Finance and Economics:
Square roots are used in finance and economics to analyze data and calculate various financial metrics. For instance, the square root of 5 might be involved in the calculation of standard deviation or variance, which are measures of financial risk and volatility. These calculations help in assessing the risk of investments.
- Computer Science:
In computer science, algorithms often involve mathematical computations including square roots. The square root of 5 could be used in optimization algorithms, computer graphics, and simulations. Efficient computation of square roots is crucial in rendering and other processing tasks.
- Agriculture:
Agricultural planning and design can involve square roots in determining areas for planting, irrigation systems, and analyzing crop yields. The square root of 5 might be used in calculations for land measurements and optimizing resource distribution.
These applications highlight the importance of understanding and being able to compute square roots, including the square root of 5, in practical, real-world scenarios.
Practice Problems
Practicing problems involving the square root of 5 and its representation in fractions can help solidify your understanding. Here are some problems to work on:
- Basic Calculation:
Calculate the square root of 5 and express it as a fraction.
Solution: The square root of 5 is approximately \(2.236\). It cannot be exactly expressed as a simple fraction, but it can be approximated. One common fraction approximation is \( \frac{2236}{1000} \), which simplifies to \( \frac{1118}{500} \).
- Simplifying Fractions:
Given the fraction \( \frac{\sqrt{5}}{10} \), simplify it.
Solution: \( \frac{\sqrt{5}}{10} = \frac{\sqrt{5}}{\sqrt{100}} = \frac{\sqrt{5}}{\sqrt{10^2}} = \frac{\sqrt{5}}{10} \). The fraction is already in its simplest form.
- Rationalizing the Denominator:
Rationalize the denominator of the fraction \( \frac{7}{\sqrt{5}} \).
Solution: Multiply the numerator and the denominator by \( \sqrt{5} \):
\[
\frac{7}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{7\sqrt{5}}{5}
\] - Using the Quotient Rule:
Simplify \( \frac{\sqrt{50}}{\sqrt{5}} \).
Solution: Apply the quotient rule for square roots:
\[
\frac{\sqrt{50}}{\sqrt{5}} = \sqrt{\frac{50}{5}} = \sqrt{10}
\] - Geometry Application:
A right triangle has legs of lengths \( 1 \) and \( \sqrt{5} \). Find the length of the hypotenuse.
Solution: Use the Pythagorean theorem:
\[
\text{Hypotenuse} = \sqrt{1^2 + (\sqrt{5})^2} = \sqrt{1 + 5} = \sqrt{6}
\] - Prime Factorization Method:
Express \( \sqrt{45} \) using prime factorization and simplify.
Solution: Prime factorize 45:
\[
45 = 3^2 \times 5
\]Therefore:
\[
\sqrt{45} = \sqrt{3^2 \times 5} = 3\sqrt{5}
\]
These practice problems will help you gain confidence in working with the square root of 5 in various contexts.
Đơn Giản Hóa Phân Số Dưới Dấu Căn - Mẹo Hợp Pháp Cho Toán Học
READ MORE:
Đơn Giản Hóa Căn Bậc Hai của 5