Topic 5 square root of 5: This article delves into the fascinating world of the 5 square root of 5, exploring its definition, calculation methods, and practical applications. Discover its mathematical significance, geometric interpretations, and relationship with Fibonacci numbers. Whether you're a student, educator, or math enthusiast, this comprehensive guide will enhance your understanding of this intriguing mathematical concept.
Table of Content
Understanding the Square Root of 5 (√5)
The square root of 5 (√5) is an interesting mathematical concept with various applications and properties. This article explores the value, calculation methods, and significance of √5.
Value of the Square Root of 5
The square root of 5 is an irrational number, which means it cannot be expressed as a simple fraction. Its approximate value to 50 decimal places is:
\[\sqrt{5} \approx 2.23606797749978969640917366873127623544061835961152\]
Geometric Significance
Geometrically, √5 represents the diagonal of a rectangle with side lengths of 1 and 2, which can be demonstrated using the Pythagorean theorem. It also appears in various trigonometric and algebraic contexts.
Calculation Methods
There are several ways to calculate the square root of 5:
- Using a calculator: Simply enter 5 and press the square root (√) button.
- Using a computer: Apply the SQRT function in Excel or Google Sheets:
=SQRT(5). - Long division method: An iterative manual calculation method that provides increasing accuracy.
Approximations and Representations
√5 can be approximated to various decimal places for practical uses:
- To the nearest tenth: 2.2
- To the nearest hundredth: 2.24
- To the nearest thousandth: 2.236
Relation to the Golden Ratio
The square root of 5 is closely related to the golden ratio (φ). The golden ratio can be expressed as:
\[\varphi = \frac{1 + \sqrt{5}}{2}\]
This relationship is significant in various fields including geometry, art, and architecture.
Simplification and Rationalization
The square root of 5 is already in its simplest form and cannot be simplified further. It remains an irrational number, meaning it cannot be precisely expressed as a fraction.
Practical Applications
Understanding and calculating the square root of 5 is useful in various mathematical problems, including solving quadratic equations, geometry problems, and in higher mathematics like calculus and number theory.
Examples
| Expression | Calculation | Result |
|---|---|---|
| \(5\sqrt{16} + 2\sqrt{25} - 2\sqrt{5}\) | \((5 \times 4) + (2 \times 5) - (2 \times 2.236)\) | 34.472 |
| \(\sqrt{5} - \sqrt{1}\) | \(2.236 - 1\) | 1.236 |
| \(20\sqrt{25} - 10\sqrt{9} - 5\sqrt{5}\) | \((20 \times 5) - (10 \times 3) - (5 \times 2.236)\) | 58.82 |
FAQs
- What is the square root of 5? The square root of 5 is approximately 2.23606.
- Is 5 a perfect square? No, 5 is not a perfect square because its square root is not a whole number.
- Is the square root of 5 a rational number? No, it is an irrational number.

READ MORE:
Introduction
The concept of the square root of 5, denoted as \( \sqrt{5} \), is a fascinating mathematical entity that appears frequently in various fields of study. It is an irrational number, meaning it cannot be expressed as a simple fraction, and its decimal representation is non-repeating and infinite. The value of \( \sqrt{5} \) is approximately 2.23607. This article will explore the properties, calculation methods, and practical applications of \( \sqrt{5} \), offering a comprehensive understanding of its significance.
- Definition and Explanation: Learn about the basic definition of \( \sqrt{5} \) and its characteristics.
- Calculation Methods: Discover various methods to calculate \( \sqrt{5} \), including manual and algorithmic approaches.
- Properties of the Square Root of 5: Explore the unique properties and attributes of \( \sqrt{5} \), such as its irrationality and geometric interpretations.
- Practical Applications: Understand how \( \sqrt{5} \) is used in different practical scenarios, including trigonometry and geometric constructions.
- Mathematical Significance: Delve into the historical and algebraic significance of \( \sqrt{5} \), and its relationship with famous number sequences like Fibonacci and Lucas numbers.
- Frequently Asked Questions: Get answers to common questions about \( \sqrt{5} \), its properties, and applications.
- Examples and Exercises: Practice with real-world examples and exercises to solidify your understanding of \( \sqrt{5} \).
Definition and Explanation
The square root of 5, denoted as \( \sqrt{5} \), is a mathematical constant that is the positive real number which, when multiplied by itself, equals 5. Formally, if \( x = \sqrt{5} \), then \( x^2 = 5 \).
\( \sqrt{5} \) is an irrational number, which means it cannot be expressed as a ratio of two integers. Its decimal representation is non-terminating and non-repeating:
\[
\sqrt{5} \approx 2.23606797749979...
\]
Understanding \( \sqrt{5} \) involves exploring its properties and various methods to approximate its value:
- Geometric Interpretation: The length of the diagonal of a rectangle with sides of lengths 1 and 2 is \( \sqrt{5} \). This follows from the Pythagorean theorem: \[ \text{Diagonal} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} \]
- Algebraic Significance: In algebra, \( \sqrt{5} \) often appears in the solutions of quadratic equations and in the study of quadratic fields.
- Approximation Methods:
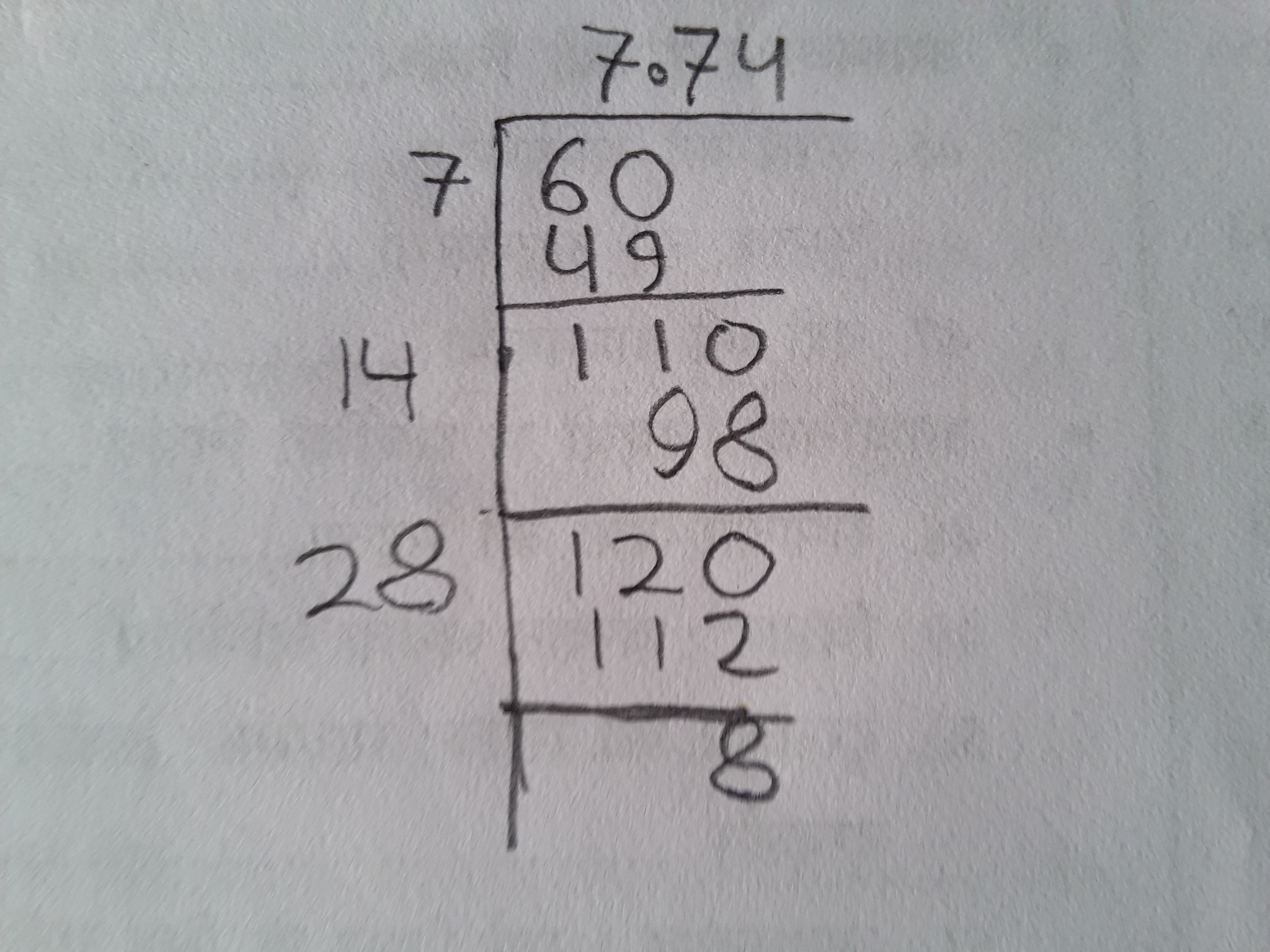
- Long Division Method: A manual algorithm to approximate square roots.
- Newton's Method: An iterative method that converges to the square root: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right) \]
The square root of 5 is also significant in various mathematical sequences. For instance, it plays a role in the derivation of the golden ratio, \( \phi \), which is given by the formula:
\[
\phi = \frac{1 + \sqrt{5}}{2}
\]
In summary, \( \sqrt{5} \) is a fundamental mathematical constant with wide-ranging applications and intriguing properties that extend into geometry, algebra, and number theory.
Properties of the Square Root of 5
The square root of 5, \( \sqrt{5} \), exhibits several interesting properties that make it a significant number in mathematics. These properties are explored in various mathematical contexts, from number theory to geometry.
- Irrationality:
\( \sqrt{5} \) is an irrational number, meaning it cannot be expressed as a fraction of two integers. Its decimal expansion is non-terminating and non-repeating:
\[
\sqrt{5} \approx 2.23606797749979...
\] - Geometric Interpretation:
In geometry, \( \sqrt{5} \) is often associated with the diagonal of a rectangle with sides 1 and 2. According to the Pythagorean theorem:
\[
\text{Diagonal} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]
This demonstrates how \( \sqrt{5} \) arises naturally in geometric constructions. - Relationship with Fibonacci and Lucas Numbers:
\( \sqrt{5} \) plays a crucial role in the closed-form expressions (Binet's formulas) for Fibonacci and Lucas numbers. For Fibonacci numbers \( F_n \):
\[
F_n = \frac{1}{\sqrt{5}} \left( \left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n \right)
\]
and for Lucas numbers \( L_n \):
\[
L_n = \left( \frac{1 + \sqrt{5}}{2} \right)^n + \left( \frac{1 - \sqrt{5}}{2} \right)^n
\] - Algebraic Significance:
\( \sqrt{5} \) is a root of the polynomial equation:
\[
x^2 - 5 = 0
\]
This polynomial has two roots, \( \sqrt{5} \) and \( -\sqrt{5} \), which are fundamental in the field of algebra. - Appearance in the Golden Ratio:
The golden ratio, \( \phi \), is closely related to \( \sqrt{5} \). It is defined as:
\[
\phi = \frac{1 + \sqrt{5}}{2}
\]
This ratio appears in various natural phenomena, art, and architecture, highlighting the importance of \( \sqrt{5} \).
These properties of \( \sqrt{5} \) showcase its significance in different areas of mathematics, making it a number of considerable interest and utility.
Mathematical Significance
The square root of 5, \( \sqrt{5} \), holds a special place in mathematics due to its unique properties and wide-ranging applications. Its significance can be explored through various mathematical contexts:
- Historical Context:
\( \sqrt{5} \) has been known since ancient times and has appeared in the works of many mathematicians. The Greeks, for example, explored irrational numbers and their geometric representations, recognizing the importance of \( \sqrt{5} \) in various constructions.
- Algebraic Significance:
In algebra, \( \sqrt{5} \) is a root of the quadratic equation:
\[
x^2 - 5 = 0
\]
Its presence in such fundamental equations underlines its importance in solving higher-order polynomials and in the study of quadratic fields. - Geometric Applications:
Geometry frequently uses \( \sqrt{5} \) to solve problems related to distances and shapes. For instance, the length of the diagonal in a rectangle with sides of length 1 and 2 is \( \sqrt{5} \), illustrating its role in the Pythagorean theorem:
\[
\text{Diagonal} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\] - Relationship with the Golden Ratio:
The golden ratio, \( \phi \), is closely linked to \( \sqrt{5} \). It is defined as:
\[
\phi = \frac{1 + \sqrt{5}}{2}
\]
This ratio is not only aesthetically significant but also appears in various natural patterns and phenomena, underscoring the importance of \( \sqrt{5} \). - Fibonacci and Lucas Numbers:
The expressions for Fibonacci and Lucas numbers involve \( \sqrt{5} \). The closed-form formula (Binet's formula) for the \( n \)-th Fibonacci number is:
\[
F_n = \frac{1}{\sqrt{5}} \left( \left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n \right)
\]
Similarly, Lucas numbers, which follow a related sequence, also incorporate \( \sqrt{5} \). - Continued Fractions:
\( \sqrt{5} \) can be represented as a continued fraction, which is a way to express numbers through an infinite sequence of nested fractions. The continued fraction for \( \sqrt{5} \) is:
\[
\sqrt{5} = 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \cdots}}}
\]
This representation is valuable in number theory and helps in understanding the properties of irrational numbers.
The mathematical significance of \( \sqrt{5} \) is vast and multi-faceted, influencing various areas of study and providing insight into the interconnectedness of mathematical concepts.

Frequently Asked Questions
- What is the Square Root of 5?
The square root of 5, denoted as \( \sqrt{5} \), is the positive real number that, when multiplied by itself, equals 5. Its approximate value is 2.23606797749979.
- Is the Square Root of 5 Rational or Irrational?
The square root of 5 is an irrational number. This means it cannot be expressed as a simple fraction of two integers. Its decimal representation is non-terminating and non-repeating.
- Can the Square Root of 5 Be Simplified?
The square root of 5 cannot be simplified further in terms of rational numbers or simple radicals. It is already in its simplest form.
- How is the Square Root of 5 Used in Geometry?
In geometry, \( \sqrt{5} \) often appears in calculations involving right triangles and rectangles. For example, the length of the diagonal of a rectangle with sides of length 1 and 2 is \( \sqrt{5} \).
- What is the Relationship Between the Square Root of 5 and the Golden Ratio?
The golden ratio, \( \phi \), is closely related to \( \sqrt{5} \). It is defined as:
\[
\phi = \frac{1 + \sqrt{5}}{2}
\]
This ratio appears in many natural patterns, artworks, and architectural designs. - How Do You Calculate the Square Root of 5 Using Iterative Methods?
One common iterative method to calculate \( \sqrt{5} \) is Newton's method (Heron's method). Start with an initial guess \( x_0 \) and use the formula:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right)
\]
Repeat the iteration until the desired level of accuracy is achieved. - Why is the Square Root of 5 Important in Number Theory?
In number theory, \( \sqrt{5} \) is significant because it appears in the expressions for Fibonacci and Lucas numbers, as well as in the study of quadratic fields and Diophantine equations.
- What are Some Practical Applications of the Square Root of 5?
Practical applications of \( \sqrt{5} \) include its use in trigonometric identities, solving quadratic equations, and in various scientific and engineering calculations where precise measurements are required.
Examples and Exercises
Understanding the square root of 5, \( \sqrt{5} \), can be enhanced through practical examples and exercises. Below are some problems to help solidify your knowledge:
Examples
- Example 1: Simplifying Expressions
Simplify the expression:
\[
3\sqrt{5} + 2\sqrt{5}
\]
Solution:
Combine like terms:
\[
3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}
\] - Example 2: Solving Quadratic Equations
Solve the quadratic equation:
\[
x^2 - 5 = 0
\]
Solution:
Add 5 to both sides:
\[
x^2 = 5
\]
Take the square root of both sides:
\[
x = \pm \sqrt{5}
\] - Example 3: Diagonal of a Rectangle
Find the diagonal of a rectangle with sides 1 and 2 units.
Solution:
Using the Pythagorean theorem:
\[
\text{Diagonal} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]
So, the diagonal is \( \sqrt{5} \) units long.
Exercises
- Exercise 1: Simplify
Simplify the expression:
\[
4\sqrt{5} - \sqrt{5}
\]
Hint: Combine like terms. - Exercise 2: Solve for x
Solve the quadratic equation:
\[
x^2 = 5
\]
Hint: Take the square root of both sides. - Exercise 3: Perimeter of a Rectangle
Find the perimeter of a rectangle with sides of length 1 and \( \sqrt{5} \) units.
Hint: Use the formula for the perimeter of a rectangle: \( P = 2(l + w) \). - Exercise 4: Rationalizing the Denominator
Rationalize the denominator of:
\[
\frac{1}{\sqrt{5}}
\]
Hint: Multiply the numerator and denominator by \( \sqrt{5} \). - Exercise 5: Continued Fraction
Express \( \sqrt{5} \) as a continued fraction.
Hint: Start with the approximate value and find the repeating pattern.
These examples and exercises provide practical applications and challenges that help deepen the understanding of the square root of 5, enhancing both algebraic and geometric skills.
Conclusion
The square root of 5, denoted as \( \sqrt{5} \), is an irrational number with a decimal approximation of approximately 2.2360679775. It has various mathematical properties and applications across different fields.
- Mathematically, \( \sqrt{5} \) plays a significant role in geometry, particularly in root rectangles and geometric constructions.
- It is closely related to the Fibonacci sequence and Lucas numbers, appearing in their formulas and providing insights into their growth patterns.
- In trigonometry, \( \sqrt{5} \) contributes to fundamental formulas and identities, enriching the understanding of geometric relationships.
- Historically, \( \sqrt{5} \) has been a subject of interest since ancient times, influencing mathematical developments and theories.
- Despite its simplicity in representation, \( \sqrt{5} \) remains an intriguing and valuable concept in both theoretical and applied mathematics.
Exploring \( \sqrt{5} \) reveals its pervasive presence and enduring relevance in mathematical theory and practice, continuing to inspire further research and applications.
Xem video để hiểu rõ hơn về bình phương của số 5 và các phương pháp đơn giản hóa liên quan.
Video Titled "Bình Phương Của 5 Được Đơn Giản Hóa"
READ MORE:
Xem video để học cách tìm căn bậc hai của số 5 bằng phương pháp chia hết dài.
Video Titled "Cách Tìm Căn Bậc Hai của 5 bằng Phương Pháp Chia Hết Dài / Căn bậc hai của 5 / Tìm Căn Bậc Hai của 5"