Topic simplify square root of 25: Understanding how to simplify the square root of 25 is essential for mastering basic math concepts. In this article, we'll walk you through easy and clear steps to simplify square roots, starting with 25. Whether you're a student or just looking to refresh your math skills, this guide will make the process simple and straightforward.
Table of Content
- Results for Simplify Square Root of 25
- Introduction to Square Roots
- Definition of Square Roots
- Basic Principles of Simplifying Square Roots
- Step-by-Step Guide to Simplifying Square Root of 25
- Understanding Perfect Squares
- Examples of Simplifying Other Perfect Square Roots
- Common Mistakes to Avoid
- Practical Applications of Square Roots
- Visual Representation of Square Roots
- Advanced Topics in Square Roots
- FAQs About Square Roots
- Conclusion
- YOUTUBE: Học cách đơn giản hóa căn bậc hai của số 25 trong bài hướng dẫn này. Xem video để hiểu rõ hơn về phép tính này và cách áp dụng nó.
Results for Simplify Square Root of 25
The square root of 25 simplifies to 5.
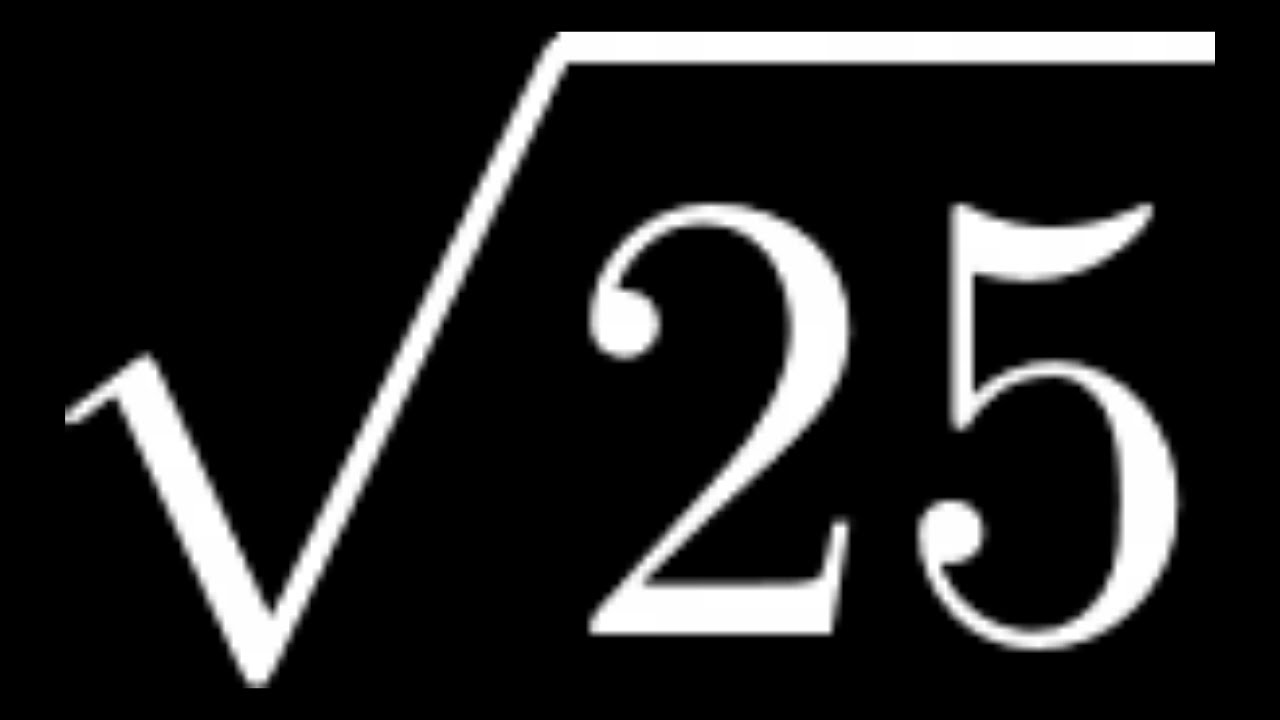
READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics that are essential for understanding more advanced topics. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\).
Square roots are represented by the radical symbol \( \sqrt{} \). The expression \( \sqrt{25} \) reads as "the square root of 25". Square roots can be both positive and negative because both \( 5 \times 5 \) and \( -5 \times -5 \) equal 25. However, in most cases, the positive root is considered the principal square root.
Here is a step-by-step breakdown to understand square roots:
- Identify the number you want to find the square root of.
- Determine if the number is a perfect square (a number that has an integer as its square root).
- Use the radical symbol to represent the square root.
- Simplify the square root if possible.
For instance, with the number 25:
- Identify the number: 25
- Determine if it's a perfect square: Yes, because \(5 \times 5 = 25\)
- Use the radical symbol: \( \sqrt{25} \)
- Simplify: \( \sqrt{25} = 5 \)
Understanding square roots and how to simplify them is a crucial skill in mathematics, providing the foundation for more complex operations and problem-solving techniques.
Definition of Square Roots
A square root of a number is a value that, when multiplied by itself, results in the original number. Mathematically, if \( x \) is the square root of \( y \), then \( x^2 = y \). This concept is fundamental in various areas of mathematics and is often represented using the radical symbol \( \sqrt{} \).
For example, the square root of 25 is denoted as \( \sqrt{25} \). Since \( 5 \times 5 = 25 \), we can say \( \sqrt{25} = 5 \). It's important to note that every positive number has two square roots: one positive and one negative. Therefore, the square roots of 25 are \( +5 \) and \( -5 \), as both satisfy the equation \( x^2 = 25 \).
Here is a detailed breakdown of the definition of square roots:
- Radical Symbol: The square root is represented by the radical symbol \( \sqrt{} \). For example, \( \sqrt{16} \) represents the square root of 16.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers. For instance, \( \sqrt{16} = 4 \) and \( \sqrt{25} = 5 \).
- Principal Square Root: The non-negative square root is known as the principal square root. For example, the principal square root of 25 is 5.
- Negative Square Root: Every positive number also has a negative square root. Therefore, the negative square root of 25 is -5.
To summarize, the square root function helps us determine which number, when squared, will give us the original value. This function is essential in solving equations and understanding various mathematical concepts.
Basic Principles of Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest form. This process can make calculations easier and results more understandable. Here are the basic principles to follow when simplifying square roots:
-
Identify Perfect Squares:
Determine if the number under the square root is a perfect square. Perfect squares are numbers like 1, 4, 9, 16, and 25, which have whole numbers as their square roots.
-
Factorize the Number:
Break down the number under the square root into its prime factors. For example, to simplify \( \sqrt{72} \), factorize 72 into prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
-
Pair the Factors:
Group the prime factors into pairs. Each pair of identical factors can be taken out of the square root as a single factor. Using the example above, \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
-
Simplify the Expression:
Combine the factors taken out of the square root with the remaining factors inside the square root. Ensure the expression is in its simplest form.
Let's apply these principles to the square root of 25:
- Identify the number: 25
- Determine if it's a perfect square: Yes, because \( 25 = 5 \times 5 \)
- Factorize the number: \( 25 = 5 \times 5 \)
- Pair the factors: \( \sqrt{25} = \sqrt{5 \times 5} \)
- Simplify the expression: \( \sqrt{25} = 5 \)
By following these basic principles, you can simplify any square root. The key is to identify perfect squares and factorize the number properly, making calculations more manageable and results clearer.
Step-by-Step Guide to Simplifying Square Root of 25
Simplifying the square root of 25 is a straightforward process since 25 is a perfect square. Here is a detailed step-by-step guide to simplify \( \sqrt{25} \):
-
Identify the Number:
The number we need to simplify is 25.
-
Determine if it is a Perfect Square:
Check if 25 is a perfect square. A perfect square is a number that has an integer as its square root. Since \( 5 \times 5 = 25 \), we know that 25 is a perfect square.
-
Express as a Product of Two Identical Factors:
Write 25 as the product of two identical factors: \( 25 = 5 \times 5 \).
-
Apply the Square Root Operation:
Take the square root of both sides of the equation: \( \sqrt{25} = \sqrt{5 \times 5} \).
-
Simplify the Square Root:
Since the square root of a product of two identical factors is simply the factor itself, we get \( \sqrt{5 \times 5} = 5 \).
Thus, \( \sqrt{25} = 5 \). This process shows that simplifying the square root of a perfect square like 25 results in an integer.
To summarize:
- Identify the number: 25
- Recognize it as a perfect square: \( 5 \times 5 = 25 \)
- Write it under the square root: \( \sqrt{25} \)
- Simplify to get the result: 5
By following these steps, you can simplify any perfect square easily. Understanding this method is essential for tackling more complex square root problems in mathematics.

Understanding Perfect Squares
Perfect squares are fundamental concepts in mathematics, representing numbers that can be expressed as the product of an integer with itself. Understanding perfect squares is essential for simplifying square roots and solving various mathematical problems. Here's a detailed explanation:
A perfect square is a number that can be written as \( n^2 \), where \( n \) is an integer. For example, the numbers 1, 4, 9, 16, and 25 are perfect squares because they can be written as:
- \( 1 = 1 \times 1 = 1^2 \)
- \( 4 = 2 \times 2 = 2^2 \)
- \( 9 = 3 \times 3 = 3^2 \)
- \( 16 = 4 \times 4 = 4^2 \)
- \( 25 = 5 \times 5 = 5^2 \)
Perfect squares have several important properties:
-
Non-negative Results:
Perfect squares are always non-negative because the product of two identical integers is never negative. For example, \( (-3) \times (-3) = 9 \).
-
Integer Square Roots:
The square root of a perfect square is always an integer. For instance, \( \sqrt{25} = 5 \) because \( 25 = 5^2 \).
-
Even and Odd Properties:
The square of an even number is even, and the square of an odd number is odd. For example, \( 4^2 = 16 \) (even), and \( 5^2 = 25 \) (odd).
Identifying perfect squares is crucial when simplifying square roots. When you recognize a number as a perfect square, you can immediately determine its square root. For example, knowing that 36 is a perfect square (since \( 6 \times 6 = 36 \)) allows you to simplify \( \sqrt{36} \) to 6.
Let's apply this understanding to simplify the square root of 25:
- Identify that 25 is a perfect square because \( 5 \times 5 = 25 \).
- Express it as \( 25 = 5^2 \).
- Simplify the square root: \( \sqrt{25} = 5 \).
Recognizing perfect squares and their properties simplifies many mathematical processes and is a foundational skill in algebra and beyond.
Examples of Simplifying Other Perfect Square Roots
Understanding how to simplify the square root of 25 can be extended to other perfect square roots. Below are examples that illustrate the process of simplifying different perfect square roots step by step.
Example 1: Simplifying \( \sqrt{36} \)
-
Identify the Number:
The number we need to simplify is 36.
-
Determine if it is a Perfect Square:
Check if 36 is a perfect square. Since \( 6 \times 6 = 36 \), we know that 36 is a perfect square.
-
Express as a Product of Two Identical Factors:
Write 36 as the product of two identical factors: \( 36 = 6 \times 6 \).
-
Apply the Square Root Operation:
Take the square root of both sides of the equation: \( \sqrt{36} = \sqrt{6 \times 6} \).
-
Simplify the Square Root:
Since the square root of a product of two identical factors is simply the factor itself, we get \( \sqrt{6 \times 6} = 6 \).
Example 2: Simplifying \( \sqrt{49} \)
-
Identify the Number:
The number we need to simplify is 49.
-
Determine if it is a Perfect Square:
Check if 49 is a perfect square. Since \( 7 \times 7 = 49 \), we know that 49 is a perfect square.
-
Express as a Product of Two Identical Factors:
Write 49 as the product of two identical factors: \( 49 = 7 \times 7 \).
-
Apply the Square Root Operation:
Take the square root of both sides of the equation: \( \sqrt{49} = \sqrt{7 \times 7} \).
-
Simplify the Square Root:
Since the square root of a product of two identical factors is simply the factor itself, we get \( \sqrt{7 \times 7} = 7 \).
Example 3: Simplifying \( \sqrt{81} \)
-
Identify the Number:
The number we need to simplify is 81.
-
Determine if it is a Perfect Square:
Check if 81 is a perfect square. Since \( 9 \times 9 = 81 \), we know that 81 is a perfect square.
-
Express as a Product of Two Identical Factors:
Write 81 as the product of two identical factors: \( 81 = 9 \times 9 \).
-
Apply the Square Root Operation:
Take the square root of both sides of the equation: \( \sqrt{81} = \sqrt{9 \times 9} \).
-
Simplify the Square Root:
Since the square root of a product of two identical factors is simply the factor itself, we get \( \sqrt{9 \times 9} = 9 \).
By following these steps, you can simplify any perfect square root, making it easier to handle various mathematical problems.
Common Mistakes to Avoid
When simplifying square roots, particularly those of perfect squares like 25, it's easy to make mistakes. Here are some common errors and how to avoid them:
-
Forgetting to Recognize Perfect Squares:
A common mistake is failing to identify a number as a perfect square. Always check if the number under the square root is a perfect square. For example, recognize that 25 is \( 5 \times 5 \) before simplifying \( \sqrt{25} \) to 5.
-
Incorrect Factorization:
Ensure accurate factorization of the number. For instance, factorizing 36 correctly as \( 6 \times 6 \) instead of mistakenly factorizing it as \( 4 \times 9 \), which would complicate simplification.
-
Not Simplifying Completely:
After factorizing, ensure you simplify the square root completely. For example, \( \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \), not just leaving it as \( \sqrt{36 \times 2} \).
-
Confusing Principal and Negative Roots:
Remember that while a number can have both positive and negative square roots, the principal square root (denoted by \( \sqrt{} \)) is always non-negative. For instance, \( \sqrt{25} = 5 \), not -5.
-
Improper Use of the Radical Symbol:
Make sure the radical symbol \( \sqrt{} \) is used correctly and not omitted. Miswriting or skipping this symbol can lead to confusion and incorrect results.
-
Arithmetic Errors:
Basic arithmetic mistakes can easily occur. Double-check your multiplication and factorization. For example, ensure \( 49 = 7 \times 7 \) before concluding \( \sqrt{49} = 7 \).
By being aware of these common mistakes and taking care to avoid them, you can simplify square roots more accurately and efficiently.
Practical Applications of Square Roots
Square roots are not just theoretical concepts; they have numerous practical applications in various fields. Understanding and using square roots can help solve real-world problems effectively. Here are some key practical applications:
1. Geometry and Trigonometry
Square roots are essential in geometry and trigonometry for calculating distances, areas, and angles. For example:
-
Distance Formula:
In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
-
Pythagorean Theorem:
In a right-angled triangle, the length of the hypotenuse \( c \) is found using \( c = \sqrt{a^2 + b^2} \), where \( a \) and \( b \) are the lengths of the other two sides.
2. Physics and Engineering
Square roots are frequently used in physics and engineering calculations, such as:
-
Wave Speeds:
The speed of a wave on a string is determined by \( v = \sqrt{\frac{T}{\mu}} \), where \( T \) is the tension and \( \mu \) is the mass per unit length.
-
Electrical Engineering:
Calculating root mean square (RMS) values for alternating current (AC) signals involves the square root of the mean of the squares of the instantaneous values.
3. Finance and Economics
Square roots are used in finance and economics for various calculations, including:
-
Volatility:
To calculate the standard deviation or volatility of stock prices, square roots are used in the formula \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \), where \( x_i \) represents individual stock returns, \( \mu \) is the mean return, and \( N \) is the number of observations.
-
Compound Interest:
The formula for compound interest can involve square roots when solving for the interest rate or time period: \( A = P \left(1 + \frac{r}{n}\right)^{nt} \).
4. Medicine and Biology
In medicine and biology, square roots are used in statistical analyses and measurements, such as:
-
Body Mass Index (BMI):
The BMI formula \( \text{BMI} = \frac{\text{weight (kg)}}{\text{height (m)}^2} \) involves the square of height. To solve for height, the square root is used.
-
Pharmacokinetics:
Square roots are used to model drug concentration in the bloodstream over time, often involving half-life equations.
These examples illustrate the versatility and importance of square roots in various practical applications, highlighting their relevance beyond pure mathematics.

Visual Representation of Square Roots
Visualizing square roots can help deepen our understanding of these mathematical concepts. Here's a step-by-step visual guide to simplifying the square root of 25:
- Start with the number 25.
- Recognize that 25 is a perfect square because it can be expressed as \(5 \times 5\).
- To simplify \( \sqrt{25} \), visualize a square with sides of length 5 units.
- Imagine this square divided into smaller squares, each with an area of 1 square unit.
- Count the number of these smaller squares that form the larger square. For \( \sqrt{25} \), there are exactly 5 such smaller squares along each side.
- Hence, \( \sqrt{25} = 5 \).
This visual representation demonstrates that \( \sqrt{25} \) equals the side length of a square with an area of 25 square units, divided into smaller 1 square unit sections. This method can be applied similarly to other perfect square roots for better comprehension.
Advanced Topics in Square Roots
Advanced topics in square roots delve into more complex aspects beyond basic simplification. Here are key concepts:
- Rationalizing Denominators: Involves removing square roots from the denominator of fractions.
- Imaginary Numbers: Introduction to square roots of negative numbers, denoted as \( \sqrt{-1} = i \).
- Non-Perfect Square Roots: Techniques for approximating square roots of numbers that are not perfect squares.
- Radical Equations: Solving equations involving square roots, such as \( \sqrt{x+2} = 4 \).
- Graphical Representations: Visualizing square roots on coordinate axes, understanding the graphs of \( y = \sqrt{x} \) and \( y = \sqrt{x - h} + k \).
- Applications in Geometry and Physics: Utilizing square roots in fields like calculating distances, areas, and volumes.
FAQs About Square Roots
- What is a square root?
A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For example, \( \sqrt{25} = 5 \) because \( 5^2 = 25 \).
- How do you simplify the square root of 25?
The square root of 25 simplifies to 5 because 25 is a perfect square (5 times 5).
- Can square roots be negative?
No, the square root of a non-negative number is always non-negative. For instance, \( \sqrt{25} = 5 \) and \( \sqrt{0} = 0 \).
- What is the difference between \( \sqrt{x} \) and \( x^{1/2} \)?
They represent the same mathematical operation. \( \sqrt{x} \) is the principal square root (non-negative), while \( x^{1/2} \) can include both positive and negative roots.
- How are square roots used in real life?
Square roots are used in various fields such as engineering, physics, and finance for calculations involving areas, volumes, distances, and statistical analysis.
Conclusion
Understanding how to simplify the square root of 25 is foundational to mastering the concept of square roots. Here’s a recap:
- We started by defining what a square root is and its basic properties.
- We explored the specific case of \( \sqrt{25} \) and saw that it simplifies to 5.
- Visual representations helped us visualize the square root as the side length of a square with an area of 25 square units.
- We discussed common mistakes to avoid and the importance of recognizing perfect squares.
- Advanced topics such as rationalizing denominators and solving radical equations expanded our understanding.
- Lastly, we explored practical applications of square roots in various fields.
By mastering these concepts, you’re well-equipped to apply square roots in both academic and real-world scenarios. Remember, practice is key to enhancing your proficiency in mathematical operations involving square roots.

Học cách đơn giản hóa căn bậc hai của số 25 trong bài hướng dẫn này. Xem video để hiểu rõ hơn về phép tính này và cách áp dụng nó.
Cách đơn giản hóa căn bậc hai của 25 | Video Hướng dẫn
READ MORE:
Học cách đơn giản hóa căn bậc hai của số 25 trong bài hướng dẫn toán học này. Xem video để hiểu rõ hơn về phép tính này và cách áp dụng nó.
Cách đơn giản hóa căn bậc hai của 25 | Hướng dẫn Toán học












