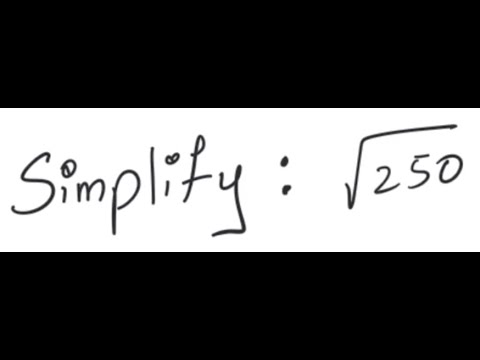Topic 50 square root simplified: Understanding how to simplify square roots is essential for mastering various mathematical concepts. In this guide, we will focus on simplifying the square root of 50. With step-by-step instructions and practical examples, you'll find the process straightforward and manageable. Let's explore the methods and techniques to simplify √50 efficiently.
Table of Content
- Understanding the Simplification of the Square Root of 50
- Introduction to Square Roots
- Basic Concept of Simplifying Square Roots
- Prime Factorization Method for Simplification
- Step-by-Step Process to Simplify \(\sqrt{50}\)
- Alternative Methods for Simplifying Square Roots
- Visual Representation of \(\sqrt{50}\) Simplification
- Applications of Simplified Square Roots in Mathematics
- Common Mistakes to Avoid During Simplification
- Practice Problems and Solutions
- Conclusion and Summary
- YOUTUBE: Tìm hiểu cách đơn giản hóa căn bậc hai của 50 một cách dễ dàng và chính xác. Video hướng dẫn chi tiết để giúp bạn hiểu rõ hơn về quá trình đơn giản hóa căn bậc hai.
Understanding the Simplification of the Square Root of 50
The square root of 50 can be simplified by finding its prime factorization and then simplifying the radicals. This process helps in reducing the square root to its simplest form.
Step-by-Step Simplification
- Prime factorize the number 50:
- 50 = 2 × 5 × 5
- Express the square root using the prime factors:
- \(\sqrt{50} = \sqrt{2 \times 5 \times 5}\)
- Group the pairs of prime factors:
- \(\sqrt{50} = \sqrt{5^2 \times 2}\)
- Simplify the square root:
- \(\sqrt{50} = 5 \sqrt{2}\)
Visual Representation
To better understand the simplification process, refer to the visual representation below:
Summary
The simplified form of \(\sqrt{50}\) is \(5\sqrt{2}\). This form is more concise and easier to work with in various mathematical contexts.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\). Square roots are denoted by the radical symbol (√).
When simplifying square roots, the goal is to express the square root in its simplest form. This often involves breaking down the number under the radical into its prime factors and then simplifying accordingly.
- Identify the number whose square root you need to simplify.
- Perform prime factorization of the number.
- Group the prime factors into pairs.
- Move each pair out of the radical as a single number.
- Multiply the numbers outside the radical to get the simplified form.
Let's take a closer look at the process of simplifying the square root of 50 in the following sections.
Basic Concept of Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. This process makes complex calculations easier and more understandable. The simplification process relies on identifying and extracting perfect squares from under the radical sign.
Here are the steps to simplify a square root:
- Identify the number you need to simplify the square root of. For example, let's simplify \(\sqrt{50}\).
- Perform prime factorization on the number. Prime factorization of 50 is \(50 = 2 \times 5 \times 5\).
- Rewrite the number under the square root as a product of its prime factors: \(\sqrt{50} = \sqrt{2 \times 5^2}\).
- Identify and separate the perfect square from the product: \(\sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}\).
- Simplify the square root of the perfect square: \(\sqrt{5^2} = 5\).
- Combine the simplified parts: \(\sqrt{50} = 5\sqrt{2}\).
By following these steps, you can simplify the square root of any number. Simplifying square roots helps in making further mathematical operations easier and more efficient.
Prime Factorization Method for Simplification
The prime factorization method is an effective way to simplify square roots by breaking down a number into its prime factors. This method makes it easier to identify perfect squares that can be simplified. Here’s a step-by-step guide to using the prime factorization method to simplify the square root of 50:
- Find the Prime Factors:
First, determine the prime factors of the number under the square root. For 50, the prime factors are:
- 50 ÷ 2 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
So, the prime factorization of 50 is \(2 \times 5 \times 5\) or \(2 \times 5^2\).
- Express Under the Radical:
Rewrite the square root using the prime factors: \(\sqrt{50} = \sqrt{2 \times 5^2}\).
- Separate Perfect Squares:
Identify and separate the perfect squares from the product: \(\sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}\).
- Simplify the Perfect Squares:
Simplify the square root of the perfect square: \(\sqrt{5^2} = 5\).
- Combine the Results:
Combine the simplified parts to get the simplified form: \(\sqrt{50} = 5\sqrt{2}\).
By following these steps, you can simplify square roots efficiently using the prime factorization method. This approach helps in breaking down complex numbers into manageable parts, making the simplification process straightforward.
Step-by-Step Process to Simplify \(\sqrt{50}\)
Simplifying \(\sqrt{50}\) involves breaking down the number into its prime factors and simplifying accordingly. Here’s a detailed step-by-step process:
- Prime Factorization:
Start by finding the prime factors of 50:
- 50 can be divided by 2: \(50 \div 2 = 25\)
- 25 can be divided by 5: \(25 \div 5 = 5\)
- 5 can be divided by 5: \(5 \div 5 = 1\)
So, the prime factors of 50 are \(2 \times 5 \times 5\) or \(2 \times 5^2\).
- Rewrite the Radical Expression:
Express the square root using these prime factors:
\(\sqrt{50} = \sqrt{2 \times 5^2}\)
- Separate the Perfect Squares:
Identify and separate the perfect squares within the radical:
\(\sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}\)
- Simplify the Perfect Squares:
Simplify the square root of the perfect square:
\(\sqrt{5^2} = 5\)
- Combine the Simplified Terms:
Combine the simplified terms to get the final simplified form:
\(\sqrt{50} = 5\sqrt{2}\)
By following these steps, you can simplify \(\sqrt{50}\) to its simplest form, \(5\sqrt{2}\), making it easier to work with in various mathematical contexts.

Alternative Methods for Simplifying Square Roots
While the prime factorization method is a common way to simplify square roots, there are other methods that can also be used. Here are a few alternative approaches:
Method 1: Estimation and Refinement
- Estimate the Square Root:
Find two perfect squares between which the number lies. For example, 50 lies between 49 (\(7^2\)) and 64 (\(8^2\)). So, \(\sqrt{50}\) is between 7 and 8.
- Refine the Estimate:
Use average approximation for a closer estimate. If \(\sqrt{50}\) is close to 7.1, check: \(7.1^2 = 50.41\). Since 50.41 is very close to 50, 7.1 is a good estimate.
Method 2: Repeated Subtraction of Odd Numbers
- Understand the Concept:
The square root of a number can be found by repeatedly subtracting odd numbers from the original number until you reach zero.
- Apply the Method:
- 50 - 1 = 49
- 49 - 3 = 46
- 46 - 5 = 41
- 41 - 7 = 34
- 34 - 9 = 25
- 25 - 11 = 14
- 14 - 13 = 1
Count the number of subtractions: 7 subtractions, so \(\sqrt{50}\) is approximately 7.
Method 3: Using a Calculator for Decimal Form
- Use a Scientific Calculator:
Enter the number 50 and press the square root button to get the decimal form of the square root. For example, \(\sqrt{50} \approx 7.071\).
- Express in Simplified Radical Form:
If needed, convert the decimal back to simplified radical form using known values. Here, \(7.071 \approx 5\sqrt{2}\).
These alternative methods provide different ways to simplify or approximate square roots, offering flexibility depending on the context and available tools.
Visual Representation of \(\sqrt{50}\) Simplification
Visualizing the simplification of \(\sqrt{50}\) can make the process clearer and more intuitive. Here, we use a step-by-step visual approach to break down the simplification.
Step 1: Prime Factorization
We start with the prime factorization of 50:
- 50 ÷ 2 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
This gives us \(50 = 2 \times 5^2\).
Step 2: Rewrite Under the Radical
Express the square root using prime factors:
\(\sqrt{50} = \sqrt{2 \times 5^2}\)
Step 3: Separate the Perfect Squares
Identify and separate the perfect square from the product:
\(\sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}\)
Step 4: Simplify the Perfect Squares
Simplify the square root of the perfect square:
\(\sqrt{5^2} = 5\)
Step 5: Combine the Simplified Terms
Combine the simplified parts to get the final simplified form:
\(\sqrt{50} = 5\sqrt{2}\)
Visual Aid:
| Original Expression | \(\sqrt{50}\) |
| Prime Factorization | \(2 \times 5 \times 5\) |
| Rewrite with Radicals | \(\sqrt{2 \times 5^2}\) |
| Separate Perfect Squares | \(\sqrt{2} \times \sqrt{5^2}\) |
| Simplify | \(5\sqrt{2}\) |
By breaking down each step visually, the process of simplifying \(\sqrt{50}\) becomes easier to understand and follow.
Applications of Simplified Square Roots in Mathematics
Simplified square roots have a wide range of applications in various areas of mathematics. Simplifying square roots makes calculations easier and helps in solving complex mathematical problems more efficiently. Here are some key applications:
1. Solving Quadratic Equations
Quadratic equations often involve square roots. Simplifying these roots can make it easier to find solutions. For example, solving \(x^2 - 50 = 0\) involves finding \(x = \pm \sqrt{50} = \pm 5\sqrt{2}\).
2. Geometry and Trigonometry
Simplified square roots are used in geometry to find distances, areas, and other measurements. For example, the diagonal of a square with side length 5 is \(\sqrt{50} = 5\sqrt{2}\).
3. Algebraic Simplification
Simplifying square roots helps in algebraic expressions and equations. For example, combining like terms involving square roots is easier with simplified roots: \(3\sqrt{50} + 2\sqrt{50} = 3(5\sqrt{2}) + 2(5\sqrt{2}) = 5\sqrt{2}(3 + 2) = 25\sqrt{2}\).
4. Calculus
In calculus, simplified square roots are often used in integration and differentiation. For instance, integrating functions involving \(\sqrt{x}\) becomes more manageable when expressed in simplified form.
5. Real-World Applications
Many real-world problems, such as physics and engineering, involve square roots. Simplified square roots make it easier to handle these problems. For example, calculating the hypotenuse in the Pythagorean theorem involves simplifying square roots: \(c = \sqrt{a^2 + b^2}\).
6. Simplifying Radical Expressions
Mathematical problems often involve simplifying expressions with radicals. For example, simplifying the expression \(\sqrt{200} + \sqrt{50}\) involves converting to simplified forms: \(10\sqrt{2} + 5\sqrt{2} = 15\sqrt{2}\).
Overall, the ability to simplify square roots is an essential skill in mathematics, making complex problems more manageable and solutions more elegant.
Common Mistakes to Avoid During Simplification
Simplifying square roots can sometimes lead to mistakes if certain steps are not followed correctly. Here are some common mistakes to avoid and tips to ensure accurate simplification:
- Ignoring Prime Factorization:
One common mistake is not performing prime factorization correctly. Ensure that you break down the number into its prime factors accurately. For example, 50 should be factored as \(2 \times 5^2\).
- Forgetting to Simplify All Parts:
Another mistake is not simplifying all parts of the expression. For example, in \(\sqrt{2 \times 5^2}\), ensure both parts are simplified to get \(5\sqrt{2}\).
- Incorrectly Identifying Perfect Squares:
Sometimes, students incorrectly identify or ignore perfect squares. Ensure that you correctly identify and separate perfect squares from the rest of the factors.
- Combining Non-Like Terms:
Ensure that you only combine like terms. For example, \(\sqrt{50} + \sqrt{18}\) should not be combined directly. Instead, simplify each term first: \(5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}\).
- Not Simplifying Radicals Completely:
Always check if the radical can be simplified further. For example, \(\sqrt{72}\) can be simplified to \(6\sqrt{2}\), not just left as \(\sqrt{72}\).
- Arithmetic Errors:
Be careful with arithmetic calculations during the simplification process. Small errors in multiplication or division can lead to incorrect simplification.
By being aware of these common mistakes and carefully following each step, you can simplify square roots accurately and efficiently.

Practice Problems and Solutions
Practicing simplification of square roots is essential for mastering this concept. Here are some practice problems along with detailed solutions to help you understand the process step by step.
Problem 1: Simplify \(\sqrt{75}\)
- Find the Prime Factors:
75 can be factored as \(75 = 3 \times 5 \times 5\) or \(3 \times 5^2\).
- Rewrite the Radical Expression:
\(\sqrt{75} = \sqrt{3 \times 5^2}\)
- Separate the Perfect Squares:
\(\sqrt{3 \times 5^2} = \sqrt{3} \times \sqrt{5^2}\)
- Simplify the Perfect Squares:
\(\sqrt{5^2} = 5\)
- Combine the Simplified Terms:
\(\sqrt{75} = 5\sqrt{3}\)
Problem 2: Simplify \(\sqrt{32}\)
- Find the Prime Factors:
32 can be factored as \(32 = 2 \times 2 \times 2 \times 2 \times 2\) or \(2^5\).
- Rewrite the Radical Expression:
\(\sqrt{32} = \sqrt{2^5}\)
- Separate the Perfect Squares:
\(\sqrt{2^5} = \sqrt{2^4 \times 2} = \sqrt{2^4} \times \sqrt{2}\)
- Simplify the Perfect Squares:
\(\sqrt{2^4} = 2^2 = 4\)
- Combine the Simplified Terms:
\(\sqrt{32} = 4\sqrt{2}\)
Problem 3: Simplify \(\sqrt{200}\)
- Find the Prime Factors:
200 can be factored as \(200 = 2 \times 2 \times 2 \times 5 \times 5\) or \(2^3 \times 5^2\).
- Rewrite the Radical Expression:
\(\sqrt{200} = \sqrt{2^3 \times 5^2}\)
- Separate the Perfect Squares:
\(\sqrt{2^3 \times 5^2} = \sqrt{2^2 \times 2 \times 5^2} = \sqrt{2^2} \times \sqrt{5^2} \times \sqrt{2}\)
- Simplify the Perfect Squares:
\(\sqrt{2^2} = 2\) and \(\sqrt{5^2} = 5\)
- Combine the Simplified Terms:
\(\sqrt{200} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}\)
By practicing these problems and following the steps carefully, you can improve your skills in simplifying square roots.
Conclusion and Summary
Simplifying square roots is a fundamental skill in mathematics that can make complex calculations more manageable and intuitive. The process of simplifying \(\sqrt{50}\) exemplifies the method of breaking down a square root into its prime factors and simplifying it to its most basic form.
Here's a brief summary of the key points covered in this guide:
- Introduction to Square Roots: Understanding the concept of square roots and their significance in mathematics.
- Basic Concept of Simplifying Square Roots: Learning why and how square roots can be simplified.
- Prime Factorization Method for Simplification: Utilizing the prime factorization technique to simplify square roots.
- Step-by-Step Process to Simplify \(\sqrt{50}\): A detailed walkthrough of simplifying \(\sqrt{50}\) using prime factorization, resulting in \(\sqrt{50} = 5\sqrt{2}\).
- Alternative Methods for Simplifying Square Roots: Exploring other approaches to simplifying square roots, such as using properties of exponents.
- Visual Representation of \(\sqrt{50}\) Simplification: Illustrating the simplification process with diagrams and visual aids for better comprehension.
- Applications of Simplified Square Roots in Mathematics: Discussing the practical uses of simplified square roots in various mathematical contexts.
- Common Mistakes to Avoid During Simplification: Highlighting frequent errors and how to avoid them when simplifying square roots.
- Practice Problems and Solutions: Providing exercises and detailed solutions to reinforce understanding and proficiency.
By mastering the technique of simplifying square roots, such as \(\sqrt{50}\), students and enthusiasts can enhance their mathematical problem-solving skills and gain a deeper appreciation for the structure and properties of numbers. Continuous practice and application of these concepts will lead to greater confidence and accuracy in handling square roots and other related mathematical operations.
Tìm hiểu cách đơn giản hóa căn bậc hai của 50 một cách dễ dàng và chính xác. Video hướng dẫn chi tiết để giúp bạn hiểu rõ hơn về quá trình đơn giản hóa căn bậc hai.
Cách Đơn Giản Hóa Căn Bậc Hai Của 50: Căn(50)
READ MORE:
Khám phá cách đơn giản hóa căn bậc hai của một số, đặc biệt là căn(50). Video hướng dẫn chi tiết giúp bạn hiểu rõ hơn về việc đơn giản hóa căn bậc hai trong toán học.
Đơn Giản Hóa Căn Bậc Hai Của Một Số | Đơn Giản Hóa Toán Học, Căn(50)