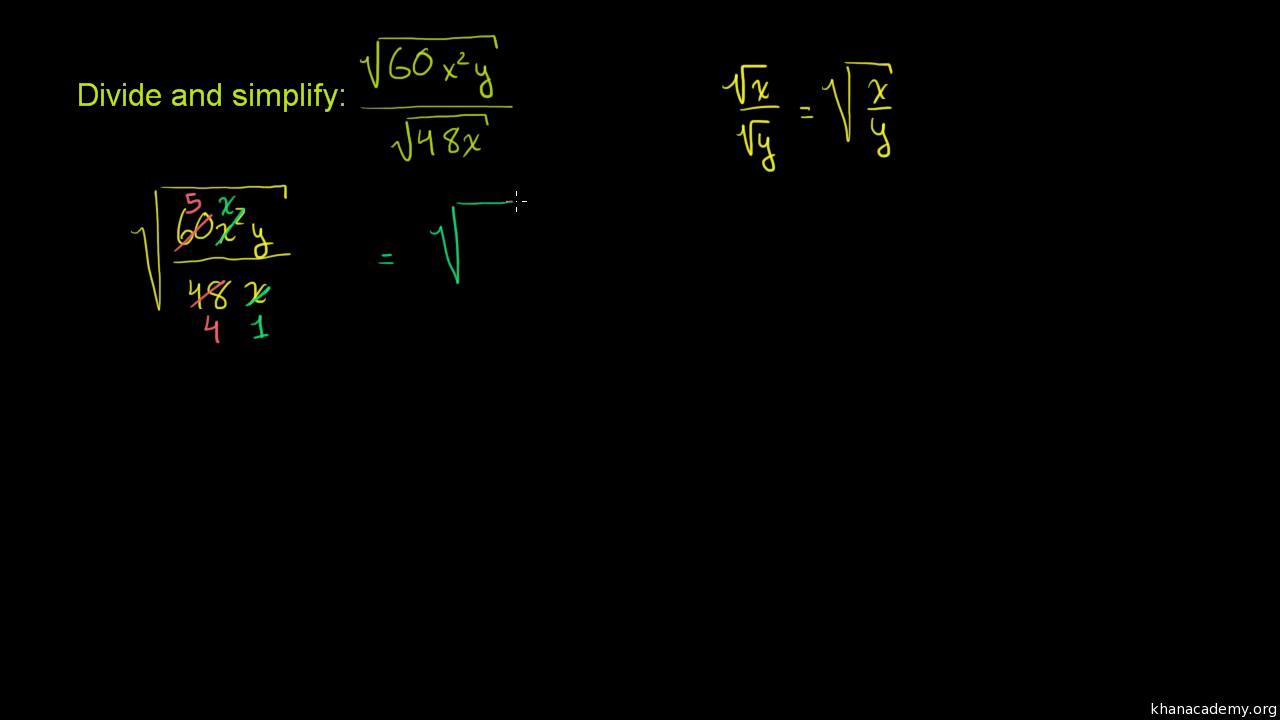Topic simplify radical expressions using the distributive property: Simplifying radical expressions can be straightforward and efficient by using the distributive property. This method allows you to break down complex expressions into simpler parts, making the process more manageable. In this article, we will explore step-by-step techniques and tips to help you master the art of simplifying radical expressions effortlessly.
Table of Content
- Simplifying Radical Expressions Using the Distributive Property
- Introduction to Radical Expressions
- Understanding the Distributive Property
- Basic Concepts of Radicals
- Applying the Distributive Property to Radicals
- Step-by-Step Process for Simplifying Radical Expressions
- Examples of Simplifying Radicals Using the Distributive Property
- Common Mistakes to Avoid
- Tips and Tricks for Simplification
- Advanced Techniques in Radical Simplification
- Practice Problems and Solutions
- Frequently Asked Questions
- Conclusion and Summary
- Additional Resources
- YOUTUBE:
Simplifying Radical Expressions Using the Distributive Property
When simplifying radical expressions, the distributive property can be a valuable tool. This property states that for any numbers \( a \), \( b \), and \( c \):
\( a(b + c) = ab + ac \)
Applying this to radical expressions involves distributing the terms under the radical signs. Here are the steps to follow:
Step-by-Step Process
- Identify the expression under the radical that can be simplified.
- Break down the expression into smaller parts if possible.
- Apply the distributive property by multiplying the terms under the radicals.
- Simplify the resulting expression by combining like terms and simplifying any perfect squares.
Examples
Let's look at a few examples to understand this process better:
Example 1: Simplify \( \sqrt{a(b + c)} \)
According to the distributive property:
\( \sqrt{a(b + c)} = \sqrt{ab + ac} \)
Next, simplify the expression inside the radical if possible.
Example 2: Simplify \( \sqrt{3(2 + 5)} \)
First, distribute inside the radical:
\( \sqrt{3(2 + 5)} = \sqrt{3 \cdot 2 + 3 \cdot 5} = \sqrt{6 + 15} = \sqrt{21} \)
The expression \( \sqrt{21} \) is already in its simplest form as 21 has no perfect square factors other than 1.
Example 3: Simplify \( \sqrt{2(x^2 + 4x)} \)
Distribute the 2 under the radical:
\( \sqrt{2(x^2 + 4x)} = \sqrt{2x^2 + 8x} \)
Since there are no further simplifications possible within the radical, the expression is \( \sqrt{2x^2 + 8x} \).
Tips for Simplification
- Always look for perfect square factors when simplifying radicals.
- Use the distributive property to break down complex expressions into simpler parts.
- Combine like terms and factor where possible to make simplification easier.
By following these steps and tips, you can effectively simplify radical expressions using the distributive property.
READ MORE:
Introduction to Radical Expressions
Radical expressions, often involving square roots, are an integral part of algebra. Understanding these expressions and how to simplify them is essential for solving various mathematical problems. A radical expression includes a radical symbol (√) with an expression inside it, such as √x. Simplifying these expressions can often make complex problems more manageable.
Radicals can be simplified using several methods, one of the most effective being the Distributive Property. This method involves distributing a common factor across terms within the radical expression, similar to how you would distribute a multiplier in an algebraic expression.
Let's explore the step-by-step process of simplifying radical expressions using the distributive property:
-
Identify the Radical Terms:
First, identify the terms within the radical that need to be simplified. For example, in the expression 2(√4 + √10), √4 and √10 are the radical terms.
-
Apply the Distributive Property:
Distribute the factor outside the parentheses to each term inside. For instance, 2(√4 + √10) becomes 2√4 + 2√10.
-
Simplify Each Term:
Simplify the radical terms if possible. In our example, √4 simplifies to 2, so 2√4 becomes 2*2 or 4. Thus, 2(√4 + √10) simplifies to 4 + 2√10.
-
Combine Like Terms:
If there are like terms, combine them. In cases where like terms exist, such as √5(√8 + √10), the expression becomes √5*√8 + √5*√10, which simplifies to √40 + √50, and then further to 2√10 + 5√2.
By following these steps, you can simplify complex radical expressions, making them easier to work with in equations and other mathematical contexts. Mastery of these techniques is crucial for advancing in algebra and higher-level math courses.
Understanding the Distributive Property
The distributive property is a fundamental principle in algebra that allows you to simplify expressions involving both multiplication and addition or subtraction. It states that for any numbers \(a\), \(b\), and \(c\), the equation \(a(b + c) = ab + ac\) holds true. This property can also be applied to expressions involving radicals.
When working with radical expressions, the distributive property helps to simplify and multiply terms efficiently. Here's a step-by-step guide:
- Identify the Expression: Start with the expression where a radical is being multiplied by a binomial. For example, \(\sqrt{3}(2 + \sqrt{5})\).
- Apply the Distributive Property: Distribute the radical to each term inside the parentheses.
- \(\sqrt{3}(2 + \sqrt{5}) = \sqrt{3} \cdot 2 + \sqrt{3} \cdot \sqrt{5}\)
- Multiply the Terms: Perform the multiplication for each term.
- \(\sqrt{3} \cdot 2 = 2\sqrt{3}\)
- \(\sqrt{3} \cdot \sqrt{5} = \sqrt{3 \cdot 5} = \sqrt{15}\)
- Combine Like Terms: Combine any like terms to simplify the expression further. In this example, there are no like terms to combine.
- The final simplified expression is \(2\sqrt{3} + \sqrt{15}\).
The distributive property is especially useful when dealing with more complex expressions and ensures that all terms are accurately accounted for during multiplication.
Here are more examples to illustrate the use of the distributive property with radical expressions:
- \(\sqrt{2}(3 + \sqrt{7}) = 3\sqrt{2} + \sqrt{14}\)
- \(-\sqrt{5}(4 - \sqrt{10}) = -4\sqrt{5} + \sqrt{50} = -4\sqrt{5} + 5\sqrt{2}\)
- \(\sqrt{x}(2 + \sqrt{x}) = 2\sqrt{x} + \sqrt{x^2} = 2\sqrt{x} + x\)
By mastering the distributive property, you can simplify and solve a wide range of algebraic expressions involving radicals, making it a powerful tool in your mathematical toolkit.
Basic Concepts of Radicals
Radicals, often referred to as roots, are mathematical expressions that involve the root of a number. The most common type of radical is the square root, but there are also cube roots, fourth roots, and so on. Understanding the basic concepts of radicals is essential for simplifying radical expressions.
- Square Roots: The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). It is denoted as \( \sqrt{x} \).
- Cube Roots: The cube root of a number \( x \) is a value that, when used in a product three times, gives \( x \). It is denoted as \( \sqrt[3]{x} \).
- Higher-order Roots: These include fourth roots, fifth roots, etc. The \( n \)-th root of a number \( x \) is a value that, when used in a product \( n \) times, gives \( x \). It is denoted as \( \sqrt[n]{x} \).
Radical expressions can often be simplified by using the properties of radicals. These properties include:
- Product Rule: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \)
- Quotient Rule: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
Let's look at some examples to understand these concepts better:
- Simplify \( \sqrt{50} \):
- Factor 50 into its prime factors: \( 50 = 2 \cdot 5^2 \).
- Apply the product rule: \( \sqrt{50} = \sqrt{2 \cdot 5^2} = \sqrt{2} \cdot \sqrt{5^2} = \sqrt{2} \cdot 5 = 5\sqrt{2} \).
- Simplify \( \sqrt[3]{27x^3} \):
- Recognize that 27 is \( 3^3 \) and apply the cube root: \( \sqrt[3]{27x^3} = \sqrt[3]{3^3 \cdot x^3} = 3x \).
- Simplify \( \sqrt[4]{16y^4} \):
- Recognize that 16 is \( 2^4 \) and apply the fourth root: \( \sqrt[4]{16y^4} = \sqrt[4]{2^4 \cdot y^4} = 2y \).
By understanding these basic concepts and properties of radicals, you can simplify complex radical expressions with confidence.
Applying the Distributive Property to Radicals
The distributive property is a powerful tool when working with radical expressions. It allows us to simplify expressions by distributing a common factor across terms inside a radical. Here, we will explore how to apply this property step-by-step to simplify complex radical expressions.
-
Identify the expression: Consider the expression where you need to apply the distributive property. For example,
2(\sqrt{4} + \sqrt{10}) . -
Distribute the factor: Apply the distributive property by multiplying the factor outside the parentheses with each term inside the parentheses:
2 \cdot \sqrt{4} 2 \cdot \sqrt{10}
-
Simplify each term: Calculate the product of each term. For example:
2 \cdot \sqrt{4} = 2 \cdot 2 = 4 2 \cdot \sqrt{10} = 2\sqrt{10}
-
Combine the results: Sum the simplified terms to get the final expression:
4 + 2\sqrt{10}
Let's see another example with a more complex expression,
Distribute
\sqrt{5} :\sqrt{5} \cdot \sqrt{8} = \sqrt{5 \cdot 8} = \sqrt{40} \sqrt{5} \cdot \sqrt{10} = \sqrt{5 \cdot 10} = \sqrt{50}
Simplify the radicals where possible:
\sqrt{40} = \sqrt{4 \cdot 10} = 2\sqrt{10} \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}
Combine the simplified terms:
2\sqrt{10} + 5\sqrt{2}
By following these steps, you can simplify radical expressions efficiently using the distributive property. This method not only makes the expression more manageable but also helps in solving equations that involve radicals.

Step-by-Step Process for Simplifying Radical Expressions
To simplify radical expressions using the distributive property, follow these detailed steps:
-
Identify the Expression: Begin by identifying the radical expression that needs to be simplified. For example, \(2(\sqrt{4} + \sqrt{10})\).
-
Distribute the Multiplier: Use the distributive property to multiply the term outside the parentheses by each term inside the parentheses. This means \(2 \cdot \sqrt{4} + 2 \cdot \sqrt{10}\).
-
Simplify Individual Radicals: Simplify the radicals individually if possible. For example, \(\sqrt{4}\) simplifies to 2, so the expression becomes \(2 \cdot 2 + 2 \cdot \sqrt{10}\).
-
Combine Like Terms: Multiply and combine like terms. Here, it simplifies to \(4 + 2\sqrt{10}\).
-
Final Simplification: Write down the final simplified expression. In this example, the simplified expression is \(4 + 2\sqrt{10}\).
Using these steps will help you simplify any radical expression using the distributive property effectively. Practice with different expressions to master the process!
Examples of Simplifying Radicals Using the Distributive Property
Applying the distributive property to simplify radical expressions involves multiplying a single term by each term inside a parenthesis and then combining like terms. Here are some detailed examples:
Example 1:
Simplify \( \sqrt{5} (\sqrt{8} + \sqrt{10}) \)
- Distribute \( \sqrt{5} \) to each term inside the parenthesis:
- \( \sqrt{5} \cdot \sqrt{8} + \sqrt{5} \cdot \sqrt{10} \)
- Apply the product rule for radicals:
- \( \sqrt{5 \cdot 8} + \sqrt{5 \cdot 10} \)
- Simplify the radicals:
- \( \sqrt{40} + \sqrt{50} \)
- Further simplify by breaking down the radicands into prime factors:
- \( \sqrt{4 \cdot 10} + \sqrt{25 \cdot 2} \)
- \( 2\sqrt{10} + 5\sqrt{2} \)
Example 2:
Simplify \( 2\sqrt{5} (\sqrt{6} + 2) \)
- Distribute \( 2\sqrt{5} \) to each term inside the parenthesis:
- \( 2\sqrt{5} \cdot \sqrt{6} + 2\sqrt{5} \cdot 2 \)
- Apply the product rule for radicals:
- \( 2\sqrt{30} + 4\sqrt{5} \)
Example 3:
Simplify \( \sqrt{14} (3 - \sqrt{4}) \)
- Distribute \( \sqrt{14} \) to each term inside the parenthesis:
- \( \sqrt{14} \cdot 3 - \sqrt{14} \cdot \sqrt{4} \)
- Apply the product rule for radicals:
- \( 3\sqrt{14} - \sqrt{56} \)
- Simplify the radicals:
- \( 3\sqrt{14} - 2\sqrt{14} \)
- Combine like terms:
- \( (3 - 2)\sqrt{14} = \sqrt{14} \)
These examples illustrate how the distributive property can be applied to simplify radical expressions, making complex problems more manageable.
Common Mistakes to Avoid
When simplifying radical expressions using the distributive property, students often encounter several common mistakes. Being aware of these can help you avoid them and ensure your work is accurate. Here are some of the most frequent errors:
-
Forgetting to Distribute to All Terms: One of the most common mistakes is neglecting to apply the distributive property to every term inside the parentheses. For example, in the expression \( a(b + c + d) \), ensure that \( a \) is multiplied by \( b \), \( c \), and \( d \).
Incorrect: \( a(b + c + d) = ab + c + d \)
Correct: \( a(b + c + d) = ab + ac + ad \)
-
Incorrectly Combining Radicals: When multiplying radicals, ensure that you combine them correctly under the same radical sign when applicable. For instance, \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \).
Incorrect: \( \sqrt{2} \cdot \sqrt{8} = \sqrt{16} = 4 \) (This is correct but simplified incorrectly without intermediate steps)
Correct: \( \sqrt{2} \cdot \sqrt{8} = \sqrt{16} = 4 \) (Ensure to show each step clearly)
-
Sign Errors: Pay close attention to positive and negative signs, especially when distributing negative numbers. A common error is to forget that distributing a negative sign changes the signs of all terms within the parentheses.
Incorrect: \( -a(b + c) = -ab + c \)
Correct: \( -a(b + c) = -ab - ac \)
-
Misinterpreting the Radical Multiplication: Be careful with expressions involving multiple radicals. Simplify them step by step to avoid mistakes.
Incorrect: \( \sqrt{a} \cdot \sqrt{b + c} = \sqrt{ab + ac} \)
Correct: \( \sqrt{a} \cdot \sqrt{b + c} = \sqrt{a(b + c)} \)
-
Incorrect Simplification: Ensure that after using the distributive property, you simplify the radicals correctly. This includes breaking down the radicals into their prime factors where possible.
Incorrect: \( \sqrt{50} = 5 \)
Correct: \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \)
Avoiding these common mistakes can greatly enhance your ability to simplify radical expressions accurately. Practice diligently and check each step to ensure correctness.
Tips and Tricks for Simplification
When simplifying radical expressions using the distributive property, certain strategies can make the process more efficient and accurate. Here are some valuable tips and tricks:
-
Understand the Basics:
Before diving into complex expressions, ensure you are comfortable with basic operations involving radicals, such as multiplication, addition, and simplification of individual radicals.
-
Prime Factorization:
Use prime factorization to simplify the radicals wherever possible. Break down the number inside the radical into its prime factors to find and extract perfect squares.
For example:
\(\sqrt{18} = \sqrt{2 \cdot 3^2} = 3\sqrt{2}\)
-
Distribute Carefully:
Apply the distributive property correctly by multiplying each term inside the parenthesis by the term outside. For example, for \(a(b + c)\), distribute as \(ab + ac\).
Example:
\(2(\sqrt{3} + \sqrt{5}) = 2\sqrt{3} + 2\sqrt{5}\)
-
Combine Like Terms:
After distribution, combine like terms to simplify the expression further. This means grouping together terms with the same radical part.
Example:
\(3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2}\)
-
Use Conjugates:
When rationalizing denominators, multiply the numerator and the denominator by the conjugate of the denominator to eliminate radicals in the denominator.
Example:
\(\frac{1}{\sqrt{3} + 1} \cdot \frac{\sqrt{3} - 1}{\sqrt{3} - 1} = \frac{\sqrt{3} - 1}{3 - 1} = \frac{\sqrt{3} - 1}{2}\)
-
Simplify Step-by-Step:
Break down the problem into smaller, manageable steps. Simplify each part of the expression before combining them. This methodical approach helps in avoiding errors.
-
Double-Check Your Work:
After simplifying the expression, revisit each step to ensure that no mistakes were made. This includes verifying that all like terms are combined and that all radicals are simplified.
-
Practice Regularly:
Regular practice is key to mastering simplification of radical expressions. Work on various problems to become comfortable with different types of expressions and their simplification methods.
By following these tips and tricks, you can streamline the process of simplifying radical expressions and improve your accuracy and confidence in handling such problems.
Advanced Techniques in Radical Simplification
Advanced techniques in radical simplification often involve leveraging various properties and rules of radicals. These methods can make complex expressions more manageable and easier to work with.
- Using Higher-Order Roots:
When simplifying higher-order roots, such as cube roots or fourth roots, recognize that these roots can be broken down using the product rule. For example, to simplify \( \sqrt[3]{27x^3} \), use the fact that \( \sqrt[3]{27} = 3 \) and \( \sqrt[3]{x^3} = x \), giving the result \( 3x \).
- Rationalizing the Denominator:
When dealing with radical expressions in the denominator, multiply both the numerator and the denominator by a conjugate or appropriate radical to eliminate the radical from the denominator. For example:
\[
\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\] - Combining Like Terms:
Combine radicals with the same index and radicand by adding or subtracting the coefficients. For instance:
\[
3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}
\] - Using Algebraic Identities:
Apply algebraic identities to simplify expressions involving radicals. For example, use the difference of squares identity:
\[
(a + \sqrt{b})(a - \sqrt{b}) = a^2 - b
\]For instance:
\[
(\sqrt{3} + 2)(\sqrt{3} - 2) = 3 - 4 = -1
\] - Working with Nested Radicals:
When encountering nested radicals, such as \( \sqrt{2 + \sqrt{3}} \), use substitution or algebraic manipulation to simplify. For example, let \( x = \sqrt{2 + \sqrt{3}} \). Squaring both sides gives \( x^2 = 2 + \sqrt{3} \), and further manipulation can simplify the expression.
By mastering these advanced techniques, you can tackle more complex radical expressions and streamline the simplification process.
Practice Problems and Solutions
Here are some practice problems to help you master simplifying radical expressions using the distributive property. Each problem is followed by a detailed solution to aid your understanding.
-
Simplify: \( 2(\sqrt{4} + \sqrt{10}) \)
Solution:
- \( 2(\sqrt{4} + \sqrt{10}) = 2 \cdot \sqrt{4} + 2 \cdot \sqrt{10} \)
- \( 2(\sqrt{4} + \sqrt{10}) = 2 \cdot 2 + 2 \cdot \sqrt{10} \)
- \( 2(\sqrt{4} + \sqrt{10}) = 4 + 2\sqrt{10} \)
-
Simplify: \( \sqrt{5}(\sqrt{8} + \sqrt{10}) \)
Solution:
- \( \sqrt{5}(\sqrt{8} + \sqrt{10}) = \sqrt{5} \cdot \sqrt{8} + \sqrt{5} \cdot \sqrt{10} \)
- \( \sqrt{5}(\sqrt{8} + \sqrt{10}) = \sqrt{40} + \sqrt{50} \)
- \( \sqrt{5}(\sqrt{8} + \sqrt{10}) = 2\sqrt{10} + 5\sqrt{2} \)
-
Simplify: \( \sqrt{3}(\sqrt{9} + \sqrt{21}) \)
Solution:
- \( \sqrt{3}(\sqrt{9} + \sqrt{21}) = \sqrt{3} \cdot \sqrt{9} + \sqrt{3} \cdot \sqrt{21} \)
- \( \sqrt{3}(\sqrt{9} + \sqrt{21}) = 3\sqrt{3} + \sqrt{63} \)
- \( \sqrt{3}(\sqrt{9} + \sqrt{21}) = 3\sqrt{3} + 3\sqrt{7} \)
-
Simplify: \( 2\sqrt{5}(\sqrt{6} + 2) \)
Solution:
- \( 2\sqrt{5}(\sqrt{6} + 2) = 2\sqrt{5} \cdot \sqrt{6} + 2\sqrt{5} \cdot 2 \)
- \( 2\sqrt{5}(\sqrt{6} + 2) = 2\sqrt{30} + 4\sqrt{5} \)
-
Simplify: \( \sqrt{14}(3 - \sqrt{4}) \)
Solution:
- \( \sqrt{14}(3 - \sqrt{4}) = \sqrt{14} \cdot 3 - \sqrt{14} \cdot \sqrt{4} \)
- \( \sqrt{14}(3 - \sqrt{4}) = 3\sqrt{14} - 2\sqrt{14} \)
- \( \sqrt{14}(3 - \sqrt{4}) = \sqrt{14} \)
-
Simplify: \( \sqrt{21}(5 + \sqrt{7}) \)
Solution:
- \( \sqrt{21}(5 + \sqrt{7}) = \sqrt{21} \cdot 5 + \sqrt{21} \cdot \sqrt{7} \)
- \( \sqrt{21}(5 + \sqrt{7}) = 5\sqrt{21} + \sqrt{147} \)
- \( \sqrt{21}(5 + \sqrt{7}) = 5\sqrt{21} + 7\sqrt{3} \)
-
Simplify: \( (5 - \sqrt{3})(5 + \sqrt{3}) \)
Solution:
- Using the algebraic identity \( (a + b)(a - b) = a^2 - b^2 \)
- \( (5 - \sqrt{3})(5 + \sqrt{3}) = 5^2 - (\sqrt{3})^2 \)
- \( (5 - \sqrt{3})(5 + \sqrt{3}) = 25 - 3 \)
- \( (5 - \sqrt{3})(5 + \sqrt{3}) = 22 \)
Frequently Asked Questions
-
Q: What is the Distributive Property and how is it used in simplifying radical expressions?
A: The Distributive Property states that \(a(b + c) = ab + ac\). When applied to radical expressions, this property allows us to distribute a factor across terms inside the parentheses. For example, to simplify \(2(\sqrt{3} + \sqrt{5})\), you would apply the property as follows: \(2 \cdot \sqrt{3} + 2 \cdot \sqrt{5} = 2\sqrt{3} + 2\sqrt{5}\).
-
Q: Can you provide an example of using the Distributive Property to simplify a more complex radical expression?
A: Sure! Consider the expression \(\sqrt{2}(3\sqrt{3} + 5\sqrt{6})\). Using the Distributive Property, we get:
\[
\sqrt{2} \cdot 3\sqrt{3} + \sqrt{2} \cdot 5\sqrt{6} = 3\sqrt{6} + 5\sqrt{12}.
\]
Further simplifying, \(5\sqrt{12} = 5 \cdot 2\sqrt{3} = 10\sqrt{3}\). Thus, the expression simplifies to:
\[
3\sqrt{6} + 10\sqrt{3}.
\] -
Q: What are some common mistakes to avoid when simplifying radical expressions using the Distributive Property?
A: Some common mistakes include:
- Forgetting to multiply the coefficient outside the parentheses by each term inside the parentheses.
- Incorrectly simplifying the radicals after applying the Distributive Property. Always ensure the radicals are fully simplified.
- Not combining like terms when possible. Always check if the resulting terms can be combined for further simplification.
Q: How do you handle expressions with multiple radicals and coefficients?
A: When dealing with multiple radicals and coefficients, apply the Distributive Property step-by-step. For example:
\[
2\sqrt{3}(4\sqrt{2} + \sqrt{5}) = 2\sqrt{3} \cdot 4\sqrt{2} + 2\sqrt{3} \cdot \sqrt{5} = 8\sqrt{6} + 2\sqrt{15}.
\]
Each term is handled separately before combining them in the final simplified expression.-
Q: What should I do if the expression inside the parentheses cannot be simplified further?
A: If the expression inside the parentheses cannot be simplified further, you simply apply the Distributive Property and leave the terms as they are. For example, \(3(\sqrt{2} + \sqrt{3})\) becomes \(3\sqrt{2} + 3\sqrt{3}\), which is the simplest form.
Conclusion and Summary
In conclusion, simplifying radical expressions using the distributive property is a powerful technique that enhances our ability to work with and understand these mathematical forms. By mastering this method, we can break down complex expressions into simpler, more manageable components. Here are the key takeaways:
- Distributive Property Application: The distributive property allows us to multiply a single term by each term within a parenthesis, effectively distributing the multiplication across all terms.
- Combining Like Terms: When simplifying radicals, it is essential to combine like terms by adding or subtracting the coefficients of the radicals with the same radicand.
- Rationalizing the Denominator: Use the distributive property to eliminate radicals from the denominator by multiplying by the conjugate of the denominator.
- Advanced Techniques: Techniques such as rationalizing denominators and using algebraic identities like \( (a+b)(a-b) = a^2 - b^2 \) can simplify complex radical expressions.
By applying these principles, we can solve a wide range of problems involving radical expressions efficiently. Practice and familiarity with these techniques will lead to greater confidence and proficiency in handling radical expressions in algebra and beyond.
We encourage you to continue practicing these methods through various problems and to explore additional resources for further learning and application. Remember, the more you practice, the more intuitive these processes will become.
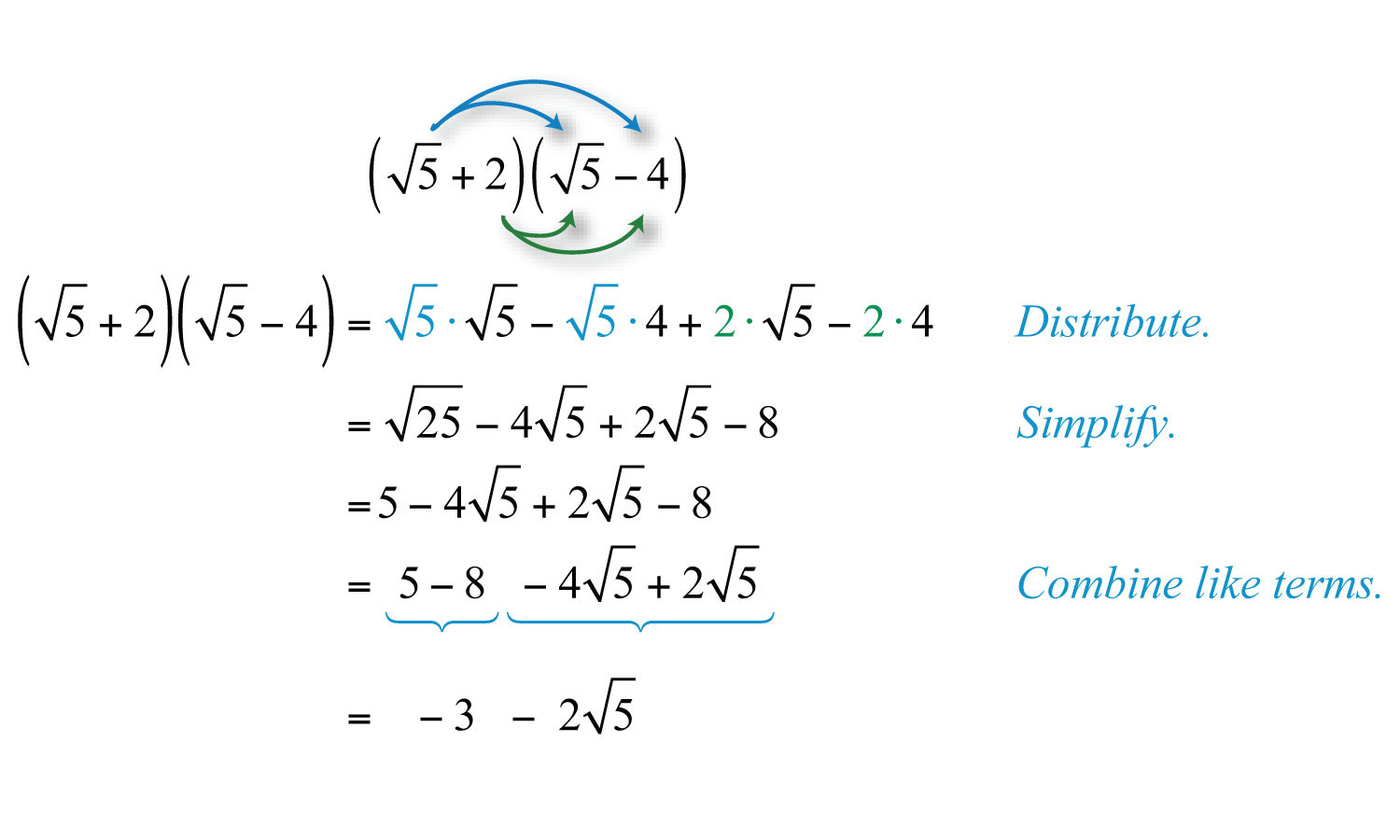
Additional Resources
For further study and practice on simplifying radical expressions using the distributive property, consider the following resources:
-
Online Math Tutorials: Websites such as offer comprehensive tutorials and practice problems that can help you master the techniques for simplifying radicals.
-
Interactive Practice: Utilize interactive math platforms like for step-by-step tutorials and practice exercises on radical expressions and other algebraic concepts.
-
Math Forums and Communities: Engage with online math communities such as where you can ask questions, share solutions, and learn from others.
-
Educational Videos: Watch educational videos on platforms like for visual and auditory learning experiences. Channels like and provide detailed explanations and examples.
-
Textbooks and Workbooks: Refer to algebra textbooks and workbooks which include sections on radicals and the distributive property. Books like "Algebra and Trigonometry" by Michael Sullivan are great resources.
-
Math Software: Use math software tools like for computational assistance and verifying your solutions.
-
Tutoring Services: If you need personalized help, consider online tutoring services like or local tutoring centers.
These resources can provide additional explanations, examples, and practice opportunities to enhance your understanding and proficiency in simplifying radical expressions using the distributive property.
Sử dụng Tính Chất Phân Phối để Đơn Giản Hóa Biểu Thức với Căn Bậc Hai
READ MORE:
Đại số - Chương 22: Sản Phẩm và Thương của Biểu Thức Căn Bậc Hai (1 trong 11) Tính Chất Phân Phối