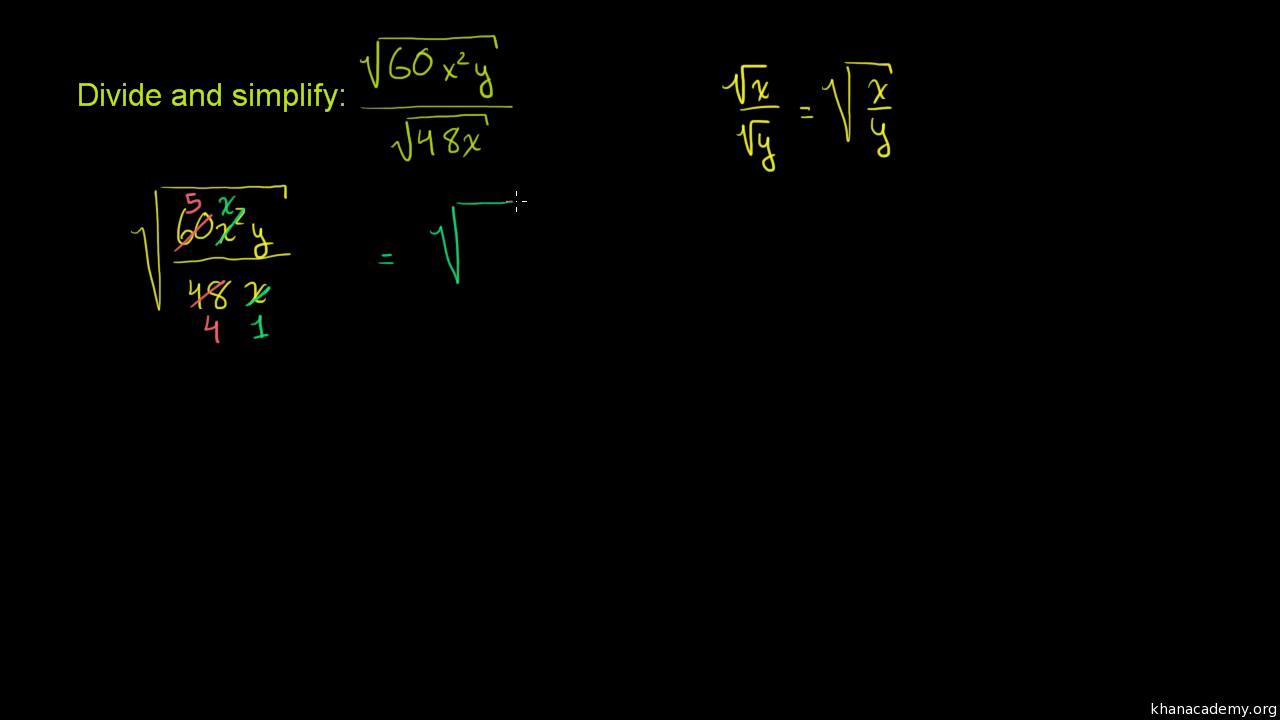Topic multiplying and simplifying radical expressions: Discover the secrets to mastering multiplying and simplifying radical expressions with our comprehensive guide. Learn step-by-step methods, practical examples, and tips to simplify even the most complex radicals. Perfect for students and math enthusiasts looking to enhance their skills and confidence in handling radical expressions.
Table of Content
- Multiplying and Simplifying Radical Expressions
- Introduction
- Understanding Radicals
- Basic Properties of Radicals
- Multiplying Radical Expressions
- Distributive Property and FOIL Method
- Combining Like Terms
- Examples of Multiplying Radicals
- Rationalizing the Denominator
- Complex Radical Expressions
- Practice Problems and Solutions
- YOUTUBE: Hướng dẫn chi tiết cách nhân các biểu thức căn bậc hai với biến và số mũ. Tìm hiểu các bước đơn giản và hiệu quả để thực hiện phép tính này.
Multiplying and Simplifying Radical Expressions
When working with radical expressions, it is often necessary to multiply and simplify them. The process involves applying the distributive property, combining like terms, and simplifying the radicals.
Multiplying Radicals
To multiply radical expressions, follow these steps:
- Multiply the coefficients (numbers outside the radical).
- Multiply the radicands (numbers inside the radical).
- Simplify the resulting expression if possible.
Example:
\[
(3\sqrt{2})(2\sqrt{5}) = 3 \cdot 2 \cdot \sqrt{2 \cdot 5} = 6\sqrt{10}
\]
Using the Distributive Property
When multiplying expressions with multiple terms, use the distributive property (also known as FOIL for binomials).
Example:
\[
(\sqrt{x} + \sqrt{y})(\sqrt{x} - \sqrt{y}) = \sqrt{x} \cdot \sqrt{x} + \sqrt{x} \cdot (-\sqrt{y}) + \sqrt{y} \cdot \sqrt{x} + \sqrt{y} \cdot (-\sqrt{y})
\]
\[
= x - \sqrt{xy} + \sqrt{xy} - y = x - y
\]
Simplifying Radicals
After multiplying, you often need to simplify the resulting radical. Look for perfect squares (or cubes for cube roots) in the radicand.
Example:
\[
\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}
\]
Examples of Multiplying and Simplifying
Example 1:
Multiply and simplify:
\[
(\sqrt{3} + 2)(\sqrt{3} - 1)
\]
Solution:
\[
= \sqrt{3} \cdot \sqrt{3} + \sqrt{3} \cdot (-1) + 2 \cdot \sqrt{3} + 2 \cdot (-1)
= 3 - \sqrt{3} + 2\sqrt{3} - 2
= 1 + \sqrt{3}
\]
Example 2:
Multiply and simplify:
\[
(2\sqrt{5} + 3)(\sqrt{5} - 4)
\]
Solution:
\[
= 2\sqrt{5} \cdot \sqrt{5} + 2\sqrt{5} \cdot (-4) + 3 \cdot \sqrt{5} + 3 \cdot (-4)
= 10 - 8\sqrt{5} + 3\sqrt{5} - 12
= -2 - 5\sqrt{5}
\]
Example 3:
Simplify:
\[
\sqrt[3]{x^5} \cdot \sqrt[3]{x^2} = \sqrt[3]{x^5 \cdot x^2} = \sqrt[3]{x^7} = x^2 \sqrt[3]{x}
\]
Conclusion
Multiplying and simplifying radical expressions involve a few straightforward steps. By understanding the rules for multiplying radicals and practicing the simplification process, you can master these types of problems.

READ MORE:
Introduction
Radical expressions often involve roots, such as square roots or cube roots. Multiplying and simplifying these expressions requires a good understanding of the properties of radicals and algebraic operations. By learning these techniques, you can solve complex mathematical problems more efficiently.
To multiply radical expressions, follow these steps:
- Multiply the coefficients (numbers outside the radicals).
- Multiply the radicands (numbers inside the radicals) together.
- Simplify the resulting radical expression if possible.
Simplifying radical expressions often involves breaking down the radicand into its prime factors and looking for perfect squares or cubes that can be simplified. This process can make the expression easier to work with and understand.
For example, to multiply and simplify the expression
This shows that the product of two radicals can often be simplified to a simpler form.
Throughout this section, we will explore various examples and techniques for multiplying and simplifying radical expressions, providing a solid foundation for tackling more complex algebraic problems.
Understanding Radicals
Radicals are mathematical expressions that involve roots, such as square roots, cube roots, etc. Simplifying radicals involves reducing the expression under the radical sign to its simplest form. Here are some key concepts and steps to understand radicals:
- Radicand: The number or expression inside the radical symbol.
- Index: The small number outside and to the left of the radical symbol that indicates the degree of the root.
- Radical Symbol: The symbol √ used to denote roots.
Steps to Simplify Radicals
- Prime Factorization: Break down the number under the radical into its prime factors.
- Grouping Factors: Group the prime factors into pairs (for square roots) or other group sizes based on the index of the root.
- Simplify the Radical: Bring one factor out of the radical for each complete group formed.
For example, to simplify \(\sqrt{72}\), we follow these steps:
- Prime factorize 72: \(72 = 2^3 \times 3^2\)
- Group the factors: \(\sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 2) \times 3^2} = \sqrt{4 \times 2 \times 9}\)
- Simplify: \(\sqrt{4 \times 2 \times 9} = \sqrt{4} \times \sqrt{2} \times \sqrt{9} = 2 \sqrt{2} \times 3 = 6\sqrt{2}\)
Therefore, \(\sqrt{72} = 6\sqrt{2}\).
Properties of Radicals
- \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \neq 0\)
- \(\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\)
- \(\sqrt{a} - \sqrt{b} \neq \sqrt{a - b}\)
Understanding these properties and steps helps in simplifying and manipulating radical expressions effectively.
Basic Properties of Radicals
Understanding the basic properties of radicals is essential for simplifying and manipulating radical expressions. Here are some key properties:
- Product Property: For any non-negative real numbers \(a\) and \(b\), and any positive integer \(n\), \(\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}\). This property allows us to combine radicals with the same index.
- Quotient Property: For any non-negative real numbers \(a\) and \(b\), and any positive integer \(n\), \(\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\). This property is useful for simplifying fractions under a radical.
- Power of a Power Property: For any real number \(a\) and positive integers \(m\) and \(n\), \(\left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m}\). This property helps in raising radicals to a power.
- Simplifying Radicals: A radical is in its simplest form when the radicand has no perfect power factors other than 1. For example, \(\sqrt{18}\) can be simplified to \(3\sqrt{2}\) because 18 = 9 * 2 and \(\sqrt{9} = 3\).
These properties form the foundation for working with radical expressions, making it easier to perform operations like multiplication, division, and simplification.
| Property | Formula | Example |
|---|---|---|
| Product Property | \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\) | \(\sqrt{3} \cdot \sqrt{12} = \sqrt{36} = 6\) |
| Quotient Property | \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) | \(\sqrt{\frac{16}{4}} = \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2\) |
| Power of a Power | \(\left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m}\) | \(\left(\sqrt[3]{2}\right)^3 = \sqrt[3]{2^3} = \sqrt[3]{8} = 2\) |
| Simplifying Radicals | N/A | \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\) |
Multiplying Radical Expressions
Multiplying radical expressions involves several steps to ensure accuracy and simplification. Below is a detailed, step-by-step guide to help you master this process:
-
Identify Like Radicals: Ensure the radicals you are multiplying have the same index and radicand. If they do, you can proceed with multiplication.
-
Multiply the Coefficients: Multiply the numbers outside the radical signs (coefficients) together.
- Example: \(3 \sqrt{2} \times 4 \sqrt{2} = (3 \times 4) \sqrt{2 \times 2} = 12 \sqrt{4}\)
-
Multiply the Radicands: Multiply the numbers inside the radical signs (radicands) together.
- Example: \( \sqrt{3} \times \sqrt{6} = \sqrt{3 \times 6} = \sqrt{18}\)
-
Simplify the Radical: Simplify the resulting radical expression by finding and extracting perfect squares.
- Example: \( \sqrt{18} = \sqrt{9 \times 2} = 3 \sqrt{2}\)
-
Combine Like Terms: If there are like terms, combine them to further simplify the expression.
- Example: \(12 \sqrt{4} = 12 \times 2 = 24\)
Here's an example to illustrate these steps in action:
Example: Multiply \(3 \sqrt{5} \times 2 \sqrt{10}\)
- Multiply the coefficients: \(3 \times 2 = 6\)
- Multiply the radicands: \( \sqrt{5} \times \sqrt{10} = \sqrt{50}\)
- Simplify the radical: \( \sqrt{50} = \sqrt{25 \times 2} = 5 \sqrt{2}\)
- Combine the results: \(6 \times 5 \sqrt{2} = 30 \sqrt{2}\)
Thus, \(3 \sqrt{5} \times 2 \sqrt{10} = 30 \sqrt{2}\).
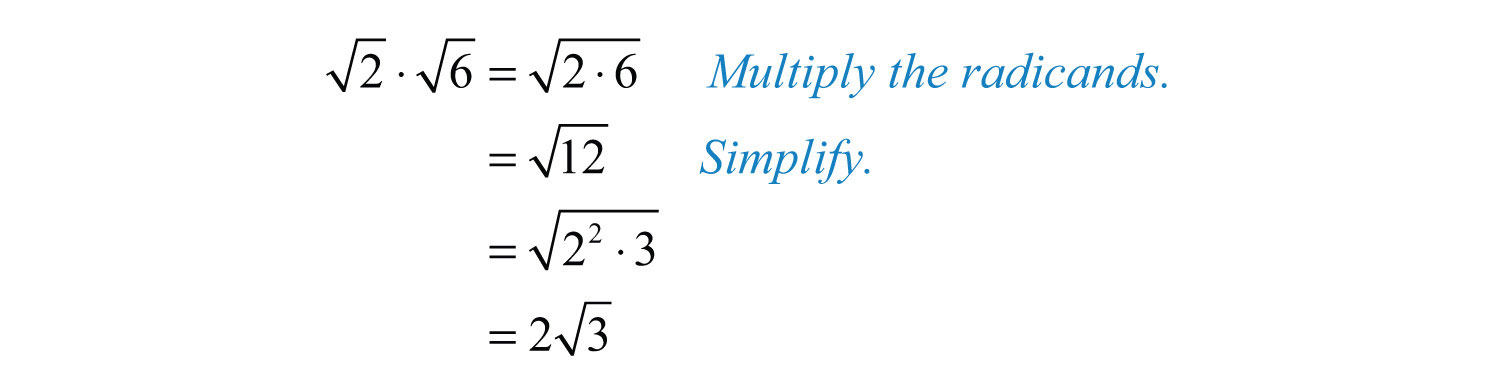
Distributive Property and FOIL Method
The distributive property and the FOIL method are essential tools for multiplying and simplifying radical expressions. Understanding these methods will help simplify complex algebraic problems and ensure accurate results.
Distributive Property
The distributive property allows you to distribute a multiplier to each term within parentheses. For example, to simplify \(a(b + c)\), apply the multiplier \(a\) to both \(b\) and \(c\):
- \(a \cdot b + a \cdot c\)
When dealing with multiple terms, the distributive property can be applied iteratively:
\((a + b)(c + d)\) becomes \(a(c + d) + b(c + d)\)
Next, distribute each term individually:
- \(a \cdot c + a \cdot d + b \cdot c + b \cdot d\)
FOIL Method
The FOIL method is a specific application of the distributive property for binomials, where FOIL stands for First, Outside, Inside, and Last. To multiply \((a + b)(c + d)\), apply these steps:
- First: Multiply the first terms of each binomial \(a \cdot c\)
- Outside: Multiply the outer terms \(a \cdot d\)
- Inside: Multiply the inner terms \(b \cdot c\)
- Last: Multiply the last terms \(b \cdot d\)
Combine these products to get the final result:
- \(a \cdot c + a \cdot d + b \cdot c + b \cdot d\)
For example, to multiply \((2x + 3)(4x - 5)\):
- First: \(2x \cdot 4x = 8x^2\)
- Outside: \(2x \cdot -5 = -10x\)
- Inside: \(3 \cdot 4x = 12x\)
- Last: \(3 \cdot -5 = -15\)
Combine these to get:
- \(8x^2 - 10x + 12x - 15\)
- Simplify by combining like terms: \(8x^2 + 2x - 15\)
Combining Like Terms
Combining like terms in radical expressions is a crucial step in simplifying and solving equations involving radicals. Like terms are terms that have the same radical part. Here’s how to combine them effectively:
- Identify Like Terms: Look for terms that have the same radical part. For instance, in the expression \(3\sqrt{2} + 5\sqrt{2} - 2\sqrt{3}\), \(3\sqrt{2}\) and \(5\sqrt{2}\) are like terms, while \(-2\sqrt{3}\) is not.
- Add or Subtract the Coefficients: Once you've identified the like terms, combine them by adding or subtracting their coefficients. For example:
- \(3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2}\)
- \(7\sqrt{5} - 2\sqrt{5} = (7 - 2)\sqrt{5} = 5\sqrt{5}\)
- Simplify the Expression: After combining the like terms, write the simplified expression. For example:
- Given the expression \(4\sqrt{3} + 6\sqrt{3} - 2\sqrt{2}\), combine the like terms to get:
- \(4\sqrt{3} + 6\sqrt{3} = 10\sqrt{3}\)
- The expression simplifies to \(10\sqrt{3} - 2\sqrt{2}\).
- Given the expression \(4\sqrt{3} + 6\sqrt{3} - 2\sqrt{2}\), combine the like terms to get:
It is important to remember that you can only combine terms with the same radical part. If the radicals are different, they cannot be combined.
| Expression | Simplified Form |
|---|---|
| \(3\sqrt{7} + 2\sqrt{7}\) | \(5\sqrt{7}\) |
| \(4\sqrt{5} - 3\sqrt{5}\) | \(\sqrt{5}\) |
| \(2\sqrt{3} + 6\sqrt{2}\) | Cannot be combined |
Examples of Multiplying Radicals
Understanding how to multiply radical expressions is essential for simplifying and solving various algebraic problems. Here are a few detailed examples to illustrate the process:
-
Example 1: Multiply \(\sqrt{3} \cdot \sqrt{12}\)
- Combine the radicals: \(\sqrt{3 \cdot 12}\)
- Simplify inside the radical: \(\sqrt{36}\)
- Find the square root: \(6\)
Result: \(\sqrt{3} \cdot \sqrt{12} = 6\)
-
Example 2: Multiply \(\sqrt{5x} \cdot \sqrt{20x^3}\)
- Combine the radicals: \(\sqrt{5x \cdot 20x^3}\)
- Simplify inside the radical: \(\sqrt{100x^4}\)
- Find the square root: \(10x^2\)
Result: \(\sqrt{5x} \cdot \sqrt{20x^3} = 10x^2\)
-
Example 3: Multiply \(2\sqrt{7} \cdot 3\sqrt{14}\)
- Multiply the coefficients: \(2 \cdot 3 = 6\)
- Combine the radicals: \(\sqrt{7 \cdot 14}\)
- Simplify inside the radical: \(\sqrt{98}\)
- Simplify the radical: \(\sqrt{49 \cdot 2} = 7\sqrt{2}\)
- Combine the simplified terms: \(6 \cdot 7\sqrt{2} = 42\sqrt{2}\)
Result: \(2\sqrt{7} \cdot 3\sqrt{14} = 42\sqrt{2}\)
-
Example 4: Multiply \(\sqrt[3]{2} \cdot \sqrt[3]{16}\)
- Combine the radicals: \(\sqrt[3]{2 \cdot 16}\)
- Simplify inside the radical: \(\sqrt[3]{32}\)
- Find the cube root: \(2\sqrt[3]{4}\)
Result: \(\sqrt[3]{2} \cdot \sqrt[3]{16} = 2\sqrt[3]{4}\)
-
Example 5: Multiply \(\sqrt{a^2 b} \cdot \sqrt{ab^2}\)
- Combine the radicals: \(\sqrt{a^2 b \cdot ab^2}\)
- Simplify inside the radical: \(\sqrt{a^3 b^3}\)
- Rewrite as a product of perfect squares: \(\sqrt{(a b)^3} = (ab)\sqrt{ab}\)
Result: \(\sqrt{a^2 b} \cdot \sqrt{ab^2} = ab\sqrt{ab}\)
Rationalizing the Denominator
Rationalizing the denominator involves rewriting a fraction so that the denominator no longer contains a radical. This process is essential because it is often preferable to have a rational number in the denominator for clarity and simplicity in mathematical expressions.
Follow these steps to rationalize the denominator:
- Identify the Radical: Determine the radical in the denominator that needs to be rationalized.
- Multiply by the Conjugate (if applicable): If the denominator is a binomial with a radical, multiply both the numerator and denominator by the conjugate of the denominator. The conjugate is formed by changing the sign between the two terms.
- Simplify: Multiply out the terms in both the numerator and the denominator. In the denominator, the radicals should eliminate each other, leaving a rational number.
- Reduce the Fraction: Simplify the fraction, if possible, by dividing both the numerator and the denominator by their greatest common divisor.
Here is an example:
Simplify the expression \( \frac{5}{\sqrt{3}} \):
- Multiply the numerator and the denominator by \( \sqrt{3} \) to get:
- The denominator is now rationalized.
\( \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5\sqrt{3}}{3} \)
For a more complex example, consider rationalizing \( \frac{4}{2 + \sqrt{5}} \):
- Multiply the numerator and the denominator by the conjugate of the denominator, \( 2 - \sqrt{5} \):
- Simplify the numerator:
- Simplify the denominator using the difference of squares:
- The final expression is:
\( \frac{4(2 - \sqrt{5})}{(2 + \sqrt{5})(2 - \sqrt{5})} \)
\( 8 - 4\sqrt{5} \)
\( 4 - 5 = -1 \)
\( \frac{8 - 4\sqrt{5}}{-1} = -8 + 4\sqrt{5} \)
By following these steps, you can effectively rationalize the denominator in radical expressions.

Complex Radical Expressions
Complex radical expressions involve combinations of multiple radical terms and require careful manipulation to simplify. In this section, we will explore techniques to handle these expressions effectively.
Combining Radicals with Different Indices
To combine radicals with different indices, we need to find a common index. Consider the following example:
\(\sqrt[3]{2} \times \sqrt[4]{5}\). To simplify this, we first convert them to a common index:
\[\sqrt[3]{2} = 2^{1/3}\] \[\sqrt[4]{5} = 5^{1/4}\]
The least common multiple of 3 and 4 is 12, so we rewrite these as:
\[2^{1/3} = 2^{4/12}\] \[5^{1/4} = 5^{3/12}\]
Now, combining them under a single radical:
\[(2^{4/12} \times 5^{3/12}) = \sqrt[12]{2^4 \times 5^3} = \sqrt[12]{16 \times 125} = \sqrt[12]{2000}\]
Simplifying Nested Radicals
Nested radicals can often be simplified by expressing them in a more manageable form. For example, consider \(\sqrt{2 + \sqrt{3}}\).
Assume it can be written as a single square root: \(\sqrt{a} + \sqrt{b}\). Squaring both sides, we get:
\[(\sqrt{a} + \sqrt{b})^2 = 2 + \sqrt{3}\]
Expanding the left side, we obtain:
\[a + b + 2\sqrt{ab} = 2 + \sqrt{3}\]
By comparing both sides, we can deduce that:
\[a + b = 2\] \[2\sqrt{ab} = \sqrt{3}\]
Solving these equations gives us the values of \(a\) and \(b\).
Operations with Radical Expressions
When dealing with complex radical expressions, it is essential to remember basic operations such as addition, subtraction, multiplication, and division. For instance:
\[\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\] \[\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\] \[\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\] (in most cases)
Examples
Let's look at a few examples to illustrate the concepts:
Simplify \(\sqrt{50} + 2\sqrt{2}\)
Solution: \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\), so the expression becomes \(5\sqrt{2} + 2\sqrt{2} = 7\sqrt{2}\).
Simplify \(\sqrt{18} \times \sqrt{12}\)
Solution: \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\) and \(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\). Therefore, \(\sqrt{18} \times \sqrt{12} = 3\sqrt{2} \times 2\sqrt{3} = 6\sqrt{6}\).
Practice Problems
Try solving the following problems to reinforce your understanding:
- Simplify \(\sqrt[3]{27} \times \sqrt[4]{16}\).
- Simplify \(\sqrt{3 + 2\sqrt{2}}\).
- Combine \(\sqrt{8} + 2\sqrt{2}\).
- Simplify \(\sqrt{72} \times \sqrt{2}\).
In conclusion, working with complex radical expressions requires a solid understanding of basic radical operations and the ability to manipulate expressions to simplify them. With practice, these techniques will become more intuitive.
Practice Problems and Solutions
Below are some practice problems involving multiplying and simplifying radical expressions. Work through each problem step-by-step and check the provided solutions to verify your understanding.
-
Problem: Multiply and simplify \(2\sqrt{3} \cdot 5\sqrt{2}\)
Solution:
- Step 1: Multiply the coefficients: \(2 \cdot 5 = 10\)
- Step 2: Multiply the radicands: \(\sqrt{3} \cdot \sqrt{2} = \sqrt{6}\)
- Final Answer: \(10\sqrt{6}\)
-
Problem: Multiply and simplify \((2\sqrt{3} + \sqrt{5})(\sqrt{3} - 2\sqrt{5})\)
Solution:
- Step 1: Apply the distributive property (FOIL method):
- First: \(2\sqrt{3} \cdot \sqrt{3} = 2 \cdot 3 = 6\)
- Outer: \(2\sqrt{3} \cdot -2\sqrt{5} = -4\sqrt{15}\)
- Inner: \(\sqrt{5} \cdot \sqrt{3} = \sqrt{15}\)
- Last: \(\sqrt{5} \cdot -2\sqrt{5} = -2 \cdot 5 = -10\)
- Step 2: Combine like terms: \(6 - 10 - 4\sqrt{15} + \sqrt{15} = -4 - 3\sqrt{15}\)
- Final Answer: \(-4 - 3\sqrt{15}\)
- Step 1: Apply the distributive property (FOIL method):
-
Problem: Simplify \(\sqrt{50} + 3\sqrt{2} - \sqrt{18}\)
Solution:
- Step 1: Simplify each radical:
- \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\)
- Step 2: Combine like terms: \(5\sqrt{2} + 3\sqrt{2} - 3\sqrt{2} = 5\sqrt{2}\)
- Final Answer: \(5\sqrt{2}\)
- Step 1: Simplify each radical:
-
Problem: Rationalize the denominator and simplify \(\frac{3\sqrt{2}}{\sqrt{5}}\)
Solution:
- Step 1: Multiply the numerator and the denominator by \(\sqrt{5}\): \(\frac{3\sqrt{2} \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}}\)
- Step 2: Simplify: \(\frac{3\sqrt{10}}{5}\)
- Final Answer: \(\frac{3\sqrt{10}}{5}\)
-
Problem: Multiply and simplify \((\sqrt{7} + 2)(\sqrt{7} - 3)\)
Solution:
- Step 1: Apply the distributive property (FOIL method):
- First: \(\sqrt{7} \cdot \sqrt{7} = 7\)
- Outer: \(\sqrt{7} \cdot -3 = -3\sqrt{7}\)
- Inner: \(2 \cdot \sqrt{7} = 2\sqrt{7}\)
- Last: \(2 \cdot -3 = -6\)
- Step 2: Combine like terms: \(7 - 6 - 3\sqrt{7} + 2\sqrt{7} = 1 - \sqrt{7}\)
- Final Answer: \(1 - \sqrt{7}\)
- Step 1: Apply the distributive property (FOIL method):
These problems provide a variety of scenarios to practice multiplying and simplifying radical expressions. Make sure to understand each step and try solving similar problems on your own for better mastery.
Hướng dẫn chi tiết cách nhân các biểu thức căn bậc hai với biến và số mũ. Tìm hiểu các bước đơn giản và hiệu quả để thực hiện phép tính này.
Nhân Các Biểu Thức Căn Bậc Hai Với Biến Và Số Mũ
READ MORE:
Hướng dẫn chi tiết cách nhân các biểu thức căn bậc hai và sau đó đơn giản hóa. Tìm hiểu các bước để thực hiện phép tính này một cách dễ dàng và hiệu quả.
Nhân Các Biểu Thức Căn Bậc Hai và Sau Đó Đơn Giản Hóa