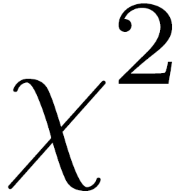How to Solve for x Squared - A Comprehensive Guide

Here is a synthesis of the search results:

• Text-Based Results:

  1. Methods for solving quadratic equations involving \( x^2 \).
  2. Step-by-step guides on solving equations of the form \( ax^2 + bx + c = 0 \).
  3. Algebraic approaches to finding roots of quadratic expressions.

• Video Results:

  1. Tutorials demonstrating how to solve \( x^2 \) equations visually.
  2. Educational videos explaining quadratic formula application.

• Image Results:

  1. Visual representations and graphs related to quadratic equations.
  2. Illustrative examples of solving \( x^2 \) equations graphically.

1. Introduction to x squared equations

2. Understanding the basics of x squared

3. Solving simple x squared equations

4. Advanced methods for solving x squared equations

5. Using the quadratic formula for x squared

6. Factoring techniques for x squared equations

7. Completing the square with x squared equations

8. Real-life applications of x squared in mathematics and beyond

9. Common mistakes to avoid when solving x squared

10. Practical tips and strategies for mastering x squared equations

X squared, denoted as \( x^2 \), represents the square of a variable x in algebra. It is a fundamental concept in quadratic equations and mathematical modeling, where it often describes relationships involving squares of quantities. Understanding x squared involves grasping its geometric interpretation as an area of a square with side length x, as well as its role in higher-level algebraic expressions and equations.

Solving x squared equations involves various methods depending on the complexity of the equation. Below are the general steps:

1. Identify the form of the equation: \( ax^2 + bx + c = 0 \).

2. Factor the equation if possible.

3. Use the quadratic formula: \( x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \).

4. Complete the square to find solutions.

5. Check solutions for accuracy by substituting back into the original equation.

There are several effective methods for solving equations involving x squared. Here are the detailed steps:

1. Factoring: Rewrite the equation in the form \( ax^2 + bx + c = 0 \) and factorize it into \( (px + q)(rx + s) = 0 \).

2. Completing the Square: Convert the equation to vertex form by adding and subtracting \( \left(\frac{b}{2}\right)^2 \).

3. Quadratic Formula: Use the formula \( x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \) to find the roots directly.

4. Graphical Methods: Plot the equation and find the x-intercepts where \( y = 0 \).

5. Numerical Methods: Use iterative techniques like Newton's method to approximate solutions.

Quadratic equations, which often involve solving for x squared, are used in various real-life scenarios. Here are some notable applications:

1. Architecture and Construction

Architects and builders use quadratic equations to calculate areas, volumes, and material requirements. For example, when designing a building, they might need to determine the optimal dimensions of rooms or the amount of materials needed for construction.

• Area Calculation: When planning the layout of a house, the total area of the building and individual rooms can be calculated using quadratic equations.
• Structural Design: Engineers use these equations to ensure the stability and integrity of structures, particularly in designing elements like arches and bridges.

2. Business and Economics

Quadratic equations help businesses determine profit maximization and cost minimization.

• Profit Analysis: Businesses use quadratic equations to calculate the maximum profit by finding the optimal price and production levels. For instance, the equation can help determine the price at which revenue equals cost, leading to maximum profit.
• Cost Management: Companies use these equations to analyze cost functions and minimize production costs while maintaining quality.

3. Physics and Engineering

In physics and engineering, quadratic equations are essential for solving problems related to motion, forces, and energy.

• Projectile Motion: The path of an object thrown into the air follows a parabolic trajectory, which can be described by a quadratic equation. This is useful in sports, engineering, and even video game design.
• Design and Manufacturing: Engineers use quadratic equations to design components and systems, such as calculating the stresses and strains on materials.

4. Astronomy and Space Exploration

Astronomers use quadratic equations to model the orbits of planets and other celestial bodies.

• Orbital Mechanics: The equations help in predicting the positions of planets and satellites, which is crucial for space missions and satellite communications.

5. Agriculture

Farmers and agricultural planners use quadratic equations to optimize the use of land and resources.

• Field Layout: Determining the optimal layout of fields and the amount of fertilizer or water needed can be calculated using quadratic equations.

6. Everyday Problem Solving

Quadratic equations appear in many everyday situations, such as calculating the area of a plot of land, optimizing storage solutions, and even in crafting and quilting.

• Crafting: When adding borders to quilts or other fabric projects, calculating the dimensions often involves solving quadratic equations to ensure the correct fit.

When solving equations involving \(x^2\), students often make several common mistakes. Understanding these mistakes can help in avoiding them and ensuring correct solutions. Here are some frequent errors and tips to avoid them:

1. Incorrectly Squaring Both Sides of an Equation

When squaring both sides of an equation, it's important to correctly apply the squaring process to each side as a whole. For instance, given an equation \(1 + \sqrt{4x + 13} = 2x\), squaring it incorrectly can lead to errors. The correct method is:

(1 + \sqrt{4x + 13})^2 = (2x)^2

This expands to:

1 + 2\sqrt{4x + 13} + (4x + 13) = 4x^2

Incorrectly squaring individual terms can lead to extraneous solutions or incorrect results.

2. Misplacing Parentheses

Parentheses are crucial in ensuring that operations are performed correctly. For example, when squaring \(4x\), it should be written as \((4x)^2\), which equals \(16x^2\). Incorrectly writing it as \(4x^2\) would only square the \(x\), not the 4, leading to wrong answers:

Correct: (4x)^2 = 16x^2
Incorrect: 4x^2

3. Overlooking Extraneous Solutions

Squaring both sides of an equation can introduce extraneous solutions. Always check the solutions in the original equation to ensure they are valid. For example:

1 + \sqrt{4x + 13} = 2x
\endcode>

Upon solving, you might find \(x = 3\) and \(x = -1\). Substituting back into the original equation helps verify the correct solution. Here, \(x = 3\) checks out, but \(x = -1\) does not.

4. Misinterpreting the Square Root

When solving \(\sqrt{x^2} = x\), remember that the square root function yields both positive and negative values. For example:

\sqrt{x^2} = |x|

This means \(\sqrt{25} = \pm 5\).

5. Forgetting to Factor Completely

Ensure to factor equations completely to find all possible solutions. For instance, solving \(x^2 - 5x + 6 = 0\) requires factoring to \((x - 2)(x - 3) = 0\), giving solutions \(x = 2\) and \(x = 3\).

6. Incorrectly Applying the Quadratic Formula

When using the quadratic formula \(\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), it's crucial to substitute values correctly and simplify properly. Errors in calculation or sign can lead to incorrect solutions.

By being aware of these common mistakes and taking care to avoid them, you can improve your accuracy in solving \(x^2\) equations.

Solving for \( x^2 \) can be straightforward if approached systematically. Here are some tips to enhance your effectiveness:

1. Understand the Problem: Ensure you clearly understand the equation and identify it as a quadratic equation of the form \( ax^2 + bx + c = 0 \).
2. Check for Factorization:

   Factorizing the quadratic equation is often the simplest method. Look for two numbers that multiply to give the constant term \( c \) and add to give the coefficient \( b \). For example:

   • For \( x^2 + 6x + 9 = 0 \), the factors of 9 that add up to 6 are 3 and 3.
   • Thus, the equation can be written as \( (x + 3)(x + 3) = 0 \).
3. Complete the Square:

   If factorization is not easy, use the completing the square method. This involves converting the equation into a perfect square trinomial. For example:

   • Rewrite \( x^2 + 8x + 15 = 0 \) as \( x^2 + 8x = -15 \).
   • Add and subtract \( (8/2)^2 = 16 \) to get \( x^2 + 8x + 16 = 1 \).
   • Thus, \( (x + 4)^2 = 1 \), giving solutions \( x = -3 \) and \( x = -5 \).
4. Use the Quadratic Formula:

   If the equation does not factorize easily and completing the square is cumbersome, use the quadratic formula:

   \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

   Apply this formula directly to find the roots of any quadratic equation.

5. Check Your Work:

   Always substitute your solutions back into the original equation to verify their correctness. This step ensures you haven't made any arithmetic errors.

6. Practice Regularly:

   Solving various types of quadratic equations helps improve your skill and speed. Regular practice is essential for mastery.

By following these tips, you can effectively solve quadratic equations and avoid common pitfalls.