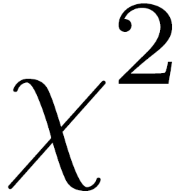Topic x squared x squared: Exploring the concept of "x squared x squared," this article delves into various mathematical operations involving squared terms. Learn how to simplify expressions, understand exponents, and solve equations effectively. Perfect for students and enthusiasts aiming to deepen their algebraic knowledge and problem-solving skills.
Table of Content
- Understanding X Squared
- Introduction to X Squared
- Basic Concept of Squaring a Number
- Mathematical Notation and Representation
- Understanding X Squared in Algebra
- Calculations Involving X Squared
- X Squared in Quadratic Equations
- Common Misconceptions about X Squared
- Practical Applications of X Squared
- Frequently Asked Questions
- YOUTUBE: Xem video để học cách giải phương trình x bình phương = 4 và khám phá các giá trị khác của x khi bình phương.
Understanding X Squared
The concept of "x squared" is fundamental in mathematics. It involves multiplying a number or variable, x, by itself, represented as \(x^2\). This operation forms the basis of quadratic equations and plays a significant role in various areas of math, from algebra to calculus.
Basic Concepts
- Definition: x squared ( \(x^2\) ) is the product of x multiplied by itself.
- Example: If \(x = 3\), then \(x^2 = 3 \times 3 = 9\).
- Application: Quadratic equations, which take the form \(ax^2 + bx + c = 0\), are used to solve many practical problems in physics and engineering.
Operations Involving X Squared
| Operation | Expression | Result |
|---|---|---|
| Adding x squared | \(x^2 + x^2\) | \(2x^2\) |
| Multiplying x squared | \(x^2 \times x^2\) | \(x^4\) |
Common Questions
- What is x squared? It is \(x \times x\), often written as \(x^2\).
- Why is it important? Understanding \(x^2\) is crucial for solving quadratic equations and understanding the properties of parabolas.
- Can x squared be negative? No, \(x^2\) is always non-negative if x is a real number. However, in the realm of complex numbers, it can be part of an expression that includes imaginary numbers.
Practical Examples
- If \(x^2 = 16\), find the value of x.
- Solve the equation \(x^2 = 9\).
- Solve for x in the equation \(3x^2 - 6 = 0\).
Understanding and working with \(x^2\) is a fundamental step in exploring more advanced mathematical concepts and their real-world applications.
For more detailed explanations and practice problems, you can visit educational resources such as Cuemath and Wolfram MathWorld.

READ MORE:
Introduction to X Squared
The concept of x squared is fundamental in mathematics, representing a number or variable multiplied by itself. Mathematically, this is written as \(x^2\). For instance, if \(x = 3\), then \(x^2 = 3 \times 3 = 9\). This basic operation is a building block for more advanced mathematical concepts and equations.
When dealing with algebra, \(x^2\) frequently appears in various types of equations, from simple to complex. Here are some essential points about \(x^2\):
- Simple Equations: An example of a simple equation involving \(x^2\) is \(x^2 = 4\), where the solutions are \(x = 2\) or \(x = -2\).
- Complex Equations: More complex equations, such as \(2x^2 - 5x + 2 = 0\), require the use of the quadratic formula to solve.
Understanding \(x^2\) is crucial for solving quadratic equations, which are expressed in the form \(ax^2 + bx + c = 0\). These equations are foundational in algebra and have numerous applications in various fields of study, including physics and engineering.
Here’s a step-by-step breakdown of how \(x^2\) functions in different scenarios:
- Multiplication of \(x^2\): When \(x^2\) is multiplied by itself, it is expressed as \(x^2 \times x^2 = x^4\). This follows the exponent rule where \(x^m \times x^n = x^{m+n}\).
- Adding \(x^2\): Adding two \(x^2\) terms results in \(x^2 + x^2 = 2x^2\), which simplifies the expression.
- Equations involving \(x^2\): In quadratic equations like \(ax^2 + bx + c = 0\), \(x^2\) determines the shape of the graph, typically a parabola.
Practicing the manipulation of \(x^2\) through various exercises can significantly enhance one’s mathematical skills. Here are some practice problems categorized by difficulty:
- Easy: Solve \(x^2 = 16\).
- Intermediate: Solve \(4x^2 = 36\).
- Hard: Solve the quadratic equation \(2x^2 - 5x + 3 = 0\).
In conclusion, mastering the concept of \(x^2\) is essential for progressing in mathematics. It not only forms the basis for more complex topics but also enhances problem-solving skills across various applications.
Basic Concept of Squaring a Number
The concept of squaring a number is fundamental in mathematics. It involves multiplying a number by itself. The notation for squaring a number \(x\) is \(x^2\), which reads as "x squared". This operation is frequently used in algebra, geometry, and many other areas of math.
Here is a detailed explanation of the basic concept of squaring a number:
- Definition: Squaring a number means multiplying the number by itself. For example, if \(x = 5\), then \(x^2 = 5 \times 5 = 25\).
- Mathematical Notation: The square of a number \(x\) is written as \(x^2\). This can also be expressed in various ways such as \(x \times x\), \(x \cdot x\), or simply \(xx\).
- Properties:
- Any real number squared is non-negative, i.e., \(x^2 \geq 0\).
- The square of a negative number is positive, i.e., \((-x)^2 = x^2\).
- The square of zero is zero, i.e., \(0^2 = 0\).
Let's go through some examples:
- Example 1: If \(x = 3\), then \(x^2 = 3 \times 3 = 9\).
- Example 2: If \(x = -4\), then \((-4)^2 = (-4) \times (-4) = 16\).
Squaring numbers is used in various mathematical contexts such as:
- Quadratic Equations: In a quadratic equation of the form \(ax^2 + bx + c = 0\), the term \(x^2\) plays a crucial role in determining the shape of the graph, which is a parabola.
- Area Calculations: The area of a square with side length \(x\) is given by \(x^2\).
- Pythagorean Theorem: In the context of right-angled triangles, the square of the hypotenuse is equal to the sum of the squares of the other two sides, i.e., \(c^2 = a^2 + b^2\).
Mathematical Notation and Representation
The concept of squaring a number is fundamental in mathematics. Squaring a number means multiplying the number by itself. This operation is represented mathematically as \( x^2 \), where \( x \) is any real or complex number.
The notation \( x^2 \) can be understood as follows:
- The base \( x \) is the number being squared.
- The exponent 2 indicates that the base is used as a factor twice.
This can be expressed in various mathematical contexts:
- Arithmetic: For any real number \( x \), squaring it results in \( x \cdot x \). For example, if \( x = 3 \), then \( x^2 = 3 \cdot 3 = 9 \).
- Geometry: Squaring is often used to calculate the area of a square. If the side length of a square is \( x \), then its area is \( x^2 \).
- Algebra: In algebra, \( x^2 \) is a common term in quadratic equations of the form \( ax^2 + bx + c = 0 \). Solving these equations often requires factoring or using the quadratic formula.
Here is a simple table showing different representations of squaring in various mathematical contexts:
| Context | Expression | Result |
|---|---|---|
| Arithmetic | \( x = 5 \) | \( x^2 = 25 \) |
| Geometry | Side length \( = 4 \) | Area \( = 16 \) |
| Algebra | \( 2x^2 - 3x + 1 = 0 \) | Solutions: \( x = 1 \) or \( x = \frac{1}{2} \) |
Understanding the notation and representation of \( x^2 \) is crucial for solving complex mathematical problems and for applications in various fields of science and engineering.
Understanding X Squared in Algebra
In algebra, the term "x squared" refers to the expression \(x^2\), which denotes a variable \(x\) being multiplied by itself. This fundamental concept is essential in various mathematical operations and equations, particularly in quadratic equations. Understanding how to manipulate and solve for \(x^2\) is crucial for progressing in algebra and other advanced mathematical fields.
Here is a detailed step-by-step explanation of \(x^2\) in algebra:
- Definition: \(x^2\) means \(x \times x\). For example, if \(x = 3\), then \(x^2 = 3 \times 3 = 9\).
- Properties:
- \(x^2\) is always non-negative for real numbers, as the product of a number with itself cannot be negative.
- \(x^2\) forms the basis of quadratic equations, which are polynomials of degree 2.
- Quadratic Equations:
- A quadratic equation is typically written in the form \(ax^2 + bx + c = 0\), where \(a\), \(b\), and \(c\) are constants.
- To solve quadratic equations, various methods such as factoring, completing the square, or using the quadratic formula \(\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) are employed.
- Graphical Representation:
- The graph of \(y = x^2\) is a parabola opening upwards, with its vertex at the origin (0,0).
- Quadratic equations can be visualized as parabolas, which helps in understanding the roots or solutions of the equation.
Understanding the concept of \(x^2\) and its applications in algebra is foundational for further studies in mathematics, including calculus and advanced algebraic theories. Practicing problems involving \(x^2\) and quadratic equations helps in developing a strong mathematical intuition and problem-solving skills.

Calculations Involving X Squared
Understanding and performing calculations involving x squared is fundamental in algebra and higher mathematics. Below is a detailed explanation and step-by-step process of handling such calculations.
- Simple Calculations: The simplest calculation involving x squared is to find the value of x when x squared is given. For example, if \(x^2 = 16\), then \(x\) can be either 4 or -4.
- Multiplying X Squared: When multiplying x squared by itself, the calculation follows the rule of exponents. For example:
\[
x^2 \times x^2 = x^{2+2} = x^4
\] - Quadratic Equations: A more complex application involves solving quadratic equations where x squared is a component. For example, solving \(2x^2 - 5x + 2 = 0\) requires the quadratic formula:
where \(a = 2\), \(b = -5\), and \(c = 2\).
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\] - Practice Problems:
- Easy: Solve \(x^2 = 9\). Here, \(x\) can be either 3 or -3.
- Intermediate: Solve \(4x^2 = 36\). Dividing both sides by 4, we get \(x^2 = 9\), so \(x\) is 3 or -3.
- Hard: Solve the quadratic equation \(2x^2 - 5x + 3 = 0\) using the quadratic formula.
By mastering these steps and practicing regularly, students can develop a strong understanding of calculations involving x squared, paving the way for success in more advanced mathematical concepts.
X Squared in Quadratic Equations
Understanding the role of x squared in quadratic equations is crucial for solving these mathematical problems. Quadratic equations are typically in the form \(ax^2 + bx + c = 0\), where \(x^2\) is the highest power of the variable. Let's delve into the details:
- Standard Form: The standard form of a quadratic equation is \(ax^2 + bx + c = 0\), where \(a \neq 0\). Here, \(a\), \(b\), and \(c\) are constants.
- Quadratic Formula: The solutions to the quadratic equation are found using the quadratic formula:
This formula provides the values of \(x\) that satisfy the equation.
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\] - Discriminant: The discriminant (\(b^2 - 4ac\)) determines the nature of the roots:
- If the discriminant is positive, there are two distinct real solutions.
- If it is zero, there is exactly one real solution.
- If it is negative, there are two complex solutions.
- Factoring: Some quadratic equations can be solved by factoring, where \(ax^2 + bx + c\) is expressed as a product of two binomials. For example:
\[
x^2 - 5x + 6 = (x - 2)(x - 3)
\] - Completing the Square: This method involves rewriting the quadratic equation in the form \((x - p)^2 = q\) to find the solutions. For instance:
\[
x^2 - 6x + 9 = (x - 3)^2
\] - Graphing: Quadratic equations can also be solved by graphing the parabola \(y = ax^2 + bx + c\) and identifying the points where the graph intersects the x-axis. These points are the solutions to the equation.
Understanding these various methods and the role of \(x^2\) in quadratic equations will enhance your ability to solve complex algebraic problems efficiently.
Common Misconceptions about X Squared
Understanding the concept of squaring a number can sometimes lead to misconceptions. Here are some common misconceptions about X squared:
-
Misconception 1: \( x^2 \) is always positive
While it is true that \( x^2 \) is non-negative for real numbers (i.e., \( x^2 \geq 0 \)), this does not imply that it is always positive. For example, if \( x = 0 \), then \( x^2 = 0 \).
-
Misconception 2: \( \sqrt{x^2} = x \)
This misconception arises from an incomplete understanding of the square root function. The correct expression should be \( \sqrt{x^2} = |x| \), where |x| denotes the absolute value of x. This means that \( \sqrt{x^2} \) is always non-negative, matching the definition of a square root.
-
Misconception 3: Squaring a number and doubling a number are the same
Squaring a number means multiplying it by itself, while doubling a number means multiplying it by two. For instance, \( 3^2 = 9 \) and \( 3 \times 2 = 6 \). These are clearly different operations.
-
Misconception 4: The square root of a number is always smaller than the original number
This is not always true. For numbers between 0 and 1, the square root is indeed larger than the original number. For example, \( \sqrt{0.25} = 0.5 \), which is greater than 0.25.
-
Misconception 5: \( x^2 \) and \( x \cdot 2 \) are equivalent
This is a misunderstanding of mathematical operations. Squaring a number results in \( x \times x \), whereas multiplying by 2 results in \( x \times 2 \). For example, \( 3^2 = 9 \) while \( 3 \times 2 = 6 \).
By addressing these misconceptions, students can develop a clearer and more accurate understanding of the properties of squaring a number and related mathematical concepts.
Practical Applications of X Squared
The concept of x squared (\(x^2\)) has numerous practical applications across various fields. Understanding these applications not only deepens our appreciation for this mathematical operation but also illustrates its significance in real-world scenarios.
- Physics and Engineering:
In physics, the formula \(x^2\) is often used to describe the area of square-shaped surfaces and the relationships in quadratic equations. For instance, when calculating the distance an object travels under constant acceleration, the equation \(s = ut + \frac{1}{2}at^2\) utilizes the squared term to account for acceleration.
Engineering problems often involve optimizing structures or materials, where quadratic equations help determine the most efficient dimensions and materials needed. For example, when designing a frame, the area calculations require solving quadratic equations to ensure optimal use of materials.
- Economics and Business:
Quadratic equations are essential in economics for modeling cost and revenue functions. For instance, a business might use a profit function represented by a quadratic equation \(P = -aP^2 + bP - c\) to determine the optimal price point for maximum profit.
In a practical scenario, suppose a company designs a new product and needs to maximize profit. By setting up and solving a quadratic equation that models their costs and revenues, they can find the price point that yields the highest profit.
- Sports and Games:
In sports, the trajectory of a ball is often modeled using quadratic equations. For example, the height of a ball thrown into the air can be described by \(h = -at^2 + bt + c\), where \(h\) is the height, \(t\) is the time, and \(a\), \(b\), and \(c\) are constants determined by the initial conditions of the throw.
- Architecture:
Architects use the principles of quadratic equations in designing parabolic structures, such as arches and bridges. These structures often need to support significant loads, and the parabolic shape, described mathematically by \(y = ax^2 + bx + c\), provides both strength and aesthetic appeal.
- Astronomy:
Quadratic equations are used in astronomy to calculate the orbits of celestial bodies. The position of planets and other objects in space can be predicted using formulas that involve squared terms, enabling accurate tracking and study of their movements.
Understanding and applying the concept of \(x^2\) is fundamental in solving various practical problems, making it a crucial component of both academic studies and real-world applications.

Frequently Asked Questions
-
What is X squared?
X squared, denoted as \( x^2 \), is a mathematical expression that refers to a number or variable \( x \) being multiplied by itself. For example, if \( x \) is 3, then \( x^2 \) would be \( 3 \times 3 = 9 \).
-
Why is X squared important in mathematics?
X squared is fundamental in many areas of mathematics. It forms the basis for quadratic equations, which are key in algebra and calculus. These equations help solve complex problems and model real-world situations such as projectile motion. In geometry, squaring is crucial for calculating areas of squares and rectangles.
-
How does X squared behave in an equation?
In a quadratic equation of the form \( ax^2 + bx + c = 0 \), \( x^2 \) determines the shape of the graph, which is a parabola. Whether \( x \) is positive or negative, \( x^2 \) always results in a non-negative value because the product of two negatives is positive. This can lead to equations with two solutions.
-
What is the difference between X and X squared?
'X' represents a number that hasn't been manipulated, while \( x^2 \) signifies that \( x \) is multiplied by itself. This difference impacts the graph of an equation: an equation with 'X' as its highest degree produces a straight line (linear equation), while one with \( x^2 \) produces a parabola (quadratic equation).
-
Can X squared be negative?
No, \( x^2 \) cannot be negative if \( x \) is a real number. The square of any real number, whether positive or negative, is always non-negative. However, in the realm of complex numbers, \( x \) can be an imaginary number, and \( x^2 \) can indeed be negative.
Xem video để học cách giải phương trình x bình phương = 4 và khám phá các giá trị khác của x khi bình phương.
Giải phương trình x bình phương = 4 và các giá trị bình phương khác của x
READ MORE:
Khám phá tất cả các nghiệm của phương trình x^2=2^x qua video này để hiểu rõ hơn về toán học và cách giải phương trình phức tạp.
Tất cả các nghiệm của phương trình x^2=2^x
:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)