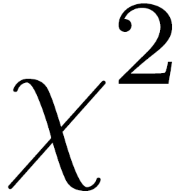Topic chi squared how to: Discover the essential guide on "Chi Squared How To" that will help you understand, calculate, and interpret the chi-squared test effectively. This comprehensive tutorial covers everything from basics to advanced topics, ensuring you gain confidence in applying this powerful statistical tool in various scenarios.
Table of Content
- Search Results for "chi squared how to"
- Introduction to Chi-Squared Test
- Understanding the Chi-Squared Distribution
- Types of Chi-Squared Tests
- Formulating Hypotheses for Chi-Squared Test
- Calculating Chi-Squared Test Statistic
- Degrees of Freedom in Chi-Squared Test
- Interpreting Chi-Squared Test Results
- Applications of Chi-Squared Test
- Chi-Squared Test Assumptions and Limitations
- Chi-Squared Test for Goodness of Fit
- Chi-Squared Test for Independence
- Chi-Squared Test for Homogeneity
- Examples and Practice Problems
- Using Chi-Squared Test in Statistical Software
- Common Mistakes in Chi-Squared Test
- Advanced Topics in Chi-Squared Test
- Frequently Asked Questions about Chi-Squared Test
- YOUTUBE: Video hướng dẫn kiểm định Chi-Square bằng tiếng Việt, giải thích chi tiết từng bước và các ứng dụng thực tiễn.
Search Results for "chi squared how to"
Here's a synthesis of the search results for the keyword "chi squared how to":
-
Statistical Analysis Guides
Many resources explain how to perform chi-squared tests for statistical analysis, outlining steps and formulas.
-
Video Tutorials
Several video tutorials demonstrate how to calculate and interpret chi-squared tests with practical examples.
-
Online Courses
Various online courses offer comprehensive lessons on chi-squared tests, suitable for learners at different levels.
-
Applications in Research
Guides on applying chi-squared tests in research, emphasizing proper methodology and interpretation of results.
:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)
READ MORE:
Introduction to Chi-Squared Test
The Chi-Squared Test is a statistical method used to determine if there is a significant association between categorical variables. It is widely applied in various fields including biology, social sciences, and business analytics.
Key aspects of the Chi-Squared Test include:
- Hypothesis Testing: It helps in testing hypotheses about the independence of variables or the goodness of fit of observed data to expected distributions.
- Types of Tests: There are different types of Chi-Squared tests such as tests for independence, goodness of fit, and homogeneity, each suited to different research questions.
- Calculation: The test statistic is calculated by comparing observed frequencies with expected frequencies under the null hypothesis.
- Degrees of Freedom: Degrees of freedom in the Chi-Squared test determine the number of independent values that can vary without violating any constraints.
- Interpretation: Results are interpreted based on the test statistic and p-value, where a low p-value suggests evidence against the null hypothesis.
Understanding the Chi-Squared Test is crucial for making informed decisions based on categorical data analysis.
Understanding the Chi-Squared Distribution
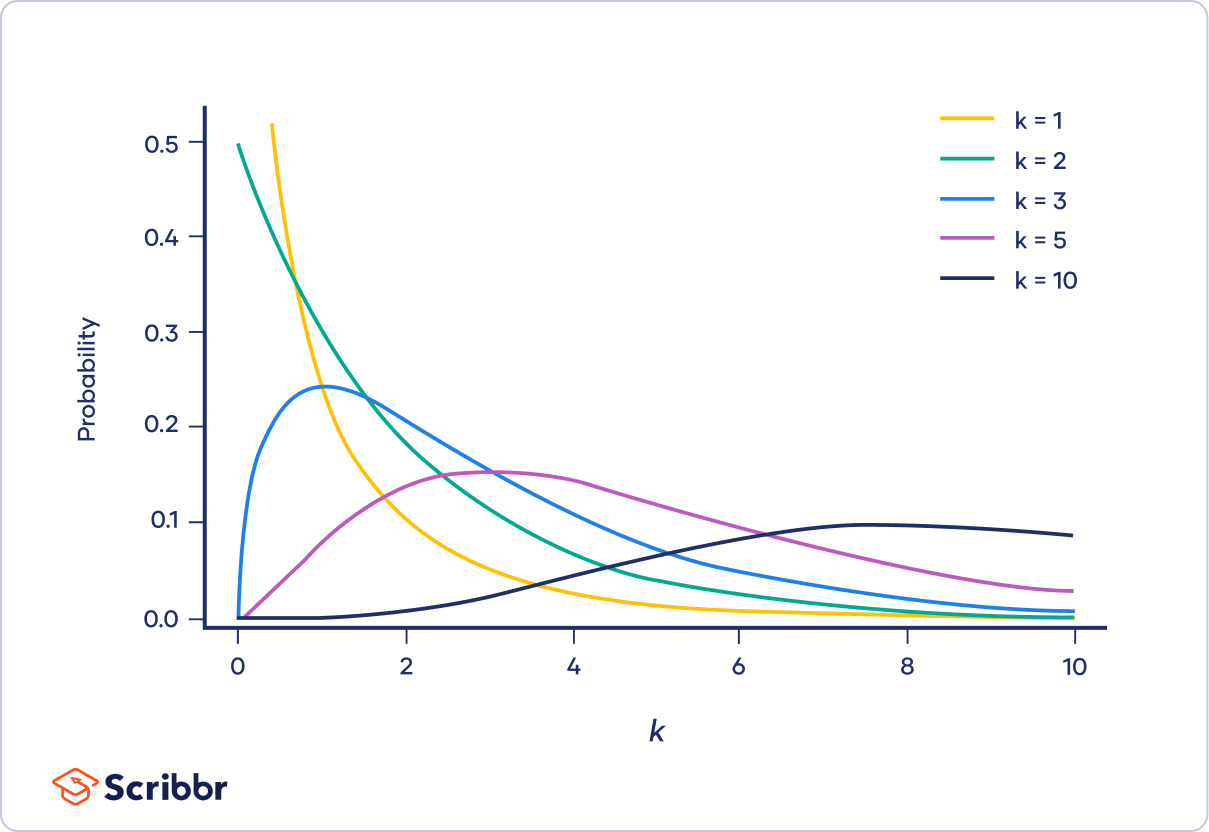
The Chi-Squared distribution is a probability distribution that arises in statistics, particularly in hypothesis testing and confidence interval estimation. It is characterized by its degrees of freedom, which dictate its shape.
Key points about the Chi-Squared distribution:
- Shape and Characteristics: It is positively skewed and its shape becomes more symmetric as the degrees of freedom increase.
- Application in Statistics: It is commonly used in Chi-Squared tests to assess the goodness of fit, test for independence in contingency tables, and analyze categorical data.
- Degrees of Freedom: The degrees of freedom parameter determines the variability of the distribution and is linked to the number of categories minus one in Chi-Squared tests.
- Properties: The Chi-Squared distribution is non-negative and its mean and variance increase with degrees of freedom.
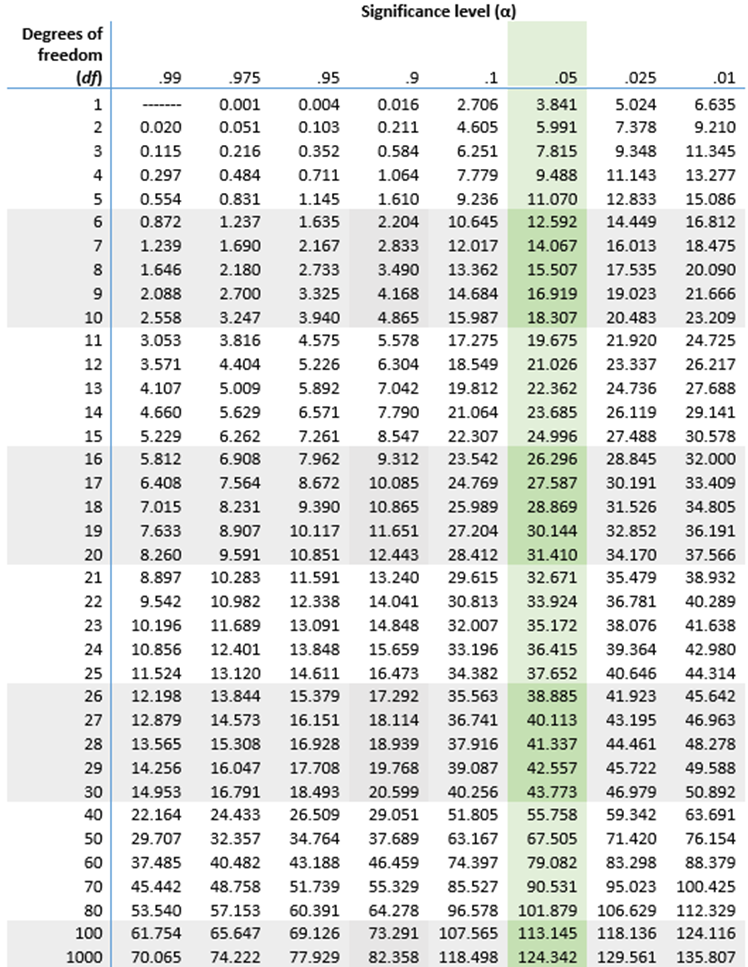
- Calculation: Probabilities related to the Chi-Squared distribution are often computed using statistical software or Chi-Squared tables, where critical values are compared to test statistics.
Understanding the Chi-Squared distribution is essential for accurately interpreting results in statistical analyses involving categorical data.
Types of Chi-Squared Tests
Chi-Squared tests are statistical procedures used to determine if there is a significant association between categorical variables. Different types of Chi-Squared tests include:
- Chi-Squared Test for Independence: This test examines whether there is a relationship between two categorical variables. It is commonly used in contingency tables to determine if the variables are independent or not.
- Chi-Squared Test for Goodness of Fit: This test evaluates how well an observed frequency distribution fits an expected theoretical distribution. It is useful for comparing observed data to a hypothesized distribution.
- Chi-Squared Test for Homogeneity: This test compares the distribution of a single categorical variable across different groups or populations. It determines if there are significant differences in the distribution patterns.
Each type of Chi-Squared test serves specific purposes in statistical analysis, helping researchers draw conclusions about relationships and distributions within categorical data.
Formulating Hypotheses for Chi-Squared Test
When conducting a Chi-Squared test, hypotheses are formulated to determine the relationship between categorical variables. The process involves:
- Null Hypothesis (H0): This hypothesis assumes that there is no significant relationship between the variables being tested. It suggests that any observed differences are due to random chance.
- Alternative Hypothesis (H1): This hypothesis proposes that there is a relationship or association between the variables beyond random chance. It suggests that the observed differences are statistically significant.
The formulation of hypotheses in a Chi-Squared test depends on the specific research question and the nature of the categorical variables being analyzed. Clear hypotheses are essential for interpreting the results and drawing meaningful conclusions from the statistical analysis.
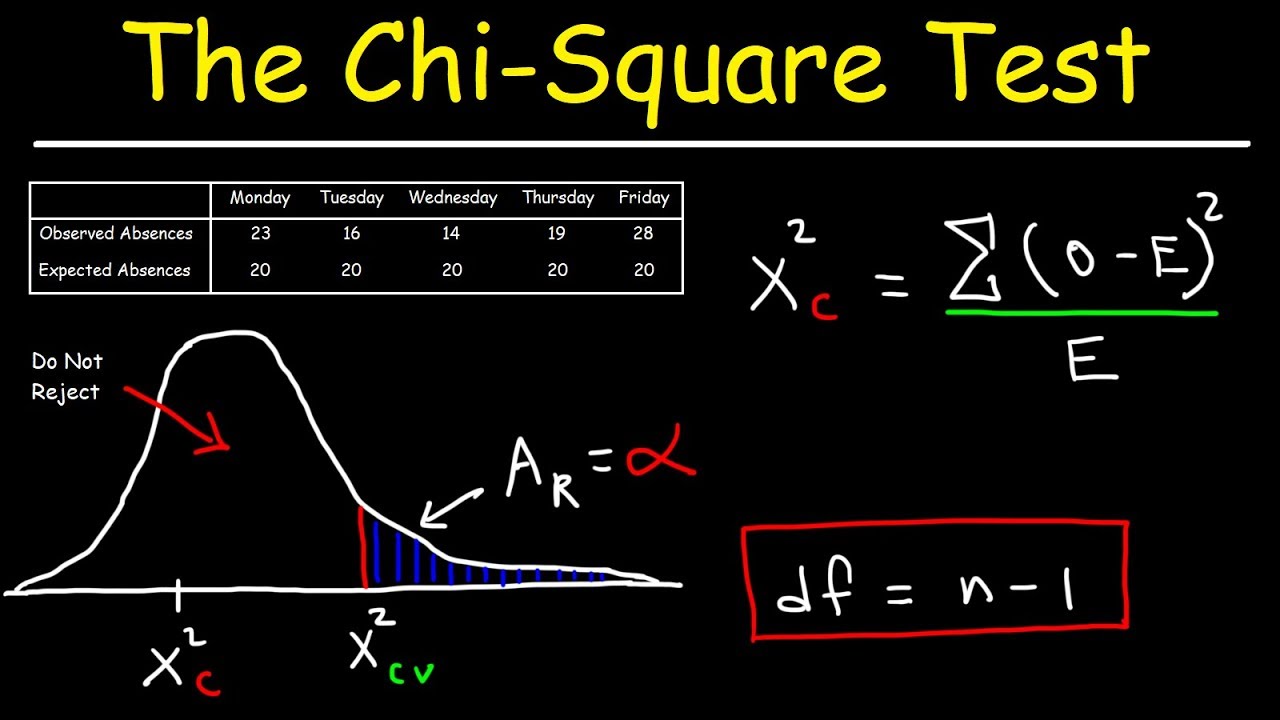
Calculating Chi-Squared Test Statistic
The Chi-Squared test statistic is computed to assess the significance of the relationship between categorical variables. Here's how it is calculated:
- Step 1: Setup Contingency Table: Construct a contingency table that summarizes the observed frequencies of the categorical variables.
- Step 2: Calculate Expected Frequencies: Compute the expected frequencies under the null hypothesis of independence or goodness of fit. This is typically done using formulas based on total counts and marginal proportions.
- Step 3: Compute Chi-Squared Statistic: Calculate the Chi-Squared statistic using the formula:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]
where \( O_i \) is the observed frequency and \( E_i \) is the expected frequency for each cell in the contingency table. - Step 4: Degrees of Freedom: Determine the degrees of freedom (df) based on the dimensions of the contingency table (number of rows and columns).
- Step 5: Interpretation: Compare the computed Chi-Squared value to critical values from the Chi-Squared distribution table or use statistical software to determine the p-value. A low p-value indicates strong evidence against the null hypothesis.
Calculating the Chi-Squared test statistic involves systematic steps to quantify the degree of association or goodness of fit between categorical variables in statistical analyses.
Degrees of Freedom in Chi-Squared Test
In the Chi-Squared test, degrees of freedom (df) determine the variability and constraints in the data analysis. Here’s how degrees of freedom are determined:
- Chi-Squared Test for Independence: For a Chi-Squared test assessing independence in a contingency table, degrees of freedom are calculated as \( (r - 1)(c - 1) \), where \( r \) is the number of rows and \( c \) is the number of columns in the table.
- Chi-Squared Test for Goodness of Fit: When testing goodness of fit, degrees of freedom are typically \( k - 1 \), where \( k \) is the number of categories or groups being compared.
- Chi-Squared Test for Homogeneity: For the homogeneity Chi-Squared test, degrees of freedom are determined based on the number of groups being compared.
Degrees of freedom play a crucial role in Chi-Squared tests by indicating the number of independent observations used to calculate the test statistic, influencing the interpretation of results and critical values.
Interpreting Chi-Squared Test Results
Interpreting Chi-Squared test results involves several key steps to draw meaningful conclusions:
- Calculate Chi-Squared Statistic: Compute the Chi-Squared statistic using observed and expected frequencies.
- Determine Degrees of Freedom: Find the degrees of freedom based on the dimensions of the contingency table.
- Consult Chi-Squared Distribution Table or Software: Compare the computed Chi-Squared value to critical values from the Chi-Squared distribution table or use statistical software to find the p-value.
- Assess Significance: If the calculated Chi-Squared value is greater than the critical value or if the p-value is less than the significance level (typically 0.05), reject the null hypothesis.
- Interpret Findings: Conclude whether there is a significant association between the categorical variables or if the data fits the expected distribution.
Interpreting Chi-Squared test results requires careful consideration of statistical significance and the implications for the research question or hypothesis being tested.
Applications of Chi-Squared Test
The Chi-Squared test is a versatile statistical tool used in various fields to analyze categorical data. Here are some key applications of the Chi-Squared test:
-
Goodness of Fit:
This test determines if a sample matches the expected distribution. For example, if a die is fair, each side should appear about the same number of times in a large number of rolls. The steps include:
- Define the null hypothesis (e.g., the die is fair).
- Collect data and count the frequency of each outcome.
- Calculate the expected frequencies under the null hypothesis.
- Use the Chi-Squared formula:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \] where \( O_i \) is the observed frequency and \( E_i \) is the expected frequency. - Compare the calculated \(\chi^2\) value with the critical value from the Chi-Squared distribution table.
- Decide to accept or reject the null hypothesis.
-
Test of Independence:
This test assesses whether two categorical variables are independent. For example, it can determine if there is an association between gender and voting preference. The steps include:
- Set up a contingency table with observed frequencies.
- Calculate the expected frequencies assuming independence:
\[ E_{ij} = \frac{(Row\ Total_i) \times (Column\ Total_j)}{Grand\ Total} \] - Use the Chi-Squared formula to compute the test statistic.
- Compare the test statistic to the critical value from the Chi-Squared distribution table.
- Make a decision regarding the null hypothesis.
-
Test of Homogeneity:
This test compares the distribution of a categorical variable across different populations. For example, it can compare the distribution of a survey response across different age groups. The procedure is similar to the test of independence:
- Create a contingency table for the observed frequencies in each group.
- Compute the expected frequencies assuming homogeneity.
- Calculate the Chi-Squared statistic using the formula.
- Compare the statistic to the critical value from the Chi-Squared distribution table.
- Determine whether to accept or reject the null hypothesis.
-
Genetics:
Chi-Squared tests are used in genetics to examine the inheritance patterns and test genetic hypotheses, such as the expected ratios of different genotypes or phenotypes in offspring.
-
Market Research:
In market research, Chi-Squared tests help in understanding consumer behavior, such as the preference for different product categories among different demographic groups.
-
Medical Research:
Chi-Squared tests are used to investigate the relationship between categorical variables, such as the association between a treatment and health outcomes in clinical trials.
Chi-Squared Test Assumptions and Limitations
The chi-squared test is a powerful statistical tool used to assess the goodness of fit and test for independence between categorical variables. However, like any statistical method, it comes with specific assumptions and limitations that must be considered to ensure valid results.
Assumptions
- Independence of Observations: Each observation in the dataset should be independent of the others. This means that the occurrence of one event should not influence the occurrence of another.
- Sample Size: The chi-squared test requires a sufficiently large sample size to ensure the validity of the approximation to the chi-squared distribution. A common rule of thumb is that each expected frequency should be at least 5.
- Categorical Data: The chi-squared test is designed for categorical data, not numerical or continuous data. The data should be in the form of counts or frequencies for categories.
- Expected Frequency: In a contingency table, the expected frequency for each cell should be calculated. These expected frequencies should ideally be 5 or more to maintain the validity of the test.
Limitations
- Sample Size Sensitivity: The chi-squared test can be sensitive to small sample sizes. When sample sizes are too small, the test might not have enough power to detect a significant effect.
- Approximation Accuracy: The chi-squared test relies on an approximation to the chi-squared distribution, which may not be accurate with small sample sizes or when expected frequencies are low.
- Non-Independence: The test assumes that the data points are independent. If there is any dependency among the observations, the results of the chi-squared test can be misleading.
- Only Categorical Data: The test cannot be used with continuous data or for testing relationships involving numerical variables without first converting them into categories, which may result in loss of information.
- Misleading Results: With large datasets, even small and practically insignificant differences can become statistically significant, leading to potentially misleading conclusions.
Steps to Check Assumptions and Address Limitations
- Ensure that data collection methods guarantee the independence of observations.
- Verify that the sample size is large enough and that expected frequencies in contingency tables meet the required threshold.
- Use alternative tests, such as Fisher’s Exact Test, if the sample size is too small for the chi-squared test.
- Consider the context and practical significance of the results, especially when dealing with large datasets, to avoid over-interpreting statistically significant findings.
By understanding and addressing these assumptions and limitations, researchers can more effectively utilize the chi-squared test to draw meaningful and accurate conclusions from their data.
Chi-Squared Test for Goodness of Fit
The Chi-Squared Test for Goodness of Fit is used to determine whether a sample data matches a population with a specific distribution. Here, we will outline the steps to perform this test and illustrate them with an example.
Steps to Perform the Chi-Squared Goodness of Fit Test
-
State the Hypotheses
Define the null and alternative hypotheses:- H0: The observed frequencies match the expected frequencies (data follows the hypothesized distribution).
- H1: The observed frequencies do not match the expected frequencies (data does not follow the hypothesized distribution).
-
Calculate the Test Statistic
Use the formula:
Where O represents the observed frequency and E represents the expected frequency.
-
Determine the Degrees of Freedom
Calculate the degrees of freedom using the formula:
Where n is the number of categories.
-
Compare the Test Statistic to the Critical Value
Find the critical value from the Chi-Squared distribution table based on the degrees of freedom and the chosen significance level (e.g., 0.05). If the test statistic exceeds the critical value, reject the null hypothesis.
Example
Consider a shop owner who claims that an equal number of customers visit his shop each weekday. An independent researcher records the number of customers over a week:
- Monday: 50 customers
- Tuesday: 60 customers
- Wednesday: 40 customers
- Thursday: 47 customers
- Friday: 53 customers
Total customers: 250. Expected customers per day: 50.
Calculate the Chi-Squared test statistic:
| Day | Observed (O) | Expected (E) | (O-E)2/E |
|---|---|---|---|
| Monday | 50 | 50 | 0 |
| Tuesday | 60 | 50 | 2 |
| Wednesday | 40 | 50 | 2 |
| Thursday | 47 | 50 | 0.18 |
| Friday | 53 | 50 | 0.18 |
| Total | 4.36 | ||
The test statistic is 4.36. With 4 degrees of freedom and a significance level of 0.05, the critical value is approximately 9.488. Since 4.36 < 9.488, we fail to reject the null hypothesis, indicating no significant difference between the observed and expected frequencies.
Chi-Squared Test for Independence
The Chi-Squared Test for Independence is used to determine if there is a significant association between two categorical variables. Here is a detailed guide on how to perform this test:
1. State the Hypotheses
- Null Hypothesis (\(H_0\)): The two variables are independent (no association).
- Alternative Hypothesis (\(H_a\)): The two variables are not independent (there is an association).
2. Formulate an Analysis Plan
- Significance Level: Choose a significance level (\(\alpha\)), often 0.05.
- Test Method: Use the Chi-Squared Test for Independence.
3. Collect and Organize the Data
Organize the data into a contingency table, showing the frequency of occurrences for each combination of the categorical variables.
4. Calculate the Expected Frequencies
For each cell in the contingency table, calculate the expected frequency using the formula:
\[ E_{r,c} = \frac{(n_{r} \cdot n_{c})}{n} \]
where \( E_{r,c} \) is the expected frequency for row \( r \) and column \( c \), \( n_{r} \) is the total number of observations in row \( r \), \( n_{c} \) is the total number of observations in column \( c \), and \( n \) is the total sample size.
5. Compute the Test Statistic
The test statistic for the Chi-Squared Test is calculated using:
\[ \chi^2 = \sum \frac{(O_{r,c} - E_{r,c})^2}{E_{r,c}} \]
where \( O_{r,c} \) is the observed frequency for row \( r \) and column \( c \), and \( E_{r,c} \) is the expected frequency.
6. Determine the Degrees of Freedom
The degrees of freedom (\( df \)) for the test are calculated as:
\[ df = (r - 1) \times (c - 1) \]
where \( r \) is the number of rows and \( c \) is the number of columns in the contingency table.
7. Find the P-Value
Using the chi-squared distribution with the calculated degrees of freedom, find the p-value associated with the test statistic.
8. Make a Decision
- If the p-value is less than or equal to the significance level (\(\alpha\)), reject the null hypothesis (\(H_0\)).
- If the p-value is greater than the significance level (\(\alpha\)), fail to reject the null hypothesis (\(H_0\)).
9. Interpret the Results
If the null hypothesis is rejected, conclude that there is a significant association between the two variables. If the null hypothesis is not rejected, conclude that there is not enough evidence to suggest an association between the variables.
Example
Consider an example where we want to test if there is an association between gender (male/female) and voting preference (Democrat/Republican/Independent). Suppose we collect data and organize it into the following contingency table:
| Democrat | Republican | Independent | Total | |
|---|---|---|---|---|
| Male | 20 | 30 | 10 | 60 |
| Female | 25 | 35 | 20 | 80 |
| Total | 45 | 65 | 30 | 140 |
Using the steps outlined above, calculate the expected frequencies, the test statistic, degrees of freedom, and the p-value to determine if there is an association between gender and voting preference.
Chi-Squared Test for Homogeneity
The Chi-Squared Test for Homogeneity is used to determine if two or more populations have the same distribution of a categorical variable. This test is similar to the Chi-Squared Test for Independence but focuses on comparing different populations rather than assessing the relationship between variables.
Hypotheses
- Null Hypothesis (\(H_0\)): The distributions of the populations are the same.
- Alternative Hypothesis (\(H_a\)): The distributions of the populations are not the same.
Steps to Perform the Chi-Squared Test for Homogeneity
- Formulate the Hypotheses: Define the null and alternative hypotheses.
- Collect Data: Gather data from the different populations and organize it into a contingency table.
- Calculate Expected Frequencies: For each cell in the table, calculate the expected frequency using the formula:
\[
E_{ij} = \frac{(R_i \cdot C_j)}{N}
\]
where \(E_{ij}\) is the expected frequency for cell (i, j), \(R_i\) is the total for row i, \(C_j\) is the total for column j, and \(N\) is the grand total. - Compute the Chi-Squared Statistic: Use the formula:
\[
\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}
\]
where \(O_{ij}\) is the observed frequency and \(E_{ij}\) is the expected frequency. - Determine Degrees of Freedom: Calculate the degrees of freedom using:
\[
df = (r - 1) \times (c - 1)
\]
where \(r\) is the number of rows and \(c\) is the number of columns. - Find the Critical Value: Use the chi-squared distribution table to find the critical value at the desired significance level (\(\alpha\)) with the calculated degrees of freedom.
- Make a Decision: Compare the chi-squared statistic to the critical value:
- If \(\chi^2\) is greater than the critical value, reject the null hypothesis.
- If \(\chi^2\) is less than or equal to the critical value, do not reject the null hypothesis.
Example
Suppose we want to test if two different teaching methods result in the same distribution of grades among students. We collect data from two classes, each using a different teaching method, and organize it into a contingency table:
| Grades | Method A | Method B |
|---|---|---|
| A | 30 | 25 |
| B | 45 | 35 |
| C | 25 | 40 |
| D | 10 | 20 |
| F | 5 | 10 |
Following the steps outlined, we calculate the expected frequencies, the chi-squared statistic, and compare it to the critical value to determine if the teaching methods result in the same distribution of grades.
The Chi-Squared Test for Homogeneity is a powerful tool for comparing distributions across different populations, ensuring robust statistical analysis in various fields.

Examples and Practice Problems
The following section provides examples and practice problems for the Chi-Squared test, helping you understand its application in real-world scenarios.
Example 1: Chi-Squared Test for Goodness of Fit
Suppose a shop owner claims that the number of customers visiting his shop each weekday is evenly distributed. To test this hypothesis, the number of customers visiting the shop each day of the week is recorded:
- Monday: 50 customers
- Tuesday: 60 customers
- Wednesday: 40 customers
- Thursday: 47 customers
- Friday: 53 customers
We use a Chi-Squared Goodness of Fit test to determine if the observed distribution matches the expected equal distribution.
Steps:
- State the hypotheses:
- Null hypothesis (\(H_0\)): The number of customers each day is equally distributed.
- Alternative hypothesis (\(H_A\)): The number of customers each day is not equally distributed.
- Calculate the expected frequencies: If the distribution is equal, the expected frequency for each day is \( \frac{250}{5} = 50 \) customers.
- Compute the Chi-Squared statistic using the formula: \[ X^2 = \sum \frac{(O_i - E_i)^2}{E_i} \] where \(O_i\) is the observed frequency and \(E_i\) is the expected frequency.
- Find the critical value from the Chi-Squared distribution table with \(df = n - 1 = 5 - 1 = 4\) degrees of freedom.
- Compare the computed \(X^2\) value with the critical value to determine whether to reject \(H_0\).
Practice Problem 1:
Conduct a Chi-Squared Goodness of Fit test to see if a die is fair. Roll the die 60 times and record the following frequencies:
- 1: 8
- 2: 10
- 3: 9
- 4: 12
- 5: 11
- 6: 10
Follow the steps outlined in Example 1 to determine if the die is fair.
Example 2: Chi-Squared Test for Independence
A researcher wants to know if there is an association between gender and political party preference. A sample of 500 voters is surveyed with the following results:
| Republican | Democrat | Independent | Total | |
|---|---|---|---|---|
| Male | 120 | 90 | 40 | 250 |
| Female | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Steps:
- State the hypotheses:
- Null hypothesis (\(H_0\)): There is no association between gender and political party preference.
- Alternative hypothesis (\(H_A\)): There is an association between gender and political party preference.
- Calculate the expected frequencies for each cell in the table: \[ E_{ij} = \frac{(Row\ total) \times (Column\ total)}{Grand\ total} \]
- Compute the Chi-Squared statistic: \[ X^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \]
- Determine the degrees of freedom: \(df = (r-1)(c-1)\) where \(r\) is the number of rows and \(c\) is the number of columns.
- Compare the computed \(X^2\) value with the critical value to decide whether to reject \(H_0\).
Practice Problem 2:
A biologist records the number of different species of birds visiting a feeder. The observed counts are:
- Species A: 15
- Species B: 18
- Species C: 10
- Species D: 12
Conduct a Chi-Squared Goodness of Fit test to determine if the number of visits by each species follows the same distribution.
These examples and practice problems are designed to help you understand how to apply the Chi-Squared test in various scenarios. Practice solving these problems to reinforce your understanding.
Using Chi-Squared Test in Statistical Software
The Chi-Squared test can be efficiently performed using various statistical software such as Excel, SPSS, R, and Python. Here, we'll outline the steps to conduct a Chi-Squared test in Excel and R, two popular tools for data analysis.
Chi-Squared Test in Excel
- Organize Your Data:
Ensure your data is in a contingency table format, with observed frequencies for different categories.
Category 1 Category 2 Category 3 Group 1 Observed Value 1 Observed Value 2 Observed Value 3 Group 2 Observed Value 4 Observed Value 5 Observed Value 6 - Calculate Expected Frequencies:
Use the formula
=(Row Total * Column Total) / Grand Totalfor each cell to find the expected frequencies. - Apply the Chi-Squared Test:
Use Excel’s CHISQ.TEST function:
=CHISQ.TEST(observed_range, expected_range) - Interpret the Results:
The function returns the p-value, which you compare against your significance level (e.g., 0.05). If the p-value is less than the significance level, reject the null hypothesis.
Chi-Squared Test in R
- Prepare Your Data:
Create a matrix with observed frequencies.
observed <- matrix(c(50, 30, 20, 40, 10, 50), nrow=2, byrow=TRUE) - Perform the Test:
Use the
chisq.test()function:result <- chisq.test(observed) - View the Results:
Print the results to see the test statistic, degrees of freedom, and p-value:
print(result) - Interpret the Results:
As with Excel, compare the p-value to your significance level to determine if you reject the null hypothesis.
Tips for Accurate Results
- Ensure your data meets the assumptions of the Chi-Squared test, particularly that expected frequencies are at least 5 for most cells.
- Double-check your data ranges and inputs to avoid errors.
- Use the p-value in conjunction with other analyses for a comprehensive understanding of your data.
Common Mistakes in Chi-Squared Test
The Chi-Squared test is a powerful statistical tool, but there are common mistakes that can lead to incorrect conclusions. Understanding and avoiding these mistakes ensures accurate results.
- Using Percentages Instead of Frequencies:
The Chi-Squared test requires the use of raw frequencies rather than percentages. Using percentages can artificially inflate sample sizes and lead to incorrect conclusions.
Observed Frequencies Expected Frequencies Heads: 31 Heads: 25 Tails: 19 Tails: 25 In this example, using percentages instead of frequencies would distort the Chi-Squared value and the resulting p-value.
- Not Including All Categories:
All possible categories must be included in the analysis. Omitting a category can lead to incorrect Chi-Squared calculations and wrong conclusions.
Observed Frequencies Expected Frequencies Heads: 31 Heads: 25 Tails: 19 Tails: 25 Every trial must fit into a category, and all categories must be included to correctly compute the Chi-Squared value.
- Small Sample Sizes:
The Chi-Squared test is less reliable with small sample sizes. The expected frequency in each category should be at least 5 for the test to be valid.
- Categories Not Mutually Exclusive:
Each data point should fit into only one category. Overlapping categories can distort the results.
For example, having categories like "Single", "Married", "Divorced", and "Widowed" requires careful handling to ensure individuals fit into only one category.
- Misinterpretation of Results:
Correctly interpreting the Chi-Squared statistic and the p-value is crucial. A significant p-value indicates rejecting the null hypothesis, while a non-significant p-value indicates failing to reject it.
Avoiding these common mistakes helps in performing accurate Chi-Squared tests and making valid conclusions.
Advanced Topics in Chi-Squared Test
The Chi-Squared test, while fundamental, has several advanced applications and considerations that extend its utility in statistical analysis. These topics explore deeper aspects and specialized uses of the Chi-Squared test.
-
Chi-Squared Distribution and Non-Normality:
The Chi-Squared test assumes that the underlying data follows a normal distribution. However, in real-world scenarios, data might deviate from normality. Adjustments and transformations can be applied to the data to better meet the test's assumptions.
-
Combining Chi-Squared Variables:
If \(X_1\) and \(X_2\) are independent chi-squared variables with degrees of freedom \(k_1\) and \(k_2\), respectively, their sum \(X = X_1 + X_2\) follows a chi-squared distribution with \(k_1 + k_2\) degrees of freedom. This property is crucial in complex models where multiple chi-squared variables are analyzed together.
-
Goodness-of-Fit for Composite Hypotheses:
While the standard goodness-of-fit test assesses how well a sample matches a specified distribution, composite hypotheses involve more complex scenarios where parameters are estimated from the data. The test must account for the degrees of freedom used in parameter estimation.
-
Large Sample Sizes:
With large datasets, even minor deviations from the expected values can lead to significant chi-squared statistics, making it essential to interpret the results in the context of sample size. Adjustments like Yates' correction for continuity can be applied to mitigate this issue.
-
Chi-Squared in Model Fitting:
Chi-squared statistics are widely used in fitting models to data, particularly in fields like genetics and physics. The fit of the model can be assessed by comparing the observed data with model predictions, using chi-squared statistics to quantify the goodness of fit.
-
Bayesian Approaches:
Bayesian statistics offer an alternative to traditional chi-squared tests, incorporating prior information into the analysis. Bayesian methods can provide more nuanced insights, especially in cases with small sample sizes or complex models.
-
Adjustments for Multiple Comparisons:
When conducting multiple chi-squared tests, the risk of Type I errors increases. Techniques like the Bonferroni correction adjust the significance level to account for multiple comparisons, reducing the likelihood of false positives.
Exploring these advanced topics enhances the application of chi-squared tests, providing more robust and accurate statistical analyses in complex scenarios.

Frequently Asked Questions about Chi-Squared Test
The Chi-Squared test is a versatile statistical tool used in various fields. Here are some frequently asked questions and detailed answers about the Chi-Squared test.
What is a Chi-Squared Test?
The Chi-Squared test is a statistical method used to determine if there is a significant association between categorical variables. It compares the observed frequencies in a contingency table to the frequencies expected if the variables were independent.
When should I use a Chi-Squared Test?
The Chi-Squared test is used when you have categorical data and want to assess whether there is an association between the variables. Common applications include testing independence between two variables or assessing goodness of fit for a distribution.
How do I calculate the Chi-Squared Test statistic?
The Chi-Squared test statistic is calculated using the formula:
where \(O\) represents the observed frequency and \(E\) represents the expected frequency.
What are the assumptions of the Chi-Squared Test?
- Independence: The samples must be independent of each other.
- Expected Frequency: The expected frequency in each cell of the contingency table should be at least 5.
- Sample Size: The total sample size should be large enough, typically at least 20.
What are the degrees of freedom in a Chi-Squared Test?
The degrees of freedom for a Chi-Squared test are calculated based on the number of categories in the variables being tested. For a test of independence, it is calculated as:
where \(r\) is the number of rows and \(c\) is the number of columns in the contingency table.
How do I interpret the results of a Chi-Squared Test?
To interpret the Chi-Squared test results, compare the calculated test statistic to the critical value from the Chi-Squared distribution table. If the test statistic is greater than the critical value, you reject the null hypothesis and conclude that there is a significant association between the variables.
What are some common errors in performing a Chi-Squared Test?
- Using inappropriate data: Ensure the data is categorical and meets the assumptions.
- Ignoring small expected frequencies: Combine categories if expected frequencies are too low.
- Misinterpreting the results: Understand the context and limitations of the test.
Can I use Chi-Squared Test for small sample sizes?
Chi-Squared tests are generally not recommended for small sample sizes due to the assumption that expected frequencies should be at least 5. For small samples, consider using Fisher's Exact Test.
How do I perform a Chi-Squared Test in statistical software?
Most statistical software packages, such as R, SPSS, and Python's SciPy library, have built-in functions to perform Chi-Squared tests. You typically need to input the observed frequencies in a contingency table format and the software will calculate the test statistic and p-value.
Video hướng dẫn kiểm định Chi-Square bằng tiếng Việt, giải thích chi tiết từng bước và các ứng dụng thực tiễn.
Kiểm Định Chi-Square
READ MORE:
Hướng Dẫn... Thực Hiện Kiểm Định Chi-Square (Bằng Tay)