Topic x squared factored: Unlock the secrets of factoring x squared equations with our comprehensive guide. Learn the essential techniques for breaking down complex quadratic expressions into simpler factors. Whether you're a student or a math enthusiast, our step-by-step approach will make factoring quadratic equations clear and straightforward. Dive in and master the art of factoring today!
Table of Content
- Factoring Quadratic Equations
- Introduction to Factoring
- Basic Concepts in Factoring
- Factoring Quadratic Equations
- Perfect Square Trinomials
- Difference of Squares
- Advanced Factoring Techniques
- Factoring Calculators and Tools
- YOUTUBE: Xem video hướng dẫn cách phân tích nhanh một tam thức bậc hai bằng phương pháp x để giải quyết bài toán phức tạp.
Factoring Quadratic Equations
Factoring quadratic equations is a fundamental skill in algebra. The process involves expressing a quadratic equation in the form
Factoring Simple Quadratics
Consider the quadratic equation:
- Identify a pair of integers whose product is the constant term \( c \) (which is -8) and whose sum is the coefficient of the linear term \( b \) (which is -2).
- For this equation, the integers are -4 and 2 because
\( -4 \times 2 = -8 \) and\( -4 + 2 = -2 \) . - Write the equation in its factored form:
\( (x - 4)(x + 2) = 0 \) .
Setting each factor to zero gives the solutions:
Factoring Using the AC Method
Consider a more complex quadratic equation:
- Multiply the leading coefficient \( a \) (which is 1) and the constant term \( c \) (which is 24) to get 24.
- Find a pair of integers whose product is 24 and whose sum is -11. These integers are -3 and -8.
- Rewrite the middle term using these integers:
\( x^2 - 3x - 8x + 24 \) . - Factor by grouping:
\( x(x - 3) - 8(x - 3) = 0 \) . - Factor out the common binomial:
\( (x - 3)(x - 8) = 0 \) .
Setting each factor to zero gives the solutions:
Factoring Differences of Squares
The difference of squares formula is a useful tool for factoring specific types of quadratic expressions. For example:
- Recognize that this can be written as a difference of squares:
\( x^2 - 4^2 \) . - Apply the formula
\( a^2 - b^2 = (a + b)(a - b) \) : - Write the equation in its factored form:
\( (x + 4)(x - 4) = 0 \) .
Setting each factor to zero gives the solutions:
Using Factoring Calculators
Online factoring calculators, such as those provided by Mathway and Symbolab, can help you factor complex expressions step by step:
These tools allow you to input your quadratic equations and provide detailed steps to reach the factored form.
Factoring quadratics is a vital skill for solving algebraic equations, simplifying expressions, and understanding more advanced mathematical concepts. Practice and use of these methods will enhance your proficiency in algebra.

READ MORE:
Introduction to Factoring
Factoring is a fundamental mathematical process used to simplify expressions and solve equations. It involves breaking down a complex expression into a product of simpler factors. This process is crucial in algebra and is used to solve quadratic equations, simplify polynomial expressions, and find roots of equations.
Here are some key steps and methods involved in factoring:
- Identify the type of polynomial: Recognize whether you are dealing with a quadratic, cubic, or higher-degree polynomial.
- Find the Greatest Common Factor (GCF): Determine if there is a common factor in all terms of the polynomial and factor it out.
- Use special factoring formulas: Apply formulas such as the difference of squares, perfect square trinomials, and sum or difference of cubes.
- Factor by grouping: Group terms with common factors and factor them separately.
- Solve for the roots: Once the polynomial is factored, set each factor to zero and solve for the variable.
For example, to factor the quadratic expression \(x^2 - x - 12\), you look for two numbers that multiply to -12 and add to -1. These numbers are 3 and -4, so the factored form is \((x + 3)(x - 4)\).
Factoring is a powerful tool that simplifies solving equations and understanding the properties of polynomial functions.
Basic Concepts in Factoring
Factoring is a fundamental mathematical process used to break down complex expressions into simpler, more manageable components. This process is especially useful in solving equations and simplifying expressions. The primary goal of factoring is to rewrite an expression as a product of its factors.
Here are some key concepts in factoring:
- Greatest Common Factor (GCF): Identify the largest factor common to all terms in the expression and factor it out.
- Difference of Squares: Recognize patterns such as \(a^2 - b^2\), which can be factored into \((a - b)(a + b)\).
- Trinomials: Factor expressions of the form \(ax^2 + bx + c\). Look for two numbers that multiply to \(ac\) and add to \(b\).
- Perfect Square Trinomials: Identify expressions like \(a^2 + 2ab + b^2\) which factor into \((a + b)^2\).
- Grouping: For polynomials with four or more terms, group terms to find common factors and simplify.
Factoring requires practice and recognition of patterns. Here's a step-by-step example for factoring a simple quadratic expression:
- Consider the quadratic expression \(x^2 - 5x + 6\).
- Identify two numbers that multiply to 6 (the constant term) and add to -5 (the coefficient of the linear term). These numbers are -2 and -3.
- Rewrite the expression using these numbers: \(x^2 - 2x - 3x + 6\).
- Group the terms: \((x^2 - 2x) + (-3x + 6)\).
- Factor out the common factors: \(x(x - 2) - 3(x - 2)\).
- Factor out the common binomial: \((x - 3)(x - 2)\).
By following these steps, the expression \(x^2 - 5x + 6\) is factored into \((x - 3)(x - 2)\). Understanding these basic concepts and practicing different types of factoring will improve your ability to work with algebraic expressions efficiently.
Factoring Quadratic Equations
Factoring quadratic equations involves rewriting a quadratic expression in the form \(ax^2 + bx + c\) as a product of its linear factors. This process is essential for solving quadratic equations and understanding their properties.
Here are the steps to factor a quadratic equation:
- Identify the quadratic equation: Write the equation in the standard form \(ax^2 + bx + c = 0\).
- Find two numbers that multiply to \(ac\) (the product of the coefficient of \(x^2\) and the constant term) and add to \(b\) (the coefficient of \(x\)).
- Rewrite the middle term \(bx\) using the two numbers found: Split the middle term into two terms that add up to \(bx\).
- Group the terms: Group the terms into two pairs, each containing a common factor.
- Factor out the common factors from each group: Extract the common factor from each group to simplify the expression.
- Factor out the common binomial factor: Combine the groups to express the quadratic as a product of two binomials.
Let's see an example:
Consider the quadratic equation \(x^2 + 5x + 6\):
- Identify the equation: \(x^2 + 5x + 6\).
- Find two numbers that multiply to 6 (the constant term) and add to 5 (the coefficient of \(x\)). These numbers are 2 and 3.
- Rewrite the middle term: \(x^2 + 2x + 3x + 6\).
- Group the terms: \((x^2 + 2x) + (3x + 6)\).
- Factor out the common factors: \(x(x + 2) + 3(x + 2)\).
- Factor out the common binomial factor: \((x + 3)(x + 2)\).
The factored form of \(x^2 + 5x + 6\) is \((x + 3)(x + 2)\). Factoring quadratics is a powerful technique that simplifies solving equations and analyzing their roots.
Perfect Square Trinomials
A perfect square trinomial is a quadratic expression that can be factored into the square of a binomial. It takes the form:
\( ax^2 + bx + c \)
where \( a \), \( b \), and \( c \) are constants, and \( a \neq 0 \).
To factor a perfect square trinomial, follow these steps:
- Identify if the trinomial is a perfect square trinomial by checking if the first and last terms are perfect squares.
- Write the trinomial in the form \( (px + q)^2 \), where \( p \) and \( q \) are appropriate constants.
- Expand \( (px + q)^2 \) to verify that it equals the original trinomial.
Example:
Factor \( x^2 + 6x + 9 \):
We recognize \( x^2 + 6x + 9 \) as a perfect square trinomial because \( 9 \) is \( 3^2 \).
Factorization:
\( x^2 + 6x + 9 = (x + 3)^2 \)
Verification:
Expanding \( (x + 3)^2 \) gives us \( x^2 + 6x + 9 \), confirming our factorization is correct.

Difference of Squares
The difference of squares is a specific algebraic factorization pattern for expressions of the form:
\( a^2 - b^2 \)
where \( a \) and \( b \) are any algebraic expressions (could be constants, variables, or both).
To factor a difference of squares, use the following steps:
- Identify the expression as \( a^2 - b^2 \).
- Factorize using the formula:
- Verify the factorization by expanding \( (a - b)(a + b) \) to ensure it equals the original expression.
\( a^2 - b^2 = (a - b)(a + b) \)
Example:
Factor \( x^2 - 9 \):
We recognize \( x^2 - 9 \) as a difference of squares because \( x^2 \) is \( x^2 \) and \( 9 \) is \( 3^2 \).
Factorization:
\( x^2 - 9 = (x - 3)(x + 3) \)
Verification:
Expanding \( (x - 3)(x + 3) \) gives us \( x^2 - 9 \), confirming our factorization is correct.
Advanced Factoring Techniques
Advanced factoring techniques involve methods beyond basic quadratic factoring, addressing more complex scenarios and special cases.
Key techniques include:
- Factoring by Grouping: Used when a polynomial has four terms that can be grouped and factored.
- Factoring Trinomials with Leading Coefficients: Involves factoring trinomials where the leading coefficient \( a \) is not 1.
- Factoring by Substitution: Substituting variables to simplify factoring processes, especially useful for complex polynomials.
- Factoring Special Cases: Techniques for factoring special forms like sums and differences of cubes, higher-degree polynomials, and multivariable expressions.
These techniques are essential for solving advanced algebraic equations, simplifying expressions, and identifying polynomial roots efficiently.
Factoring Calculators and Tools
Factoring calculators and tools provide convenient ways to factorize quadratic and higher-degree polynomial expressions online. These tools typically offer:
- Automatic Factoring: Instantly factorizes entered polynomial expressions, saving time and effort.
- Step-by-Step Solutions: Some calculators provide detailed steps showing how the factorization was achieved.
- Graphical Representations: Visual aids such as graphs and diagrams to illustrate factorized forms.
- Variable Support: Capabilities to handle expressions with variables, allowing users to factorize algebraic equations.
- Additional Features: Some tools may include options to solve related equations, find roots, or simplify fractions.
These calculators are valuable for students, educators, and professionals needing quick and accurate solutions to complex polynomial factorization problems.
Xem video hướng dẫn cách phân tích nhanh một tam thức bậc hai bằng phương pháp x để giải quyết bài toán phức tạp.
Video nhanh chóng phân tích một tam thức bậc hai bằng phương pháp x
READ MORE:
Xem video hướng dẫn cách phân tích sử dụng hiệu của hai bình phương để giải quyết các bài toán liên quan đến đại số.
Phân Tích Sử Dụng Hiệu Của Hai Bình Phương

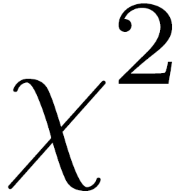






:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)