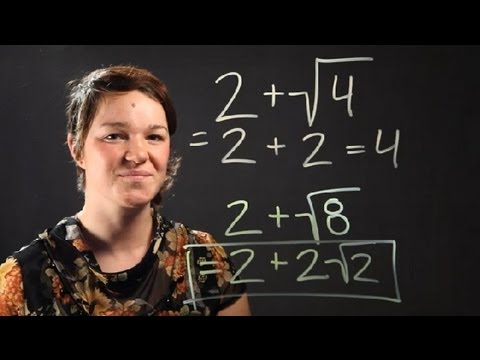How to Add or Subtract Square Roots: A Complete Guide for Beginners

Adding and subtracting square roots can be done by following specific rules and understanding the properties of square roots. Below are the detailed steps to add or subtract square roots.

1. Simplify the Square Roots

Before adding or subtracting square roots, simplify them as much as possible.

• Find the prime factorization of the number inside the square root.
• Pair the prime factors.
• Move pairs of factors outside the square root.

Example:

\(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)

2. Combine Like Terms

Like terms in square roots are those with the same radicand (the number inside the square root). Only like terms can be added or subtracted.

Example:

\(3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2}\)

For different radicands, they cannot be combined:

\(3\sqrt{2} + 4\sqrt{3} = 3\sqrt{2} + 4\sqrt{3}\) (cannot be simplified further)

3. Perform Addition or Subtraction

Once you have identified and simplified like terms, you can add or subtract them as you would with regular numbers.

1. Simplify each square root term.
2. Add or subtract the coefficients of the like terms.

Examples:

\(7\sqrt{5} - 3\sqrt{5} = (7 - 3)\sqrt{5} = 4\sqrt{5}\)

\(\sqrt{18} + \sqrt{50} = 3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2}\)

4. Practice Problems

• Simplify: \(\sqrt{12} + \sqrt{27}\)

Solution: \(\sqrt{12} = 2\sqrt{3}, \sqrt{27} = 3\sqrt{3} \Rightarrow 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\)

• Simplify: \(5\sqrt{8} - 2\sqrt{18}\)

Solution: \(5\sqrt{8} = 10\sqrt{2}, 2\sqrt{18} = 6\sqrt{2} \Rightarrow 10\sqrt{2} - 6\sqrt{2} = 4\sqrt{2}\)

By following these steps, you can effectively add and subtract square roots, ensuring you always simplify and combine like terms properly.

Square roots are mathematical operations that find the original number which, when multiplied by itself, produces a given number. For example, the square root of 16 is 4, because \(4 \times 4 = 16\). Understanding square roots is essential for various mathematical concepts and real-world applications.

The square root symbol is represented as \(\sqrt{}\). For instance, \(\sqrt{25} = 5\), since \(5 \times 5 = 25\).

Here are some fundamental properties of square roots:

• The square root of a number \(n\) is a value \(x\) such that \(x^2 = n\).
• Square roots of positive numbers are always non-negative.
• Every positive number has two square roots: one positive (principal square root) and one negative. For example, the square roots of 9 are 3 and -3.
• The square root of 0 is 0.
• Square roots of negative numbers are not real numbers; they are complex numbers.

Square roots are often simplified to make calculations easier. For example, \(\sqrt{18}\) can be simplified by factoring the radicand:

\(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)

Understanding these basic properties and simplification methods lays the foundation for more complex operations involving square roots, such as addition and subtraction.

Understanding the basic properties of square roots is essential for performing operations such as addition and subtraction. Here are the key properties of square roots:

• Non-Negative Output: The principal square root of a non-negative number is always non-negative. For example, \(\sqrt{25} = 5\), not -5.
• Product Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).

Example: \(\sqrt{36 \times 4} = \sqrt{36} \times \sqrt{4} = 6 \times 2 = 12\).

• Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. Mathematically, \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).

Example: \(\sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3}\).

• Squares of Square Roots: The square of a square root returns the original number. Mathematically, \((\sqrt{a})^2 = a\).

Example: \((\sqrt{5})^2 = 5\).

• Addition and Subtraction of Like Radicands: Square roots with the same radicand can be added or subtracted by combining their coefficients. For example, \(3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2}\).
• Simplifying Square Roots: Square roots can often be simplified by factoring out perfect squares from the radicand.

Example: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).

These properties provide the foundation for manipulating square roots in various mathematical contexts, making it easier to perform addition, subtraction, and other operations.

Simplifying square roots involves reducing the radicand (the number inside the square root) to its simplest form. Here are the steps to simplify square roots:

1. Find the Prime Factorization:

   Break down the radicand into its prime factors. This helps identify perfect squares within the radicand.

   • Example: For \(\sqrt{72}\), the prime factorization of 72 is \(2 \times 2 \times 2 \times 3 \times 3\).
2. Pair the Prime Factors:

   Group the prime factors into pairs of identical numbers.

   • Example: \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2}\).
3. Move Pairs Outside the Square Root:

   Each pair of identical factors can be moved outside the square root as a single factor.

   • Example: \(\sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
4. Multiply the Factors Outside the Square Root:

   Combine the factors outside the square root to get the simplified form.

   • Example: The simplified form of \(\sqrt{72}\) is \(6\sqrt{2}\).
5. Check for Further Simplification:

   Ensure that the radicand cannot be simplified further. If it can, repeat the steps above.

Let's look at another example:

Simplify \(\sqrt{200}\).

1. Prime factorization of 200: \(2 \times 2 \times 2 \times 5 \times 5\).
2. Pair the factors: \(\sqrt{(2 \times 2) \times (5 \times 5) \times 2}\).
3. Move pairs outside: \(2 \times 5 \times \sqrt{2} = 10\sqrt{2}\).
4. Simplified form: \(10\sqrt{2}\).

By following these steps, you can simplify any square root, making it easier to perform additional operations such as addition and subtraction.

Combining like terms in square roots involves adding or subtracting square roots that have the same radicand. Here are the steps to combine like terms in square roots:

1. Identify Like Terms:

   Like terms in square roots have the same radicand. Only these terms can be combined through addition or subtraction.

   • Example: \(3\sqrt{2}\) and \(5\sqrt{2}\) are like terms because they share the same radicand (\(\sqrt{2}\)).
   • \(3\sqrt{2}\) and \(4\sqrt{3}\) are not like terms because they have different radicands (\(\sqrt{2}\) and \(\sqrt{3}\)).
2. Add or Subtract the Coefficients:

   Once like terms are identified, add or subtract their coefficients while keeping the radicand the same.

   • Example: \(3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2}\).
   • Example: \(7\sqrt{3} - 2\sqrt{3} = (7 - 2)\sqrt{3} = 5\sqrt{3}\).
3. Simplify the Result:

   Ensure the resulting expression is in its simplest form.

Here are a few more examples:

Example 1: Combine \(4\sqrt{5} + 6\sqrt{5}\).

• Identify like terms: Both terms have the radicand \(\sqrt{5}\).
• Add the coefficients: \(4 + 6 = 10\).
• Result: \(4\sqrt{5} + 6\sqrt{5} = 10\sqrt{5}\).

Example 2: Combine \(9\sqrt{7} - 3\sqrt{7}\).

• Identify like terms: Both terms have the radicand \(\sqrt{7}\).
• Subtract the coefficients: \(9 - 3 = 6\).
• Result: \(9\sqrt{7} - 3\sqrt{7} = 6\sqrt{7}\).

Example 3: Combine \(2\sqrt{6} + 3\sqrt{2}\).

• Identify like terms: The terms have different radicands (\(\sqrt{6}\) and \(\sqrt{2}\)), so they cannot be combined.
• Result: \(2\sqrt{6} + 3\sqrt{2}\) (cannot be simplified further).

By following these steps, you can effectively combine like terms in square roots, ensuring accurate addition and subtraction of square root expressions.

Adding square roots involves combining terms with the same radicand. Here are the detailed steps to add square roots effectively:

1. Simplify Each Square Root:

   Before adding, simplify each square root if possible. This helps in identifying like terms more easily.

   • Example: \(\sqrt{50} + \sqrt{18}\)
   • Simplify: \(\sqrt{50} = 5\sqrt{2}\), \(\sqrt{18} = 3\sqrt{2}\)
2. Identify Like Terms:

   Check if the square roots have the same radicand. Only like terms can be combined.

   • Example: \(5\sqrt{2}\) and \(3\sqrt{2}\) are like terms because they share the same radicand (\(\sqrt{2}\)).
   • Example: \(5\sqrt{2}\) and \(4\sqrt{3}\) are not like terms because they have different radicands.
3. Add the Coefficients:

   Once like terms are identified, add their coefficients while keeping the radicand the same.

   • Example: \(5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2}\)
4. Combine and Simplify:

   If there are terms with different radicands, write them as separate terms in the final expression.

   • Example: \(4\sqrt{3} + 2\sqrt{5}\) cannot be simplified further and should be left as is.

Examples:

Example 1: Add \(\sqrt{12} + \sqrt{27}\)

1. Simplify: \(\sqrt{12} = 2\sqrt{3}\), \(\sqrt{27} = 3\sqrt{3}\)
2. Identify like terms: \(2\sqrt{3}\) and \(3\sqrt{3}\)
3. Add the coefficients: \(2 + 3 = 5\)
4. Result: \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\)

Example 2: Add \(2\sqrt{7} + 5\sqrt{7}\)

1. Identify like terms: \(2\sqrt{7}\) and \(5\sqrt{7}\)
2. Add the coefficients: \(2 + 5 = 7\)
3. Result: \(2\sqrt{7} + 5\sqrt{7} = 7\sqrt{7}\)

Example 3: Add \(3\sqrt{2} + 4\sqrt{3}\)

• Identify like terms: \(3\sqrt{2}\) and \(4\sqrt{3}\) are not like terms
• Result: \(3\sqrt{2} + 4\sqrt{3}\) (cannot be simplified further)

By following these methods, you can accurately add square roots, ensuring you combine only like terms and simplify where possible.

Subtracting square roots involves combining terms with the same radicand. Here are the detailed steps to subtract square roots effectively:

1. Simplify Each Square Root:

   Before subtracting, simplify each square root if possible. This helps in identifying like terms more easily.

   • Example: \(\sqrt{50} - \sqrt{18}\)
   • Simplify: \(\sqrt{50} = 5\sqrt{2}\), \(\sqrt{18} = 3\sqrt{2}\)
2. Identify Like Terms:

   Check if the square roots have the same radicand. Only like terms can be combined.

   • Example: \(5\sqrt{2}\) and \(3\sqrt{2}\) are like terms because they share the same radicand (\(\sqrt{2}\)).
   • Example: \(5\sqrt{2}\) and \(4\sqrt{3}\) are not like terms because they have different radicands.
3. Subtract the Coefficients:

   Once like terms are identified, subtract their coefficients while keeping the radicand the same.

   • Example: \(5\sqrt{2} - 3\sqrt{2} = (5 - 3)\sqrt{2} = 2\sqrt{2}\)
4. Combine and Simplify:

   If there are terms with different radicands, write them as separate terms in the final expression.

   • Example: \(4\sqrt{3} - 2\sqrt{5}\) cannot be simplified further and should be left as is.

Examples:

Example 1: Subtract \(\sqrt{32} - \sqrt{8}\)

1. Simplify: \(\sqrt{32} = 4\sqrt{2}\), \(\sqrt{8} = 2\sqrt{2}\)
2. Identify like terms: \(4\sqrt{2}\) and \(2\sqrt{2}\)
3. Subtract the coefficients: \(4 - 2 = 2\)
4. Result: \(4\sqrt{2} - 2\sqrt{2} = 2\sqrt{2}\)

Example 2: Subtract \(7\sqrt{5} - 3\sqrt{5}\)

1. Identify like terms: \(7\sqrt{5}\) and \(3\sqrt{5}\)
2. Subtract the coefficients: \(7 - 3 = 4\)
3. Result: \(7\sqrt{5} - 3\sqrt{5} = 4\sqrt{5}\)

Example 3: Subtract \(6\sqrt{2} - 2\sqrt{3}\)

• Identify like terms: \(6\sqrt{2}\) and \(2\sqrt{3}\) are not like terms
• Result: \(6\sqrt{2} - 2\sqrt{3}\) (cannot be simplified further)

By following these methods, you can accurately subtract square roots, ensuring you combine only like terms and simplify where possible.

When adding and subtracting square roots, certain special cases may arise. Understanding these special cases can help simplify the process and ensure accurate calculations. Here are some key special cases to consider:

1. Square Roots of Perfect Squares:

   If the square root involves perfect squares, simplify them to their integer values before performing addition or subtraction.

   • Example: \(\sqrt{16} + \sqrt{25} = 4 + 5 = 9\)
   • Example: \(\sqrt{36} - \sqrt{9} = 6 - 3 = 3\)
2. Combining Different Radicands:

   Square roots with different radicands cannot be directly added or subtracted. However, if the radicands can be simplified to a common form, then combining them is possible.

   • Example: \(\sqrt{50} + \sqrt{18} = 5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}\)
3. Square Roots Involving Variables:

   When dealing with square roots of variables, apply the same rules as for numerical values. Ensure the variables are like terms before combining them.

   • Example: \(\sqrt{a^2b} + \sqrt{ab^2} = a\sqrt{b} + b\sqrt{a}\) (cannot be simplified further)
4. Combining Rational and Irrational Terms:

   Rational numbers (integers or fractions) can sometimes combine with irrational square roots through multiplication or distribution, but they cannot be added directly.

   • Example: \(3 + 2\sqrt{5}\) (cannot be simplified further)
   • Example: \(2\sqrt{3} + 4\sqrt{3} = (2 + 4)\sqrt{3} = 6\sqrt{3}\)
5. Nested Square Roots:

   For expressions involving nested square roots, simplify the innermost square root first and then proceed outward.

   • Example: \(\sqrt{5 + \sqrt{20}}\)
   • Simplify: \(\sqrt{20} = 2\sqrt{5}\)
   • Result: \(\sqrt{5 + 2\sqrt{5}}\) (cannot be simplified further without additional techniques)

By understanding and addressing these special cases, you can accurately handle various scenarios in adding and subtracting square roots, ensuring your solutions are correct and simplified.

When adding or subtracting square roots, several common mistakes can lead to incorrect results. Here are some key points to keep in mind to avoid these errors:

• Not Simplifying Radicals First

  Always simplify the radicals before attempting to add or subtract them. For example, \(\sqrt{18}\) should be simplified to \(3\sqrt{2}\) before combining it with other square roots.

• Combining Unlike Terms

  Only combine like terms, which means the radicands (the numbers inside the square root) must be identical. For instance, you can combine \(2\sqrt{3}\) and \(5\sqrt{3}\) to get \(7\sqrt{3}\), but you cannot combine \(\sqrt{2}\) and \(\sqrt{3}\) directly.

• Incorrectly Adding or Subtracting Coefficients

  Ensure you only add or subtract the coefficients of like terms. For example, with \(2\sqrt{5} + 3\sqrt{5}\), you add the coefficients \(2 + 3\) to get \(5\sqrt{5}\).

• Failing to Recognize Simplifiable Radicals

  Sometimes, different radicands can be simplified to like terms. For instance, \(\sqrt{8}\) can be simplified to \(2\sqrt{2}\), which might then be combined with another term like \(\sqrt{2}\).

• Ignoring the Order of Operations

  Follow the order of operations (PEMDAS/BODMAS) carefully when dealing with expressions involving square roots and other operations. Simplify the radicals first before performing addition or subtraction.

• Misapplying the Distributive Property

  When multiplying square roots, remember to correctly apply the distributive property. For example, \(\sqrt{a} \cdot (\sqrt{b} + \sqrt{c}) = \sqrt{a} \cdot \sqrt{b} + \sqrt{a} \cdot \sqrt{c}\).

• Forgetting to Rationalize Denominators

  If a fraction has a square root in the denominator, you must rationalize it. For example, \(\frac{1}{\sqrt{2}}\) should be rewritten as \(\frac{\sqrt{2}}{2}\) by multiplying the numerator and denominator by \(\sqrt{2}\).

By keeping these points in mind, you can avoid common mistakes and correctly perform addition and subtraction of square roots.

Practice your skills in adding and subtracting square roots with these example problems. Make sure to simplify the square roots where necessary and combine like terms.

Problem 1

Simplify: \(3\sqrt{2} + 4\sqrt{2}\)

Solution:

• The radicands are the same, so you can add the coefficients.
• \(3\sqrt{2} + 4\sqrt{2} = (3 + 4)\sqrt{2} = 7\sqrt{2}\)

Problem 2

Simplify: \(5\sqrt{3} - 2\sqrt{3}\)

Solution:

• The radicands are the same, so you can subtract the coefficients.
• \(5\sqrt{3} - 2\sqrt{3} = (5 - 2)\sqrt{3} = 3\sqrt{3}\)

Problem 3

Simplify: \(2\sqrt{5} + \sqrt{20}\)

Solution:

• First, simplify \(\sqrt{20}\). \(\sqrt{20} = \sqrt{4 \cdot 5} = 2\sqrt{5}\).
• Now add the terms: \(2\sqrt{5} + 2\sqrt{5} = (2 + 2)\sqrt{5} = 4\sqrt{5}\).

Problem 4

Simplify: \(7\sqrt{7} - 3\sqrt{7}\)

Solution:

• The radicands are the same, so you can subtract the coefficients.
• \(7\sqrt{7} - 3\sqrt{7} = (7 - 3)\sqrt{7} = 4\sqrt{7}\)

Problem 5

Simplify: \(\sqrt{12} + 2\sqrt{3}\)

Solution:

• First, simplify \(\sqrt{12}\). \(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\).
• Now add the terms: \(2\sqrt{3} + 2\sqrt{3} = (2 + 2)\sqrt{3} = 4\sqrt{3}\).

Problem 6

Simplify: \(3\sqrt{8} - \sqrt{18}\)

Solution:

• First, simplify each term. \(\sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2}\) and \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\).
• Now subtract the terms: \(3(2\sqrt{2}) - 3\sqrt{2} = 6\sqrt{2} - 3\sqrt{2} = 3\sqrt{2}\).

Problem 7

Simplify: \(4\sqrt{27} + 2\sqrt{75}\)

Solution:

• First, simplify each term. \(\sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}\) and \(\sqrt{75} = \sqrt{25 \cdot 3} = 5\sqrt{3}\).
• Now add the terms: \(4(3\sqrt{3}) + 2(5\sqrt{3}) = 12\sqrt{3} + 10\sqrt{3} = 22\sqrt{3}\).

Understanding advanced techniques for working with square roots can enhance your ability to simplify, add, and subtract these expressions efficiently. Here are some key methods to consider:

1. Simplifying Complex Radicals

Start by simplifying each radical to its simplest form. This involves breaking down the radicand (the number inside the square root) into its prime factors and simplifying where possible.

For example:

1. \(\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\)
2. \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)

Once simplified, you can more easily identify like radicals.

2. Combining Like Radicals

Like radicals have the same radicand and can be combined by adding or subtracting their coefficients.

For example:

• \(3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2}\)
• \(7\sqrt{3} - 4\sqrt{3} = (7 - 4)\sqrt{3} = 3\sqrt{3}\)

3. Rationalizing the Denominator

Rationalizing the denominator involves removing the square root from the denominator of a fraction. This is done by multiplying both the numerator and the denominator by the same square root or its conjugate.

For example:

1. \(\frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5}\)
2. \(\frac{2}{3+\sqrt{2}} \times \frac{3-\sqrt{2}}{3-\sqrt{2}} = \frac{2(3-\sqrt{2})}{(3+\sqrt{2})(3-\sqrt{2})} = \frac{6-2\sqrt{2}}{9-2} = \frac{6-2\sqrt{2}}{7}\)

4. Utilizing the Distributive Property

When dealing with expressions that involve distributing a square root over a sum or difference, apply the distributive property effectively.

For example:

• \(\sqrt{2}(3 + \sqrt{3}) = 3\sqrt{2} + \sqrt{6}\)
• \(\sqrt{3}(2\sqrt{3} + \sqrt{5}) = 2(\sqrt{3} \cdot \sqrt{3}) + \sqrt{3 \cdot 5} = 2 \cdot 3 + \sqrt{15} = 6 + \sqrt{15}\)

5. Simplifying Expressions Involving Multiple Radicals

Combine and simplify expressions with different radicands by breaking them down to their simplest forms and then looking for common factors.

For example:

• \(3\sqrt{8} + 5\sqrt{2}\)

Simplify \(\sqrt{8} = 2\sqrt{2}\), then:

• \(3 \cdot 2\sqrt{2} + 5\sqrt{2} = 6\sqrt{2} + 5\sqrt{2} = 11\sqrt{2}\)

Mastering these advanced techniques can greatly enhance your proficiency in working with square roots, making complex problems more manageable and solvable.

Square roots play a crucial role in various real-life applications across different fields. Here are some notable examples:

• Finance:

  Square roots are used to calculate stock market volatility, which measures how much a stock's price varies over time. This involves taking the square root of the return variance, helping investors assess the risk of investments.

• Architecture and Engineering:

  In structural engineering, square roots help determine the natural frequency of structures such as bridges and buildings. This is essential for predicting how these structures will respond to different loads and environmental conditions.

• Science:

  Square roots are utilized in various scientific calculations, including determining the velocity of moving objects, the intensity of sound waves, and the amount of radiation absorbed by materials. These calculations are vital for scientific research and technological development.

• Statistics:

  In statistics, square roots are used to calculate standard deviation, which measures the amount of variation or dispersion in a set of data. Standard deviation is the square root of the variance, providing insights into data distribution.

• Geometry:

  Square roots are fundamental in geometry, especially when solving problems involving right triangles and other polygons. The Pythagorean theorem, for example, involves calculating the hypotenuse of a right triangle using square roots.

• Computer Science and Cryptography:

  Square roots are used in computer science for encryption algorithms, image processing, and game physics. Cryptography employs square roots in generating secure digital signatures and key exchange systems, ensuring data security.

• Navigation:

  Square roots help compute distances between points on a map or globe. For example, pilots use square roots to calculate the distance and direction between two points on a flight plan.

• Electrical Engineering:

  Square roots are used to calculate power, voltage, and current in electrical circuits. These calculations are crucial for designing and analyzing electrical systems like power grids and electronic devices.

• Photography:

  The aperture of a camera lens, which controls the amount of light entering the camera, is expressed as an f-number. The area of the aperture is proportional to the square of the f-number, affecting the exposure and depth of field in photography.

• Telecommunications:

  In wireless communication, signal strength decreases with distance, following the inverse square law. This principle is used to design and optimize telecommunication systems.

These examples illustrate the wide-ranging applications of square roots in various fields, highlighting their importance in both theoretical and practical contexts.

Understanding how to add and subtract square roots is essential for solving various mathematical problems. Throughout this guide, we have explored the fundamental concepts and steps necessary to handle square roots effectively. Here is a concise summary of the key points covered:

• Simplification: Always simplify the square roots to their simplest form before performing any operations. For example, \( \sqrt{18} \) can be simplified to \( 3\sqrt{2} \).
• Combining Like Terms: You can only add or subtract square roots if they have the same radicand. For instance, \( 2\sqrt{3} + 5\sqrt{3} = 7\sqrt{3} \), but \( 2\sqrt{3} + \sqrt{5} \) cannot be combined directly.
• Steps to Add/Subtract:
  1. Simplify each radical expression individually.
  2. Combine like terms by adding or subtracting the coefficients of square roots with the same radicand.
• Advanced Techniques: When dealing with more complex expressions, look for opportunities to factor and simplify further to ensure all square roots are in their simplest forms.
• Real-Life Applications: Square roots are used in various fields such as architecture, engineering, and physics to solve real-world problems involving areas, volumes, and distances.
• Common Mistakes: Avoid common errors such as adding square roots with different radicands or neglecting to simplify before combining terms.

By mastering these concepts and techniques, you can confidently tackle problems involving the addition and subtraction of square roots. Practice regularly to enhance your skills and apply these methods to more complex mathematical challenges.

Remember, the key to success is a solid understanding of the properties of square roots and consistent practice. Keep exploring and applying these principles, and you will find that working with square roots becomes second nature.