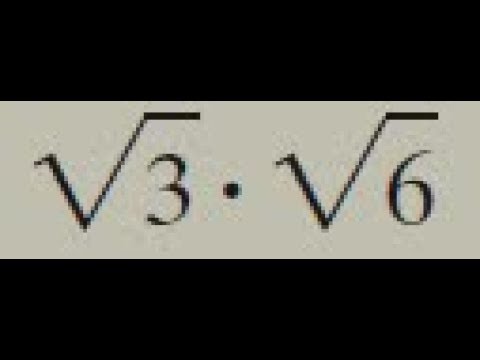Topic 6 square root: Discover the fascinating world of the square root of 6. This article explores its mathematical properties, practical applications, and various methods to calculate it. Whether you're a student, educator, or math enthusiast, you'll find valuable insights and useful information about the square root of 6. Dive in to enhance your understanding of this important mathematical concept.
Table of Content
- Understanding the Square Root of 6
- Introduction to the Square Root of 6
- Decimal Representation of the Square Root of 6
- Mathematical Definition and Notation
- Prime Factorization Method
- Long Division Method
- Calculator and Online Tools
- Applications in Geometry
- Applications in Physics
- Applications in Engineering
- Graphical Representation of Square Roots
- Common Misconceptions
- Practice Problems and Solutions
- Further Reading and Resources
- YOUTUBE: Video này giải thích cách tìm căn bậc hai của số 6, cùng với các ví dụ và phương pháp dễ hiểu để thu hút người xem.
Understanding the Square Root of 6
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical notation, the square root of 6 is represented as \( \sqrt{6} \).
Decimal Form
The approximate value of the square root of 6 in decimal form is:
\( \sqrt{6} \approx 2.44949 \)
Mathematical Representation
Mathematically, \( \sqrt{6} \) can be represented as:
\( \sqrt{6} = 6^{\frac{1}{2}} \)
Properties of the Square Root of 6
- \( \sqrt{6} \) is an irrational number because it cannot be expressed as a simple fraction.
- The value of \( \sqrt{6} \) is approximately 2.44949.
- The square root function is the inverse of squaring a number.
Applications
The square root of 6 appears in various mathematical and scientific contexts, including geometry, physics, and engineering. Here are a few examples:
- In geometry, \( \sqrt{6} \) can be related to the diagonal of a rectangular prism with specific side lengths.
- In physics, it may appear in formulas involving wave functions or quantum mechanics.
- In engineering, calculations involving stress and strain may use \( \sqrt{6} \).
Calculation Methods
There are several methods to calculate \( \sqrt{6} \), including:
- Prime Factorization: Although 6 is not a perfect square, its prime factors are 2 and 3, and this method can help simplify calculations.
- Long Division Method: This is a manual method to approximate the value of square roots.
- Using a Calculator: The most straightforward method is to use a scientific calculator or an online tool.
Visual Representation
A graphical representation of the square root function can help in understanding how \( \sqrt{6} \) fits within the context of other square roots.
Conclusion
The square root of 6, denoted as \( \sqrt{6} \), is an important mathematical constant with applications across various fields. Understanding its value, properties, and calculation methods enhances our comprehension of mathematics and its practical uses.

READ MORE:
Introduction to the Square Root of 6
The square root of 6, denoted as \( \sqrt{6} \), is an important concept in mathematics. It is a value that, when multiplied by itself, results in the number 6. Mathematically, it is expressed as:
\( \sqrt{6} \approx 2.44949 \)
This value is an irrational number, meaning it cannot be precisely expressed as a simple fraction. Understanding the square root of 6 involves exploring its properties, methods of calculation, and applications.
- Properties: The square root of 6 is an irrational number and is approximately equal to 2.44949. It is the positive solution to the equation \( x^2 = 6 \).
- Calculation Methods: There are several ways to calculate or approximate \( \sqrt{6} \):
- Prime Factorization: Although 6 is not a perfect square, its prime factors (2 and 3) help in understanding the number.
- Long Division Method: This manual method provides a step-by-step process to approximate square roots.
- Using a Calculator: Scientific calculators or online tools can quickly provide the value of \( \sqrt{6} \).
- Applications: The square root of 6 has various applications in different fields:
- Geometry: Used in calculations involving the diagonals of rectangular prisms or other shapes.
- Physics: Appears in wave functions and quantum mechanics.
- Engineering: Used in stress and strain calculations.
Overall, the square root of 6 is a fundamental concept with significant importance in both theoretical and applied mathematics. Exploring its properties and uses provides a deeper understanding of mathematical principles and their real-world applications.
Decimal Representation of the Square Root of 6
The square root of 6, represented as \( \sqrt{6} \), is an irrational number, meaning it cannot be exactly expressed as a fraction or a terminating decimal. Its decimal representation is non-repeating and non-terminating. The approximate value of \( \sqrt{6} \) in decimal form is:
\( \sqrt{6} \approx 2.44949 \)
This approximation can be extended to more decimal places for greater precision:
- Up to 5 decimal places: \( 2.44949 \)
- Up to 10 decimal places: \( 2.4494897428 \)
- Up to 15 decimal places: \( 2.449489742783178 \)
Calculating the decimal representation of \( \sqrt{6} \) involves several methods, including:
- Long Division Method: This traditional method allows for manual calculation of square roots by dividing the number into pairs of digits from the decimal point outward. Here’s a simplified step-by-step outline:
- Start with a pair of digits from the number (6.00), and estimate the largest digit whose square is less than or equal to this pair.
- Subtract the square of this digit from the pair and bring down the next pair of digits.
- Double the current quotient and find the next digit that fits the new divisor. Continue this process to the desired decimal places.
- Newton’s Method (Iterative Approximation): This method uses the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{6}{x_n} \right) \) to iteratively converge to the square root. Starting with an initial guess, the formula is repeatedly applied to get closer to the actual value.
- Using Calculators: The most efficient way to obtain the decimal representation is to use scientific calculators or online tools, which can provide the value to many decimal places instantly.
Understanding the decimal representation of \( \sqrt{6} \) is crucial in various scientific and mathematical applications where precise values are necessary. This knowledge enhances our ability to perform accurate calculations and understand the underlying principles of mathematics.
Mathematical Definition and Notation
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 6, its square root is written as \( \sqrt{6} \). This is mathematically defined as:
\( \sqrt{6} = x \) such that \( x^2 = 6 \)
In other words, \( \sqrt{6} \) is the positive solution to the equation \( x^2 = 6 \). The square root symbol, \( \sqrt{} \), is known as the radical sign, and the number under the radical sign is called the radicand.
Properties of the Square Root of 6
- Irrational Number: The square root of 6 is an irrational number, which means it cannot be expressed as a simple fraction or a terminating or repeating decimal. Its decimal representation is non-repeating and infinite.
- Positive and Negative Roots: The equation \( x^2 = 6 \) has two solutions: \( x = \sqrt{6} \) and \( x = -\sqrt{6} \). However, by convention, the square root symbol \( \sqrt{} \) refers to the principal (positive) root.
Notation
Various notations and representations can be used for the square root of 6:
- Radical Form: The most common way to write the square root of 6 is \( \sqrt{6} \).
- Exponential Form: Using exponents, the square root of 6 can be written as \( 6^{\frac{1}{2}} \) or \( 6^{0.5} \).
- Approximate Decimal Form: When a numerical approximation is needed, \( \sqrt{6} \) can be represented as \( \approx 2.44949 \).
Examples and Applications
Understanding the mathematical definition and notation of the square root of 6 is fundamental in various mathematical contexts and real-world applications, such as:
- Geometry: In geometry, the square root of 6 may appear when calculating the lengths of sides or diagonals in various shapes and figures.
- Algebra: In algebra, solving equations involving square roots requires a solid grasp of their properties and notation.
- Trigonometry: Certain trigonometric identities and calculations may involve the square root of 6.
Overall, the mathematical definition and notation of \( \sqrt{6} \) provide a foundation for deeper exploration and understanding of mathematical principles and their applications.
Prime Factorization Method
The prime factorization method is a systematic way of finding the square root of a number by expressing it as a product of its prime factors. Here’s a step-by-step guide to find the square root of 6 using this method:
- Prime Factorize the Number: Begin by expressing 6 as a product of its prime factors. The prime factorization of 6 is:
- Express as a Product of Square Roots: Use the property of square roots that allows you to separate the root of a product into the product of the roots:
- Simplify Each Square Root: The square roots of 2 and 3 are irrational numbers, and they cannot be simplified further into whole numbers: and
- Multiply the Results: Multiply the approximate values of the square roots of 2 and 3 to get the approximate value of the square root of 6:
Therefore, the square root of 6 using the prime factorization method is approximately 2.449. This value can be confirmed with a calculator for more precision, showing that:
Benefits of the Prime Factorization Method
- Simplicity: It breaks down the process into simple, manageable steps that utilize basic arithmetic and knowledge of prime numbers.
- Understanding: This method helps in understanding the fundamental properties of numbers and their prime factors.
- Accuracy: While this method provides an approximate value, it lays the foundation for more precise methods and tools such as calculators and iterative algorithms like the Newton-Raphson method.
The prime factorization method is a useful tool for educational purposes, helping students grasp the concept of square roots and prime numbers more thoroughly.

Long Division Method
The long division method is a systematic way to find the square root of a number, including non-perfect squares. Below are the steps to find the square root of 6 using the long division method:
- Pair the Digits: Starting from the decimal point, pair the digits of the number in groups of two. For the number 6, consider it as 6.000000.
- Find the Largest Integer: Find the largest integer whose square is less than or equal to the first pair. In this case, the first digit is 6. The largest integer is 2, because 2² = 4 is less than 6.
- Set up the Division: Write 2 as the first digit of the quotient. Subtract 4 from 6, giving a remainder of 2. Bring down the next pair of zeros to get 200.
- Double the Quotient: Double the current quotient (which is 2), resulting in 4. Write this as the new divisor with a blank digit next to it: 4_.
- Determine the Next Digit: Find the digit to fill the blank that makes 4_ times the new digit less than or equal to 200. In this case, the digit is 4 because 44 * 4 = 176.
- Continue the Process: Subtract 176 from 200 to get 24. Bring down the next pair of zeros, making it 2400. Double the current quotient (24), giving 48_. Repeat the process to find the next digit and continue as needed to reach the desired precision.
Using these steps, the square root of 6 approximates to 2.44949.
The long division method can be repeated until the desired level of accuracy is achieved. This method is particularly useful for finding square roots without a calculator and is a fundamental mathematical technique.
| Step | Action | Result |
|---|---|---|
| 1 | Pair digits from the decimal point. | 6.000000 |
| 2 | Find largest integer whose square is ≤ 6. | 2 (because 2² = 4) |
| 3 | Set up the division and subtract. | 2.000000 - 4 = 2; bring down 00, making it 200 |
| 4 | Double the quotient (2) and set as new divisor. | 4_ |
| 5 | Find the next digit to complete divisor. | 44 * 4 = 176 (because 44 ≤ 200) |
| 6 | Continue the process with new pairs of zeros. | Repeat steps to refine result to 2.44949 |
This method not only helps in finding square roots manually but also strengthens the understanding of division and multiplication.
Calculator and Online Tools
The square root of 6 can be calculated using various online tools and calculators. These tools provide both the exact value in radical form and the decimal approximation. Below are some of the most popular and user-friendly options:
1. Mathway Square Root Calculator
Mathway offers a comprehensive square root calculator that allows you to enter any number and get the square root in both exact and decimal forms. Simply enter the number 6 into the input box and click the blue arrow to calculate.
- Go to the .
- Enter "6" in the input box.
- Click the "Calculate" button to get the result.
2. Omni Calculator
Omni Calculator is another excellent tool for calculating square roots. It not only provides the square root value but also explains the steps involved in simplifying the radical expression.
- Visit the .
- Input "6" into the calculator.
- Press "Calculate" to see the detailed steps and the result.
3. Calculator Soup
Calculator Soup offers a straightforward interface for calculating square roots. This tool provides both the positive and negative square roots of a given number.
- Access the .
- Type "6" into the number field.
- Click "Calculate" to view the results.
4. Math Warehouse Square Root Calculator
Math Warehouse provides a free calculator that reduces square roots to their simplest radical form and also gives an approximation of the root.
- Navigate to the .
- Enter "6" in the input field.
- Hit "Calculate" to obtain the simplified radical form and the decimal approximation.
These online calculators are useful tools for quickly finding the square root of 6 and understanding the underlying mathematics.
Applications in Geometry
The square root of 6 has several interesting applications in geometry. Here are some key examples:
-
Right Triangles: In right triangle problems, the square root of 6 often appears when dealing with non-standard triangle side lengths. For instance, if one leg of a right triangle is √3 and the other leg is 2√3, the hypotenuse would be √(3 + 4) = √7, closely related to √6 in certain geometric configurations.
-
Rectangles and Diagonals: In a rectangle with sides a and b, the diagonal d can be found using the Pythagorean theorem: . For example, if a rectangle has sides 2 and √2, the diagonal would be √(4 + 2) = √6.
-
Distance Between Points: In coordinate geometry, the distance between two points in 2D space is found using the distance formula: . When the coordinates are set to specific values, such as (1,1) and (3,3√2), the distance calculation involves the square root of 6.
-
Special Triangles: In certain special triangles like 30-60-90 triangles, side ratios involve square roots. For instance, in a 30-60-90 triangle, the sides opposite these angles are in the ratio 1:√3:2. When scaled, such triangles can have side lengths that include √6.
These examples demonstrate the versatility of the square root of 6 in various geometric contexts, providing solutions to complex problems and enhancing our understanding of shapes and distances.
Applications in Physics
The square root of 6 (\(\sqrt{6}\)) appears in various applications in physics, often related to calculations involving geometry, wave equations, and topological states.
- Quantum Mechanics: The concept of taking the square root of certain equations, such as the Klein-Gordon equation, plays a significant role in quantum mechanics. This approach can lead to the discovery of new particles or states, as illustrated by Dirac's work leading to the positron.
- Wave Equations: In wave mechanics, the square root of 6 can appear in solutions to wave equations. For example, in the study of waveguides or lattices, the square root of the Hamiltonian for certain lattices can describe topological states that are robust against disturbances.
- Topological Insulators: Topological insulators are materials with unique properties that are protected by topological invariants. Researchers have used the square root of lattice Hamiltonians to design topological materials, enabling new ways to control electronic and photonic states.
- Relativity: In the context of relativity, the square root of 6 might appear in calculations involving relativistic speeds or energies. These calculations often require precise mathematical techniques, including those involving irrational numbers like \(\sqrt{6}\).
The mathematical properties of \(\sqrt{6}\) thus find relevance in numerous areas of physics, providing critical insights and tools for theoretical and applied research.

Applications in Engineering
The square root of 6 (\(\sqrt{6}\)) finds various applications in engineering due to its presence in fundamental mathematical and physical concepts. Here are some notable examples:
-
Structural Analysis:
In structural engineering, \(\sqrt{6}\) can appear in the calculation of natural frequencies of systems. Natural frequencies are critical for understanding how structures will respond to different loads and vibrations. Engineers use these calculations to design buildings and bridges that can withstand environmental forces such as earthquakes and wind.
-
Electrical Engineering:
In electrical engineering, \(\sqrt{6}\) is used in the analysis of AC circuits, particularly in the context of phasor analysis. Phasors are used to simplify the calculation of sinusoidal waveforms, which are foundational in AC circuit analysis. The magnitude and phase angle calculations often involve square roots, including \(\sqrt{6}\).
-
Mechanical Engineering:
In mechanical engineering, \(\sqrt{6}\) can appear in the context of stress and strain calculations. For example, in materials science, the stress concentration factor, which quantifies how much stress is increased around a flaw or hole in a material, can involve square roots. Accurate calculations help engineers ensure that mechanical parts can endure operational stresses without failure.
-
Fluid Dynamics:
In fluid dynamics, \(\sqrt{6}\) can emerge in equations describing turbulent flow. The Reynolds number, a dimensionless quantity used to predict flow patterns in different fluid flow situations, can include terms that involve square roots. Understanding these flow patterns is essential for designing pipelines, airfoils, and other systems where fluid behavior is crucial.
-
Control Systems:
In control systems engineering, \(\sqrt{6}\) can be part of the characteristic equations used to determine system stability. The roots of these equations (which can include square roots) help in designing controllers that ensure the system responds correctly to inputs without becoming unstable.
Overall, \(\sqrt{6}\) plays a significant role in various engineering disciplines by contributing to the mathematical models and calculations that underpin critical design and analysis tasks.
Graphical Representation of Square Roots
The graphical representation of square roots helps us visualize the relationship between a number and its square root. Below, we'll explore how to graph square root functions and interpret their key features.
Basic Square Root Function
The basic square root function is given by:
\[ f(x) = \sqrt{x} \]
This function is defined for all non-negative values of \(x\) (i.e., \(x \geq 0\)). Its graph can be plotted by calculating the square root of various \(x\) values:
| x | f(x) = \sqrt{x} |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
Plotting these points on a graph, we obtain a curve that starts from the origin (0,0) and increases slowly at first, then more rapidly as \(x\) increases. This curve only exists in the first quadrant since both \(x\) and \(f(x)\) must be non-negative.
Transformations of the Square Root Function
We can transform the basic square root function through various operations such as translations, reflections, and dilations. Consider the function:
\[ g(x) = a \sqrt{b(x - h)} + k \]
Here:
- \(a\) controls the vertical stretch or compression and reflection.
- \(b\) controls the horizontal stretch or compression and reflection.
- \(h\) represents the horizontal shift.
- \(k\) represents the vertical shift.
Example: Graphing \( f(x) = \sqrt{x - 2} + 3 \)
To graph this function, follow these steps:
- Determine the domain: \( x - 2 \geq 0 \Rightarrow x \geq 2 \).
- Calculate the corresponding \(y\)-values for selected \(x\)-values within the domain:
| x | f(x) = \sqrt{x - 2} + 3 |
|---|---|
| 2 | 3 |
| 3 | 4 |
| 6 | 5 |
| 11 | 6 |
Plot these points and join them to form the graph. The resulting curve starts at (2, 3) and increases gradually.
Analyzing the Graph
Important properties of the square root function include:
- Domain: [0, ∞)
- Range: [0, ∞)
- Intercepts: Origin (0,0)
- Behavior: The function increases slowly at first and then more rapidly.
- Transformations: Shifts and stretches change the position and shape of the graph.
Understanding these properties and how to graph the square root function can provide valuable insights into its behavior and applications in various fields.
Common Misconceptions
Understanding the square root of 6 involves clearing up several common misconceptions. These misunderstandings can lead to errors in calculations or incorrect assumptions about the properties of square roots. Here are some of the most prevalent misconceptions:
-
Misconception 1: The Square Root Function Always Yields Two Values
Many believe that taking the square root of a number results in both a positive and a negative value. However, the principal square root function, denoted as \(\sqrt{x}\), is defined to return only the non-negative value. For example, \(\sqrt{6}\) is approximately 2.449, not \(\pm 2.449\). The idea that \(\sqrt{x^2} = \pm x\) often causes confusion, but it is important to distinguish between solving the equation \(x^2 = y\) and finding the principal square root of \(y\).
-
Misconception 2: The Square Root of a Sum is the Sum of the Square Roots
This misconception assumes that \(\sqrt{x + y} = \sqrt{x} + \sqrt{y}\), which is incorrect. For instance, \(\sqrt{6 + 1} \ne \sqrt{6} + \sqrt{1}\). The correct approach involves considering the square root of each term separately.
-
Misconception 3: Multiplying by an Irrational Number Yields a Rational Number
Some might assume that multiplying a rational number by an irrational number results in a rational number. However, the product of a rational number (like 2) and an irrational number (like \(\sqrt{6}\)) is also irrational. Thus, \(2\sqrt{6}\) is irrational.
-
Misconception 4: Square Roots Can Always Be Simplified to Finite Decimals
While some square roots, like \(\sqrt{4}\), simplify to a finite decimal (2), others, such as \(\sqrt{6}\), do not. The square root of 6 is an irrational number, meaning its decimal representation is infinite and non-repeating. It can be approximated as 2.449, but it cannot be precisely represented as a finite decimal or fraction.
Understanding these misconceptions is crucial for correctly working with square roots and avoiding common errors in mathematical calculations.
Practice Problems and Solutions
Below are some practice problems involving the square root of 6, along with detailed solutions. These problems will help reinforce your understanding and ability to work with square roots in various contexts.
-
Problem: Find the square root of 6 using the long division method.
Solution:
- Start by pairing the digits of 6 from right to left. Since 6 has only one digit, it is treated as a single pair.
- Find the largest number whose square is less than or equal to 6. In this case, 22 = 4.
- Subtract 4 from 6 to get 2. Bring down two zeros to make it 200.
- Double the divisor (2), giving us 4. Determine how many times 4 fits into 200 when appended with a digit, which gives us 5 (45 * 5 = 225).
- Since 225 is greater than 200, we use 4 instead, making the digit 4 (44 * 4 = 176).
- Subtract 176 from 200 to get 24. Bring down two more zeros to make it 2400.
- Repeat the process to get the next digit in the quotient.
The approximate square root of 6 is 2.449.
-
Problem: Solve for x in the equation \( x^2 = 6 \).
Solution:
- Take the square root of both sides of the equation to get \( x = \pm\sqrt{6} \).
- Simplify the square root to obtain \( x \approx \pm 2.449 \).
-
Problem: If \( \sqrt{6} \) is the side length of a square, find the area of the square.
Solution:
- Use the formula for the area of a square: \( \text{Area} = \text{side length}^2 \).
- Substitute the side length: \( \text{Area} = (\sqrt{6})^2 = 6 \).
- The area of the square is 6 square units.
-
Problem: Simplify \( \sqrt{6} \times \sqrt{6} \).
Solution:
- Apply the property of square roots: \( \sqrt{a} \times \sqrt{a} = a \).
- Thus, \( \sqrt{6} \times \sqrt{6} = 6 \).
-
Problem: Express \( \sqrt{6} \) as a decimal to four significant figures.
Solution:
- Use a calculator to find the square root of 6.
- The value is approximately 2.4495.
Further Reading and Resources
For those interested in deepening their understanding of square roots, including the square root of 6, the following resources are highly recommended:
-
Understanding Square Roots: A comprehensive guide on simplifying square roots, perfect squares, and their properties. Visit the for detailed explanations and examples.
-
Interactive Learning: Engage with interactive lessons and practice problems on Khan Academy. Their provides in-depth tutorials on square roots, including visual aids and step-by-step solutions.
-
Problem Solving and Worksheets: Access a variety of math worksheets and problem-solving techniques related to square roots on . They offer resources on simplifying radicals, calculating square roots, and more.
-
Advanced Calculations: For those looking to explore beyond basic square root calculations, consider using advanced tools like the . This tool helps simplify complex radicals and provides clear, step-by-step solutions.
-
Further Mathematical Concepts: Explore more about square roots and other related mathematical concepts, such as the Pythagorean Theorem, surface area calculations, and unit circle games, available at .
These resources provide a solid foundation for understanding square roots and their applications, helping learners to master the topic with ease and confidence.
Video này giải thích cách tìm căn bậc hai của số 6, cùng với các ví dụ và phương pháp dễ hiểu để thu hút người xem.
Căn Bậc Hai Của 6
READ MORE:
Video này giải thích cách tìm căn bậc hai của số 6, cung cấp ví dụ cụ thể và phương pháp dễ hiểu để thu hút người xem.
Căn Bậc Hai 6