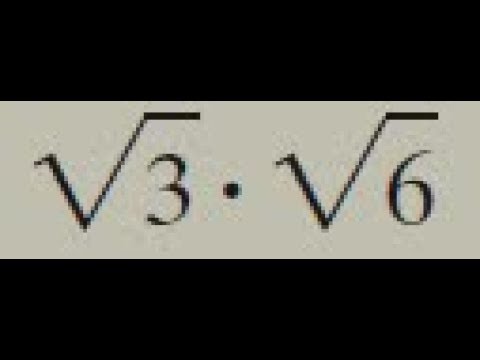Topic how to add square root and whole number: Learning how to add a square root and a whole number is simpler than you might think. This guide will walk you through the process step-by-step, making it easy to understand and apply. Whether you're a student or just curious, you'll find everything you need to master this fundamental math concept.
Table of Content
- How to Add a Square Root and a Whole Number
- Introduction to Adding Square Roots and Whole Numbers
- Understanding Square Roots
- Understanding Whole Numbers
- Basic Principles of Addition
- Simplifying Square Root Expressions
- Examples of Adding Square Roots and Whole Numbers
- Common Mistakes to Avoid
- Practical Applications
- FAQs About Square Roots and Whole Numbers
- Advanced Concepts and Techniques
- Conclusion and Key Takeaways
- YOUTUBE: Hướng dẫn chi tiết về cách cộng và trừ số học và số nguyên với ký hiệu radicals, giúp bạn nắm vững các khái niệm toán học cơ bản và nâng cao.
How to Add a Square Root and a Whole Number
Adding a square root and a whole number is a straightforward process in mathematics. Here, we will break down the steps and provide examples to illustrate the concept clearly.
Steps to Add a Square Root and a Whole Number
- Identify the terms: Determine the square root term and the whole number. For example, if you need to add √3 and 5, √3 is the square root term and 5 is the whole number.
- Combine the terms: Simply write the square root term and the whole number together with a plus sign between them. Using our example, this results in the expression: √3 + 5.
- Simplify if possible: In many cases, the expression will remain in its combined form since a square root is an irrational number and cannot be simplified further with a whole number. Therefore, √3 + 5 is the final answer.
Examples
\(\sqrt{2} + 4\) \(\sqrt{5} + 3\) \(\sqrt{10} + 7\)
Additional Notes
When adding a square root and a whole number, the result is typically left in its combined form because they represent different types of numbers (irrational and rational, respectively). This combined expression is generally considered the simplest form unless further context or operations are applied.
For educational purposes, here are a few more examples with detailed steps:
| Expression | Result |
|---|---|
As shown in the table, the expressions remain in their combined form since the square roots cannot be simplified to mix with whole numbers.
READ MORE:
Introduction to Adding Square Roots and Whole Numbers
Adding square roots and whole numbers might seem challenging at first, but it is a fundamental mathematical concept that can be easily understood with practice. This section will introduce you to the basic principles and provide a step-by-step approach to mastering this skill.
When adding a square root and a whole number, you are essentially combining two different types of numbers: rational (whole numbers) and irrational (square roots that cannot be simplified to a whole number).
Here are the steps to follow:
- Identify the terms: Determine the square root term and the whole number. For example, in the expression \(\sqrt{3} + 5\), \(\sqrt{3}\) is the square root term and 5 is the whole number.
- Write the expression: Combine the square root and the whole number into a single expression, such as \(\sqrt{3} + 5\).
- Simplify if possible: While the expression often remains in its combined form, always check if the square root can be simplified. For instance, \(\sqrt{4}\) can be simplified to 2, making \(\sqrt{4} + 3\) equivalent to \(2 + 3 = 5\).
In most cases, the result will remain a combined expression, as square roots typically do not simplify to integers. Here are some examples to illustrate this:
\(\sqrt{2} + 4\) \(\sqrt{5} + 3\) \(\sqrt{7} + 2\)
Understanding how to add square roots and whole numbers is crucial for solving various mathematical problems. With this foundational knowledge, you will be well-equipped to tackle more complex mathematical concepts in the future.
Understanding Square Roots
A square root is a number that, when multiplied by itself, gives the original number. It is an essential concept in mathematics, often represented by the radical symbol \(\sqrt{}\). For example, the square root of 9 is 3, because \(3 \times 3 = 9\).
Here are the key points to understand about square roots:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are called perfect squares because their square roots are whole numbers (e.g., \(\sqrt{16} = 4\)).
- Non-Perfect Squares: Numbers that are not perfect squares have square roots that are irrational numbers, which cannot be expressed as a simple fraction. For example, \(\sqrt{2}\) is approximately 1.414 and cannot be precisely written as a fraction.
- Properties of Square Roots:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
Let's look at some examples to clarify:
| Number | Square Root |
|---|---|
| 4 | \(\sqrt{4} = 2\) |
| 9 | \(\sqrt{9} = 3\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
Understanding square roots is fundamental for various mathematical operations, including solving quadratic equations, working with exponents, and simplifying expressions. With practice, you will become more comfortable working with both perfect and non-perfect square roots.
Understanding Whole Numbers
Whole numbers are a fundamental part of mathematics and include all the non-negative integers, starting from zero and going upwards: 0, 1, 2, 3, 4, and so on. Whole numbers do not include fractions, decimals, or negative numbers.
Here are the key properties of whole numbers:
- Non-Negative: Whole numbers are always greater than or equal to zero.
- Closed Under Addition and Multiplication: Adding or multiplying two whole numbers always results in another whole number. For example, \(3 + 4 = 7\) and \(3 \times 4 = 12\).
- Identity Elements: The identity element for addition is 0, as adding 0 to any whole number does not change its value: \(n + 0 = n\). The identity element for multiplication is 1, as multiplying any whole number by 1 does not change its value: \(n \times 1 = n\).
- Order and Comparison: Whole numbers can be compared and ordered. For example, 5 is greater than 3, and 2 is less than 4.
Let's look at some examples to clarify:
| Operation | Example | Result |
|---|---|---|
| Addition | \(7 + 5\) | 12 |
| Multiplication | \(6 \times 4\) | 24 |
| Identity (Addition) | \(9 + 0\) | 9 |
| Identity (Multiplication) | \(8 \times 1\) | 8 |
Understanding whole numbers is crucial as they form the basis for more complex mathematical concepts and operations. Mastery of whole numbers enables you to perform arithmetic operations confidently and serves as a stepping stone to learning about integers, fractions, and decimals.
Basic Principles of Addition
Addition is one of the fundamental operations in mathematics, used to calculate the total or sum of two or more numbers. Understanding the basic principles of addition is essential for performing more complex mathematical operations, including adding square roots and whole numbers.
Here are the key principles of addition:
- Commutative Property: The order of the numbers being added does not affect the sum. For example, \(a + b = b + a\). This means \(2 + 3 = 3 + 2 = 5\).
- Associative Property: The way numbers are grouped when adding does not affect the sum. For example, \((a + b) + c = a + (b + c)\). This means \((2 + 3) + 4 = 2 + (3 + 4) = 9\).
- Identity Property: Adding zero to any number does not change the value of that number. For example, \(a + 0 = a\). This means \(5 + 0 = 5\).
Let's explore these principles with some examples:
| Principle | Example | Explanation |
|---|---|---|
| Commutative Property | \(4 + 5 = 5 + 4\) | Both expressions equal 9, demonstrating that order does not matter. |
| Associative Property | \((1 + 2) + 3 = 1 + (2 + 3)\) | Both expressions equal 6, showing that grouping does not matter. |
| Identity Property | \(7 + 0 = 7\) | Adding zero to any number leaves it unchanged. |
When adding square roots and whole numbers, these basic principles still apply. For instance, even though square roots are often irrational numbers, the commutative and associative properties help simplify the addition process.
Here is a step-by-step approach to adding square roots and whole numbers:
- Identify the terms: Determine the square root and whole number in the expression. For example, in \(\sqrt{3} + 4\), \(\sqrt{3}\) is the square root and 4 is the whole number.
- Combine the terms: Write the square root term and the whole number together with a plus sign between them. This results in the expression: \(\sqrt{3} + 4\).
- Simplify if possible: Check if the square root can be simplified or if it can be combined with the whole number. Typically, the expression remains in its combined form, such as \(\sqrt{3} + 4\).
By mastering these basic principles of addition, you will be well-equipped to handle more advanced mathematical problems, including those involving square roots and whole numbers.

Simplifying Square Root Expressions
Simplifying square root expressions is an important skill in mathematics, helping to make calculations easier and results clearer. Here are the steps to simplify square root expressions:
- Identify Perfect Squares:
Look for factors of the number under the square root that are perfect squares. Perfect squares include numbers like 1, 4, 9, 16, 25, etc. For example, in \(\sqrt{18}\), 9 is a perfect square factor because \(9 \times 2 = 18\).
- Rewrite the Square Root:
Express the square root as the product of the square root of the perfect square and the square root of the remaining factor. For example, \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2}\).
- Simplify the Square Root of the Perfect Square:
Calculate the square root of the perfect square. For example, \(\sqrt{9} = 3\), so \(\sqrt{18} = 3 \times \sqrt{2} = 3\sqrt{2}\).
- Combine Like Terms (if any):
If there are like terms in an expression, combine them. For example, in the expression \(2\sqrt{2} + 3\sqrt{2}\), the like terms can be combined to give \(5\sqrt{2}\).
Let's look at a few more examples to clarify:
| Expression | Steps | Simplified Form |
|---|---|---|
| \(\sqrt{50}\) | \(\sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\) | 5\(\sqrt{2}\) |
| \(\sqrt{32}\) | \(\sqrt{16 \times 2} = \sqrt{16} \times \sqrt{2} = 4\sqrt{2}\) | 4\(\sqrt{2}\) |
| \(\sqrt{72}\) | \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\) | 6\(\sqrt{2}\) |
Simplifying square root expressions makes it easier to work with them in further calculations and helps in recognizing patterns in problems. Practicing these steps will enhance your ability to handle square roots efficiently.
Examples of Adding Square Roots and Whole Numbers
Adding square roots and whole numbers may initially seem complex, but with practice, it becomes straightforward. Here are several examples to illustrate the process step by step:
Example 1: Adding \(\sqrt{3}\) and 5
- Identify the Terms:
The terms are \(\sqrt{3}\) and 5.
- Combine the Terms:
Write the expression as \(\sqrt{3} + 5\).
- Simplify:
The expression \(\sqrt{3}\) cannot be simplified further, so the final result is \(\sqrt{3} + 5\).
Example 2: Adding \(\sqrt{16}\) and 4
- Identify the Terms:
The terms are \(\sqrt{16}\) and 4.
- Simplify the Square Root:
\(\sqrt{16} = 4\).
- Combine the Terms:
The expression becomes \(4 + 4 = 8\).
- Final Result:
The final result is 8.
Example 3: Adding \(\sqrt{2}\) and 7
- Identify the Terms:
The terms are \(\sqrt{2}\) and 7.
- Combine the Terms:
Write the expression as \(\sqrt{2} + 7\).
- Simplify:
The expression \(\sqrt{2}\) cannot be simplified further, so the final result is \(\sqrt{2} + 7\).
Example 4: Adding \(\sqrt{9}\) and 3
- Identify the Terms:
The terms are \(\sqrt{9}\) and 3.
- Simplify the Square Root:
\(\sqrt{9} = 3\).
- Combine the Terms:
The expression becomes \(3 + 3 = 6\).
- Final Result:
The final result is 6.
Example 5: Adding \(\sqrt{5}\) and 2
- Identify the Terms:
The terms are \(\sqrt{5}\) and 2.
- Combine the Terms:
Write the expression as \(\sqrt{5} + 2\).
- Simplify:
The expression \(\sqrt{5}\) cannot be simplified further, so the final result is \(\sqrt{5} + 2\).
These examples illustrate that when the square root is a perfect square, it can be simplified to a whole number and combined directly with the other whole number. Otherwise, the expression remains in its combined form. With these steps, you can confidently add square roots and whole numbers in various mathematical problems.
Common Mistakes to Avoid
When adding square roots and whole numbers, there are several common mistakes that can lead to incorrect results. Here are some key points to keep in mind to avoid these errors:
- Assuming Square Roots Can Be Directly Added to Whole Numbers:
A common misconception is to treat square roots like regular numbers. For example, assuming that \( \sqrt{4} + 3 = 2 + 3 = 5 \) is correct. Instead, remember that \( \sqrt{4} = 2 \), so the expression simplifies correctly to 5, but the process should acknowledge the root first.
- Not Simplifying the Square Root First:
Always simplify the square root before adding it to the whole number. For example, instead of trying to add \( \sqrt{18} \) directly to a whole number, simplify \( \sqrt{18} \) to \( 3\sqrt{2} \) first.
- Ignoring the Properties of Square Roots:
Square roots have unique properties that must be considered. For instance, \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \), but this does not apply to addition. For addition, you cannot combine square roots unless they are like terms (i.e., \( \sqrt{a} + \sqrt{a} = 2\sqrt{a} \)).
- Combining Unlike Terms:
Ensure you are not combining unlike terms. For instance, \( \sqrt{2} + 3 \) cannot be simplified to a single term. The correct expression is simply \( \sqrt{2} + 3 \).
- Forgetting to Rationalize the Denominator:
If your addition results in a fraction with a square root in the denominator, you must rationalize it. For example, \( \frac{3}{\sqrt{2}} + 2 \) should be rationalized to \( \frac{3\sqrt{2}}{2} + 2 \).
By being aware of these common mistakes, you can ensure that your calculations involving the addition of square roots and whole numbers are accurate and correct.
Practical Applications
Understanding how to add square roots and whole numbers can be applied in various real-world scenarios. Here are some practical applications:
- Architecture and Construction: Square roots often appear in architectural designs and construction projects when dealing with areas and diagonals. For example, if the length of a side of a square is known, the diagonal can be calculated using the square root function, and adding whole numbers may be necessary to determine total measurements.
- Engineering: Engineers frequently use square roots in their calculations for designing mechanical parts, electrical circuits, and structures. Adding whole numbers to these square root values can help in computing total lengths, areas, or other measurements.
- Finance: In financial calculations, square roots can be used to determine volatility or standard deviation in investments. Adding whole numbers can be important when adjusting these values for practical financial analysis.
- Physics: Many physical formulas involve square roots, such as those calculating kinetic energy or wave speeds. Adding whole numbers can help in interpreting these results within a broader context or when combining multiple measurements.
Here are a few specific examples:
- Calculating the Diagonal of a Square Room:
- Suppose a room has a side length of 5 meters. The diagonal \(d\) can be calculated as:
\[ d = \sqrt{5^2 + 5^2} = \sqrt{50} \approx 7.07 \text{ meters} \]
- If you need to add 3 meters to account for additional space, the total measurement would be:
\[ 7.07 + 3 = 10.07 \text{ meters} \]
- Suppose a room has a side length of 5 meters. The diagonal \(d\) can be calculated as:
- Adjusting Measurements in Engineering:
- Consider a metal rod with a length that needs to be cut to fit a diagonal space in a frame where the sides are 4 meters each:
\[ \text{Diagonal} = \sqrt{4^2 + 4^2} = \sqrt{32} \approx 5.66 \text{ meters} \]
- If the design requires an additional 2 meters for fitting adjustments, the final length will be:
\[ 5.66 + 2 = 7.66 \text{ meters} \]
- Consider a metal rod with a length that needs to be cut to fit a diagonal space in a frame where the sides are 4 meters each:
- Combining Financial Metrics:
- Suppose an investment's standard deviation (a square root measure) is 1.5, and you need to add a risk-free rate of 2% for analysis:
\[ 1.5 + 2 = 3.5 \text{ (combined metric)} \]
- Suppose an investment's standard deviation (a square root measure) is 1.5, and you need to add a risk-free rate of 2% for analysis:
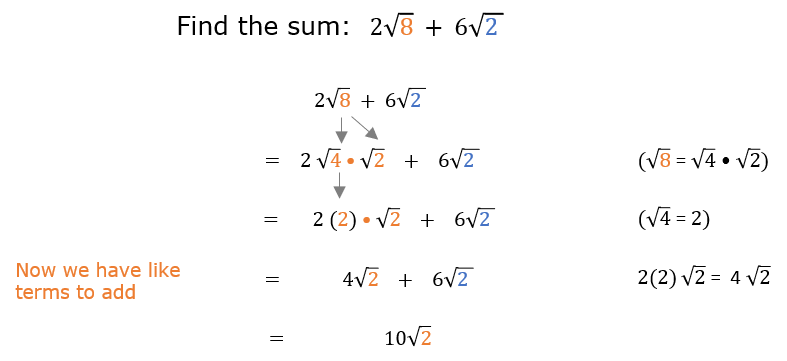
FAQs About Square Roots and Whole Numbers
Here are some frequently asked questions about adding square roots and whole numbers, along with detailed answers to help you understand the concepts better.
-
Q: Can you add a square root and a whole number?
A: Yes, you can add a square root and a whole number, but they are not like terms. For example, cannot be simplified further and remains as .
-
Q: How do you simplify a square root before adding it to a whole number?
A: To simplify a square root, look for perfect square factors. For instance, can be simplified to because and is .
-
Q: What are "like terms" when adding square roots?
A: "Like terms" in the context of square roots are terms that have the same radicand. For example, are like terms and can be added to get .
-
Q: Can all square roots be simplified?
A: No, not all square roots can be simplified to whole numbers or simpler square roots. For instance, and are already in their simplest form.
-
Q: What happens if the radicands are not the same when adding square roots?
A: If the radicands are not the same, you cannot directly add the square roots. For example, cannot be combined into a single term.
-
Q: Can square roots be added to each other if they have coefficients?
A: Yes, but you need to simplify the square roots first and then combine like terms. For example, simplifies to .
Advanced Concepts and Techniques
Adding square roots and whole numbers involves a few advanced concepts and techniques that can simplify the process and provide a deeper understanding of the mathematical principles involved. Here, we explore these advanced methods step-by-step.
1. Simplifying Radicals
Before adding square roots to whole numbers, it's essential to simplify the radicals wherever possible. Simplifying involves breaking down the radicand (the number inside the square root) into its prime factors and extracting any perfect squares.
For example:
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
2. Combining Like Radicals
Once simplified, only like radicals (those with the same radicand) can be combined by adding their coefficients, similar to combining like terms in algebra.
For example:
- \(3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}\)
- \(2\sqrt{3} + \sqrt{3} = 3\sqrt{3}\)
3. Rationalizing the Denominator
In some cases, square roots appear in the denominator of a fraction. Rationalizing the denominator involves eliminating the square root by multiplying the numerator and the denominator by a suitable radical.
For example:
- \(\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
- \(\frac{3}{\sqrt{5}} = \frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}\)
4. Using Decimal Approximations
For non-perfect square roots that cannot be simplified easily, converting the square root to a decimal approximation can help in practical calculations. This method is particularly useful in real-world applications where exact values are not necessary.
For example:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
Adding these to whole numbers then becomes straightforward:
- \(\sqrt{2} + 3 \approx 1.414 + 3 = 4.414\)
- \(\sqrt{3} + 5 \approx 1.732 + 5 = 6.732\)
5. Advanced Problem Solving
Let's explore some complex examples that illustrate these techniques:
- Example 1: Simplifying Before Adding
Add \(\sqrt{32}\) to 4.
Solution: \(\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}\). Therefore, the addition is \(4\sqrt{2} + 4\), which remains as it is because the terms are not like terms. - Example 2: Combining Like Radicals
Add \(\sqrt{50}\) to \(\sqrt{18}\).
Solution: \(\sqrt{50} = 5\sqrt{2}\) and \(\sqrt{18} = 3\sqrt{2}\). Thus, the addition is \(5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}\). - Example 3: Rationalizing the Denominator
Add \(\frac{1}{\sqrt{3}}\) to 2.
Solution: \(\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}\). Therefore, the addition is \(2 + \frac{\sqrt{3}}{3}\), which is \(\frac{6 + \sqrt{3}}{3}\).
By mastering these advanced techniques, you can handle more complex mathematical problems involving square roots and whole numbers with greater ease and accuracy.
Conclusion and Key Takeaways
Adding square roots and whole numbers may initially seem complex, but with an understanding of key principles and techniques, it becomes straightforward. Here are the essential points to remember:
- Simplification First: Always simplify the square root expressions as much as possible before attempting to add them. This can sometimes turn a radical into a whole number, making the addition easier.
- Like Terms: Only square roots with the same radicand (the number under the root) can be directly added. For example, \( \sqrt{2} + \sqrt{2} = 2\sqrt{2} \).
- Combining Whole Numbers: If a square root simplifies to a whole number, combine it with other whole numbers in the equation. For example, \( \sqrt{16} + 5 = 4 + 5 = 9 \).
- Approximation: For practical purposes, especially in non-exact scenarios, consider converting non-perfect square roots to their decimal form for easier addition with whole numbers. For example, \( \sqrt{2} \approx 1.414 \), so \( 1.414 + 3 \approx 4.414 \).
In summary, the key steps to successfully adding square roots and whole numbers involve simplification, recognizing and combining like terms, and knowing when to use decimal approximations. Mastery of these techniques will enhance your mathematical precision and problem-solving abilities.
Hướng dẫn chi tiết về cách cộng và trừ số học và số nguyên với ký hiệu radicals, giúp bạn nắm vững các khái niệm toán học cơ bản và nâng cao.
Cách Cộng & Trừ Số Học và Số Nguyên: Các Số Sử Dụng Ký Hiệu Radicals
READ MORE:
Video hướng dẫn cách cộng và trừ căn bậc hai, giúp bạn nắm vững các kỹ thuật toán học quan trọng.
Cách Cộng và Trừ Căn Bậc Hai