Topic square root of 6 rational or irrational: Is the square root of 6 rational or irrational? Uncover the mathematical proof and explore the fascinating properties of this number. Learn why it holds a unique place in mathematics, its significance, and how it fits into the broader context of rational and irrational numbers.
Table of Content
- Is the Square Root of 6 Rational or Irrational?
- Introduction
- Definition of Rational and Irrational Numbers
- Understanding the Square Root
- Mathematical Proof of Irrationality
- Historical Context and Significance
- Decimal Expansion of Square Root of 6
- Visual Representation
- Applications in Mathematics and Science
- Common Misconceptions
- YOUTUBE: Video cung cấp bằng chứng rằng căn bậc hai của bất kỳ số nguyên nào là vô tỷ, ngoại trừ các số chính phương.
Is the Square Root of 6 Rational or Irrational?
The square root of 6 is an interesting number that can be analyzed to determine whether it is rational or irrational. A rational number is one that can be expressed as the quotient of two integers, where the denominator is not zero. An irrational number, on the other hand, cannot be expressed in this way and has a non-repeating, non-terminating decimal expansion.
Analysis of the Square Root of 6
To determine if
- Assume that
\(\sqrt{6}\) is a rational number. This means it can be expressed as\(\frac{a}{b}\) , where\(a\) and\(b\) are integers with no common factors other than 1, and\(b \neq 0\) . - If
\(\sqrt{6} = \frac{a}{b}\) , then by squaring both sides, we get\(6 = \frac{a^2}{b^2}\) , which implies\(a^2 = 6b^2\) . - For
\(a^2\) to be divisible by 6, \(a\) must also be divisible by 6. Let \(a = 6k\) for some integer \(k\). - Substituting \(a = 6k\) into the equation \(a^2 = 6b^2\), we get \(36k^2 = 6b^2\), which simplifies to \(6k^2 = b^2\).
- Similarly, \(b^2\) must be divisible by 6, implying that \(b\) must also be divisible by 6.
- This means that both \(a\) and \(b\) share a common factor of 6, which contradicts our initial assumption that \(a\) and \(b\) have no common factors other than 1.
Therefore, our assumption that
Conclusion
The square root of 6 is an irrational number. This conclusion is based on the fact that assuming it is rational leads to a logical contradiction. As an irrational number,

READ MORE:
Introduction
The concept of rational and irrational numbers is fundamental in mathematics. A rational number can be expressed as a fraction
The square root of 6, denoted as
- Assume that
\(\sqrt{6}\) is a rational number, meaning it can be written as\(\frac{a}{b}\) , where\(a\) and\(b\) are integers with no common factors other than 1. - Square both sides:
\(\sqrt{6} = \frac{a}{b} \implies 6 = \frac{a^2}{b^2} \implies a^2 = 6b^2\) . - For
\(a^2\) to be divisible by 6,\(a\) must be divisible by 6. Let\(a = 6k\) for some integer\(k\) . - Substitute into the equation:
\(36k^2 = 6b^2 \implies b^2 = 6k^2\) . - This implies that
\(b\) is also divisible by 6, contradicting the assumption that\(a\) and\(b\) have no common factors.
This contradiction shows that our initial assumption was incorrect. Therefore, the square root of 6 is an irrational number. It cannot be expressed as a simple fraction and its decimal expansion goes on forever without repeating.
Definition of Rational and Irrational Numbers
To understand the nature of the square root of 6, it's essential to differentiate between rational and irrational numbers.
Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer. Mathematically, a number \( \frac{p}{q} \) is rational if:
- \( p \) and \( q \) are integers
- \( q \neq 0 \)
Examples of rational numbers include:
- \( \frac{1}{2} \) (which equals 0.5)
- \( -\frac{3}{4} \) (which equals -0.75)
- \( 5 \) (which can be written as \( \frac{5}{1} \))
Irrational Numbers
An irrational number, on the other hand, cannot be expressed as a simple fraction. Irrational numbers cannot be written as the quotient of two integers. Instead, their decimal expansions are non-repeating and non-terminating. Mathematically, a number is irrational if it cannot be written in the form \( \frac{p}{q} \) where \( p \) and \( q \) are integers with \( q \neq 0 \).
Examples of irrational numbers include:
- \( \sqrt{2} \)
- \( \pi \) (approximately 3.14159...)
- \( e \) (approximately 2.71828...)
Distinguishing Characteristics
The key differences between rational and irrational numbers can be summarized in the following table:
| Characteristic | Rational Numbers | Irrational Numbers |
|---|---|---|
| Definition | Can be expressed as \( \frac{p}{q} \) | Cannot be expressed as \( \frac{p}{q} \) |
| Decimal Expansion | Repeating or terminating | Non-repeating and non-terminating |
| Examples | \( \frac{1}{2}, \frac{3}{4}, 5 \) | \( \sqrt{2}, \pi, e \) |
By understanding these definitions, we can further explore whether the square root of 6 is rational or irrational in subsequent sections.
Understanding the Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, the square root of \( x \) is denoted as \( \sqrt{x} \). For instance, the square root of 6, represented as \( \sqrt{6} \), is the number that satisfies the equation:
\[ \sqrt{6} \times \sqrt{6} = 6 \]
To understand the concept of the square root of 6 in more depth, consider the following key points:
- Not a Perfect Square: The number 6 is not a perfect square because it cannot be expressed as the product of an integer with itself. Thus, \( \sqrt{6} \) is not an integer.
- Irrational Number: The square root of 6 is an irrational number, which means it cannot be expressed as a simple fraction. Its decimal expansion is non-terminating and non-repeating. The approximate value is: \[ \sqrt{6} \approx 2.449489742783 \]
- Mathematical Representation: In exponential form, the square root of 6 can be written as: \[ \sqrt{6} = 6^{1/2} \]
Let's look at the methods for calculating the square root of 6:
- Using a Calculator: Simply enter 6 and press the square root function (√) to get approximately 2.4495.
- Using Long Division: This traditional method allows for manual calculation of the square root. The steps involve pairing the digits of 6 and iteratively finding the quotient to achieve a more accurate decimal value.
- Using Newton's Method: Also known as the Babylonian method, it iteratively refines guesses for \( \sqrt{6} \): \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{6}{x_n} \right) \] This method converges rapidly to the true value of the square root.
In geometry, \( \sqrt{6} \) appears in various contexts, such as the distance between vertices of certain geometric shapes. For example, in a regular octahedron, the edge length is proportional to \( \sqrt{6} \) times the radius of an inscribed sphere.
In summary, the square root of 6 is a fundamental mathematical concept with applications in various fields, including geometry, algebra, and numerical analysis.
Mathematical Proof of Irrationality
To prove that the square root of 6 is irrational, we can use a method known as proof by contradiction. Let's assume, for the sake of argument, that the square root of 6 is rational. If it is rational, it can be expressed as a fraction a/b, where a and b are integers with no common divisors other than 1, and b ≠ 0.
Given this assumption, we can write:
\( \sqrt{6} = \frac{a}{b} \)
Squaring both sides of the equation, we get:
\( 6 = \frac{a^2}{b^2} \)
\( a^2 = 6b^2 \)
This implies that \(a^2\) is divisible by 6. For \(a^2\) to be divisible by 6, \(a\) itself must be divisible by 6 (since 6 is not a perfect square, and the prime factorization must include all prime factors to an even power). Let \(a = 6k\) for some integer \(k\). Substituting this back into the equation, we get:
\( (6k)^2 = 6b^2 \)
\( 36k^2 = 6b^2 \)
\( 6k^2 = b^2 \)
This implies that \(b^2\) is also divisible by 6, which means \(b\) must be divisible by 6. However, this contradicts our initial assumption that \(a\) and \(b\) have no common divisors other than 1. Hence, our assumption that \(\sqrt{6}\) is rational must be false.
Therefore, the square root of 6 is irrational.

Historical Context and Significance
The concept of irrational numbers has a rich and intriguing history, rooted in ancient Greek mathematics. The discovery of irrational numbers is often attributed to Hippasus of Metapontum, a philosopher of the Pythagorean school. This discovery was revolutionary because it challenged the Pythagorean belief that all numbers could be expressed as the ratio of two integers (rational numbers).
According to legend, Hippasus demonstrated the irrationality of the square root of 2 while trying to find the length of the diagonal of a unit square. This revelation was so controversial that, according to some accounts, it led to his execution by drowning, as it was believed to undermine the foundational principles of Pythagorean philosophy, which held that numbers and their ratios were the basis of all reality.
Despite the initial resistance, the concept of irrational numbers gradually gained acceptance. The work of Euclid, particularly his proof of the irrationality of the square root of 2, provided a more formal foundation for the understanding of irrational numbers. This proof demonstrated that no two integers can exist whose ratio equals the square root of 2, reinforcing the existence of irrational numbers.
The acceptance and understanding of irrational numbers had significant implications for mathematics and science. It led to a more comprehensive number system and paved the way for the development of real numbers. This expanded the scope of mathematical exploration and allowed for a deeper understanding of continuous quantities and geometric properties.
In summary, the discovery of irrational numbers marked a pivotal moment in the history of mathematics, challenging established beliefs and leading to significant advancements in mathematical theory and practice.
Decimal Expansion of Square Root of 6
The decimal expansion of the square root of 6 is a non-terminating and non-repeating decimal, indicative of its irrationality. The square root of 6, approximately 2.449489742783178, can be found through various methods such as the long division method or Newton's method. Below is a detailed explanation of its decimal expansion using the long division method:
- Start with the number 6 and pair the digits from right to left. For 6, it is just 6.00, 60.00, and so on.
- Find the largest number whose square is less than or equal to 6. In this case, it is 2 (since 22 = 4).
- Subtract 4 from 6, giving a remainder of 2. Bring down a pair of zeros, making it 200.
- Double the quotient (2) to get 4, and set it as the new divisor (4X). Find the largest digit X such that 4X × X is less than or equal to 200. Here, X is 4 (since 44 × 4 = 176).
- Subtract 176 from 200, giving a remainder of 24. Bring down the next pair of zeros, making it 2400.
- The next divisor is 44 + 4 = 48. Repeat the process to find the next digit of the quotient.
The process continues, generating more digits of the square root. The first few digits of the decimal expansion of the square root of 6 are:
\[
\sqrt{6} = 2.449489742783178
\]
This non-repeating, non-terminating nature confirms that the square root of 6 is irrational. Here is a table showing the first few steps of the long division method:
| Step | Divisor | Dividend | Quotient | Remainder |
|---|---|---|---|---|
| 1 | 2 | 6.0000 | 2 | 2.0000 |
| 2 | 40 | 200 | 4 | 24 |
| 3 | 484 | 2400 | 4 | 16 |
The decimal expansion of \(\sqrt{6}\) helps in various practical applications, such as in geometry and trigonometry, where precise calculations are crucial.
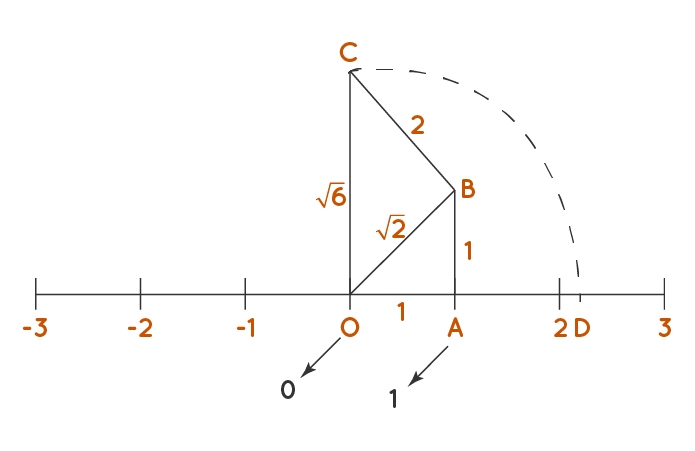
Visual Representation
Visualizing the square root of 6 can enhance our understanding of its properties and significance. One common way to represent square roots is through a number line or a geometric square root spiral.
Number Line Representation
On a number line, the square root of 6 can be approximated to show its position between the integers 2 and 3. Since \( \sqrt{6} \approx 2.449 \), it is slightly less than 2.5. Here's a simple representation:
- Mark the integers 2 and 3 on the number line.
- Place a point slightly to the left of the midpoint between 2 and 3.
- Label this point as \( \sqrt{6} \).
Square Root Spiral
A more artistic and geometric representation is the square root spiral. This spiral is constructed by plotting the square roots of successive integers and connecting them in a spiral pattern.
- Start at the origin (0, 0) on a graph paper.
- Plot the first point at \( (1, \sqrt{1}) \).
- Plot the next point at \( (2, \sqrt{2}) \), and so on.
- For \( \sqrt{6} \), plot the point at \( (6, \sqrt{6}) \).
- Connect these points to form a spiral.
This visual representation not only shows the growth rate of square roots but also highlights their non-linear nature and symmetric properties.
Graphical Representation Using Tools
Tools like Desmos can be used to create a precise visual representation of the square root of 6. By inputting the function \( y = \sqrt{x} \), you can see how \( \sqrt{6} \) fits into the curve.
Visual representations such as these can help in comprehending the non-integer nature of \( \sqrt{6} \) and its position relative to other numbers.
Applications in Mathematics and Science
The square root of 6, although irrational, finds applications across various fields in mathematics and science due to its fundamental properties. Here are some key applications:
-
Pythagorean Theorem:
In geometry, the Pythagorean Theorem is used to find the lengths of sides in right-angled triangles. For instance, if one leg of a right triangle is \( \sqrt{6} \) units and the other leg is 3 units, the hypotenuse can be calculated as:
\[
c = \sqrt{(\sqrt{6})^2 + 3^2} = \sqrt{6 + 9} = \sqrt{15}
\] -
Distance Formula:
The distance between two points in a plane can be calculated using the distance formula, which is derived from the Pythagorean Theorem. For example, the distance between points \((0,0)\) and \((3, \sqrt{6})\) is:
\[
d = \sqrt{(3-0)^2 + (\sqrt{6}-0)^2} = \sqrt{9 + 6} = \sqrt{15}
\] -
Quadratic Equations:
Square roots are crucial in solving quadratic equations using the quadratic formula. For an equation like \(ax^2 + bx + c = 0\), the solutions involve square roots:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\] -
Physics and Engineering:
In physics and engineering, square roots are used in formulas for motion, energy, and waves. For example, the natural frequency of a mass-spring system is given by:
\[
f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]
where \(k\) is the spring constant and \(m\) is the mass. -
Statistics:
Square roots are also used in statistics, such as in calculating standard deviation, which measures the dispersion of a dataset. The formula for standard deviation is:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
\]
where \(N\) is the number of observations, \(x_i\) is each individual observation, and \(\mu\) is the mean.
These examples illustrate how the concept of square roots, including the square root of 6, permeates various disciplines, highlighting its importance and utility.
Common Misconceptions
There are several common misconceptions regarding the square root of 6 and irrational numbers in general. Here, we will address some of the most prevalent misunderstandings:
- Misconception 1: Square roots always yield rational numbers
Many people believe that square roots of natural numbers should always result in rational numbers. However, this is not true. While the square roots of perfect squares (like 4, 9, or 16) are rational, the square roots of non-perfect squares (like 6) are irrational.
- Misconception 2: The square root function always returns two values
There is a common misunderstanding that the square root of a number always yields both positive and negative values. While it's true that the equation \(x^2 = 6\) has two solutions (\(x = \sqrt{6}\) and \(x = -\sqrt{6}\)), the square root function itself, \( \sqrt{x} \), is defined to return only the non-negative root. Thus, \( \sqrt{6} \) refers to the positive value only.
- Misconception 3: Irrational numbers cannot be expressed or understood easily
It is often thought that because irrational numbers have non-repeating, non-terminating decimal expansions, they are somehow less comprehensible or useful. However, irrational numbers are well-defined and crucial in various fields of mathematics and science, even if their decimal expansions are infinite.
- Misconception 4: Any non-integer square root is irrational
Some assume that any square root of a non-integer number must be irrational. While this is true for many cases, it's not a universal rule. For example, the square root of \(\frac{1}{4}\) is \(\frac{1}{2}\), which is rational. However, the square root of 6 is indeed irrational.
Understanding these misconceptions is essential for a clearer grasp of irrational numbers and their properties, particularly when exploring the square root of non-perfect squares such as 6.
Video cung cấp bằng chứng rằng căn bậc hai của bất kỳ số nguyên nào là vô tỷ, ngoại trừ các số chính phương.
Bằng chứng rằng căn bậc hai của BẤT KỲ số nguyên nào là vô tỷ (trừ các số chính phương)
READ MORE:
Video chứng minh rằng căn bậc hai của 6 là một số vô tỷ, giúp người xem hiểu rõ hơn về tính chất của các số vô tỷ.
Chứng minh căn bậc hai của 6 là vô tỷ