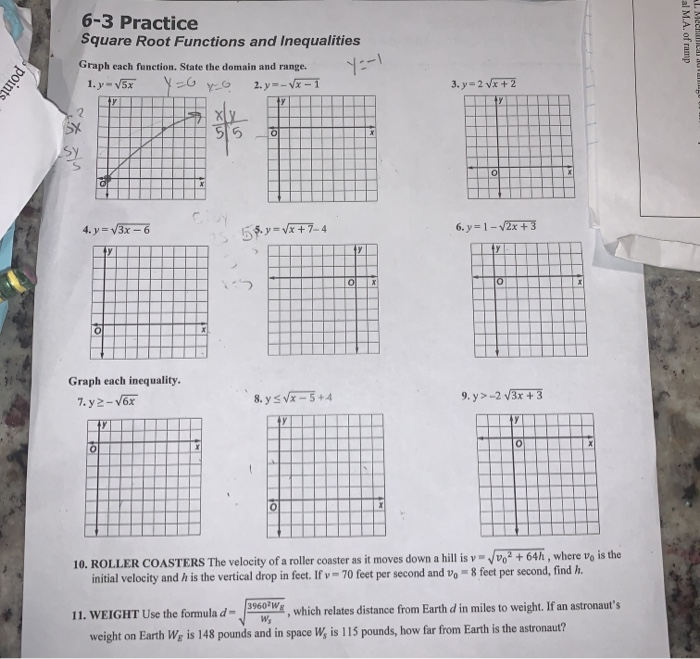
Topic 6-3 practice square root functions and inequalities: Welcome to our comprehensive guide on 6-3 practice for mastering square root functions and inequalities. This article will help you understand the core concepts, learn how to graph and solve equations and inequalities, and apply these skills effectively. Dive in to enhance your mathematical prowess and confidence.
Table of Content
- 6-3 Practice: Square Root Functions and Inequalities
- Introduction to Square Root Functions
- Domain and Range of Square Root Functions
- Transformations of Square Root Functions
- Applications of Square Root Equations
- Applications of Square Root Inequalities
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- YOUTUBE: Khám phá các hàm số căn bậc hai và bất đẳng thức trong video này. Học cách giải và áp dụng trong bài toán thực tế.
6-3 Practice: Square Root Functions and Inequalities
This practice will cover the fundamentals of square root functions and inequalities, focusing on their properties, graphing, and solving related equations and inequalities.
Square Root Functions
A square root function is a function that contains a square root of a variable. It is generally in the form:
\[ f(x) = \sqrt{x - h} + k \]
where \( (h, k) \) is the vertex of the function.
Properties of Square Root Functions
- The domain of \( f(x) = \sqrt{x - h} + k \) is \( x \geq h \).
- The range of \( f(x) = \sqrt{x - h} + k \) is \( y \geq k \).
- The graph of a square root function is a curve that starts at the vertex \( (h, k) \) and increases slowly to the right.
Graphing Square Root Functions
- Identify the vertex \( (h, k) \).
- Determine the domain and range.
- Plot the vertex on the coordinate plane.
- Choose several values of \( x \) greater than \( h \) and calculate the corresponding \( y \) values.
- Plot these points and draw a smooth curve through them, starting at the vertex and moving to the right.
Solving Square Root Equations
To solve equations involving square roots:
- Isolate the square root on one side of the equation.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation.
- Check all solutions in the original equation to ensure they are valid.
Example:
Solve \( \sqrt{2x + 3} = 5 \)
Steps:
- Square both sides: \( (\sqrt{2x + 3})^2 = 5^2 \)
- Result: \( 2x + 3 = 25 \)
- Solve for \( x \): \( 2x = 22 \) → \( x = 11 \)
- Check: \( \sqrt{2(11) + 3} = \sqrt{25} = 5 \) (Valid solution)
Solving Square Root Inequalities
To solve inequalities involving square roots:
- Isolate the square root on one side of the inequality.
- Square both sides to eliminate the square root (be mindful of the direction of the inequality).
- Solve the resulting inequality.
- Check the solutions in the original inequality to ensure they are valid within the domain.
Example:
Solve \( \sqrt{x - 2} \leq 4 \)
Steps:
- Square both sides: \( (\sqrt{x - 2})^2 \leq 4^2 \)
- Result: \( x - 2 \leq 16 \)
- Solve for \( x \): \( x \leq 18 \)
- Check: Ensure \( x - 2 \geq 0 \) (Domain condition) → \( x \geq 2 \)
- Combine conditions: \( 2 \leq x \leq 18 \)
Practice Problems
- Graph the function \( f(x) = \sqrt{x - 1} + 2 \).
- Solve the equation \( \sqrt{3x + 7} = 10 \).
- Solve the inequality \( \sqrt{5 - x} > 1 \).
- Find the domain and range of \( g(x) = \sqrt{2x + 4} - 3 \).
READ MORE:
Introduction to Square Root Functions
Square root functions are functions that involve the square root of a variable. The general form of a square root function is:
\[
f(x) = a\sqrt{x - h} + k
\]
where \( a \), \( h \), and \( k \) are constants.
Key characteristics of square root functions include:
- The domain: The set of all possible input values (x) for which the function is defined. For the function \( f(x) = \sqrt{x} \), the domain is \( x \geq 0 \).
- The range: The set of all possible output values (y) the function can produce. For \( f(x) = \sqrt{x} \), the range is \( y \geq 0 \).
For example, in the function \( f(x) = \sqrt{x - 3} + 2 \):
- The domain is \( x \geq 3 \) because the expression under the square root, \( x - 3 \), must be non-negative.
- The range is \( y \geq 2 \) because the smallest value of the square root function \( \sqrt{x - 3} \) is 0, and when we add 2, the smallest value of \( f(x) \) is 2.
Graphically, square root functions produce a curve that starts at the point \( (h, k) \) and increases gradually to the right. The graph is half of a parabola lying on its side.
To graph a square root function:
- Identify the values of \( h \) and \( k \), which determine the starting point (vertex) of the graph.
- Plot the vertex \((h, k)\).
- Choose a few values of \( x \) greater than \( h \), calculate the corresponding \( y \) values, and plot these points.
- Draw a smooth curve through the points, extending to the right.
Let's consider an example:
Graph the function \( f(x) = 2\sqrt{x - 1} - 3 \).
- Vertex: The function starts at \( (1, -3) \).
- Plot additional points: For \( x = 2 \), \( f(2) = 2\sqrt{2 - 1} - 3 = 2(1) - 3 = -1 \). For \( x = 5 \), \( f(5) = 2\sqrt{5 - 1} - 3 = 2(2) - 3 = 1 \).
The graph starts at (1, -3) and moves upward to the right.
Domain and Range of Square Root Functions
The domain and range of square root functions are crucial to understanding their behavior and graphing them accurately. A square root function has the general form:
\[
f(x) = a\sqrt{x - h} + k
\]
where \( a \), \( h \), and \( k \) are constants.
Domain:
The domain of a square root function consists of all the input values (x) that make the expression under the square root non-negative. This ensures that the function is defined since the square root of a negative number is not real. Mathematically, for the function \( f(x) = \sqrt{x - h} + k \), the domain is determined by setting the radicand (the expression inside the square root) greater than or equal to zero:
\[
x - h \geq 0 \quad \Rightarrow \quad x \geq h
\]
Thus, the domain of \( f(x) = \sqrt{x - h} + k \) is \( x \geq h \).
For example, for the function \( f(x) = \sqrt{x - 3} \), the domain is:
- \( x \geq 3 \)
Range:
The range of a square root function is the set of all possible output values (y). Since a square root function always outputs non-negative values and can be shifted vertically by \( k \), the range is determined by the value of \( k \). For the function \( f(x) = a\sqrt{x - h} + k \), the range is:
\[
y \geq k \quad \text{if} \quad a > 0
\]
\[
y \leq k \quad \text{if} \quad a < 0
\]
For instance, for the function \( f(x) = \sqrt{x - 3} + 2 \), the range is:
- \( y \geq 2 \)
Here are a few more examples:
- For \( f(x) = -\sqrt{x + 4} - 1 \):
- Domain: \( x \geq -4 \)
- Range: \( y \leq -1 \)
- For \( f(x) = 2\sqrt{x - 5} + 3 \):
- Domain: \( x \geq 5 \)
- Range: \( y \geq 3 \)
Understanding the domain and range helps in accurately graphing and analyzing square root functions.
Transformations of Square Root Functions
Transformations of square root functions involve shifting, stretching, compressing, and reflecting the graph of the parent function \( y = \sqrt{x} \). These transformations can be described using the general form of the square root function:
\( y = a \sqrt{b(x - h)} + k \)
Here, a, b, h, and k are constants that determine the type and extent of the transformation:
- Horizontal Shift: The graph shifts horizontally by h units. If h is positive, the shift is to the right; if h is negative, the shift is to the left. This is represented by the term \( (x - h) \).
- Vertical Shift: The graph shifts vertically by k units. If k is positive, the shift is upward; if k is negative, the shift is downward. This is represented by the term \( + k \).
- Reflection: The graph reflects across the x-axis if a is negative. This changes the orientation of the graph.
- Vertical Stretch/Compression: The graph is stretched vertically by a factor of a if \(|a| > 1\), and compressed vertically by a factor of a if \(|a| < 1\). This changes the steepness of the graph.
- Horizontal Stretch/Compression: The graph is compressed horizontally by a factor of b if \(|b| > 1\), and stretched horizontally by a factor of b if \(|b| < 1\). This changes the width of the graph.
Let's explore these transformations with examples:
Examples
Example 1: Horizontal and Vertical Shifts
The function \( y = \sqrt{x - 3} + 2 \) represents the parent function \( y = \sqrt{x} \) shifted 3 units to the right and 2 units upward.
Graphically, this transformation can be visualized as:
\( y = \sqrt{x - 3} + 2 \)
Example 2: Vertical Stretch and Reflection
The function \( y = -2\sqrt{x} \) represents the parent function \( y = \sqrt{x} \) reflected across the x-axis and stretched vertically by a factor of 2.
Graphically, this transformation can be visualized as:
\( y = -2\sqrt{x} \)
Example 3: Horizontal Compression and Vertical Shift
The function \( y = \sqrt{2(x + 1)} - 3 \) represents the parent function \( y = \sqrt{x} \) compressed horizontally by a factor of \(\frac{1}{2}\), shifted 1 unit to the left, and 3 units downward.
Graphically, this transformation can be visualized as:
\( y = \sqrt{2(x + 1)} - 3 \)
Practice Problems
Try to determine the transformations for the following square root functions:
- \( y = \sqrt{x + 4} - 5 \)
- \( y = 3\sqrt{x} + 1 \)
- \( y = \sqrt{0.5(x - 2)} \)
For each function, describe the horizontal shift, vertical shift, reflection, and vertical or horizontal stretching/compression.
Applications of Square Root Equations
Square root equations are used in various real-world applications. Here are some key examples:
1. Physics
In physics, square root functions are often used to describe phenomena such as the speed of an object under certain conditions. For example, the speed of a car before braking can be calculated using the equation:
\[ v = \sqrt{2 \cdot f \cdot d} \]
where \( v \) is the speed, \( f \) is the coefficient of friction, and \( d \) is the distance of the skid marks. This formula helps police determine the speed of vehicles involved in accidents based on the length of skid marks.
2. Engineering
Square root equations are also used in engineering to calculate the strength of materials. For example, the stress (\( \sigma \)) on a material can be determined using the formula:
\[ \sigma = \sqrt{\frac{P}{A}} \]
where \( P \) is the load applied and \( A \) is the cross-sectional area. This helps in designing structures that can withstand specific loads without failing.
3. Finance
In finance, square root equations are used to calculate standard deviation, which is a measure of the volatility or risk of an investment. The formula for the standard deviation (\( \sigma \)) is:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \]
where \( N \) is the number of observations, \( x_i \) represents each individual observation, and \( \mu \) is the mean of the observations. This is crucial for assessing the risk associated with different financial assets.
4. Medicine
In medicine, square root functions are used in pharmacokinetics to determine the concentration of a drug in the bloodstream over time. The equation:
\[ C(t) = C_0 \cdot e^{-kt} \]
where \( C(t) \) is the concentration at time \( t \), \( C_0 \) is the initial concentration, and \( k \) is the elimination rate constant, can be modified with a square root term to model specific conditions of drug absorption and elimination.
5. Biology
In biology, the growth rate of certain populations can be modeled using square root functions. For instance, the growth of bacteria under limited resources can be expressed as:
\[ N(t) = \sqrt{N_0 \cdot t} \]
where \( N(t) \) is the population at time \( t \), and \( N_0 \) is the initial population. This helps in understanding and predicting the dynamics of population growth under varying conditions.
6. Construction
Square root functions are used in construction to determine the height of a structure based on its shadow length. The relationship can be given by:
\[ h = \sqrt{L \cdot \tan(\theta)} \]
where \( h \) is the height, \( L \) is the length of the shadow, and \( \theta \) is the angle of elevation of the sun. This application is particularly useful for ensuring proper sunlight exposure for buildings.
Understanding these applications highlights the importance of square root functions across different fields, providing valuable tools for solving practical problems.

Applications of Square Root Inequalities
Square root inequalities have a wide range of applications in real-world problems. Here are some common scenarios:
- Physics and Engineering:
Square root inequalities are often used to describe physical constraints. For instance, the relationship between the speed of a vehicle and stopping distance can be modeled using square root inequalities.
Example: If \( d \) represents stopping distance and \( v \) represents speed, we might have:
\[ d \leq k\sqrt{v} \]
where \( k \) is a constant depending on road conditions and reaction time.
- Economics:
In economics, square root inequalities can model diminishing returns. For example, the relationship between investment and profit might be represented by:
\[ P \leq c\sqrt{I} \]
where \( P \) is profit, \( I \) is investment, and \( c \) is a constant.
- Biology:
Growth rates in biology, such as the growth of populations or the spread of diseases, can sometimes be expressed with square root inequalities.
Example: The growth of a population \( G \) might be limited by resources, modeled as:
\[ G \leq r\sqrt{R} \]
where \( R \) is the resource availability and \( r \) is a growth rate constant.
Let's consider a specific application example:
- Problem: A roller coaster's velocity \( v \) depends on the height \( h \) of its drop, following \( v = \sqrt{64h} \). Find the maximum height \( h \) if the velocity must not exceed 80 feet per second.
- Solution:
- Set up the inequality: \( \sqrt{64h} \leq 80 \)
- Square both sides: \( 64h \leq 6400 \)
- Solve for \( h \): \( h \leq 100 \)
Thus, the height of the drop must be at most 100 feet.
Common Mistakes and How to Avoid Them
When working with square root functions and inequalities, students often encounter several common mistakes. Here are some of these errors and tips on how to avoid them:
- Incorrectly Simplifying Radicals:
Mistake: Simplifying \( \sqrt{x^2 + y^2} \) as \( x + y \).
Solution: Remember that \( \sqrt{x^2 + y^2} \neq x + y \). Always simplify within the radical before attempting to separate terms.
- Forgetting the Domain Restrictions:
Mistake: Ignoring the fact that square root functions are only defined for non-negative radicands.
Solution: Always set the radicand greater than or equal to zero and solve for the domain first.
Example: For \( f(x) = \sqrt{x - 3} \), solve \( x - 3 \geq 0 \) which gives \( x \geq 3 \).
- Misapplying Transformations:
Mistake: Applying vertical and horizontal shifts incorrectly.
Solution: Follow the correct order of transformations: first handle horizontal shifts, then reflect and stretch/compress, and finally apply vertical shifts.
Example: For \( g(x) = \sqrt{x + 2} - 1 \), shift left by 2 units and down by 1 unit.
- Incorrectly Solving Square Root Equations:
Mistake: Forgetting to square both sides of the equation correctly or neglecting to check for extraneous solutions.
Solution: Always isolate the square root on one side and then square both sides. Check solutions in the original equation.
Example: Solve \( \sqrt{2x + 3} = 5 \):
- Square both sides: \( 2x + 3 = 25 \)
- Solve: \( 2x = 22 \), \( x = 11 \)
- Check: \( \sqrt{2(11) + 3} = 5 \) is valid.
- Mishandling Square Root Inequalities:
Mistake: Not considering both parts of the inequality when squaring.
Solution: Split the inequality into two parts and solve separately. Ensure the solutions satisfy the original inequality.
Example: Solve \( \sqrt{x + 4} \leq 6 \):
- Set up two inequalities: \( x + 4 \geq 0 \) and \( \sqrt{x + 4} \leq 6 \)
- Solve: \( x + 4 \geq 0 \) gives \( x \geq -4 \) and \( x + 4 \leq 36 \) gives \( x \leq 32 \)
- Combine: \( -4 \leq x \leq 32 \)
Practice Problems and Solutions
Here are some practice problems to help reinforce your understanding of square root functions and inequalities. Each problem is followed by a detailed solution.
Problem 1: Solving Square Root Equations
Solve the equation: \( \sqrt{2x + 3} = 5 \)
- Isolate the square root: \( \sqrt{2x + 3} = 5 \)
- Square both sides to eliminate the square root: \( (\sqrt{2x + 3})^2 = 5^2 \)
- Simplify: \( 2x + 3 = 25 \)
- Solve for \( x \): \( 2x = 22 \)
- Divide by 2: \( x = 11 \)
Solution: \( x = 11 \)
Problem 2: Solving Square Root Inequalities
Solve the inequality: \( \sqrt{x + 1} < 3 \)
- Isolate the square root: \( \sqrt{x + 1} < 3 \)
- Square both sides to eliminate the square root: \( (\sqrt{x + 1})^2 < 3^2 \)
- Simplify: \( x + 1 < 9 \)
- Solve for \( x \): \( x < 8 \)
- Consider the domain of the square root: \( x + 1 \geq 0 \Rightarrow x \geq -1 \)
- Combine the results: \( -1 \leq x < 8 \)
Solution: \( -1 \leq x < 8 \)
Problem 3: Application of Square Root Functions
The height \( h \) (in feet) of a falling object after \( t \) seconds is given by the equation \( h = 100 - 16t^2 \). At what time will the object hit the ground?
- Set the height to zero: \( 100 - 16t^2 = 0 \)
- Solve for \( t^2 \): \( 16t^2 = 100 \)
- Divide by 16: \( t^2 = \frac{100}{16} \)
- Simplify: \( t^2 = 6.25 \)
- Take the square root of both sides: \( t = \sqrt{6.25} \)
- Simplify: \( t = 2.5 \)
Solution: The object will hit the ground after 2.5 seconds.
Problem 4: Graphing Square Root Functions
Graph the function \( y = \sqrt{x - 2} \) and identify the domain and range.
- Determine the domain: \( x - 2 \geq 0 \Rightarrow x \geq 2 \)
- Calculate points for the graph:
- When \( x = 2 \), \( y = \sqrt{2 - 2} = 0 \)
- When \( x = 3 \), \( y = \sqrt{3 - 2} = 1 \)
- When \( x = 6 \), \( y = \sqrt{6 - 2} = 2 \)
- Plot the points and draw the curve starting from \( (2, 0) \).
Domain: \( x \geq 2 \)
Range: \( y \geq 0 \)
Khám phá các hàm số căn bậc hai và bất đẳng thức trong video này. Học cách giải và áp dụng trong bài toán thực tế.
6-3 Hàm số căn bậc hai và Bất đẳng thức
READ MORE:
Khám phá hàm số căn bậc hai và bất đẳng thức trong bài học Đại số 2 này. Học cách giải và áp dụng vào các bài toán thực tế.
Bài học Đại số 2: Hàm số căn bậc hai và Bất đẳng thức