Topic square root of 6 simplified: The square root of 6 simplified is an essential concept in mathematics, helping students and enthusiasts grasp the properties of irrational numbers. This guide offers clear, step-by-step instructions to simplify the square root of 6, understand its mathematical significance, and explore its applications in various fields. Dive in to simplify and appreciate this intriguing number!
Table of Content
- Square Root of 6 Simplified
- Introduction to Square Roots
- Understanding the Square Root of 6
- Prime Factorization Method
- Steps to Simplify Square Roots
- Why the Square Root of 6 is Irrational
- Decimal Approximation of the Square Root of 6
- Mathematical Properties of the Square Root of 6
- Applications in Geometry
- Applications in Algebra
- Comparing Square Roots of Different Numbers
- Common Misconceptions
- Conclusion
- YOUTUBE:
Square Root of 6 Simplified
The square root of 6 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. To simplify the square root of 6, we look for perfect square factors of 6.
Steps to Simplify the Square Root of 6
- Identify the factors of 6. The factors are 1, 2, 3, and 6.
- Check if any of these factors are perfect squares. In this case, none of them are perfect squares (1 is a trivial perfect square).
- Since 6 has no perfect square factors (other than 1), the square root of 6 cannot be simplified further using integer factors.
Thus, the simplified form of the square root of 6 remains:
Approximate Value
While the square root of 6 cannot be simplified into a simpler radical form, its approximate decimal value is:
Use in Mathematics
The square root of 6 appears in various mathematical contexts, including geometry and algebra. For example, it might be used in calculations involving right triangles, where the length of a side might be expressed in terms of the square root of 6.
Understanding the properties of irrational numbers like the square root of 6 is crucial in higher mathematics and helps build a strong foundation for advanced mathematical concepts.

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a number that, when multiplied by itself, equals the given value. The square root of a number \( x \) is denoted as \( \sqrt{x} \) or \( x^{1/2} \).
For example:
- The square root of 4 is 2, because \( 2 \times 2 = 4 \).
- The square root of 9 is 3, because \( 3 \times 3 = 9 \).
Square roots can be either positive or negative, but by convention, the principal square root is the non-negative root. For instance:
- The principal square root of 16 is 4, although -4 is also a square root of 16 because \( (-4) \times (-4) = 16 \).
Not all numbers have integer square roots. For example, 2, 3, and 5 do not have exact integer square roots. These are called irrational numbers. Their square roots are non-repeating, non-terminating decimals.
To simplify the square root of a number, follow these steps:
- Factor the number into its prime factors.
- Pair the prime factors.
- Move each pair of factors outside the square root.
- Multiply the factors outside the square root.
- Leave any remaining factors inside the square root.
Square roots are used in various mathematical contexts, including algebra, geometry, and calculus. Understanding how to work with square roots is essential for solving quadratic equations, working with geometric shapes, and analyzing scientific data.
Understanding the Square Root of 6
The square root of 6 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating. Understanding this square root involves recognizing its properties and how it fits into the broader category of irrational numbers.
Here's a step-by-step breakdown:
-
Prime Factorization:
First, we factorize 6 into its prime factors: \( 6 = 2 \times 3 \).
-
Check for Perfect Squares:
We look for perfect square factors. Neither 2 nor 3 are perfect squares.
-
Conclusion:
Since there are no perfect square factors, the square root of 6 cannot be simplified further. It remains in its radical form:
The decimal approximation of the square root of 6 is:
This value is useful in various mathematical calculations, especially in fields requiring precise measurements and computations.
Understanding the square root of 6 also helps in solving equations where this value might appear, and in geometry, where lengths and distances often involve such irrational numbers.
Prime Factorization Method
The prime factorization method is a systematic way to break down a number into its prime factors, which can help simplify square roots. Here’s how you can use this method to understand the square root of 6.
-
Identify the Number:
Start with the number you want to simplify the square root of. In this case, it’s 6.
-
Find Prime Factors:
Determine the prime factors of 6. A prime number is a number greater than 1 that has no positive divisors other than 1 and itself. The prime factors of 6 are:
-
Express in Square Root Form:
Express the square root of 6 in terms of its prime factors:
-
Simplify if Possible:
Check if any of the factors are perfect squares. In this case, neither 2 nor 3 are perfect squares, so they remain inside the square root:
-
Conclusion:
Since there are no perfect square factors to simplify further, the square root of 6 remains:
Using the prime factorization method is a valuable tool in simplifying square roots and understanding the composition of numbers. It is especially useful when dealing with larger numbers and helps identify opportunities to simplify the expression.
Steps to Simplify Square Roots
Simplifying square roots involves breaking down the number inside the square root into its prime factors and then simplifying if possible. Here are the steps to simplify square roots:
-
Factor the Number:
Find the prime factorization of the number under the square root. For example, for 6:
-
Group the Factors:
Group the factors into pairs of identical numbers. Since 6 = 2 × 3, there are no pairs.
-
Simplify the Pairs:
For each pair, take one number out of the square root. Since there are no pairs in the factorization of 6, this step does not apply.
-
Rewrite the Expression:
Write the simplified expression. If no pairs were found, the square root remains the same. For 6:
-
Verify the Result:
Double-check the factors to ensure the square root is simplified correctly. The square root of 6 cannot be simplified further, so it remains:
These steps can be applied to any number to simplify its square root, making calculations easier and helping to understand the properties of numbers more deeply.

Why the Square Root of 6 is Irrational
An irrational number is a number that cannot be expressed as a simple fraction (ratio) of two integers. The square root of 6 is considered irrational because it meets this criterion. Here’s why:
-
Prime Factorization:
First, factorize 6 into its prime factors:
-
No Perfect Squares:
Check for perfect square factors. The factors of 6 (2 and 3) are not perfect squares, which means the square root of 6 cannot be simplified to a rational number.
-
Decimal Representation:
The decimal representation of the square root of 6 is non-terminating and non-repeating, typical characteristics of irrational numbers:
-
Proof by Contradiction:
To formally prove that \( \sqrt{6} \) is irrational, assume the opposite: that it is rational and can be written as a fraction \( \frac{a}{b} \), where a and b are coprime integers. Then:
This implies that \( a^2 \) is a multiple of 6, so a must also be a multiple of 6 (since the square of a non-multiple of 6 cannot be a multiple of 6). Let \( a = 6k \). Substituting, we get:
This shows that \( b^2 \) is also a multiple of 6, meaning b must be a multiple of 6. But this contradicts the assumption that a and b are coprime (they have no common factors other than 1). Thus, the assumption that \( \sqrt{6} \) is rational is false, proving it is irrational.
Understanding why the square root of 6 is irrational helps in recognizing the nature of numbers and their classifications, which is fundamental in various mathematical applications and theories.
Decimal Approximation of the Square Root of 6
The square root of 6 is an irrational number, meaning its decimal representation is non-terminating and non-repeating. To work with this number in practical applications, we often use a decimal approximation. Here’s a detailed look at how to approximate the square root of 6 and its significance:
-
Initial Approximation:
Using a calculator, the square root of 6 can be approximated as:
-
Steps for Manual Approximation:
For a more precise manual calculation, consider the following steps:
- Start with an initial guess. For example, 2.4, because \( 2.4^2 = 5.76 \), which is close to 6.
- Use the method of averaging. Calculate the average of the guess and the result of dividing 6 by the guess:
- Repeat the process to refine the approximation. For the second iteration:
-
Usage of Decimal Approximation:
The decimal approximation is used in various practical applications, such as engineering, physics, and everyday calculations, where an exact value of the square root is not necessary.
-
Significance:
Having a decimal approximation helps in making precise calculations and understanding the magnitude of the square root of 6 in comparison to other numbers.
Overall, while the exact value of the square root of 6 is irrational and complex, its decimal approximation allows for practical usage in calculations and problem-solving.
Mathematical Properties of the Square Root of 6
The square root of 6, represented as \( \sqrt{6} \), possesses several interesting mathematical properties. Understanding these properties can provide deeper insight into its behavior and applications in various fields.
-
Irrationality:
As discussed, \( \sqrt{6} \) is an irrational number. This means it cannot be expressed as a simple fraction of two integers and its decimal representation is non-terminating and non-repeating.
-
Prime Factorization:
The number 6 can be broken down into prime factors:
Since neither of these factors are perfect squares, \( \sqrt{6} \) cannot be simplified further and remains in its radical form.
-
Commutative Property:
The square root function is commutative for multiplication, meaning:
Applying this to \( \sqrt{6} \):
-
Approximation:
The decimal approximation of \( \sqrt{6} \) is:
This approximation is useful for practical calculations where exact precision is not required.
-
Exponential Form:
In exponential notation, \( \sqrt{6} \) can be written as:
This form is particularly useful in algebraic manipulations and calculus.
-
Algebraic Equations:
In solving algebraic equations, \( \sqrt{6} \) often appears in quadratic equations and other polynomial equations. For example:
Solving for x in the equation:
These properties highlight the importance and versatility of \( \sqrt{6} \) in various mathematical contexts, from simple calculations to complex equations and theoretical applications.
Applications in Geometry
The square root of 6 (\(\sqrt{6}\)) finds applications in various geometric contexts. Here are some key examples:
-
Diagonal of a Rectangle
Consider a rectangle with sides of lengths 2 and 3. The diagonal (d) can be calculated using the Pythagorean theorem:
\[ d = \sqrt{a^2 + b^2} \]
Substituting the given values:
\[ d = \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \]
While this example uses specific values, the concept can be generalized for any rectangle where the diagonal is often an irrational number involving square roots.
-
Equilateral Triangles
In an equilateral triangle with side length \(s\), the height (h) can be determined using the formula:
\[ h = \frac{\sqrt{3}}{2} s \]
For an equilateral triangle with side length 6:
\[ h = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \]
Here, the height involves the square root of 3, illustrating how square roots appear in standard geometric shapes.
-
Right Triangles and Trigonometry
In right triangles, the square root of 6 can appear as the length of sides or hypotenuses. For example, if one leg (a) of a right triangle is 1 and the hypotenuse (c) is \(\sqrt{6}\), the other leg (b) can be found as:
\[ c^2 = a^2 + b^2 \]
Substituting the values:
\[ (\sqrt{6})^2 = 1^2 + b^2 \]
\[ 6 = 1 + b^2 \]
\[ b^2 = 5 \]
\[ b = \sqrt{5} \]
-
Circle and Arc Lengths
In circles, the relationship between the radius (r), diameter (d), and circumference (C) often involves square roots when dealing with arcs and sectors. For example, the length of an arc (L) with a central angle \(\theta\) in radians and radius \(\sqrt{6}\) is:
\[ L = r \theta \]
For a central angle of \(\pi/3\):
\[ L = \sqrt{6} \times \frac{\pi}{3} = \frac{\pi \sqrt{6}}{3} \]
These examples demonstrate how square roots, including \(\sqrt{6}\), are integral to solving various geometric problems, highlighting their importance in mathematics and practical applications.

Applications in Algebra
The square root of 6 (\(\sqrt{6}\)) has various applications in algebra, from solving equations to simplifying expressions. Here are some key applications:
- Simplifying Expressions:
In algebra, we often need to simplify expressions involving square roots. For example, an expression like \(\sqrt{24}\) can be simplified by breaking it down into its prime factors: \(\sqrt{24} = \sqrt{4 \times 6} = \sqrt{4} \times \sqrt{6} = 2\sqrt{6}\).
- Solving Quadratic Equations:
Quadratic equations sometimes involve the square root of non-perfect squares. For instance, solving the equation \(x^2 - 6 = 0\) requires finding the square roots of 6: \(x = \pm \sqrt{6}\).
- Radical Expressions:
Expressions involving radicals can be simplified using properties of square roots. For example, \(\sqrt{a} \times \sqrt{b} = \sqrt{ab}\). So, \(\sqrt{2} \times \sqrt{3} = \sqrt{6}\).
- Rationalizing the Denominator:
When dealing with fractions, it's often useful to rationalize the denominator. For example, \(\frac{1}{\sqrt{6}}\) can be rationalized by multiplying the numerator and the denominator by \(\sqrt{6}\), resulting in \(\frac{\sqrt{6}}{6}\).
- Inequalities:
Square roots appear in inequalities. For example, solving \(x^2 < 6\) involves determining the values of \(x\) that make the inequality true: \(-\sqrt{6} < x < \sqrt{6}\).
By understanding these applications, students can better grasp the role of square roots in algebraic processes, making it easier to solve complex problems and understand deeper mathematical concepts.
Comparing Square Roots of Different Numbers
Comparing square roots of different numbers is an essential skill in mathematics, allowing us to understand the relationships between various numerical values and their roots. Here, we will explore the comparison of square roots using examples and techniques for simplification.
Basic Comparisons:
To compare the square roots of different numbers, consider their approximate decimal values. For example:
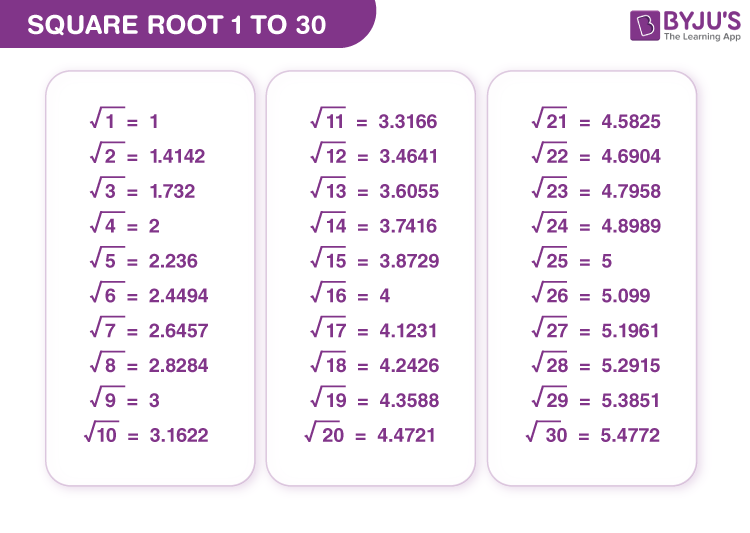
- \(\sqrt{6} \approx 2.449\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
From these values, it is clear that \(\sqrt{4} < \sqrt{6} < \sqrt{9}\).
Simplification for Comparison:
Some square roots can be simplified to make comparisons easier. For instance:
- \(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \approx 2 \times 1.414 = 2.828\)
- \(\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3} \approx 2 \times 1.732 = 3.464\)
Here, \(\sqrt{8} \approx 2.828\) and \(\sqrt{12} \approx 3.464\), indicating that \(\sqrt{8} < \sqrt{12}\).
Using Rational Approximations:
Square roots that are not perfect squares can be approximated using fractions for easier comparison. For example:
- \(\sqrt{2} \approx \frac{3}{2} \approx 1.5\)
- \(\sqrt{3} \approx \frac{7}{4} \approx 1.75\)
Thus, \(\sqrt{2} < \sqrt{3}\).
Comparing Perfect Squares:
Perfect squares have exact roots, making comparison straightforward:
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
Clearly, \(\sqrt{25} < \sqrt{36}\).
Example Table:
| Number | Square Root | Approximate Value |
|---|---|---|
| 6 | \(\sqrt{6}\) | 2.449 |
| 8 | \(\sqrt{8}\) | 2.828 |
| 12 | \(\sqrt{12}\) | 3.464 |
| 25 | \(\sqrt{25}\) | 5 |
Through these methods, comparing square roots becomes a manageable task, whether through simplification, approximation, or direct calculation of perfect squares. This understanding is crucial for more advanced mathematical applications and problem-solving.
Common Misconceptions
Understanding the square root of 6 and other square roots can sometimes lead to misconceptions. Here are some of the most common ones:
- Distributing the Square Root: A common mistake is to think that the square root of a sum is the sum of the square roots. For example, assuming \(\sqrt{a^2 + b^2} = a + b\) is incorrect. The correct form is \(\sqrt{a^2 + b^2}\), which is not equal to \(a + b\).
- Product Instead of Addition: Another frequent error is using multiplication instead of addition in the Pythagorean theorem. For instance, assuming \(c = \sqrt{ab}\) instead of using \(c^2 = a^2 + b^2\) for right triangles.
- Rationalizing Incorrectly: When rationalizing the denominator, students might incorrectly cancel out terms. For example, \(\frac{1}{\sqrt{6}}\) should be rationalized as \(\frac{\sqrt{6}}{6}\), not just \(\frac{1}{6}\).
- Misunderstanding Simplification: Some think that simplifying \(\sqrt{ab}\) is as simple as splitting it into \(\sqrt{a} \cdot \sqrt{b}\). While this is true, it only holds when \(a\) and \(b\) are positive. Simplification requires identifying perfect squares within the radicand.
- Assuming All Square Roots are Rational: Not all square roots are rational numbers. For example, the square root of 6 is irrational and cannot be expressed as a fraction. This is a critical point to remember when dealing with non-perfect squares.
- Ignoring Negative Solutions: When solving equations involving square roots, students often forget the negative root. For example, solving \(x^2 = 6\) yields \(x = \pm \sqrt{6}\), accounting for both positive and negative roots.
By being aware of these common misconceptions, students can approach problems involving square roots more accurately and confidently.
Conclusion
The square root of 6, denoted as \(\sqrt{6}\), is an irrational number approximately equal to 2.449. Understanding its properties and simplification can be achieved through various methods such as prime factorization and approximation techniques.
To simplify \(\sqrt{6}\), we recognize that 6 can be expressed as the product of its prime factors: 2 and 3. Therefore,
\(\sqrt{6} = \sqrt{2 \times 3} = \sqrt{2} \times \sqrt{3}\)
Using the approximate values \(\sqrt{2} \approx 1.414\) and \(\sqrt{3} \approx 1.732\), we can estimate:
\(\sqrt{6} \approx 1.414 \times 1.732 \approx 2.449\)
This simplified form demonstrates how \(\sqrt{6}\) can be broken down into more manageable components for calculations and understanding.
Throughout various mathematical contexts, the square root of 6 finds applications in algebra, geometry, and higher-level mathematics. For example, in algebra, \(\sqrt{6}\) may appear in solutions to quadratic equations or in expressions involving radical simplification. In geometry, it can describe the lengths of diagonals in certain shapes or relate to the Pythagorean theorem in specific scenarios.
One key takeaway is that while \(\sqrt{6}\) is an irrational number and cannot be precisely represented as a simple fraction, it remains a crucial element in mathematical expressions and calculations. Its approximate value allows for practical applications in both theoretical and applied mathematics.
In summary, understanding the square root of 6 involves recognizing its irrational nature, simplifying it through factorization, and appreciating its role across various mathematical disciplines. The journey from recognizing its prime factors to applying its approximate value showcases the interconnectedness of different mathematical concepts and their real-world relevance.
Căn bậc hai của 6