Topic square root of 6 squared: Discover the straightforward yet fascinating calculation of the square root of 6 squared. This article will break down the math, clarify common misconceptions, and reveal the elegance of this mathematical concept. Perfect for students, educators, and math enthusiasts, join us as we explore the simplicity and beauty behind this calculation.
Table of Content
- Understanding the Calculation: Square Root of 6 Squared
- Introduction
- Basic Concepts
- Definition of Square Root
- Understanding Squaring a Number
- Mathematical Expression: Square Root of 6 Squared
- Properties of Square Roots and Squares
- Inverse Operations: Squaring and Square Rooting
- Practical Applications
- Common Mistakes to Avoid
- Advanced Mathematical Insights
- Real-World Examples
- Conclusion
- YOUTUBE: Xem video để hiểu rõ hơn về khái niệm căn bậc hai và cách áp dụng nó trong bài toán căn bậc hai của 6 bình phương.
Understanding the Calculation: Square Root of 6 Squared
The expression we are examining is the square root of 6 squared. Let's break it down step by step using mathematical notation.
Step-by-Step Calculation
- First, we identify the expression: \(\sqrt{6^2}\)
- Next, we calculate the square of 6: \(6^2 = 36\)
- Then, we take the square root of 36: \(\sqrt{36} = 6\)
Therefore, the square root of 6 squared is simply:
\[\sqrt{6^2} = 6\]
Key Points to Remember
- Squaring a number and then taking the square root of the result returns the original number. This is because squaring and square rooting are inverse operations.
- Mathematically, \(\sqrt{a^2} = a\) for any positive number \(a\).
In conclusion, the calculation shows that the square root of 6 squared results in the original number, 6.

READ MORE:
Introduction
The square root of 6 squared is a basic yet intriguing mathematical concept that often appears in various fields of study. Understanding this concept helps reinforce foundational arithmetic skills and highlights the relationship between squaring a number and finding its square root. In this section, we will explore the calculation and its significance step by step.
To begin, let's define the expression:
\[\sqrt{6^2}\]
- Identify the Expression: The expression is the square root of 6 squared, written as \(\sqrt{6^2}\).
- Calculate the Square: First, we square the number 6:
\[6^2 = 36\]
- Find the Square Root: Next, we take the square root of the result:
\[\sqrt{36} = 6\]
The result demonstrates a fundamental property of square roots and squares: squaring a number and then taking the square root of that result returns the original number. This relationship is a key concept in arithmetic and algebra, emphasizing the inverse nature of these operations.
By understanding and mastering this calculation, one can better appreciate the simplicity and elegance of mathematical principles. This concept not only solidifies basic math skills but also serves as a stepping stone to more advanced topics in mathematics.
Basic Concepts
To understand the square root of 6 squared, it is essential to grasp some basic mathematical concepts: square roots and squaring a number. These fundamental operations form the foundation of this calculation.
Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol \(\sqrt{}\). For example:
\[\sqrt{9} = 3\]
since \(3 \times 3 = 9\).
Squaring a Number
Squaring a number involves multiplying that number by itself. This operation is represented by raising the number to the power of 2. For instance:
\[6^2 = 6 \times 6 = 36\]
Combining the Concepts
When we combine these two operations—squaring a number and then taking the square root of the result—we perform the following steps:
- Square the Number: Calculate \(6^2\):
\[6^2 = 36\]
- Take the Square Root: Find the square root of 36:
\[\sqrt{36} = 6\]
This process highlights a key property in mathematics: the square root and the squaring operations are inverse operations. Thus, when you square a number and then take the square root of the result, you return to the original number.
Understanding these basic concepts is crucial for grasping more complex mathematical ideas and for solving a wide range of mathematical problems. The elegance and simplicity of these operations showcase the beauty of mathematics and its logical structure.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the fundamental operations in mathematics, represented by the radical symbol \(\sqrt{}\). The concept of square roots is crucial for understanding various mathematical principles and solving equations.
Mathematically, the square root of a number \(a\) is written as \(\sqrt{a}\). This can be expressed as:
\[\sqrt{a} = b \quad \text{if and only if} \quad b \times b = a\]
where \(b\) is the square root of \(a\). For example, consider the number 9:
\[\sqrt{9} = 3 \quad \text{because} \quad 3 \times 3 = 9\]
In this case, 3 is the square root of 9. Similarly, the square root of 16 is 4 because:
\[\sqrt{16} = 4 \quad \text{since} \quad 4 \times 4 = 16\]
Positive and Negative Roots
It is important to note that every positive number actually has two square roots: a positive and a negative one. This is because both a positive number and its negative counterpart, when squared, yield the same result:
\[\sqrt{16} = 4 \quad \text{and} \quad \sqrt{16} = -4\]
Both \(4\) and \(-4\) satisfy the equation \(b \times b = 16\). However, by convention, when we refer to "the square root," we typically mean the principal (positive) square root.
Square Root of Perfect Squares
A perfect square is a number that is the square of an integer. For instance, 1, 4, 9, 16, and 25 are perfect squares. The square roots of perfect squares are always integers. For example:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
Square Root of Non-Perfect Squares
For numbers that are not perfect squares, the square root is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating. For example:
\[\sqrt{2} \approx 1.414\]
Understanding the definition of square roots and their properties helps build a solid foundation for more advanced mathematical topics and problem-solving techniques. This knowledge is essential for anyone studying mathematics or related fields.
Understanding Squaring a Number
Squaring a number is a fundamental mathematical operation that involves multiplying the number by itself. This process is essential for various mathematical calculations and concepts. In this section, we will explore the definition, properties, and examples of squaring a number.
Definition of Squaring
When you square a number, you raise it to the power of 2. Mathematically, squaring a number \(a\) is written as \(a^2\). This can be expressed as:
\[a^2 = a \times a\]
For example, squaring the number 6 is calculated as follows:
\[6^2 = 6 \times 6 = 36\]
Properties of Squaring
Squaring a number has several important properties:
- Non-Negativity: The result of squaring any real number is always non-negative. This is because the product of two positive numbers or two negative numbers is always positive.
- Monotonicity: For any two positive numbers \(a\) and \(b\), if \(a < b\), then \(a^2 < b^2\). This property helps in comparing squared values.
- Even Power: Squaring is an even power operation, meaning \(a^2\) is always an even power of \(a\).
Examples of Squaring
To better understand squaring, let's look at a few more examples:
- \(3^2 = 3 \times 3 = 9\)
- \(4^2 = 4 \times 4 = 16\)
- \(5^2 = 5 \times 5 = 25\)
- \(7^2 = 7 \times 7 = 49\)
These examples show how squaring a number results in the product of the number with itself.
Applications of Squaring
Squaring a number is used in various mathematical and real-world applications, including:
- Geometry: Calculating the area of a square, where the side length is squared.
- Physics: Computing energy and force, often involving squared terms.
- Statistics: Determining variance, which involves squaring deviations from the mean.
- Finance: Calculating compound interest, which can involve squared growth rates.
Understanding the concept and properties of squaring a number is crucial for solving mathematical problems and applying mathematical principles in various fields. This fundamental operation lays the groundwork for more complex calculations and theories.

Mathematical Expression: Square Root of 6 Squared
The expression "square root of 6 squared" combines two fundamental mathematical operations: squaring a number and then taking the square root of the result. To understand this expression step by step, let's break down the process.
Step-by-Step Calculation
- Identify the Expression: The expression is \(\sqrt{6^2}\).
- Calculate the Square: First, we square the number 6:
\[6^2 = 6 \times 6 = 36\]
- Take the Square Root: Next, we find the square root of 36:
\[\sqrt{36} = 6\]
Thus, the square root of 6 squared simplifies to 6:
\[\sqrt{6^2} = 6\]
Understanding the Process
This calculation illustrates an important property of square roots and squares: they are inverse operations. Specifically, squaring a number and then taking the square root of the result returns the original number. This can be expressed more generally as:
\[\sqrt{a^2} = a\]
for any non-negative number \(a\). This property is crucial in various areas of mathematics, including algebra, calculus, and geometry.
Visualizing the Concept
To better understand the concept, consider a geometric interpretation. When we square a number, we are calculating the area of a square with sides of that length. For example, squaring 6 gives us the area of a square with sides of 6 units:
- Side length = 6 units
- Area = \(6^2 = 36\) square units
Taking the square root of the area (36 square units) gives us the original side length:
\[\sqrt{36} = 6\]
This geometric perspective reinforces the relationship between squaring and square rooting as inverse operations.
Conclusion
The expression \(\sqrt{6^2}\) demonstrates the elegant interplay between squaring a number and taking its square root. By understanding this relationship, we gain a deeper appreciation for the fundamental principles of mathematics and their applications in various fields.
Properties of Square Roots and Squares
Understanding the properties of square roots and squares is essential for grasping various mathematical concepts and solving problems effectively. These properties highlight the unique relationships and characteristics of squaring a number and taking its square root.
Properties of Squares
When a number is squared, it is multiplied by itself. Here are some key properties of squares:
- Non-Negativity: The square of any real number is always non-negative. For any real number \(a\):
\[a^2 \geq 0\]
This is because both positive and negative numbers, when squared, yield a positive result (or zero in the case of zero).
- Monotonicity: Squaring is a monotonic function for non-negative numbers, meaning that if \(a \leq b\), then \(a^2 \leq b^2\). This property helps in comparing squared values.
- Even Power: Squaring is an even power operation, and the result of squaring a number is always an even power of that number.
- Area Representation: Geometrically, the square of a number can represent the area of a square with sides of that length. For instance, \(6^2\) represents the area of a square with side lengths of 6 units.
Properties of Square Roots
Square roots are the inverse operation of squaring a number. Key properties of square roots include:
- Non-Negativity: The square root of a non-negative number is always non-negative. For any non-negative number \(a\):
\[\sqrt{a} \geq 0\]
- Inverse Operation: The square root and the squaring operations are inverse functions. This means that for any non-negative number \(a\):
\[\sqrt{a^2} = a \quad \text{and} \quad (\sqrt{a})^2 = a\]
- Product Property: The square root of a product is the product of the square roots of the factors. For any non-negative numbers \(a\) and \(b\):
\[\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\]
- Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. For any non-negative numbers \(a\) and \(b\) (with \(b \neq 0\)):
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
- Simplification: The square root of a perfect square (an integer that is the square of another integer) is always an integer. For example:
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
Interrelation of Square Roots and Squares
The interrelation between square roots and squares is evident in their properties as inverse operations. This interrelation can be summarized as follows:
- Squaring a number and then taking the square root of the result returns the original number:
\[\sqrt{6^2} = 6\]
- Taking the square root of a number and then squaring the result also returns the original number:
\[(\sqrt{36})^2 = 36\]
These properties illustrate the fundamental nature of these operations in mathematics. Understanding these relationships enhances our ability to solve equations, simplify expressions, and appreciate the logical structure of mathematical concepts.
Inverse Operations: Squaring and Square Rooting
Understanding the relationship between squaring a number and taking its square root is essential in mathematics. These two operations are inverse processes, meaning one operation undoes the effect of the other. Let's explore this concept in detail.
Squaring a Number
Squaring a number means multiplying the number by itself. The mathematical notation for squaring a number \( x \) is \( x^2 \). For example, squaring the number 6 is written as:
\[ 6^2 = 6 \times 6 = 36 \]
Square Root of a Number
Taking the square root of a number is the inverse operation of squaring. The square root of a number \( y \) is a value \( x \) such that when \( x \) is squared, it equals \( y \). The notation for the square root of \( y \) is \( \sqrt{y} \). For example, the square root of 36 is written as:
\[ \sqrt{36} = 6 \]
Inverse Relationship
The operations of squaring and taking the square root are inverses of each other. This means that for any positive number \( x \):
\[ \sqrt{x^2} = x \]
\[ (\sqrt{x})^2 = x \]
Example: Square Root of 6 Squared
Let's apply these concepts to the specific example of the square root of 6 squared. First, we square the number 6:
\[ 6^2 = 36 \]
Then, we take the square root of the result:
\[ \sqrt{36} = 6 \]
Therefore, the square root of 6 squared is 6:
\[ \sqrt{6^2} = 6 \]
Visual Representation
| Operation | Expression | Result |
| Squaring | \( 6^2 \) | 36 |
| Square Root | \( \sqrt{36} \) | 6 |
| Combined | \( \sqrt{6^2} \) | 6 |
Key Points to Remember
- Squaring a number means multiplying it by itself.
- Taking the square root of a number finds a value that, when squared, equals the original number.
- Squaring and square rooting are inverse operations.
- The square root of a squared number returns the original number.
Conclusion
In summary, understanding the inverse relationship between squaring a number and taking its square root is fundamental in mathematics. This relationship helps simplify many mathematical problems and is widely used in various applications.
Practical Applications
Understanding the square root of a number and the process of squaring is not just a theoretical exercise; these concepts have numerous practical applications in various fields. Below are some key areas where these mathematical operations are applied:
-
Geometry and Architecture
In geometry, calculating the area of squares and determining the length of sides often requires understanding squares and square roots. For instance, if you know the area of a square, you can find the length of one side by taking the square root of the area. This principle is crucial in architecture and construction when planning layouts and ensuring structural integrity.
-
Physics
In physics, squares and square roots are used to calculate various properties such as velocity, acceleration, and force. For example, the distance formula in kinematics, which is derived from the Pythagorean theorem, involves square roots to determine the resultant distance between two points.
-
Finance
Square roots are used in various financial formulas, including those for calculating compound interest and assessing risk in investments. The standard deviation, a measure of investment risk, is derived using the square root of the variance, highlighting the importance of these operations in financial analysis.
-
Statistics and Data Analysis
In statistics, squaring and square roots are fundamental in calculating variance and standard deviation, which help in understanding the spread and consistency of data. These measures are crucial for data analysis, enabling statisticians to make sense of data distributions.
-
Computer Graphics and Game Development
Square roots are essential in computer graphics and game development for calculating distances in 2D and 3D spaces. The distance formula, which uses square roots, is critical for rendering accurate visuals and creating realistic animations.
These examples illustrate the wide range of applications for squaring and square roots, from academic subjects to everyday practical tasks. Understanding these concepts opens up a world of problem-solving possibilities.

Common Mistakes to Avoid
When working with square roots and squaring numbers, it is easy to make mistakes that can lead to incorrect results. Here are some common errors and tips on how to avoid them:
- Confusing Squares and Square Roots: Remember that squaring a number and taking the square root are inverse operations. Squaring a number means multiplying it by itself, while taking the square root of a number finds a value that, when squared, equals the original number. For example, \(6^2 = 36\) and \(\sqrt{36} = 6\).
- Incorrectly Applying Square Root to Negative Numbers: The square root of a negative number is not defined in the set of real numbers. For example, \(\sqrt{-25}\) is not a real number. Make sure you are working within the correct number set.
- Overlooking the Importance of Parentheses: In mathematical expressions, parentheses are crucial for determining the correct order of operations. For instance, \(\sqrt{6^2}\) is different from \((\sqrt{6})^2\). The former equals 6, while the latter simplifies to 6 as well.
- Misinterpreting the Radical Sign for Only Positive Roots: The square root symbol (√) typically refers to the principal (non-negative) root. However, when solving equations, consider both the positive and negative roots. For example, the equation \(x^2 = 25\) has two solutions: \(x = 5\) and \(x = -5\).
- Ignoring Absolute Values: The square root of a squared number should be expressed as an absolute value to account for both positive and negative values. For example, \(\sqrt{(-6)^2} = \sqrt{36} = 6\), but since \(\sqrt{(-6)^2} = |-6| = 6\).
By being mindful of these common mistakes, you can improve your accuracy and confidence when working with square roots and squares.
Advanced Mathematical Insights
Exploring the square root of 6 squared involves delving into the realm of real and complex numbers. Understanding this concept can provide deeper insights into mathematical operations and their applications.
When we say the square root of 6 squared, we're essentially asking for the square root of 6 raised to the power of 2. Mathematically, this can be expressed as:
$$\sqrt{(6^2)}$$
To simplify, first, we calculate the square of 6:
$$6^2 = 6 \times 6 = 36$$
Now, taking the square root of 36:
$$\sqrt{36} = 6$$
So, the square root of 6 squared is simply 6. This result highlights a fundamental property of square roots and squares - that they can "cancel out" each other when applied in succession.
Furthermore, this insight extends to understanding the relationship between squares and square roots in the context of real-world applications. Whether in engineering, physics, or finance, knowing how to manipulate and interpret square roots and squares is crucial for solving problems and making informed decisions.
Real-World Examples
Understanding the concept of the square root of 6 squared opens doors to various real-world applications where mathematical principles are applied.
In engineering, for instance, when determining the length of a diagonal in a square, the Pythagorean theorem comes into play. Consider a square with sides of length 6 units. To find the length of the diagonal, we can use the formula:
$$\text{diagonal} = \sqrt{(side^2 + side^2)}$$
Substituting the value of the side (6 units), we get:
$$\text{diagonal} = \sqrt{(6^2 + 6^2)}$$
Calculating:
$$\text{diagonal} = \sqrt{(36 + 36)}$$
$$\text{diagonal} = \sqrt{72}$$
In finance, understanding square roots is essential for calculating risk measures such as standard deviation. For example, in investment analysis, if the expected return on a portfolio is 6% and the standard deviation is 6%, the annualized volatility can be calculated as:
$$\text{Volatility} = \sqrt{(6\%^2)}$$
$$\text{Volatility} = \sqrt{0.36}$$
$$\text{Volatility} ≈ 0.6\%$$
These real-world examples demonstrate the practical significance of grasping mathematical concepts like the square root of 6 squared and its applications across various fields.
Conclusion
In conclusion, exploring the square root of 6 squared has provided us with valuable insights into fundamental mathematical operations and their real-world applications.
Through a comprehensive examination of basic concepts, definitions, and properties related to squares and square roots, we have gained a deeper understanding of mathematical principles.
Furthermore, delving into advanced mathematical insights has allowed us to appreciate the broader significance of these concepts across various disciplines, from engineering to finance.
Real-world examples have illustrated how the square root of 6 squared can be applied in practical scenarios, demonstrating its relevance and utility in problem-solving and decision-making.
Overall, this exploration highlights the beauty and versatility of mathematics, showcasing how seemingly abstract concepts like square roots can have profound implications in our everyday lives.
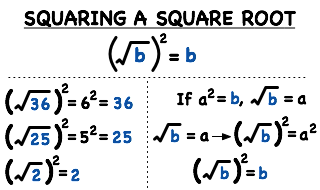
Xem video để hiểu rõ hơn về khái niệm căn bậc hai và cách áp dụng nó trong bài toán căn bậc hai của 6 bình phương.
Giải pháp cho bài toán: Căn bậc hai của 6 bình phương | Toán học với Thầy J
READ MORE:
Xem video để hiểu rõ hơn về khái niệm căn bậc hai và cách giải thích nó một cách dễ hiểu cho trẻ em.
Căn bậc hai là gì? 🚀 Hiểu về Căn bậc hai 👨🏻🚀 Toán học cho Trẻ em