Topic find the square root of 25: Discover the simplicity and significance of finding the square root of 25 in this comprehensive guide. From basic arithmetic principles to practical applications, explore how this fundamental mathematical concept plays a crucial role in various fields. Join us as we delve into the intriguing world of square roots and their relevance in everyday life.
Table of Content
- Square Root of 25
- Understanding the Concept of Square Roots
- Basic Arithmetic: Calculating Square Roots
- Historical Significance of Square Roots
- Practical Applications of Square Roots
- Visual Representation of Square Root of 25
- Mathematical Properties and Formulas
- Conclusion: Square Root of 25 Explained
- YOUTUBE: Video giải thích cách tìm căn bậc hai của 25, phù hợp cho người học muốn hiểu rõ hơn về toán học cơ bản.
Square Root of 25
The square root of 25 is:
$\sqrt{25} = 5$

READ MORE:
Understanding the Concept of Square Roots
The concept of square roots is fundamental in mathematics, representing a number that produces a specified quantity when multiplied by itself. In other words, the square root of a number \( x \) is a value \( y \) such that \( y^2 = x \).
To illustrate, let's delve into the square root of 25:
- Identify the number: 25
- Determine a number that, when squared, equals 25:
- \(5 \times 5 = 25\)
- Thus, the square root of 25 is 5, represented as \( \sqrt{25} = 5 \).
Square roots can be both positive and negative because both \( 5^2 \) and \( (-5)^2 \) equal 25. Therefore, \( \sqrt{25} = \pm 5 \).
Here are some key properties of square roots:
- Non-negative results: The principal square root is always non-negative.
- Perfect squares: Numbers like 25, which have an integer as their square root, are called perfect squares.
- Product property: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Understanding square roots is crucial for advanced mathematical concepts, including solving quadratic equations, analyzing geometric shapes, and understanding various physical phenomena.
Basic Arithmetic: Calculating Square Roots
Calculating the square root of a number is a fundamental arithmetic skill. To find the square root of 25, we follow a straightforward process:
- Identify the number you want to find the square root of: 25.
- Determine if the number is a perfect square by finding an integer that, when multiplied by itself, equals the number:
- Check if 1, 2, 3, 4, and 5 multiplied by themselves equal 25.
- Find the integer that satisfies the condition:
- \(5 \times 5 = 25\).
- Conclude that the square root of 25 is 5:
- \(\sqrt{25} = 5\).
For a more detailed step-by-step approach:
- Prime Factorization Method:
- Write the number as a product of prime factors: \(25 = 5 \times 5\).
- Group the factors into pairs: \((5 \times 5)\).
- Take one factor from each pair: \( \sqrt{25} = 5\).
- Estimation Method:
- Find two perfect squares between which 25 lies: 16 and 36.
- Estimate the square root to be between 4 and 6.
- Refine the estimate to find the exact value: 5.
Here is a table of some perfect squares for reference:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
By understanding and applying these methods, you can easily calculate the square root of any perfect square, enhancing your arithmetic skills and mathematical knowledge.
Historical Significance of Square Roots
The concept of square roots has a rich historical background, dating back to ancient civilizations that recognized its importance in mathematics, architecture, and astronomy. Here, we explore the historical significance of square roots:
- Ancient Egypt:
- The Egyptians used square roots in their architectural designs, ensuring precise measurements for constructing pyramids and temples.
- Babylonian Mathematics:
- Babylonian mathematicians developed methods to approximate square roots, demonstrating advanced arithmetic skills in clay tablets dating back to 1800 BCE.
- Greek Contributions:
- Pythagoras and his followers explored square roots in the context of geometry, particularly in the Pythagorean theorem, which relates the sides of a right triangle.
- Euclid's "Elements" included extensive discussions on the properties of square roots, laying the foundation for future mathematical studies.
- Indian Mathematicians:
- Ancient Indian scholars like Aryabhata and Brahmagupta made significant contributions to the understanding and computation of square roots, using innovative techniques for their time.
- Islamic Golden Age:
- Islamic mathematicians preserved and expanded upon earlier knowledge of square roots, translating Greek texts and contributing original research, which influenced the development of algebra.
- Renaissance and Beyond:
- The Renaissance period saw a revival in mathematical studies, with scholars like Leonardo of Pisa (Fibonacci) introducing the square root symbol (√) we use today.
- The development of calculus by Newton and Leibniz further expanded the applications and understanding of square roots in various scientific fields.
Understanding the historical context of square roots provides valuable insights into how this fundamental concept has shaped mathematical thought and practical applications throughout the ages.
Practical Applications of Square Roots
Square roots have a wide range of practical applications in various fields, from mathematics and engineering to everyday life. Here are some detailed examples of how square roots are used:
- Architecture and Construction:
Architects and engineers often use square roots when designing buildings and structures. For example, they might need to determine the length of a diagonal support beam using the Pythagorean theorem, which involves calculating the square root.
- Physics and Engineering:
Square roots are frequently used in physics equations and engineering calculations. For instance, the formula for calculating the period of a pendulum, \( T = 2\pi\sqrt{\frac{L}{g}} \), involves the square root.
- Finance:
In finance, square roots are used to calculate standard deviations and variances, which are measures of volatility and risk. For example, the standard deviation formula, \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \), includes a square root.
- Medicine:
Square roots are used in various medical calculations, such as determining dosages and understanding statistical results in medical research. For example, the Body Mass Index (BMI) calculation involves a square root when converting between different units.
- Computer Science:
Square roots are essential in algorithms and computer graphics. For instance, the Euclidean distance formula, \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \), is used to calculate the distance between two points in 2D space.
These examples illustrate just a few of the many ways in which square roots play a crucial role in both theoretical and practical applications. Understanding and being able to calculate square roots is an essential skill in many scientific and professional fields.
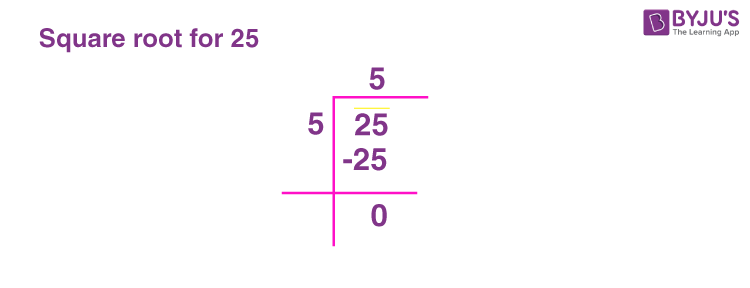
Visual Representation of Square Root of 25
The square root of 25 is a number which, when multiplied by itself, gives the product 25. This value is denoted by the radical symbol as \(\sqrt{25}\).
Visually, this can be represented by considering the geometric properties of squares:
- The area of a square is calculated as the length of one side squared. For instance, if the side length of a square is 5, the area is:
\[ 5 \times 5 = 25 \]
- Conversely, if we know the area of the square is 25, we can determine the side length by taking the square root of the area:
\[ \sqrt{25} = 5 \]
Below is a visual representation:
| 5 | 5 |
| 5 | 5 |
This table shows a 2x2 grid representing the square with each cell having side lengths of 5 units, making the total area 25 square units.
In conclusion, the visual representation of the square root of 25 can be simply seen in the side length of a square that has an area of 25 square units.
Mathematical Properties and Formulas
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 25 is represented as √25.
Here are some key mathematical properties and formulas related to square roots:
- Definition: The square root of 25 is a number that, when squared, equals 25. Mathematically, it can be expressed as:
- \( \sqrt{25} = x \) where \( x^2 = 25 \)
- Therefore, \( x = 5 \) or \( x = -5 \), since \( 5^2 = 25 \) and \( (-5)^2 = 25 \).
- Properties of Square Roots:
- Square roots are non-negative for non-negative inputs: \( \sqrt{25} = 5 \).
- Product property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{25 \cdot 1} = \sqrt{25} \cdot \sqrt{1} = 5 \cdot 1 = 5 \).
- Quotient property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{25}{1}} = \frac{\sqrt{25}}{\sqrt{1}} = \frac{5}{1} = 5 \).
- Formulas Involving Square Roots:
- Pythagorean Theorem: In a right-angled triangle, the length of the hypotenuse \( c \) is given by \( c = \sqrt{a^2 + b^2} \). If \( a = 3 \) and \( b = 4 \), then \( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \).
- Quadratic Formula: The solutions of \( ax^2 + bx + c = 0 \) are given by \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \). For \( x^2 - 25 = 0 \), \( x = \frac{0 \pm \sqrt{0 + 100}}{2 \cdot 1} = \frac{\pm 10}{2} = \pm 5 \).
Understanding these properties and formulas helps in comprehending the concept and applications of square roots in various mathematical problems.
Conclusion: Square Root of 25 Explained
The square root of 25 is a straightforward example of a perfect square, making it a fundamental concept in mathematics. Here are the key points to understand:
- Definition: The square root of a number \( n \) is a number \( r \) such that \( r^2 = n \). For 25, this number is 5 because \( 5^2 = 25 \).
- Mathematical Representation: The square root of 25 can be represented as:
- Radical form: \( \sqrt{25} \)
- Exponential form: \( 25^{1/2} \) or \( 25^{0.5} \)
- Positive and Negative Roots: Both 5 and -5 are square roots of 25 because:
- \( 5^2 = 25 \)
- \( (-5)^2 = 25 \)
- Calculation Methods: There are various methods to find the square root of 25, including:
- Prime Factorization: Breaking down 25 into prime factors gives \( 25 = 5 \times 5 \). Thus, \( \sqrt{25} = 5 \).
- Repeated Subtraction: Subtracting consecutive odd numbers from 25 until zero is reached:
- 25 - 1 = 24
- 24 - 3 = 21
- 21 - 5 = 16
- 16 - 7 = 9
- 9 - 9 = 0
Understanding the square root of 25 not only provides insights into basic arithmetic but also serves as a foundation for more complex mathematical concepts. The simplicity of perfect squares like 25 makes them excellent teaching tools in various mathematical contexts.
Video giải thích cách tìm căn bậc hai của 25, phù hợp cho người học muốn hiểu rõ hơn về toán học cơ bản.
Căn bậc hai của 25
READ MORE:
Video hướng dẫn cách tìm căn bậc hai của 25, giúp người xem nắm vững khái niệm toán học cơ bản và ứng dụng thực tế.
Tìm Căn Bậc Hai: √25