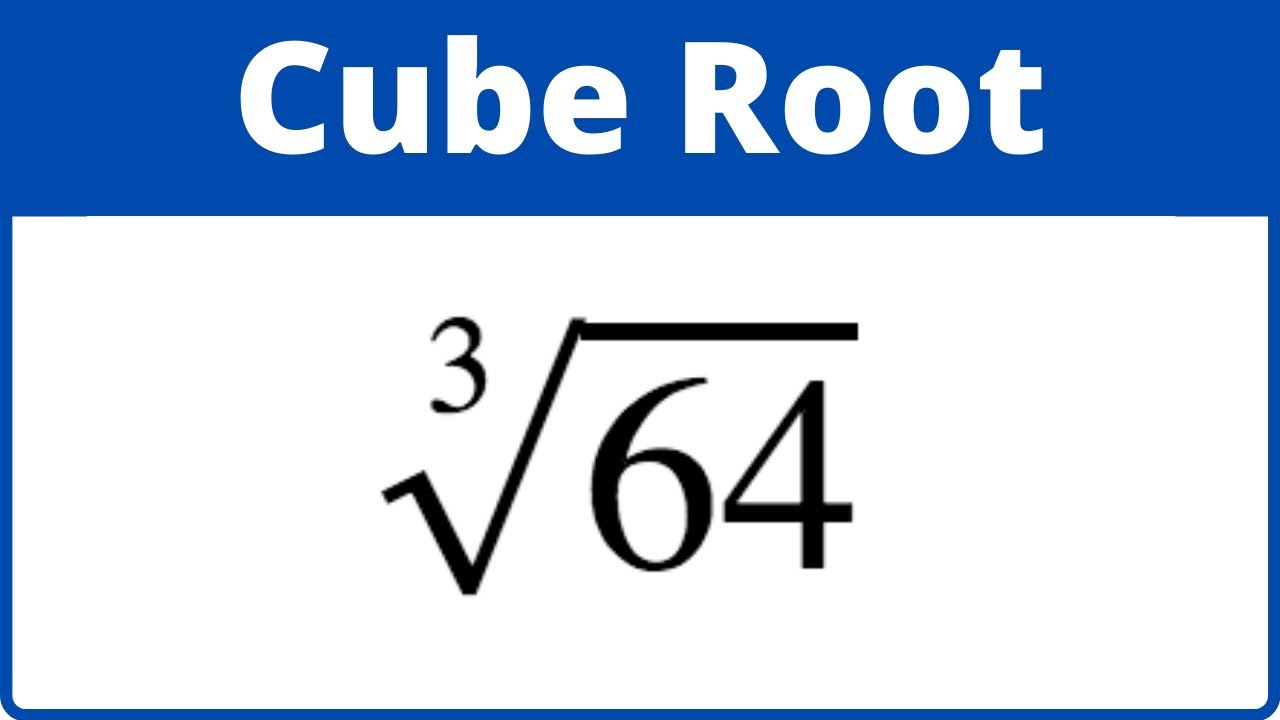
Topic 3 square root 25: Unlock the simplicity of calculating \(3 \sqrt{25}\) in this concise guide. Learn the step-by-step process to simplify this mathematical expression, understand the underlying principles, and see practical applications. Perfect for students and enthusiasts alike, this article will make mastering square roots and their multipliers easy and intuitive.
Table of Content
- Calculating \(3 \sqrt{25}\)
- Introduction to Square Roots
- Basic Principles of Square Roots
- Understanding the Square Root of 25
- Calculating \(3 \sqrt{25}\)
- Step-by-Step Calculation of \(3 \sqrt{25}\)
- Mathematical Properties of Square Roots
- Applications of Square Root Calculations
- Common Mistakes in Calculating Square Roots
- Advanced Square Root Calculations
- Conclusion and Summary
- YOUTUBE:
Calculating \(3 \sqrt{25}\)
To find the value of \(3 \sqrt{25}\), we first need to calculate the square root of 25 and then multiply the result by 3.
Step-by-Step Calculation
- Find the square root of 25:
- \(\sqrt{25} = 5\)
- Multiply the result by 3:
- \(3 \times 5 = 15\)
Result
The value of \(3 \sqrt{25}\) is:
\[ 3 \sqrt{25} = 15 \]

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that help us find a number which, when multiplied by itself, gives the original number. They are widely used in various fields such as geometry, algebra, and physics. Understanding square roots is essential for solving many types of mathematical problems.
Here is a step-by-step explanation to understand square roots better:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). It is denoted as \( \sqrt{x} \).
- Examples:
- \(\sqrt{25} = 5\) because \(5 \times 5 = 25\)
- \(\sqrt{16} = 4\) because \(4 \times 4 = 16\)
- Properties:
- The square root of a positive number is always positive.
- The square root of 0 is 0.
- Negative numbers do not have real square roots (they have imaginary roots).
- Calculating Square Roots:
- For perfect squares (like 25, 16, 9), the square root is an integer.
- For non-perfect squares, the square root can be an irrational number (e.g., \(\sqrt{2}\)).
- Square roots can be calculated using methods such as prime factorization, estimation, and using a calculator.
- Applications:
- Used in solving quadratic equations.
- Applied in geometry to find the lengths of sides in right triangles (Pythagorean theorem).
- Utilized in various scientific calculations involving area and volume.
Understanding square roots is not only crucial for academic purposes but also for practical applications in daily life and various professions.
Basic Principles of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\). The square root is denoted by the radical symbol \( \sqrt{} \).
Here are the basic principles of square roots:
- Non-negative Numbers: Square roots are only defined for non-negative numbers in the set of real numbers. For example, \( \sqrt{25} = 5 \) and \( \sqrt{0} = 0 \).
- Principal Square Root: The principal square root is the non-negative square root of a number. For instance, the principal square root of 25 is 5.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they can be expressed as the square of an integer. For example, 25 is a perfect square because \(25 = 5^2\).
- Properties of Square Roots:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) for any non-negative numbers \(a\) and \(b\).
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for any non-negative numbers \(a\) and \(b\) where \(b \neq 0\).
- \( (\sqrt{a})^2 = a \) for any non-negative number \(a\).
- Irrational Numbers: The square roots of non-perfect squares are irrational numbers. For example, \( \sqrt{2} \) is an irrational number because it cannot be expressed as a simple fraction.
Understanding these basic principles is essential for mastering square root calculations and their applications in various mathematical problems.
Understanding the Square Root of 25
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is a number that, when squared, equals 25.
To understand the square root of 25, consider the following steps:
- Identify the number for which you want to find the square root. In this case, the number is 25.
- Recognize that the square root of a number \( x \) is denoted as \( \sqrt{x} \).
- Use the definition of a square root: \( \sqrt{25} = x \) where \( x^2 = 25 \).
- Determine the value of \( x \) that satisfies this equation. We need to find \( x \) such that \( x \times x = 25 \).
- From basic multiplication, we know that \( 5 \times 5 = 25 \). Therefore, \( \sqrt{25} = 5 \).
- Consider both the positive and negative roots: While 5 is a common solution, remember that \( (-5) \times (-5) = 25 \) as well. However, by convention, the principal square root is the positive value. Thus, \( \sqrt{25} = 5 \).
To summarize, the square root of 25 is 5 because 5 multiplied by itself equals 25.
| Expression | Value |
|---|---|
| \( \sqrt{25} \) | 5 |
| \( 5^2 \) | 25 |
Calculating \(3 \sqrt{25}\)
To calculate \(3 \sqrt{25}\), follow these steps:
- Recognize that \(\sqrt{25} = 5\) because 5 multiplied by itself equals 25.
- Multiply 3 by the value obtained in step 1: \(3 \times 5 = 15\).
Therefore, \(3 \sqrt{25} = 15\).
Step-by-Step Calculation of \(3 \sqrt{25}\)
To calculate \(3 \sqrt{25}\), follow these detailed steps:
- Identify the square root of 25. Since \(\sqrt{25} = 5\) (because \(5 \times 5 = 25\)), this is the first step.
- Next, multiply the number outside the square root (which is 3) by the result from step 1. \(3 \times 5 = 15\).
Therefore, \(3 \sqrt{25} = 15\).
Mathematical Properties of Square Roots
Square roots have several important properties:
- Definition: The square root of a number \( x \), denoted as \( \sqrt{x} \), is a value that, when multiplied by itself, gives \( x \).
- Basic Properties:
- \(\sqrt{a} \times \sqrt{b} = \sqrt{ab}\) for non-negative numbers \( a \) and \( b \).
- \(\sqrt{a^2} = |a|\), where \( |a| \) represents the absolute value of \( a \).
- Product Rule: \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \).
- Quotient Rule: \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \) for \( b \neq 0 \).
- Square Root of 25: Specifically, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
Applications of Square Root Calculations
Square root calculations are widely used in various practical applications:
- Geometry: Calculating dimensions and areas of squares, rectangles, and circles.
- Physics: Determining velocities, accelerations, and forces in mechanics.
- Engineering: Estimating strengths of materials and analyzing structural integrity.
- Finance: Evaluating risks and returns in investment portfolios.
- Statistics: Calculating standard deviations and measures of dispersion.
- Computer Graphics: Adjusting brightness, contrast, and colors in digital images.
Common Mistakes in Calculating Square Roots
When calculating square roots, avoid these common errors:
- Incorrect Value: Using the wrong number under the square root sign.
- Missing Negative Sign: Forgetting to include the negative sign when appropriate.
- Order of Operations: Misplacing operations, such as addition or multiplication, within the calculation.
- Not Simplifying: Failing to simplify square roots when possible.
- Confusion with Variables: Mixing up variables and constants in algebraic expressions involving square roots.

Advanced Square Root Calculations
In this section, we will delve into more complex scenarios involving square roots, exploring advanced techniques and properties. These include operations with nested radicals, solving equations involving square roots, and understanding the behavior of square roots in different mathematical contexts.
Operations with Nested Radicals
Nested radicals involve taking the square root of a number that is itself under a square root. For example:
\[
\sqrt{2 + \sqrt{3}}
\]
To simplify such expressions, we often use the method of squaring both sides and solving for the nested term:
- Assume \(\sqrt{2 + \sqrt{3}} = x\).
- Square both sides: \((\sqrt{2 + \sqrt{3}})^2 = x^2\).
- This simplifies to \(2 + \sqrt{3} = x^2\).
- Isolate the square root term: \(\sqrt{3} = x^2 - 2\).
- Square both sides again: \(3 = (x^2 - 2)^2\).
- Expand and solve the resulting quadratic equation.
Solving Equations Involving Square Roots
Consider the equation:
\[
\sqrt{x + 5} = x - 1
\]
To solve this, follow these steps:
- Square both sides to eliminate the square root: \((\sqrt{x + 5})^2 = (x - 1)^2\).
- This gives: \(x + 5 = x^2 - 2x + 1\).
- Rearrange into a standard quadratic equation: \(x^2 - 3x - 4 = 0\).
- Factorize or use the quadratic formula to find the values of \(x\).
- Check each solution in the original equation to verify validity.
Behavior of Square Roots in Different Contexts
Understanding how square roots behave in various mathematical contexts is crucial for advanced calculations. Here are some key points:
- Square Roots and Exponents: \(\sqrt{x} = x^{1/2}\), allowing the use of exponent rules for manipulation.
- Square Roots of Negative Numbers: These involve imaginary numbers, where \(\sqrt{-1} = i\), and extend into complex number theory.
- Square Roots in Calculus: Square roots appear frequently in calculus, particularly in limits, derivatives, and integrals involving functions with square root terms.
Example Problem: Simplifying a Complex Expression
Let's simplify the following expression:
\[
\sqrt{50} + 3\sqrt{2}
\]
Step-by-step simplification:
- Factor the term inside the square root: \(\sqrt{50} = \sqrt{25 \times 2}\).
- Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\): \(\sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2}\).
- Since \(\sqrt{25} = 5\): \(5\sqrt{2}\).
- Combine like terms: \(5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2}\).
Applications in Higher Mathematics
Square roots are used extensively in higher mathematics and applied fields:
- Engineering: In signal processing, control systems, and electrical engineering, square roots are part of key equations and models.
- Physics: Quantum mechanics, relativity, and other areas of physics often involve square root calculations.
- Statistics: Standard deviation, a measure of dispersion in data sets, is calculated using square roots.
By mastering these advanced square root calculations, you can handle a wide range of mathematical problems with greater confidence and precision.
Conclusion and Summary
Throughout this guide, we have explored various aspects of square roots, culminating in the calculation of \(3 \sqrt{25}\). Let's summarize the key points:
- Understanding Square Roots: We started with the basics, defining what a square root is and how it functions in mathematics.
- Principles and Properties: We discussed fundamental principles and properties of square roots, including how to simplify and manipulate them.
- Specific Calculation: The focus was on calculating \(3 \sqrt{25}\), which simplifies to \(3 \times 5 = 15\).
- Step-by-Step Process: We provided a detailed, step-by-step guide to reach the final result, ensuring clarity in the calculation process.
- Applications: We explored practical applications of square roots in various fields such as geometry and algebra.
- Common Mistakes: We highlighted common errors to avoid when working with square roots.
- Advanced Calculations: We delved into more complex scenarios involving square roots, including methods for simplifying radicals and combining different root expressions.
In conclusion, mastering the calculation of square roots, such as \(3 \sqrt{25}\), not only enhances your mathematical skills but also prepares you for more advanced mathematical concepts. By understanding the theory, practicing calculations, and applying these skills in various contexts, you can gain a deeper appreciation and competence in mathematics.
We hope this guide has been comprehensive and helpful in your journey to understanding and calculating square roots. Remember, practice is key to proficiency in mathematics, so continue to explore and solve different square root problems to strengthen your skills.
Căn bậc hai của 25
READ MORE:
Cách Đơn Giản Hóa Căn Bậc Hai của 25: sqrt(25)