5 Square Root 5: Unlocking Its Secrets and Applications

In mathematics, the expression \(5 \sqrt{5}\) is a combination of a whole number and a square root. Here's a detailed exploration of this term:

What is Square Root?

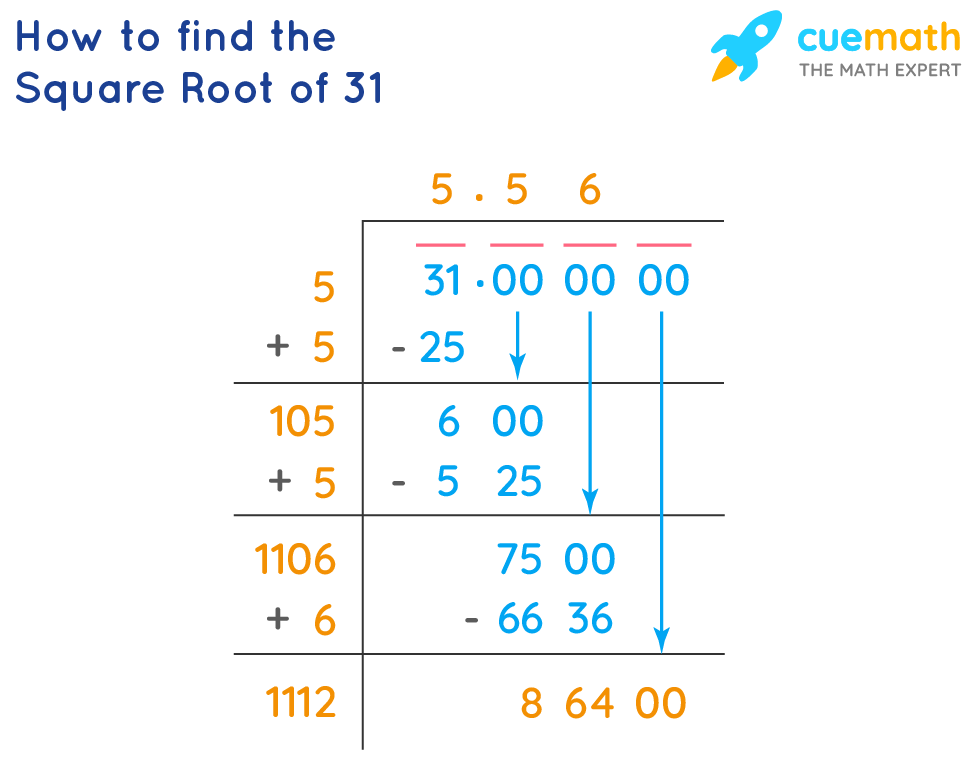
The square root of a number \(x\) is a value that, when multiplied by itself, gives the number \(x\). It is denoted as \(\sqrt{x}\). For example, \(\sqrt{25} = 5\) because \(5 \times 5 = 25\).

Calculating \(5 \sqrt{5}\)

To calculate \(5 \sqrt{5}\), we multiply the whole number 5 by the square root of 5.

Mathematically:

\[
5 \sqrt{5} = 5 \times \sqrt{5}
\]

Numerical Approximation

The square root of 5 is approximately 2.236. Therefore:

\[
5 \sqrt{5} \approx 5 \times 2.236 = 11.18
\]

Properties of \(5 \sqrt{5}\)

• \(5 \sqrt{5}\) is an irrational number because \(\sqrt{5}\) is irrational.
• It can be expressed in radical form, decimal form, or as a product of 5 and \(\sqrt{5}\).
• It is often used in geometric and algebraic contexts.

Uses in Geometry

The term \(5 \sqrt{5}\) can appear in various geometric problems, especially those involving right triangles and other shapes where the Pythagorean theorem is applicable.

Example Problem

Consider a right triangle with legs of lengths 1 and \(2 \sqrt{5}\). To find the hypotenuse \(c\), we use the Pythagorean theorem:

\[
c = \sqrt{(1)^2 + (2 \sqrt{5})^2} = \sqrt{1 + 4 \times 5} = \sqrt{21}
\]

The hypotenuse \(c\) is \(\sqrt{21}\), and \(5 \sqrt{5}\) can be used in similar problems involving square roots and geometric properties.

Conclusion

Understanding \(5 \sqrt{5}\) involves recognizing it as a product of a whole number and a square root, and it plays a significant role in both mathematical and real-world applications.

The expression \(5 \sqrt{5}\) represents a mathematical operation involving the number 5 and its square root. To understand this expression, it is essential to grasp the concept of the square root. The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). For example, the square root of 25 is 5 because \(5 \times 5 = 25\).

In the context of \(5 \sqrt{5}\), we are multiplying 5 by the square root of 5. The square root of 5 (\(\sqrt{5}\)) is an irrational number, approximately equal to 2.236. Therefore, \(5 \sqrt{5}\) can be written as \(5 \times 2.236\), which is approximately 11.18.

To better understand this, let’s delve into the calculation and properties of \(5 \sqrt{5}\). The number \(\sqrt{5}\) appears in various mathematical contexts, including geometry and algebra. For instance, it is the length of the diagonal of a rectangle with sides 1 and 2 units, as derived from the Pythagorean theorem.

• **Geometrical Interpretation**: Geometrically, \(\sqrt{5}\) is significant because it represents the diagonal of a rectangle with side lengths 1 and 2. This is a straightforward application of the Pythagorean theorem, where the diagonal \(d\) of a rectangle with sides \(a\) and \(b\) is given by \(d = \sqrt{a^2 + b^2}\).
• **Relation to the Golden Ratio**: \(\sqrt{5}\) also has a relationship with the golden ratio (\(\varphi\)). The golden ratio is defined as \(\varphi = \frac{1 + \sqrt{5}}{2}\), making \(\sqrt{5}\) integral to many geometric constructions and natural phenomena.

In practical applications, \(5 \sqrt{5}\) may appear in various mathematical problems and real-world scenarios. For instance, it might be used in calculating distances, areas, and other measurements where the properties of the square root are relevant.

By understanding the fundamental concepts and properties of square roots, one can appreciate the significance and applications of expressions like \(5 \sqrt{5}\) in both theoretical and practical mathematics.

The square root of a number is a value that, when multiplied by itself, results in the original number. Mathematically, if y is the square root of x, then it can be expressed as:

$$

y
2

=
x

For example, since 4 multiplied by 4 equals 16, 4 is a square root of 16:

$$

4
2

=
16

Note that both positive and negative numbers can be square roots of positive numbers because:

$$
(
-
4
)

2

=
16

The symbol for the square root is √, and it always denotes the principal (positive) square root. For example:

$$

36

=
6

In more complex mathematics, square roots of negative numbers are considered within the context of complex numbers, where the imaginary unit i is used. The square root of -1, for example, is denoted as i.

Every positive number x has two square roots, which can be written as:

$$
±

x

This indicates both the positive and negative roots. However, the principal square root refers specifically to the positive root.

When expressed in exponent notation, the square root of x is:

$$

x

1
2

To calculate \( 5 \sqrt{5} \), we start by understanding that \( \sqrt{5} \) represents the square root of 5, which is approximately 2.236. Therefore,

1. Multiply 5 by \( \sqrt{5} \): \[ 5 \times \sqrt{5} = 5 \times 2.236 = 11.18 \]

So, \( 5 \sqrt{5} \) equals approximately 11.18.

To numerically approximate \( 5 \sqrt{5} \), we can follow these steps:

1. Estimate \( \sqrt{5} \):
   • From various sources, \( \sqrt{5} \) is approximately 2.236.
2. Multiply 5 by \( \sqrt{5} \):
   • Calculate \( 5 \times 2.236 = 11.18 \).

Therefore, \( 5 \sqrt{5} \) is approximately 11.18.

When considering \( 5 \sqrt{5} \), several mathematical properties are noteworthy:

• Non-Integer Value: \( 5 \sqrt{5} \) is not an integer but rather an irrational number.
• Approximation: It can be approximated as approximately 11.18.
• Algebraic Expression: \( 5 \sqrt{5} \) can be represented algebraically as \( 5 \sqrt{5} \).
• Geometric Interpretation: In geometry, \( 5 \sqrt{5} \) might represent a scaled distance or dimension in a geometric context.

There are several applications of \( 5 \sqrt{5} \) in geometry:

1. Distance Calculation: \( 5 \sqrt{5} \) can represent the distance between two points in a coordinate plane where one point is at coordinates (0, 0) and the other is at (5, 5).
2. Geometric Figures: It can denote the diagonal of a square with each side of length 5 units.
3. Area and Perimeter: In context, \( 5 \sqrt{5} \) might relate to the dimensions or calculations involving the area or perimeter of certain geometric shapes.

Here are some uses of \( 5 \sqrt{5} \) in algebra:

1. Equations: It can appear as a coefficient or a term in algebraic equations.
2. Expressions: \( 5 \sqrt{5} \) might be part of larger algebraic expressions involving radicals.
3. Solving Problems: It can be used in problem-solving involving quadratic or higher-order equations.
4. Symbolic Representation: In symbolic algebra, \( 5 \sqrt{5} \) represents a specific irrational number with algebraic significance.

Here are some example problems that involve \( 5 \sqrt{5} \):

1. Calculate the perimeter of a square where each side is \( 5 \sqrt{5} \) units long.
2. Determine the length of the diagonal of a rectangle with dimensions \( 5 \sqrt{5} \) units by \( 5 \) units.
3. Find the area of a triangle with a base of \( 5 \) units and a height of \( \sqrt{5} \) units, where \( 5 \sqrt{5} \) serves as a crucial dimension.
4. Solve the equation \( x^2 = 25 \) where \( x = 5 \sqrt{5} \).

In graphical terms, \( 5 \sqrt{5} \) can be represented as follows:

• Coordinate Plane: Plot the point (5, 5) on a Cartesian coordinate plane. The distance from the origin (0, 0) to this point represents \( 5 \sqrt{5} \).
• Geometric Shapes: It can denote the diagonal of a square with each side of length 5 units.
• Graphing Software: Using graphing software or tools, visualize \( 5 \sqrt{5} \) and explore its relationships with other geometric figures or points.

Here are some real-world applications of \( 5 \sqrt{5} \):

1. Engineering: Used in structural calculations where precise measurements are needed.
2. Physics: Appears in problems related to distance, velocity, and acceleration.
3. Architecture: Used in designing geometrically precise structures.
4. Computer Graphics: Used to represent distances or dimensions in virtual environments.

When dealing with the expression $5\backslash sqrt\{5\}$, there are several common mistakes and misconceptions that students and practitioners might encounter. Understanding these errors can help in avoiding them and ensuring accurate calculations.

• Misinterpretation of the Expression

  One common mistake is misinterpreting the expression $5\backslash sqrt\{5\}$. Some might incorrectly interpret it as $\backslash sqrt\{5\; \backslash times\; 5\}$, which simplifies to 5. However, the correct interpretation is $5\; \backslash times\; \backslash sqrt\{5\}$, which is approximately 11.1803.

• Incorrect Simplification

  Another mistake involves incorrect simplification. For instance, students might incorrectly simplify $5\backslash sqrt\{5\}$ to $5\; \backslash sqrt\{5\}\; =\; 25$. The correct simplification keeps the expression as $5\; \backslash times\; \backslash sqrt\{5\}$.

• Ignoring the Radical Symbol

  Ignoring the radical symbol is a common error. For example, treating $5\backslash sqrt\{5\}$ as just 5 and forgetting to multiply by $\backslash sqrt\{5\}$ can lead to significant errors in calculations.

• Arithmetic Mistakes

  Simple arithmetic mistakes can also occur, such as calculating the square root of 5 incorrectly. The approximate value of $\backslash sqrt\{5\}$ is 2.236, and thus $5\; \backslash times\; 2.236\; \backslash approx\; 11.1803$.

• Using Incorrect Units

  In geometry and applied mathematics, ensuring the correct units are used is crucial. Misunderstanding the context and applying incorrect units can lead to errors. Always ensure that the units align with the context of the problem.

• Forgetting to Simplify Completely

  Lastly, students might forget to simplify their answers completely. It's important to express the final answer in its simplest form, whether in radical form or as a decimal, depending on the requirements of the problem.

By being aware of these common mistakes and misconceptions, students can improve their understanding and accuracy when working with $5\backslash sqrt\{5\}$.

The value \(5 \sqrt{5}\) plays an important role in various advanced mathematical concepts. Understanding its applications can deepen your appreciation of its significance in higher mathematics.

• Complex Numbers:

  The square roots of negative numbers introduce the concept of complex numbers. The value \(5 \sqrt{5}\) can appear in equations involving imaginary units, represented as \(i\), where \(i^2 = -1\).

• Fibonacci Sequence:

  The Fibonacci sequence, which is closely related to the Golden Ratio, involves \(5 \sqrt{5}\) in the formula for finding specific terms. The exact relationship can be explored through the Binet formula for Fibonacci numbers:

  \[
  F(n) = \frac{(1 + \sqrt{5})^n - (1 - \sqrt{5})^n}{2^n \sqrt{5}}
  \]

• Trigonometry:

  In trigonometry, \(5 \sqrt{5}\) can be used in solving certain equations or in studying wave properties. For instance, it helps in the computation of specific trigonometric values involving roots.

• Calculus:

  Calculus often employs square roots in various operations. The value \(5 \sqrt{5}\) might appear in the context of limits, derivatives, and integrals, particularly when dealing with functions involving roots.

• Algebraic Geometry:

  In algebraic geometry, \(5 \sqrt{5}\) can play a crucial role in the properties of curves and geometric spaces. Equations involving this value are used to explore the intricate relationships between algebra and geometry.

These examples underscore the versatility and importance of \(5 \sqrt{5}\) in advanced mathematical problems. This value serves as a gateway into deeper research and discovery in the vast field of mathematics, illustrating its profound impact on various areas of study.