Topic the square root of 25: The square root of 25 is a fundamental concept in mathematics, offering a gateway to understanding more complex mathematical principles. This article explores the calculation, properties, and real-world applications of the square root of 25, providing a comprehensive guide for learners and enthusiasts alike. Discover the significance of this simple yet essential mathematical operation.
Table of Content
- The Square Root of 25
- Introduction
- Understanding Square Roots
- What is the Square Root of 25?
- Calculating the Square Root of 25
- Positive and Negative Roots
- Perfect Squares and Their Roots
- Applications of Square Roots
- Mathematics and Quadratic Equations
- Physics and Engineering Uses
- Graphing the Square Root Function
- Common Misconceptions
- Practice Problems
- Conclusion
- YOUTUBE:
The Square Root of 25
The square root of 25 is a mathematical calculation that determines which number, when multiplied by itself, equals 25. The symbol for the square root is √. Therefore, we can represent this as √25.
Calculation
The number 25 can be expressed as:
$$25 = 5 \times 5$$
Therefore, the square root of 25 is:
$$\sqrt{25} = 5$$
Detailed Explanation
When you take the square root of a number, you are looking for a value that, when squared (multiplied by itself), gives the original number. In the case of 25:
- 5 is the number that, when multiplied by itself (5 × 5), equals 25.
Properties of Square Roots
- Positive and Negative Roots: While the principal square root of 25 is 5, there is also a negative root, which is -5, because (-5) × (-5) = 25.
- Perfect Square: 25 is a perfect square because its square root is an integer.
Applications
The concept of square roots is widely used in various fields such as:
- Mathematics: Solving quadratic equations, simplifying expressions, and more.
- Physics: Calculating distances, forces, and in various formulas.
- Engineering: Structural analysis, electronics, and other calculations.
Square Root Function
The square root function can be represented graphically. For the function \( f(x) = \sqrt{x} \), the graph is a curve that starts at the origin (0,0) and increases gradually. For \( x = 25 \), \( f(25) = 5 \).
Here's a simple table of values for the square root function:
| x | f(x) = √x |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Understanding the square root of 25 and its properties helps build a strong foundation in mathematics and its applications in real-world problems.

READ MORE:
Introduction
The square root of 25 is a key mathematical concept that opens doors to understanding various mathematical operations and theories. It involves finding a number which, when multiplied by itself, equals 25. This operation is fundamental in algebra, geometry, and beyond. Understanding the square root of 25 can help simplify complex equations and enhance problem-solving skills.
In mathematical notation, the square root is represented by the radical symbol √. The equation for the square root of 25 is expressed as:
$$\sqrt{25} = 5$$
This is because:
$$5 \times 5 = 25$$
The square root of 25 can be understood through the following steps:
- Identify the number you want the square root of, in this case, 25.
- Determine which number, when multiplied by itself, results in 25.
- Recognize that 5 multiplied by 5 equals 25, so the square root of 25 is 5.
Moreover, the concept of square roots extends beyond just whole numbers. It plays a crucial role in various mathematical fields and real-world applications, such as solving quadratic equations, analyzing geometric shapes, and in physics and engineering calculations.
The exploration of square roots, including the square root of 25, forms a vital part of mathematical education and helps build a strong foundation for advanced studies.
Understanding Square Roots
The concept of a square root is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, if x is the square root of y, then \( x^2 = y \).
Square roots can be both positive and negative. For any positive number y, there are two square roots: a positive square root (denoted as \( \sqrt{y} \)) and a negative square root (denoted as \( -\sqrt{y} \)). These roots are symmetrically located on the number line.
Notation
In mathematical notation, the square root of a number y is represented as \( \sqrt{y} \). For example, the square root of 25 is represented as \( \sqrt{25} \).
Properties of Square Roots
- Non-negativity: The principal square root (the positive square root) of a non-negative number is non-negative.
- Product Property: The square root of a product is the product of the square roots. For example, \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Quotient Property: The square root of a quotient is the quotient of the square roots. For example, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for \( b \neq 0 \).
- Even and Odd Powers: The square root of a number raised to an even power is the number raised to half that power. For example, \( \sqrt{x^4} = x^2 \).
Examples
- \( \sqrt{4} = 2 \) because \( 2 \times 2 = 4 \).
- \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \).
- \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
- \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
Visual Representation
To visualize the concept of square roots, consider the area of a square. The side length of the square is the square root of its area. For example, a square with an area of 25 square units has sides of length 5 units because \( 5 \times 5 = 25 \).
Understanding square roots is essential for solving quadratic equations, working with exponents, and performing various calculations in algebra and geometry.
What is the Square Root of 25?
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 25, the square root is the value which satisfies the equation:
\[ \sqrt{25} = x \]
In other words, we are looking for a number \( x \) such that:
\[ x^2 = 25 \]
There are two numbers that satisfy this equation:
\[ 5 \times 5 = 25 \quad \text{and} \quad (-5) \times (-5) = 25 \]
Thus, the square roots of 25 are \( +5 \) and \( -5 \). However, when we refer to "the square root" without specifying the sign, we typically mean the principal (positive) square root. Therefore:
\[ \sqrt{25} = 5 \]
Let's explore some properties of the square root of 25:
- 25 is a perfect square because its square root is a whole number.
- The square root of 25 can be simplified to an integer, 5.
- The square root of 25 is rational since it can be expressed as a fraction (5/1).
Here are different ways to represent the square root of 25:
- Using the radical sign: \( \sqrt{25} \)
- Using exponents: \( 25^{1/2} \)
The square root of 25 is used in various mathematical contexts. For example, in geometry, it can be used to find the length of a side of a square when the area is known. Since the area of a square is the side length squared, knowing that the area is 25 square units means each side is 5 units long.
Understanding that the square root of 25 is 5 helps in solving quadratic equations, simplifying expressions, and analyzing mathematical problems involving squares and square roots.
Calculating the Square Root of 25
Calculating the square root of 25 can be approached in various ways, including prime factorization, using a calculator, and manual methods like long division. Here, we will explore these methods step by step.
Using Prime Factorization
Prime factorization is a method where we break down the number into its prime factors. For 25, this process looks like this:
- 25 can be expressed as \( 5 \times 5 \).
- Taking the square root of both sides, we get: \[ \sqrt{25} = \sqrt{5 \times 5} = 5 \]
Using a Calculator
If you have a calculator, calculating the square root of 25 is straightforward:
- Enter 25 into the calculator.
- Press the square root (√) button.
- The result will be 5.
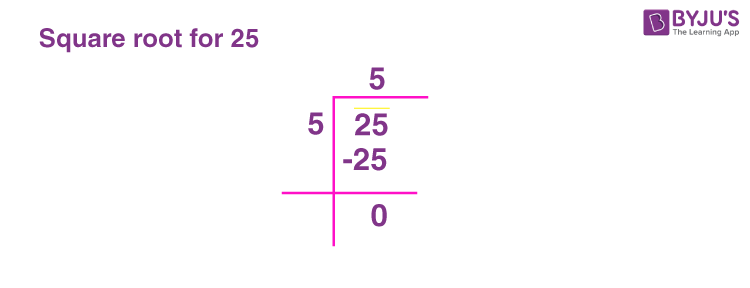
Using Long Division Method
The long division method is another manual way to find the square root of a number:
- Pair the digits of the number from right to left. Since 25 has only two digits, it forms one pair: (25).
- Find the largest number whose square is less than or equal to 25. This number is 5 because \( 5^2 = 25 \).
- Place the 5 on top as the quotient and subtract \( 25 \) from 25 to get 0, indicating the division is exact.
- Thus, the square root of 25 is 5.
Using Exponents
The square root of a number can also be expressed using exponents. The square root of 25 can be written as:
\[
\sqrt{25} = 25^{\frac{1}{2}}
\]
This notation is often used in higher mathematics and helps in understanding the relationship between roots and exponents.
In summary, the square root of 25 is 5, and it can be calculated using several methods, all of which demonstrate the consistency and simplicity of finding square roots for perfect squares.

Positive and Negative Roots
When considering the square root of a number, it is essential to understand that there are both positive and negative roots. For any positive number \( n \), the equation \( \sqrt{n} \) has two solutions: a positive root and a negative root.
For example, in the case of 25:
- The positive square root is denoted by \( \sqrt{25} \), which equals 5.
- The negative square root is denoted by \( -\sqrt{25} \), which equals -5.
This is because both \( 5 \times 5 = 25 \) and \( (-5) \times (-5) = 25 \). Thus, the number 25 has two square roots:
- \( \sqrt{25} = 5 \) (positive square root)
- \( -\sqrt{25} = -5 \) (negative square root)
In general, for any positive number \( a \), the principal (positive) square root is \( \sqrt{a} \), and the negative square root is \( -\sqrt{a} \). This can be summarized as follows:
| Number | Positive Square Root | Negative Square Root |
|---|---|---|
| 25 | \( \sqrt{25} = 5 \) | \( -\sqrt{25} = -5 \) |
| 36 | \( \sqrt{36} = 6 \) | \( -\sqrt{36} = -6 \) |
| 49 | \( \sqrt{49} = 7 \) | \( -\sqrt{49} = -7 \) |
It is important to note that the square root of zero is unique:
- \( \sqrt{0} = 0 \)
Understanding both the positive and negative roots is crucial in solving various mathematical problems, especially in algebra and geometry.
Perfect Squares and Their Roots
Perfect squares are the squares of whole numbers. When you multiply a whole number by itself, the product is called a perfect square. The process of finding the square root is essentially the reverse of finding a perfect square. Here are some examples:
- 1 is a perfect square because \(1^2 = 1\).
- 4 is a perfect square because \(2^2 = 4\).
- 9 is a perfect square because \(3^2 = 9\).
- 16 is a perfect square because \(4^2 = 16\).
- 25 is a perfect square because \(5^2 = 25\).
- 36 is a perfect square because \(6^2 = 36\).
- 49 is a perfect square because \(7^2 = 49\).
- 64 is a perfect square because \(8^2 = 64\).
- 81 is a perfect square because \(9^2 = 81\).
- 100 is a perfect square because \(10^2 = 100\).
The square root of a perfect square is always an integer. For example, the square root of 25 is 5 because \(5^2 = 25\).
Here is a table of perfect squares and their roots:
| Number | Perfect Square | Square Root |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 2 |
| 3 | 9 | 3 |
| 4 | 16 | 4 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 7 |
| 8 | 64 | 8 |
| 9 | 81 | 9 |
| 10 | 100 | 10 |
Memorizing the perfect squares up to 12 can be very useful in various mathematical calculations and problem-solving scenarios.
Applications of Square Roots
Square roots are fundamental in various practical applications across different fields. Here are some notable examples:
- Geometry and Construction:
Square roots are essential in geometry, especially when dealing with areas and lengths of sides of squares and other shapes. For instance, if the area of a square is given, the length of its side can be found by taking the square root of the area. In construction, calculating diagonal lengths and other dimensions often involves square roots.
- Pythagorean Theorem:
Square roots play a crucial role in the Pythagorean theorem, which is used to find the length of a side in a right triangle. The theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides, which often requires taking square roots to solve.
For example, if the legs of a right triangle are 3 and 4 units, the hypotenuse is found by:
\[ c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Quadratic Equations:
The quadratic formula, used to solve quadratic equations, includes a square root. The solutions of the equation \( ax^2 + bx + c = 0 \) are given by:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Here, the term under the square root, \( b^2 - 4ac \), is called the discriminant and determines the nature of the roots.
- Physics and Engineering:
Square roots are used in various physics equations, such as those involving gravitational acceleration. For instance, the time \( t \) it takes for an object to fall from a height \( h \) is calculated by:
\[ t = \frac{\sqrt{2h}}{g} \]
where \( g \) is the acceleration due to gravity.
- Distance Calculations:
In both two-dimensional and three-dimensional space, the distance between two points is calculated using the distance formula, which involves square roots. For two points \((x_1, y_1)\) and \((x_2, y_2)\), the distance \( D \) is:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
For three-dimensional space, the formula extends to:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
- Financial Mathematics:
Square roots are used in financial calculations, such as determining the standard deviation in statistics, which measures the amount of variation or dispersion of a set of values. The standard deviation \( \sigma \) is calculated as:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \]
where \( N \) is the number of observations, \( x_i \) are the individual values, and \( \mu \) is the mean of the values.
Mathematics and Quadratic Equations
Square roots play a vital role in solving quadratic equations. A quadratic equation is any equation that can be rearranged in standard form as:
\( ax^2 + bx + c = 0 \)
Here, \(a\), \(b\), and \(c\) are constants, and \(a \neq 0\). There are several methods to solve quadratic equations, including:
- Factoring: This method involves expressing the quadratic equation as a product of its factors. If the quadratic can be factored, it can be written as:
- Completing the Square: This method transforms the quadratic equation into a perfect square trinomial. By adding and subtracting a suitable constant, the equation takes the form:
- Quadratic Formula: The quadratic formula provides a direct way to find the roots of any quadratic equation. The formula is:
- If \(b^2 - 4ac > 0\), the equation has two distinct real roots.
- If \(b^2 - 4ac = 0\), the equation has exactly one real root.
- If \(b^2 - 4ac < 0\), the equation has two complex roots.
- Graphing: Quadratic equations can also be solved by graphing the quadratic function \(y = ax^2 + bx + c\) and identifying the points where the graph intersects the x-axis. These intersection points represent the roots of the equation.
\( (x - r_1)(x - r_2) = 0 \)
where \(r_1\) and \(r_2\) are the roots of the quadratic equation.
\( (x + d)^2 = e \)
Taking the square root of both sides results in two possible solutions:
\( x + d = \pm \sqrt{e} \)
Solving for \(x\) gives:
\( x = -d \pm \sqrt{e} \)
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
Here, \( \sqrt{b^2 - 4ac} \) is the discriminant, which determines the nature of the roots:
The use of square roots in these methods highlights their significance in understanding and solving quadratic equations. Whether through factoring, completing the square, or using the quadratic formula, mastering these techniques is essential for tackling a wide range of problems in algebra.

Physics and Engineering Uses
The square root function plays a crucial role in various applications in physics and engineering. Understanding its uses helps in solving complex problems and designing efficient systems.
- Calculating Magnitudes: In physics, the square root is used to determine the magnitude of vectors. For instance, the magnitude of a vector \( \vec{v} \) with components \( v_x \) and \( v_y \) is given by \( \sqrt{v_x^2 + v_y^2} \). This is essential in mechanics to find the resultant force or velocity.
- Wave Mechanics: The square root function appears in the Schrödinger equation in quantum mechanics, where it helps describe the wave function of particles.
- Electrical Engineering: In AC circuits, the root mean square (RMS) value of an alternating current is calculated using the square root. The RMS value is crucial for determining the power consumption of electrical devices.
- Structural Engineering: The square root is used in calculating the natural frequencies of structures. For example, the natural frequency \( f \) of a simple harmonic oscillator is given by \( f = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \), where \( k \) is the stiffness and \( m \) is the mass.
- Fluid Dynamics: In fluid flow analysis, the square root function helps determine flow rates and velocities. The Bernoulli equation, which describes the behavior of fluid under varying conditions of flow and height, often involves square root calculations.
- Thermodynamics: The square root is used in the ideal gas law to relate the velocity of gas molecules to temperature: \( v = \sqrt{\frac{3kT}{m}} \), where \( k \) is the Boltzmann constant, \( T \) is the temperature, and \( m \) is the mass of a gas molecule.
- Aerospace Engineering: Calculating escape velocity involves the square root. The escape velocity \( v_e \) from a planet is given by \( v_e = \sqrt{\frac{2GM}{R}} \), where \( G \) is the gravitational constant, \( M \) is the mass of the planet, and \( R \) is its radius.
These applications highlight the importance of the square root function in various scientific and engineering fields, providing a foundation for solving practical problems and advancing technology.
Graphing the Square Root Function
The graph of the square root function is a distinctive curve that begins at a certain point and increases slowly as it moves to the right. Here is a detailed step-by-step process to graph the square root function \( y = \sqrt{x} \):
-
Identify the Domain: The domain of the square root function is all non-negative values of \( x \), since the square root of a negative number is not a real number. Therefore, the domain is \( x \geq 0 \).
-
Create a Table of Values: Select a range of \( x \)-values within the domain and compute the corresponding \( y \)-values.
\( x \) \( y = \sqrt{x} \) 0 0 1 1 4 2 9 3 16 4 -
Plot the Points: Using the table of values, plot the points on a graph. Start with the point (0,0) and continue with the points (1,1), (4,2), (9,3), and so on.
-
Draw the Curve: Connect the points with a smooth curve. The graph should start at (0,0) and curve upward to the right, becoming less steep as \( x \) increases.
-
Consider Transformations: If the function has been modified, such as \( y = a\sqrt{x-h} + k \), apply transformations accordingly:
- Vertical Stretch/Compression: Multiplying by a factor \( a \) stretches (if \( |a| > 1 \)) or compresses (if \( 0 < |a| < 1 \)) the graph vertically.
- Horizontal Shift: Adding/subtracting \( h \) shifts the graph left/right.
- Vertical Shift: Adding/subtracting \( k \) shifts the graph up/down.
Graphing the square root function correctly involves careful plotting of points and a smooth connection of these points, resulting in a curve that accurately represents the function's behavior.
Common Misconceptions
Understanding square roots can sometimes be tricky, and there are several common misconceptions that can lead to confusion. Below, we clarify some of these misunderstandings to help build a stronger foundation in mathematics.
- Only Positive Roots: One prevalent misconception is that square roots are always positive. While it is true that the principal square root (the most commonly referred to square root) is positive, every positive number actually has two square roots: one positive and one negative. For example, the square roots of 25 are both 5 and -5.
- Negative Numbers Can't Have Square Roots: Another misconception is that negative numbers cannot have square roots. While negative numbers do not have real number square roots, they do have imaginary roots. The square root of a negative number introduces the concept of imaginary numbers, such as \( \sqrt{-25} = 5i \), where \( i \) is the imaginary unit defined as \( \sqrt{-1} \).
- Squaring a Negative Root: Some believe that squaring a negative square root results in a negative number. In reality, squaring any number, whether positive or negative, results in a positive number. For instance, \( (-5)^2 = 25 \).
- Calculating Negative Square Roots is More Complex: There is a notion that calculating negative square roots is more complex than their positive counterparts. The process is essentially the same, involving an understanding of the properties of square roots and imaginary numbers.
- \(\sqrt{x^2} = \pm x\): A common teaching in schools is that \( \sqrt{x^2} = \pm x \). However, this is not entirely accurate when considering the principal square root, which is always non-negative. The correct interpretation is that \( \sqrt{x^2} = |x| \), meaning the absolute value of \( x \). When solving equations such as \( x^2 = 25 \), it is correct to write \( x = \pm 5 \) because both positive and negative solutions are valid, but the square root function itself is defined to return only the non-negative root.
Clarifying these misconceptions helps in developing a better understanding of mathematical concepts and their applications. By addressing these common errors, learners can enhance their problem-solving skills and mathematical literacy.
Practice Problems
Below are some practice problems designed to help you understand and calculate square roots. Try solving them step by step.
-
Calculate the square root of 25.
Solution:
- \(\sqrt{25} = 5\)
-
Find the square root of 36 using prime factorization.
Solution:
- Prime factors of 36: \(2 \times 2 \times 3 \times 3\)
- Group the factors in pairs: \((2 \times 2) \times (3 \times 3)\)
- Take one factor from each pair: \(2 \times 3 = 6\)
- Therefore, \(\sqrt{36} = 6\)
-
Simplify \(\sqrt{64}\).
Solution:
- \(\sqrt{64} = 8\)
-
Find the square root of 144 by prime factorization.
Solution:
- Prime factors of 144: \(2 \times 2 \times 2 \times 2 \times 3 \times 3\)
- Group the factors in pairs: \((2 \times 2) \times (2 \times 2) \times (3 \times 3)\)
- Take one factor from each pair: \(2 \times 2 \times 3 = 12\)
- Therefore, \(\sqrt{144} = 12\)
-
Evaluate \(\sqrt{100}\).
Solution:
- \(\sqrt{100} = 10\)
-
Find the square root of 81 using the prime factorization method.
Solution:
- Prime factors of 81: \(3 \times 3 \times 3 \times 3\)
- Group the factors in pairs: \((3 \times 3) \times (3 \times 3)\)
- Take one factor from each pair: \(3 \times 3 = 9\)
- Therefore, \(\sqrt{81} = 9\)
-
Calculate the square root of 169.
Solution:
- \(\sqrt{169} = 13\)
-
Find the square root of 225 by prime factorization.
Solution:
- Prime factors of 225: \(3 \times 3 \times 5 \times 5\)
- Group the factors in pairs: \((3 \times 3) \times (5 \times 5)\)
- Take one factor from each pair: \(3 \times 5 = 15\)
- Therefore, \(\sqrt{225} = 15\)
-
Simplify \(\sqrt{49}\).
Solution:
- \(\sqrt{49} = 7\)
-
Find the square root of 1024 by prime factorization.
Solution:
- Prime factors of 1024: \(2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\)
- Group the factors in pairs: \((2 \times 2) \times (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times (2 \times 2)\)
- Take one factor from each pair: \(2 \times 2 \times 2 \times 2 \times 2 = 32\)
- Therefore, \(\sqrt{1024} = 32\)
Conclusion
The exploration of the square root of 25 reveals the simplicity and fundamental nature of this mathematical concept. As we have seen, the square root of 25 is 5, a straightforward result derived through various methods, including prime factorization, repeated subtraction, and the long division method. This value is a perfect square and a rational number, illustrating the consistency and reliability of mathematical principles.
Understanding square roots not only enhances our grasp of basic arithmetic but also provides a foundation for more complex mathematical topics such as quadratic equations and geometric calculations. The concept of square roots is widely applicable, from solving real-world problems in physics and engineering to enhancing our comprehension of abstract mathematical theories.
Overall, the journey through the properties, calculations, and applications of the square root of 25 underscores the importance of mastering fundamental math skills. By demystifying common misconceptions and engaging in practice problems, we build a solid mathematical foundation that is crucial for academic success and practical problem-solving.
Căn bậc hai của 25
READ MORE:
Căn bậc hai của 25 là gì? Hầu hết không hiểu tại sao họ có câu trả lời ĐÚNG!