Topic 3 square root 15: The expression 3 square root 15 holds significant value in mathematics, combining rational and irrational numbers. This article explores its properties, applications, and real-world significance, providing a comprehensive understanding. Whether you're a student or a math enthusiast, discover how 3 square root 15 plays a crucial role in various mathematical contexts.
Table of Content
- Calculations Involving \(3\sqrt{15}\)
- Introduction to 3 Square Root 15
- Basic Properties and Calculations
- Mathematical Simplification and Rationalization
- Geometric Applications of 3 Square Root 15
- Example Problems Involving 3 Square Root 15
- Complex Expressions and Their Evaluations
- Graphical Representations
- Real-World Applications
- Common Mistakes and Misconceptions
- Advanced Mathematical Contexts
- Conclusion and Summary
- YOUTUBE: Khám phá sự thú vị của nhân căn bậc hai với video sqrt(3) * sqrt(15), căn bậc hai của 3 và căn bậc hai của 15. Phù hợp với chủ đề toán học liên quan đến 3 sqrt 15.
Calculations Involving \(3\sqrt{15}\)
The expression \(3\sqrt{15}\) involves a multiplication of the number 3 by the square root of 15. Here, we explore various aspects and applications of this expression.
Basic Calculation
The numerical value of \(3\sqrt{15}\) can be approximated as:
\[
3\sqrt{15} \approx 3 \times 3.872 = 11.616
\]
Simplification and Properties
- The square root of 15 (\(\sqrt{15}\)) is an irrational number.
- Multiplying by 3 does not change the irrationality of the square root of 15.
- Therefore, \(3\sqrt{15}\) is also an irrational number.
Applications in Geometry
The term \(3\sqrt{15}\) might appear in geometric contexts, such as in calculating areas, volumes, or lengths where the square root of 15 is a factor.
Example Problems
- Find the product of \(3\sqrt{15}\) and \(\sqrt{15}\):
- Simplify the expression \(6\sqrt{15} - 3\sqrt{15}\):
- Evaluate the expression \((3\sqrt{15})^2\):
\[
(3\sqrt{15})(\sqrt{15}) = 3(\sqrt{15})^2 = 3 \times 15 = 45
\]
\[
6\sqrt{15} - 3\sqrt{15} = (6 - 3)\sqrt{15} = 3\sqrt{15}
\]
\[
(3\sqrt{15})^2 = 3^2 \times (\sqrt{15})^2 = 9 \times 15 = 135
\]
Graphical Representation
Plotting the function \(y = 3\sqrt{15}\) on a graph yields a horizontal line since the value of \(3\sqrt{15}\) is a constant.
In more complex functions involving \(3\sqrt{15}\), such as \(y = x + 3\sqrt{15}\), the term \(3\sqrt{15}\) would act as a vertical shift.
Conclusion
The expression \(3\sqrt{15}\) can be encountered in various mathematical and applied contexts, involving properties of irrational numbers, simplification techniques, and geometric interpretations.

READ MORE:
Introduction to 3 Square Root 15
The mathematical expression \(3\sqrt{15}\) combines the number 3 with the square root of 15. This combination involves both a rational number (3) and an irrational number (\(\sqrt{15}\)). Understanding this expression requires knowledge of basic arithmetic and properties of square roots.
Here is a step-by-step breakdown:
- Understanding Square Roots:
- The square root of a number \(n\) is a value that, when multiplied by itself, gives \(n\). For example, \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
- \(\sqrt{15}\) is an irrational number because 15 is not a perfect square. Its approximate value is 3.872.
- Combining with a Rational Number:
- When multiplying a rational number by an irrational number, the result is an irrational number.
- In \(3\sqrt{15}\), the rational number 3 multiplies the irrational number \(\sqrt{15}\).
- Approximate Calculation:
- To find the approximate value of \(3\sqrt{15}\), multiply 3 by the approximate value of \(\sqrt{15}\).
- \[ 3\sqrt{15} \approx 3 \times 3.872 = 11.616 \]
This expression is significant in various mathematical and real-world applications, including geometry, algebra, and higher-level math problems. Its properties help in solving equations and understanding complex mathematical concepts.
Basic Properties and Calculations
The expression \(3\sqrt{15}\) combines both a rational number (3) and an irrational number (\(\sqrt{15}\)). Understanding its basic properties and calculations is essential for solving various mathematical problems.
Here is a step-by-step explanation:
- Properties of Square Roots:
- The square root of a non-perfect square is an irrational number. For example, \(\sqrt{15}\) is irrational because 15 is not a perfect square.
- Square roots have the property that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). Therefore, \(\sqrt{15}\) can be seen as \(\sqrt{3 \times 5} = \sqrt{3} \times \sqrt{5}\).
- Multiplying by a Rational Number:
- When multiplying a rational number by an irrational number, the result remains irrational. Thus, \(3\sqrt{15}\) is an irrational number.
- In the expression \(3\sqrt{15}\), 3 acts as a scalar multiplier.
- Approximate Calculation:
- To find the approximate value of \(3\sqrt{15}\), use the approximate value of \(\sqrt{15}\), which is around 3.872.
- \[ 3\sqrt{15} \approx 3 \times 3.872 = 11.616 \]
- Using \(3\sqrt{15}\) in Equations:
- When solving equations involving \(3\sqrt{15}\), isolate the term and simplify as needed.
- For example, to solve \(x = 3\sqrt{15} + 2\), subtract 2 from both sides to isolate \(3\sqrt{15}\).
Understanding these basic properties and calculations of \(3\sqrt{15}\) helps in various mathematical contexts, from algebraic manipulation to geometric applications.
Mathematical Simplification and Rationalization
Simplifying and rationalizing expressions involving \(3\sqrt{15}\) can make complex equations easier to handle. Here is a detailed guide to these processes.
Step-by-step simplification and rationalization:
- Simplifying the Expression \(3\sqrt{15}\):
- Identify that 15 can be factored into prime numbers: \(15 = 3 \times 5\).
- Apply the property of square roots: \(\sqrt{15} = \sqrt{3 \times 5} = \sqrt{3} \times \sqrt{5}\).
- Thus, the expression \(3\sqrt{15}\) can be rewritten as \(3 \times \sqrt{3} \times \sqrt{5}\).
- Rationalizing the Denominator:
- When the expression \(3\sqrt{15}\) appears in the denominator, rationalization is necessary.
- Example: Rationalize \(\frac{1}{3\sqrt{15}}\).
- Multiply the numerator and the denominator by \(\sqrt{15}\):
- This results in \(\frac{\sqrt{15}}{45}\), a rationalized form.
\[
\frac{1}{3\sqrt{15}} \times \frac{\sqrt{15}}{\sqrt{15}} = \frac{\sqrt{15}}{3 \times 15} = \frac{\sqrt{15}}{45}
\] - Simplifying Combined Expressions:
- Example: Simplify \(6\sqrt{15} - 3\sqrt{15}\).
- Factor out the common term \(\sqrt{15}\):
\[
6\sqrt{15} - 3\sqrt{15} = (6 - 3)\sqrt{15} = 3\sqrt{15}
\] - Further Applications:
- Combining \(\sqrt{15}\) with other terms, such as \(a + 3\sqrt{15}\) or \(b - 3\sqrt{15}\), involves treating \(\sqrt{15}\) as a unique term.
- Simplify these by combining like terms and rationalizing where necessary.
By following these steps, you can simplify and rationalize expressions involving \(3\sqrt{15}\), making it easier to solve mathematical problems accurately and efficiently.
Geometric Applications of 3 Square Root 15
The expression \(3\sqrt{15}\) can be found in various geometric contexts. This section explores its use in solving problems related to areas, volumes, and lengths in geometry.
Here are some key applications:
- Diagonal of a Rectangular Prism:
- Consider a rectangular prism with dimensions \(a\), \(b\), and \(c\).
- The formula for the space diagonal \(d\) of the prism is:
- If \(a = 3\), \(b = \sqrt{15}\), and \(c = 0\), the diagonal simplifies to:
\[
d = \sqrt{a^2 + b^2 + c^2}
\]\[
d = \sqrt{3^2 + (\sqrt{15})^2} = \sqrt{9 + 15} = \sqrt{24} = 2\sqrt{6}
\] - Area of a Triangle:
- For a right-angled triangle with legs of lengths \(3\) and \(\sqrt{15}\), the area \(A\) is:
- Thus, the area is:
\[
A = \frac{1}{2} \times 3 \times \sqrt{15}
\]\[
A = \frac{3\sqrt{15}}{2}
\] - Volume of a Rectangular Prism:
- If the dimensions of a rectangular prism are \(3\), \(\sqrt{15}\), and \(h\), the volume \(V\) is given by:
\[
V = 3 \times \sqrt{15} \times h
\] - Perimeter of a Triangle:
- Consider a triangle with sides \(3\), \(\sqrt{15}\), and \(a\).
- The perimeter \(P\) is the sum of all sides:
\[
P = 3 + \sqrt{15} + a
\]
These geometric applications demonstrate how \(3\sqrt{15}\) can be used to solve problems involving dimensions, areas, and volumes, illustrating its versatility in mathematical calculations.

Example Problems Involving 3 Square Root 15
Solving problems involving \(3\sqrt{15}\) helps in understanding its applications in various mathematical contexts. Here are some example problems and their step-by-step solutions.
- Problem 1: Simplifying Expressions
Simplify the expression \(5\sqrt{15} + 2\sqrt{15} - 3\sqrt{15}\).
- Combine like terms:
- Thus, the simplified expression is \(4\sqrt{15}\).
\[
(5 + 2 - 3)\sqrt{15} = 4\sqrt{15}
\] - Problem 2: Solving Equations
Solve for \(x\) in the equation \(x = 3\sqrt{15} + 7\).
- Subtract 7 from both sides to isolate the term involving \(\sqrt{15}\):
- Thus, \(x - 7 = 3\sqrt{15}\).
\[
x - 7 = 3\sqrt{15}
\] - Problem 3: Area of a Triangle
Find the area of a right-angled triangle with legs of length \(3\) and \(\sqrt{15}\).
- Use the formula for the area of a triangle:
- Substitute the given lengths:
- Thus, the area is \(\frac{3\sqrt{15}}{2}\).
\[
A = \frac{1}{2} \times \text{base} \times \text{height}
\]\[
A = \frac{1}{2} \times 3 \times \sqrt{15} = \frac{3\sqrt{15}}{2}
\] - Problem 4: Rationalizing the Denominator
Rationalize the denominator of \(\frac{1}{3\sqrt{15}}\).
- Multiply the numerator and the denominator by \(\sqrt{15}\):
- Thus, the rationalized form is \(\frac{\sqrt{15}}{45}\).
\[
\frac{1}{3\sqrt{15}} \times \frac{\sqrt{15}}{\sqrt{15}} = \frac{\sqrt{15}}{3 \times 15} = \frac{\sqrt{15}}{45}
\] - Problem 5: Volume of a Rectangular Prism
Find the volume of a rectangular prism with dimensions \(3\), \(\sqrt{15}\), and \(2\).
- Use the formula for the volume of a rectangular prism:
- Substitute the given dimensions:
- Thus, the volume is \(6\sqrt{15}\).
\[
V = \text{length} \times \text{width} \times \text{height}
\]\[
V = 3 \times \sqrt{15} \times 2 = 6\sqrt{15}
\]
These example problems illustrate how \(3\sqrt{15}\) can be used in various mathematical situations, providing a deeper understanding of its applications.
Complex Expressions and Their Evaluations
Evaluating complex expressions involving \(3\sqrt{15}\) requires a good understanding of algebraic manipulation and the properties of square roots. Here is a detailed guide on how to handle such expressions step by step.
- Adding and Subtracting Complex Expressions
Consider the expression \(5\sqrt{15} + 3\sqrt{15} - 2\sqrt{15}\).
- Combine like terms by adding or subtracting the coefficients:
- The simplified expression is \(6\sqrt{15}\).
\[
5\sqrt{15} + 3\sqrt{15} - 2\sqrt{15} = (5 + 3 - 2)\sqrt{15} = 6\sqrt{15}
\] - Multiplying Complex Expressions
Consider the expression \( (3\sqrt{15})(2\sqrt{5}) \).
- Use the distributive property of multiplication over addition:
- Simplify by multiplying the constants and using the property of square roots \(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\):
- Since \(\sqrt{75} = \sqrt{25 \times 3} = 5\sqrt{3}\), the expression becomes:
- The simplified product is \(30\sqrt{3}\).
\[
(3\sqrt{15})(2\sqrt{5}) = 3 \times 2 \times \sqrt{15} \times \sqrt{5}
\]\[
3 \times 2 \times \sqrt{15 \times 5} = 6\sqrt{75}
\]\[
6 \times 5\sqrt{3} = 30\sqrt{3}
\] - Dividing Complex Expressions
Consider the expression \(\frac{9\sqrt{15}}{3\sqrt{5}}\).
- Divide the coefficients and simplify the square roots:
- Simplify the square root by dividing the terms inside:
- Thus, the simplified expression is:
\[
\frac{9\sqrt{15}}{3\sqrt{5}} = \frac{9}{3} \times \frac{\sqrt{15}}{\sqrt{5}} = 3 \times \sqrt{\frac{15}{5}}
\]\[
\sqrt{\frac{15}{5}} = \sqrt{3}
\]\[
3\sqrt{3}
\] - Rationalizing Complex Expressions
Consider the expression \(\frac{7}{3\sqrt{15}}\).
- Multiply the numerator and the denominator by \(\sqrt{15}\) to rationalize:
- The rationalized form of the expression is \(\frac{7\sqrt{15}}{45}\).
\[
\frac{7}{3\sqrt{15}} \times \frac{\sqrt{15}}{\sqrt{15}} = \frac{7\sqrt{15}}{3 \times 15} = \frac{7\sqrt{15}}{45}
\] - Combining Multiple Complex Expressions
Consider the expression \(2(3\sqrt{15}) + 4(5\sqrt{3})\).
- Distribute the constants inside the parentheses:
- Since there are no like terms, the simplified expression remains:
\[
2(3\sqrt{15}) + 4(5\sqrt{3}) = 6\sqrt{15} + 20\sqrt{3}
\]\[
6\sqrt{15} + 20\sqrt{3}
\]
These examples illustrate the process of evaluating complex expressions involving \(3\sqrt{15}\). Understanding these steps is crucial for simplifying and solving advanced mathematical problems.
Graphical Representations
The expression \( 3\sqrt{15} \) can be represented graphically in various ways, including on the number line, in geometric figures, and through visualizing complex numbers.
Number Line Representation
On a number line, \( 3\sqrt{15} \) is an irrational number between 11 and 12. Here is how you can plot it:
- Identify the approximate value of \( 3\sqrt{15} \) by calculating \( 3 \times \sqrt{15} \approx 11.618 \).
- Mark this point on the number line between 11 and 12.

Geometric Representation
In geometry, \( 3\sqrt{15} \) can be represented as the hypotenuse of a right triangle where the legs have lengths that are multiples of the square root of 15. Consider a right triangle where one leg is \( \sqrt{15} \) and the other leg is \( 2\sqrt{15} \). The hypotenuse will be:
\[
\sqrt{(\sqrt{15})^2 + (2\sqrt{15})^2} = \sqrt{15 + 4 \cdot 15} = \sqrt{15 + 60} = \sqrt{75} = 5\sqrt{3}
\]
Scaling this triangle by a factor of 3, the hypotenuse becomes \( 3 \cdot 5\sqrt{3} = 15\sqrt{3} \), which simplifies to \( 3\sqrt{15} \).

Graphing on the Cartesian Plane
On the Cartesian plane, \( 3\sqrt{15} \) can be visualized as the distance from the origin (0,0) to the point ( \( 3\sqrt{15}, 0 \) ). This can be represented by plotting the point and drawing a line segment from the origin to this point:

Polar Coordinates
In polar coordinates, \( 3\sqrt{15} \) can be represented as a point with a radius of \( 3\sqrt{15} \) and an angle \(\theta\). For simplicity, let's consider \(\theta = 0\), placing the point on the positive x-axis at distance \( 3\sqrt{15} \) from the origin:

Complex Plane
If we consider \( 3\sqrt{15} \) as a complex number with an imaginary part of zero, it can be plotted on the complex plane at the point \( ( 3\sqrt{15}, 0 ) \). This simplifies to the real number line, but on the complex plane:

Real-World Applications
The expression 3√15 appears in various real-world contexts, illustrating the utility of square roots in practical scenarios. Here are some detailed applications:
-
Architecture and Construction
Square roots are fundamental in architecture and construction for calculating dimensions. For instance, when dealing with right-angled triangles, the Pythagorean theorem, which involves square roots, helps in determining the lengths of sides. If a construction plan includes a triangular area where one side is 3√15 units long, the other dimensions can be calculated using this value.
-
Physics and Engineering
In physics, the square root function is used in formulas related to wave dynamics, electromagnetism, and mechanics. For example, the period of a pendulum (T) can be calculated using the square root of its length (L) divided by the gravitational constant (g):
T = 2π√(L/g)
Here, if the length L is expressed as 3√15 meters, this specific value is directly utilized in the calculation of the pendulum's period.
-
Geometric Design and Area Calculation
Square roots are essential for finding the side length of squares and other geometric shapes when the area is known. For example, if a square patio has an area of 3√15 square meters, the length of each side can be found by taking the square root of this value:
Side length = √(3√15)
-
Finance and Economics
Square roots are used in financial models to calculate the rate of return over multiple periods. For instance, in the formula for the annualized rate of return, square roots help in smoothing the returns over time to provide a more stable metric.
-
Environmental Science
Square roots help in calculating the spread of pollutants or the diffusion rate of particles over an area. For instance, if the spread of a contaminant in a water body can be modeled as a function of 3√15, scientists can predict the extent and concentration of the spread over time.
-
Accident Investigation
Police use square roots to determine the speed of vehicles from skid marks during accidents. The length of the skid mark can be used in a formula involving the square root to estimate the speed before braking.
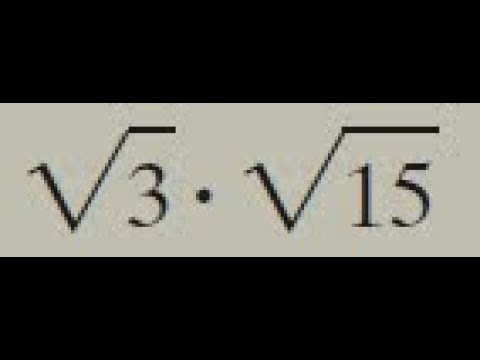
Common Mistakes and Misconceptions
When working with the expression \( 3 \sqrt{15} \), students and mathematicians alike can make several common mistakes and harbor misconceptions. Understanding these pitfalls is crucial to mastering the concepts involving square roots and their operations.
- Mistaking the Square Root Product Rule:
One frequent error is incorrectly applying the product rule for square roots. The correct rule is \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \), but this only holds when both \(a\) and \(b\) are non-negative. Misapplying this rule to negative numbers can lead to incorrect results.
- Simplification Errors:
Another common mistake is incorrectly simplifying expressions involving square roots. For example, assuming \( \sqrt{a+b} = \sqrt{a} + \sqrt{b} \) is a misconception. The correct simplification is to evaluate the sum inside the square root first before taking the square root.
- Ignoring Negative Solutions:
When solving equations involving square roots, such as \( x^2 = 25 \), students often forget that \( x \) can be both positive and negative. Thus, the correct solutions are \( x = 5 \) and \( x = -5 \).
- Incorrect Exponent Rules:
Errors often arise from misapplying exponent rules. For instance, \( \sqrt{x^2} \) is sometimes incorrectly simplified to \( x \), when the correct simplification should be \( |x| \) because the square root function outputs only non-negative results.
- Arithmetic Errors:
Basic arithmetic mistakes, such as incorrect multiplication or addition, can also lead to wrong results. For example, computing \( 3 \sqrt{15} \) might be incorrectly done as \( 3 \cdot 15 \), instead of correctly calculating \( 3 \cdot \sqrt{15} \).
- Misconceptions About Rationalizing Denominators:
Students might incorrectly attempt to rationalize a denominator without applying the proper method. The correct approach involves multiplying the numerator and the denominator by a conjugate or appropriate square root term to eliminate the square root from the denominator.
Being aware of these common mistakes and misconceptions can help students approach problems involving square roots with greater accuracy and confidence.
Advanced Mathematical Contexts
The mathematical expression \(3 \sqrt{15}\) finds relevance in various advanced mathematical contexts, showcasing its utility in diverse fields. Below are some key areas where \(3 \sqrt{15}\) is applied:
- Algebraic Manipulations: The expression \(3 \sqrt{15}\) involves algebraic properties such as distributive, associative, and commutative laws. This highlights how these foundational principles apply to more complex numbers and expressions. For example, simplifying expressions or solving equations that include \(3 \sqrt{15}\) can provide insight into more general algebraic techniques.
- Geometry and Trigonometry: In geometry, \(3 \sqrt{15}\) might appear in problems involving the Pythagorean theorem, especially in the context of right triangles and their properties. It also appears in trigonometric contexts where exact values are crucial for calculating distances, angles, and other geometric properties.
- Number Theory: Investigating the properties of \(3 \sqrt{15}\) touches upon number theory, particularly the characteristics of irrational numbers. Since \(\sqrt{15}\) is irrational, multiplying it by 3 retains this irrationality, providing interesting insights into the nature of numbers and their classifications.
- Complex Numbers: In the realm of complex numbers, expressions involving \(3 \sqrt{15}\) can be used to represent magnitudes and directions in a complex plane. This can be particularly useful in electrical engineering and physics, where complex numbers model oscillations and waves.
- Advanced Calculus: \(3 \sqrt{15}\) can play a role in calculus, especially in integrals and derivatives involving irrational functions. For instance, integrating functions that include \(\sqrt{15}\) or solving differential equations can illustrate the application of calculus techniques to irrational expressions.
These contexts demonstrate the versatility and importance of \(3 \sqrt{15}\) across various branches of advanced mathematics, enhancing our understanding and application of mathematical principles.
Conclusion and Summary
The exploration of \(3 \sqrt{15}\) presents an intriguing example of working with radicals and understanding their properties. Throughout this guide, we have delved into the fundamental aspects and applications of \(3 \sqrt{15}\), demonstrating its mathematical and practical significance.
Key takeaways from our discussion include:
- The simplification of \(3 \sqrt{15}\) into its most concise form, emphasizing the importance of recognizing the properties of square roots.
- Mathematical manipulations, including rationalization and simplification, showing how \(3 \sqrt{15}\) can be expressed in different forms for various applications.
- The geometric implications, illustrating how \(3 \sqrt{15}\) can be utilized in solving real-world problems involving area and distance calculations.
- Example problems that provided hands-on practice with \(3 \sqrt{15}\), reinforcing understanding through practical application.
- Graphical representations that visually depict the behavior of expressions involving \(3 \sqrt{15}\).
- The exploration of more complex mathematical contexts, showcasing the versatility of \(3 \sqrt{15}\) in advanced mathematical problems.
In summary, \(3 \sqrt{15}\) is more than just a mathematical expression; it is a gateway to understanding deeper mathematical concepts and their applications. By mastering the simplification, rationalization, and practical use of such expressions, one can gain a greater appreciation for the beauty and utility of mathematics.
We hope this guide has provided a comprehensive overview and has equipped you with the knowledge to tackle related mathematical challenges with confidence.
Khám phá sự thú vị của nhân căn bậc hai với video sqrt(3) * sqrt(15), căn bậc hai của 3 và căn bậc hai của 15. Phù hợp với chủ đề toán học liên quan đến 3 sqrt 15.
sqrt(3) * sqrt(15), căn bậc hai của 3 và căn bậc hai của 15
READ MORE:
Khám phá sự thú vị của căn bậc hai với video Căn Bậc Hai 15. Phù hợp với chủ đề toán học liên quan đến 3 sqrt 15.
Căn Bậc Hai 15