Topic square root of 25 rational or irrational: The square root of 25 is a fundamental concept in mathematics, often questioned whether it's rational or irrational. This article explores definitions, properties, and examples to clarify this intriguing topic. Read on to understand the nature of the square root of 25 and its relevance in both theoretical and practical applications.
Table of Content
- Is the Square Root of 25 Rational or Irrational?
- Introduction to Rational and Irrational Numbers
- Definition of Rational Numbers
- Definition of Irrational Numbers
- Understanding Square Roots
- The Square Root of 25
- Calculating the Square Root of 25
- Properties of the Square Root of 25
- Is the Square Root of 25 Rational?
- Is the Square Root of 25 Irrational?
- Proof of Rationality
- Examples of Rational Numbers
- Examples of Irrational Numbers
- Importance of Understanding Rational and Irrational Numbers
- Applications of Square Roots in Real Life
- Conclusion
- YOUTUBE: Video này chứng minh rằng căn bậc hai của bất kỳ số nguyên nào cũng là vô tỷ, ngoại trừ các số chính phương. Khám phá lý thuyết toán học và các chứng minh cụ thể.
Is the Square Root of 25 Rational or Irrational?
The square root of 25 is a rational number.
A rational number is defined as any number that can be expressed in the form \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \).
For the square root of 25:
Here, 5 can be expressed as \( \frac{5}{1} \), which fits the definition of a rational number.
Therefore, the square root of 25 is rational.

READ MORE:
Introduction to Rational and Irrational Numbers
Understanding the distinction between rational and irrational numbers is fundamental in mathematics. Here's a detailed look at both types:
Rational Numbers
- Rational numbers are numbers that can be expressed as a fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer.
- Examples include: \( \frac{1}{2} \), \( -3 \), and \( 4.75 \) (which can be written as \( \frac{19}{4} \)).
- In decimal form, rational numbers either terminate or repeat.
Irrational Numbers
- Irrational numbers cannot be expressed as a simple fraction.
- Examples include: \( \pi \), \( \sqrt{2} \), and \( e \).
- In decimal form, irrational numbers are non-terminating and non-repeating.
Comparing Rational and Irrational Numbers
| Rational Numbers | Irrational Numbers |
|---|---|
| Can be expressed as \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \). | Cannot be expressed as \( \frac{p}{q} \). |
| Decimal form terminates or repeats. | Decimal form neither terminates nor repeats. |
| Examples: \( \frac{3}{4}, 5, 0.333\ldots \) (repeating decimal). | Examples: \( \sqrt{3}, \pi, e \). |
This distinction between rational and irrational numbers is crucial as it forms the foundation for understanding more complex mathematical concepts, including the nature of square roots.
Definition of Rational Numbers
Rational numbers are a key concept in mathematics, essential for understanding various mathematical operations and real-world applications. Here is a detailed explanation:
Rational Numbers are defined as numbers that can be expressed in the form of a fraction \( \frac{p}{q} \), where \( p \) and \( q \) are integers, and \( q \neq 0 \).
Characteristics of Rational Numbers
- They can be positive, negative, or zero.
- The fraction \( \frac{p}{q} \) is in its simplest form if the greatest common divisor (GCD) of \( p \) and \( q \) is 1.
- In decimal form, rational numbers either terminate or repeat.
Examples of Rational Numbers
| Number | Fraction Form | Decimal Form |
|---|---|---|
| \( \frac{1}{2} \) | \( \frac{1}{2} \) | 0.5 |
| \( -3 \) | \( \frac{-3}{1} \) | -3.0 |
| \( 4.75 \) | \( \frac{19}{4} \) | 4.75 |
| \( 0.333\ldots \) | \( \frac{1}{3} \) | 0.333... (repeating decimal) |
Steps to Determine if a Number is Rational
- Check if the number can be expressed as a fraction \( \frac{p}{q} \) where both \( p \) and \( q \) are integers and \( q \neq 0 \).
- Simplify the fraction by dividing both the numerator and the denominator by their GCD.
- Convert the number to its decimal form to see if it terminates or repeats. If it does, the number is rational.
Understanding rational numbers is crucial as they form the basis for many mathematical concepts and operations, making them indispensable in both academic and practical contexts.
Definition of Irrational Numbers
Irrational numbers are a fundamental concept in mathematics, representing numbers that cannot be expressed as simple fractions. Here is a detailed explanation:
Irrational Numbers are defined as numbers that cannot be written in the form of a fraction \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \).
Characteristics of Irrational Numbers
- They cannot be expressed as a ratio of two integers.
- Their decimal expansions are non-terminating and non-repeating.
- They often arise from the square roots of non-perfect squares and certain mathematical constants.
Examples of Irrational Numbers
| Number | Description | Decimal Form |
|---|---|---|
| \( \pi \) | Ratio of the circumference to the diameter of a circle. | 3.14159... |
| \( e \) | Base of the natural logarithm. | 2.71828... |
| \( \sqrt{2} \) | Square root of 2, a non-perfect square. | 1.41421... |
| \( \phi \) | Golden ratio. | 1.61803... |
Steps to Determine if a Number is Irrational
- Attempt to express the number as a fraction \( \frac{p}{q} \). If it is not possible, proceed to the next step.
- Convert the number to its decimal form.
- Check if the decimal expansion is non-terminating and non-repeating. If it is, the number is irrational.
Understanding irrational numbers is important as they play a critical role in various areas of mathematics, including algebra, calculus, and number theory. They help in comprehending the complexity and richness of the number system.
Understanding Square Roots
The concept of square roots is fundamental in mathematics, particularly in algebra and geometry. Here, we will explore what square roots are, how to calculate them, and their properties.
Definition of Square Roots
A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In other words, \( y \) is a square root of \( x \) if \( y \) multiplied by itself equals \( x \).
Notation
- The square root of a number \( x \) is denoted as \( \sqrt{x} \).
- For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
Properties of Square Roots
- Non-negative Result: The principal square root (denoted by \( \sqrt{} \)) of a non-negative number is always non-negative.
- Product Property: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \) for any non-negative numbers \( a \) and \( b \).
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for any non-negative numbers \( a \) and \( b \), with \( b \neq 0 \).
Calculating Square Roots
- Identify the number whose square root you want to find.
- Determine if the number is a perfect square (e.g., 1, 4, 9, 16, 25, etc.).
- If the number is a perfect square, find the integer whose square is the given number (e.g., \( \sqrt{25} = 5 \)).
- If the number is not a perfect square, use estimation or a calculator for an approximate value.
Examples of Square Roots
| Number | Square Root | Reasoning |
|---|---|---|
| 16 | 4 | \( 4 \times 4 = 16 \) |
| 25 | 5 | \( 5 \times 5 = 25 \) |
| 2 | \( \approx 1.414 \) | 1.414 is an approximation of \( \sqrt{2} \) |
| 50 | \( \approx 7.071 \) | 7.071 is an approximation of \( \sqrt{50} \) |
Understanding square roots is crucial as they are used in various mathematical computations and real-life applications, such as geometry, physics, and engineering.

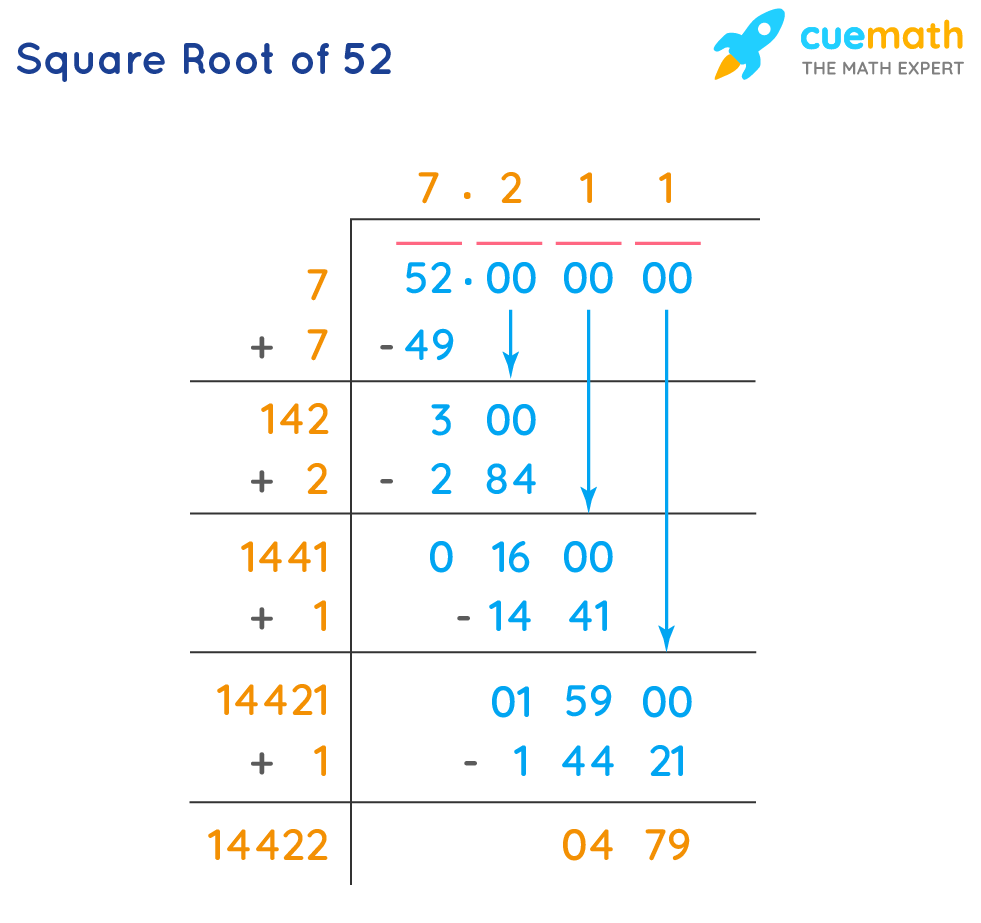
The Square Root of 25
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is a number which, when multiplied by itself, results in 25.
Mathematically, this can be represented as:
\[\sqrt{25} = x \]
where \(x \times x = 25\).
To find the square root of 25, we need to determine the number that, when squared, equals 25. We can perform the following steps:
- Identify the factors of 25. The number 25 can be expressed as \(5 \times 5\).
- Since \(5 \times 5 = 25\), we can conclude that the square root of 25 is 5.
Therefore, the square root of 25 is:
\[\sqrt{25} = 5\]
To verify this, we can square 5:
\[5 \times 5 = 25\]
This confirms that 5 is indeed the square root of 25.
In summary, the square root of 25 is 5, and since 5 is a whole number, it is a rational number.
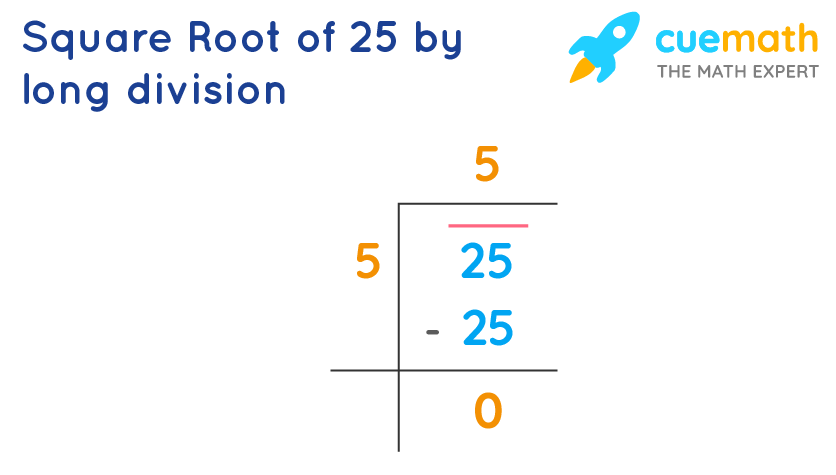
Calculating the Square Root of 25
To calculate the square root of 25, we follow a simple process. The square root of a number \( x \) is a value \( y \) such that \( y \times y = x \). In this case, we need to find \( y \) where:
\[\sqrt{25} = y\]
We can break down the calculation into the following steps:
- Identify the perfect square:
First, recognize that 25 is a perfect square, which means it can be expressed as the product of an integer with itself. Specifically, 25 can be written as:
\[25 = 5 \times 5\]
- Determine the square root:
Since \( 5 \times 5 = 25 \), we can deduce that the square root of 25 is:
\[\sqrt{25} = 5\]
- Verification:
To verify our result, we square the number we found to see if we get back to 25:
\[5 \times 5 = 25\]
The calculation confirms that 5 is indeed the square root of 25.
Thus, the square root of 25 is:
\[\sqrt{25} = 5\]
Since 5 is an integer, it is also a rational number. Rational numbers are numbers that can be expressed as a fraction or ratio of two integers, and since 5 can be written as \(\frac{5}{1}\), it fits this definition.
Properties of the Square Root of 25
The square root of 25 has several interesting properties that make it a notable example in mathematics. These properties highlight its classification as a rational number and its behavior in various mathematical contexts.
- Perfect Square: The number 25 is a perfect square, which means that it is the square of an integer. Specifically, 25 = 5^2, so the square root of 25 is 5.
- Rational Number: A rational number is defined as a number that can be expressed as the quotient or fraction of two integers. Since 5 can be written as 5/1, it is a rational number.
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. Therefore, the square roots of 25 are 5 and -5. Both are rational numbers.
- Non-Decimal Representation: The square root of 25 is an integer, which means it does not have a decimal or fractional component when expressed in its simplest form.
- Closure under Multiplication: The product of the square root of 25 with itself returns the original number: (√25) * (√25) = 25.
- Even Exponent Property: When 25 is raised to the power of 1/2 (the definition of the square root), it results in 5: 25^(1/2) = 5.
Understanding these properties helps in comprehending the nature of square roots and their classification within rational and irrational numbers.
Is the Square Root of 25 Rational?
The square root of 25 is indeed a rational number. To understand why, let's delve into the characteristics and proof of rationality for the square root of 25.
- Perfect Square: The number 25 is a perfect square because it can be written as \(5^2\). Therefore, the square root of 25 is 5, which is an integer.
- Definition of Rational Numbers: A rational number is any number that can be expressed as the quotient of two integers, where the denominator is not zero. In this case, 5 can be expressed as \(\frac{5}{1}\), which satisfies the condition of being a rational number.
- Prime Factorization Method: By prime factorizing 25, we get \(25 = 5 \times 5\). Taking the square root of both sides gives \(\sqrt{25} = \sqrt{5 \times 5} = 5\), confirming that the result is an integer and thus rational.
- Non-Decimal Representation: Since the square root of 25 is an integer (5), it does not have a non-terminating, non-repeating decimal expansion, which is characteristic of irrational numbers. Hence, it is rational.
- Verification through Methods: Various methods such as the long division method, repeated subtraction method, and geometric interpretation all confirm that the square root of 25 is 5, reinforcing its rationality.
In conclusion, the square root of 25 is a rational number because it meets all the criteria that define rational numbers, and its calculations consistently yield a whole number.

Is the Square Root of 25 Irrational?
The square root of 25 is not an irrational number. To understand why, let's examine the properties and definitions of rational and irrational numbers.
- Definition of Irrational Numbers: An irrational number is one that cannot be expressed as a fraction of two integers. It has a decimal expansion that neither terminates nor repeats.
- Perfect Squares: The number 25 is a perfect square, meaning it is the product of an integer multiplied by itself (5 × 5). The square root of a perfect square is always a whole number, which is rational.
- Square Root of 25: The square root of 25 is 5. Since 5 is an integer, it can be expressed as the fraction \(\frac{5}{1}\), which classifies it as a rational number.
- Mathematical Proof:
- Prime Factorization: The prime factorization of 25 is \(5 \times 5\). Taking the square root of both sides gives \(\sqrt{25} = \sqrt{5 \times 5} = 5\), an integer.
- Long Division Method: By using the long division method, we find that the square root of 25 is 5, with no remainder, further confirming it is an integer and thus rational.
- Decimal Representation: The square root of 25 is 5, which is a terminating decimal. Irrational numbers have non-terminating, non-repeating decimals, which is not the case here.
Therefore, the square root of 25 does not exhibit any properties of an irrational number. It is a rational number because it can be expressed as a simple fraction and has a terminating decimal representation.
Proof of Rationality
The square root of 25 is a rational number. Below are detailed steps and methods to prove its rationality:
- Definition of Rational Numbers: A rational number is any number that can be expressed as the quotient of two integers, where the denominator is not zero. In other words, if a number can be written in the form \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q \neq 0\), it is rational.
- Prime Factorization Method:
- First, factorize 25 into prime numbers: \(25 = 5 \times 5\).
- Take the square root of both sides: \(\sqrt{25} = \sqrt{5 \times 5} = 5\).
- Since 5 is an integer, it can be expressed as \(\frac{5}{1}\), which is a fraction of two integers. Thus, 5 is a rational number.
- Repeated Subtraction Method:
- Start with 25 and subtract consecutive odd numbers until you reach zero:
- 25 - 1 = 24
- 24 - 3 = 21
- 21 - 5 = 16
- 16 - 7 = 9
- 9 - 9 = 0
- Since it takes 5 subtractions to reach zero, the square root of 25 is 5.
- Long Division Method:
- Set up 25 for long division and find the largest number whose square is less than or equal to 25, which is 5.
- Subtract 25 from 25 to get a remainder of 0, confirming that \(\sqrt{25} = 5\).
- Geometric Method:
- Draw a square with an area of 25 square units.
- The side length of this square is the square root of 25, which is 5 units.
- Verification with Quadratic Equations:
- Consider the quadratic equation \(x^2 - 25 = 0\).
- Solving for \(x\) gives \(x = \pm \sqrt{25}\).
- Since \(\sqrt{25} = 5\), the solutions are \(x = \pm 5\), both of which are rational numbers.
Through these methods, we have confirmed that the square root of 25 is 5, which is a rational number. Each method provides a consistent and clear demonstration of this fact.
Examples of Rational Numbers
Rational numbers are numbers that can be expressed as the quotient of two integers, where the denominator is not zero. Here are some detailed examples of rational numbers:
- Integers: All integers are rational numbers because they can be expressed as a fraction with the denominator of 1.
- Example: 5 can be written as \(\frac{5}{1}\).
- Example: -3 can be written as \(\frac{-3}{1}\).
- Fractions: Any fraction where both the numerator and the denominator are integers and the denominator is not zero is a rational number.
- Example: \(\frac{1}{2}\) is a rational number.
- Example: \(\frac{-4}{5}\) is a rational number.
- Terminating Decimals: A decimal number that ends is a rational number because it can be converted to a fraction.
- Example: 0.75 is a rational number because it can be written as \(\frac{3}{4}\).
- Example: 0.5 is a rational number because it can be written as \(\frac{1}{2}\).
- Repeating Decimals: A decimal number that has a repeating pattern is also a rational number.
- Example: 0.333... (where 3 repeats) is a rational number because it can be written as \(\frac{1}{3}\).
- Example: 0.142857... (where 142857 repeats) is a rational number because it can be written as \(\frac{1}{7}\).
- Zero: Zero is a rational number because it can be expressed as a fraction where the numerator is zero and the denominator is a non-zero integer.
- Example: 0 can be written as \(\frac{0}{1}\).
These examples illustrate that rational numbers can take various forms, including whole numbers, fractions, and certain types of decimals. Understanding these examples helps in identifying and working with rational numbers in different mathematical contexts.
Examples of Irrational Numbers
Irrational numbers are real numbers that cannot be expressed as the quotient of two integers. They have non-terminating, non-repeating decimal expansions. Here are some detailed examples of irrational numbers:
- Pi (π): Pi is one of the most famous irrational numbers. It represents the ratio of the circumference of a circle to its diameter and is approximately 3.141592653589793... The decimal representation of Pi never ends and never repeats.
- Square Root of 2 (√2): The square root of 2 is another well-known irrational number. It cannot be precisely expressed as a fraction and its decimal expansion is approximately 1.4142135623730951..., continuing infinitely without repeating.
- Euler's Number (e): Euler's number, denoted as \(e\), is approximately 2.718281828459045... and is used extensively in mathematics, particularly in calculus. Like Pi, its decimal expansion is infinite and non-repeating.
- Golden Ratio (φ): The golden ratio, often denoted as φ (phi), is approximately 1.618033988749894... and appears in various areas of mathematics, art, and nature. Its decimal expansion also does not terminate or repeat.
- Square Root of Non-Perfect Squares: The square roots of numbers that are not perfect squares are irrational. Examples include:
- √3 ≈ 1.7320508075688772...
- √5 ≈ 2.23606797749979...
- √7 ≈ 2.6457513110645906...
- Cube Roots of Non-Perfect Cubes: The cube roots of numbers that are not perfect cubes are also irrational. Examples include:
- ∛2 ≈ 1.2599210498948732...
- ∛3 ≈ 1.4422495703074083...
These examples demonstrate that irrational numbers are prevalent in mathematics and have unique properties that distinguish them from rational numbers.
Importance of Understanding Rational and Irrational Numbers
Understanding the distinction between rational and irrational numbers is fundamental to the study of mathematics and has numerous practical applications. Here are several key reasons why it's important to grasp these concepts:
- Foundation of Number Theory: Rational and irrational numbers form the basis of number theory. This knowledge helps in understanding more complex mathematical concepts and theorems.
- Mathematical Problem Solving: Knowing whether a number is rational or irrational can simplify mathematical problem-solving and aid in selecting appropriate methods for computations and proofs.
- Real-Life Applications: Square roots, a common type of irrational number, appear in various real-life applications such as geometry, physics, engineering, and finance. For instance, the Pythagorean theorem uses square roots to determine distances.
- Precision and Approximation: Rational numbers can be precisely represented, which is crucial for tasks requiring exact measurements. In contrast, irrational numbers are often approximated, which is essential in fields like computer science and numerical analysis.
- Scientific Calculations: In science, calculations involving irrational numbers are common. Understanding their properties ensures accurate results in experiments and research.
- Technological Development: Advances in technology, particularly in computing, rely on a deep understanding of both rational and irrational numbers for developing algorithms and software that perform complex calculations efficiently.
- Educational Curriculum: Mastery of these concepts is part of the educational curriculum and is essential for students pursuing higher education in mathematics and related fields.
By understanding rational and irrational numbers, we enhance our mathematical literacy and problem-solving skills, which are valuable in both academic and real-world contexts.
Applications of Square Roots in Real Life
Square roots are not just abstract mathematical concepts; they have numerous practical applications in various fields. Here are some key areas where square roots play an essential role:
- Geometry and Trigonometry
Square roots are fundamental in geometry and trigonometry, particularly when calculating the lengths of sides in right-angled triangles using the Pythagorean theorem. For example, if a right-angled triangle has sides of length 3 and 4, the length of the hypotenuse is given by , which equals 5.
- Engineering and Construction
Engineers and architects use square roots to calculate dimensions and ensure structural integrity. For instance, determining the diagonal length of a rectangular frame involves using the square root to solve for the hypotenuse of a right-angled triangle formed by the length and width of the rectangle.
- Physics
In physics, square roots are used in various formulas. One common example is the calculation of the magnitude of vectors, such as velocity or force. The resultant vector's magnitude in a 2D space can be found using the square root of the sum of the squares of its components.
- Computer Graphics
Square roots are crucial in computer graphics for rendering realistic images. They are used in algorithms for lighting, shading, and distance calculations, which are essential for creating accurate and visually appealing scenes.
- Finance
In finance, square roots are used in risk management and option pricing models. For example, the Black-Scholes model for pricing options involves the square root of time in its volatility calculations, impacting the pricing of financial derivatives.
- Astronomy
Astronomers use square roots when calculating distances between celestial objects. For example, determining the distance between two stars involves the square root of the sum of the squares of the differences in their coordinates.
- Everyday Life
Even in everyday life, square roots find applications. For example, when determining the size of a TV screen, the diagonal length is calculated using the square root of the sum of the squares of the screen's width and height.
Conclusion
In conclusion, the square root of 25 is a rational number. This is because it can be expressed as the integer 5, which is a whole number. Rational numbers are those that can be written as a fraction or ratio of two integers, and since 5 can be expressed as 5/1, it qualifies as a rational number.
The understanding of rational and irrational numbers is fundamental in mathematics. Rational numbers include integers, finite decimals, and repeating decimals, all of which can be written as a ratio of two integers. On the other hand, irrational numbers cannot be expressed as a simple fraction and include non-repeating, non-terminating decimals such as the square root of 2, π (pi), and e (Euler's number).
Through various methods such as prime factorization, repeated subtraction, and using a calculator, we determined that the square root of 25 equals 5. This finding reinforces that 25 is a perfect square, as its square root is an integer. Understanding these concepts helps in many real-life applications, including geometry, engineering, and various scientific calculations where precise measurements are essential.
In summary, recognizing the square root of 25 as a rational number highlights the broader concept that the square roots of perfect squares are always rational. This knowledge is not only a crucial mathematical principle but also a practical tool for solving real-world problems.
Video này chứng minh rằng căn bậc hai của bất kỳ số nguyên nào cũng là vô tỷ, ngoại trừ các số chính phương. Khám phá lý thuyết toán học và các chứng minh cụ thể.
Bằng chứng rằng căn bậc hai của BẤT KỲ số nguyên nào cũng là vô tỷ (ngoại trừ các số chính phương)
READ MORE:
Video này giải thích về căn bậc hai của 25 và tại sao nó là một số hữu tỷ. Khám phá lý thuyết toán học đơn giản và dễ hiểu.
Căn bậc hai của 25