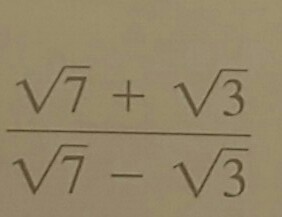Square Root 3 Symbol: Understanding and Using This Mathematical Constant

The square root of 3 is an important mathematical constant, often represented in various forms in mathematical notation. Below is the symbol for the square root of 3 using MathJax:

\(\sqrt{3}\)

Mathematical Representation

The square root of 3 is written as:

\(\sqrt{3}\)

In LaTeX or MathJax, you can represent this symbol by using the following code:

\(\sqrt{3}\)

Decimal Approximation

The square root of 3 is approximately equal to 1.732. It is an irrational number, meaning its decimal representation goes on forever without repeating.

\(\sqrt{3} \approx 1.732\)

Usage in Geometry

The square root of 3 frequently appears in geometry, particularly in the context of equilateral triangles. For instance, the height of an equilateral triangle with side length \(a\) can be calculated as:

\(\text{Height} = \frac{\sqrt{3}}{2}a\)

Importance in Mathematics

• The square root of 3 is crucial in various mathematical fields, including algebra, trigonometry, and calculus.
• It is commonly used in solving equations involving quadratic forms and in calculating distances in Euclidean space.

Additional Information

For more complex mathematical expressions involving the square root of 3, you can combine it with other LaTeX symbols. For example:

\(\frac{\sqrt{3}}{2}\)

Using the above code in a MathJax-enabled environment will render the fraction with the square root of 3 in the numerator.

The square root of 3, denoted as \(\sqrt{3}\), is an important mathematical constant approximately equal to 1.732. It is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal expansion is non-repeating and non-terminating.

In mathematics, the square root of 3 is used in various fields such as geometry, algebra, and trigonometry. Understanding this constant is essential for solving a variety of mathematical problems. Here are some key points about the square root of 3:

• Geometric Significance: In an equilateral triangle, the height can be calculated using \(\sqrt{3}\). For a triangle with side length \(a\), the height is \(\frac{\sqrt{3}}{2}a\).
• Algebraic Importance: The square root of 3 often appears in solutions to quadratic equations and polynomial expressions.
• Trigonometric Applications: In trigonometry, \(\sqrt{3}\) is found in the values of certain trigonometric functions, such as \(\tan(60^\circ) = \sqrt{3}\).

To represent the square root of 3 in mathematical notation, MathJax or LaTeX can be used. For example:

\(\sqrt{3}\)

To display it in LaTeX, you would write:

\(\sqrt{3}\)

Overall, the square root of 3 is a fundamental component in many mathematical concepts and its understanding is crucial for deeper insights into various mathematical theories and applications.

The square root of 3, represented as \( \sqrt{3} \), plays a significant role in geometry, particularly in relation to equilateral triangles and hexagons. Here, we explore its geometric implications and applications.

Equilateral Triangle

An equilateral triangle has all three sides of equal length and all internal angles measuring 60 degrees. The height (altitude) of an equilateral triangle can be determined using \( \sqrt{3} \).

• Let each side of the equilateral triangle be \( a \).
• The altitude divides the triangle into two 30-60-90 right triangles.
• In a 30-60-90 triangle, the ratio of the sides is 1 : \( \sqrt{3} \) : 2.
• Therefore, the altitude (height) \( h \) is given by \( h = \frac{\sqrt{3}}{2}a \).

Thus, the height of an equilateral triangle is proportional to the square root of 3, making it essential for calculating area and understanding the triangle's properties.

Hexagon

A regular hexagon can be divided into six equilateral triangles. This connection highlights the importance of \( \sqrt{3} \) in hexagonal geometry.

• Let the side length of the hexagon be \( a \).
• The distance from the center to any vertex (radius) is equal to the side length \( a \).
• The distance from the center to the midpoint of any side (apothem) is \( \frac{\sqrt{3}}{2}a \).

The apothem is crucial for calculating the area of the hexagon, which is given by:

\[ \text{Area} = \frac{1}{2} \times \text{Perimeter} \times \text{Apothem} \]

Therefore, the area of the hexagon can be expressed as:

\[ \text{Area} = \frac{1}{2} \times 6a \times \frac{\sqrt{3}}{2}a = 3\sqrt{3}a^2 \]

Pythagorean Theorem

In right-angled triangles, \( \sqrt{3} \) emerges in various applications. For instance, in a 30-60-90 triangle, where one angle is 30 degrees and the other is 60 degrees:

• The side opposite the 60-degree angle is \( \sqrt{3} \) times the side opposite the 30-degree angle.

This ratio is crucial for solving problems involving right-angled triangles and understanding their geometric properties.

Summary

The square root of 3 is fundamental in geometric contexts, particularly in equilateral triangles and hexagons. Its presence in the side ratios and areas of these shapes underscores its importance in geometry.

The square root of 3, represented as \( \sqrt{3} \), is frequently encountered in algebraic equations and expressions. Here, we explore its various applications in algebra, illustrating its importance in solving problems and understanding algebraic concepts.

Quadratic Equations

Quadratic equations often involve roots that include \( \sqrt{3} \). For example, consider the equation:

\[ x^2 - 3 = 0 \]

To solve this equation, we can isolate \( x^2 \):

\[ x^2 = 3 \]

Taking the square root of both sides, we get:

\[ x = \pm \sqrt{3} \]

Thus, the solutions to the equation are \( x = \sqrt{3} \) and \( x = -\sqrt{3} \).

Factoring Expressions

The square root of 3 is useful in factoring algebraic expressions. For instance, consider the polynomial:

\[ x^2 - 2x\sqrt{3} + 3 \]

This can be factored as:

\[ (x - \sqrt{3})^2 \]

Such factorizations are essential for simplifying expressions and solving polynomial equations.

Solving Systems of Equations

The square root of 3 also appears in systems of equations. For example:

\[ \begin{cases} x + y = \sqrt{3} \\ x - y = \sqrt{3} \end{cases} \]

To solve this system, we can add the two equations:

\[ (x + y) + (x - y) = 2x = 2\sqrt{3} \]

Thus:

\[ x = \sqrt{3} \]

Substituting \( x \) back into one of the original equations, we get:

\[ \sqrt{3} + y = \sqrt{3} \]

Thus:

\[ y = 0 \]

The solution to the system is \( (x, y) = (\sqrt{3}, 0) \).

Complex Numbers

In the realm of complex numbers, \( \sqrt{3} \) plays a significant role. Consider a complex number in the form \( a + bi \), where \( a \) and \( b \) are real numbers and \( i \) is the imaginary unit. The modulus of the complex number \( 1 + \sqrt{3}i \) is given by:

\[ |1 + \sqrt{3}i| = \sqrt{1^2 + (\sqrt{3})^2} = \sqrt{1 + 3} = 2 \]

This demonstrates how \( \sqrt{3} \) is integral in calculating the modulus of complex numbers.

Summary

The square root of 3 is pervasive in algebra, from solving quadratic equations and factoring expressions to tackling systems of equations and working with complex numbers. Its presence underscores its importance in various algebraic contexts.

The square root of 3, represented as \( \sqrt{3} \), plays a crucial role in trigonometry. It appears in the values of trigonometric functions for specific angles and is fundamental in various trigonometric identities and equations.

Some key aspects of its trigonometric importance include:

• Exact Values for Specific Angles:

  For example, \( \sqrt{3} \) is seen in the exact values of trigonometric functions at 30° (or \( \frac{\pi}{6} \) radians) and 60° (or \( \frac{\pi}{3} \) radians).

  • \(\sin(60^\circ) = \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}\)
  • \(\cos(30^\circ) = \cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\)
  • \(\tan(60^\circ) = \tan\left(\frac{\pi}{3}\right) = \sqrt{3}\)
  • \(\cot(30^\circ) = \cot\left(\frac{\pi}{6}\right) = \sqrt{3}\)
• Trigonometric Identities:

  It is also essential in forming and simplifying various trigonometric identities. For example:

  • \(\sin(2\theta) = 2 \sin(\theta) \cos(\theta)\)
  • \(\tan(3\theta) = \frac{3\tan(\theta) - \tan^3(\theta)}{1 - 3\tan^2(\theta)}\)
• Law of Sines and Cosines:

  The square root of 3 appears in applications of the Law of Sines and the Law of Cosines, especially in problems involving 30-60-90 triangles. In a 30-60-90 triangle:

  • The side opposite the 30° angle is \( \frac{1}{2} \) the hypotenuse.
  • The side opposite the 60° angle is \( \frac{\sqrt{3}}{2} \) the hypotenuse.
• Complex Numbers and Euler's Formula:

  In complex numbers, \( \sqrt{3} \) is often part of Euler's formula and its applications:

  • Euler's Formula: \( e^{i\theta} = \cos(\theta) + i\sin(\theta) \)
  • For \( \theta = \frac{\pi}{3} \): \( e^{i\frac{\pi}{3}} = \frac{1}{2} + i\frac{\sqrt{3}}{2} \)

The square root of 3, denoted as \( \sqrt{3} \), plays a significant role in various branches of calculus and advanced mathematics. Below are some detailed insights into its applications and importance:

• Differentiation and Integration:

  In calculus, functions involving \( \sqrt{3} \) often appear in differentiation and integration problems. For example, consider the function \( f(x) = \sqrt{3}x^2 \). The derivative of this function with respect to \( x \) is:

  \[
  f'(x) = \frac{d}{dx}(\sqrt{3}x^2) = 2\sqrt{3}x
  \]

  Similarly, the integral of a function involving \( \sqrt{3} \) can be expressed as:

  \[
  \int \sqrt{3}x \, dx = \sqrt{3} \int x \, dx = \sqrt{3} \cdot \frac{x^2}{2} + C = \frac{\sqrt{3}}{2} x^2 + C
  \]

• Series Expansion:

  In advanced mathematics, \( \sqrt{3} \) is often encountered in the series expansion of functions. For example, the exponential function \( e^{\sqrt{3}x} \) can be expanded as a Taylor series:

  \[
  e^{\sqrt{3}x} = \sum_{n=0}^{\infty} \frac{(\sqrt{3}x)^n}{n!} = 1 + \sqrt{3}x + \frac{(\sqrt{3}x)^2}{2!} + \frac{(\sqrt{3}x)^3}{3!} + \cdots
  \]

• Limits and Continuity:

  In calculus, evaluating limits involving \( \sqrt{3} \) is a common exercise. For instance, the limit as \( x \) approaches 0 for the function \( \sqrt{3} \sin(x) \) is:

  \[
  \lim_{x \to 0} \sqrt{3} \sin(x) = \sqrt{3} \cdot 0 = 0
  \]

• Roots of Equations:

  Finding the roots of equations is another area where \( \sqrt{3} \) is frequently encountered. For instance, the quadratic equation \( x^2 - 3 = 0 \) has solutions \( x = \pm \sqrt{3} \).

• Complex Numbers:

  In complex analysis, \( \sqrt{3} \) often appears in the context of complex numbers and polar coordinates. The complex number \( 1 + \sqrt{3}i \) can be expressed in polar form as:

  \[
  1 + \sqrt{3}i = 2 \left( \cos\left(\frac{\pi}{3}\right) + i \sin\left(\frac{\pi}{3}\right) \right)
  \]

Overall, the square root of 3 is an essential constant that appears in numerous mathematical contexts, from basic algebra to advanced calculus and beyond.

The square root of 3, denoted as \(\sqrt{3}\), has numerous applications in various fields, ranging from engineering to natural sciences. Here are some of the most significant real-world applications:

• Engineering and Construction:

  The square root of 3 is crucial in the design and analysis of structures. It appears in the calculations of forces in equilateral triangles, which are common in truss systems used in bridges and roofs.

  Application	Description
  Truss Systems	Used to calculate forces in members of a truss with equilateral triangle formations.

• Electrical Engineering:

  In electrical engineering, the square root of 3 is used in the analysis of three-phase power systems. The relationship between line-to-line voltage and line-to-neutral voltage in a balanced three-phase system involves \(\sqrt{3}\).

  • Three-phase power calculation: V_{LL} = \sqrt{3} \times V_{LN}
• Geometry:

  In geometry, the square root of 3 is essential in calculations involving 30-60-90 triangles. These triangles have side ratios of 1 : \(\sqrt{3}\) : 2.

  1. Height of an equilateral triangle: h = \frac{\sqrt{3}}{2} \times \text{side length}
• Physics:

  The square root of 3 appears in various physics problems, including those related to wave interference and the crystallography of certain materials.

  • Wave interference patterns: Used to calculate path differences in wave phenomena.
• Robotics:

  In robotics, the square root of 3 is used in the kinematics of robotic arms, especially those designed with equilateral triangular configurations for stability and precision.

• Telecommunications:

  In telecommunications, \(\sqrt{3}\) is used in the modulation and demodulation of signals, as well as in the analysis of signal strength and interference patterns.

The concept of square roots, including the square root of 3, has a rich history that spans across various ancient civilizations. The understanding and calculation of square roots have been documented in several key historical texts and artifacts.

Babylonian Mathematics:

• One of the earliest known records of square roots is found on a Babylonian clay tablet (YBC 7289), dated between 1800 BC and 1600 BC. This tablet shows the calculations of square roots using a sexagesimal (base-60) number system.

Ancient Egyptian Mathematics:

• The Rhind Mathematical Papyrus, dating back to around 1650 BC, includes methods for calculating square roots. These methods were part of practical arithmetic techniques used by the Egyptians.

Indian Mathematics:

• In Ancient India, texts such as the Sulba Sutras (800-500 BC) provided geometric and arithmetic rules, including methods for finding square roots. The Baudhayana Sulba Sutra, for instance, gives approximations for the square roots of 2 and 3.
• Aryabhata, in his work Aryabhatiya (circa 499 AD), developed algorithms for extracting square roots, demonstrating the advanced mathematical understanding of ancient Indian scholars.

Greek Mathematics:

• The ancient Greeks also explored square roots. The discovery of irrational numbers, including the square root of 2, is attributed to the Pythagoreans. Theaetetus, a student of Plato, extended this understanding to show that the square roots of non-square integers are irrational.

Medieval Islamic Mathematics:

• Islamic mathematicians preserved and expanded upon the mathematical knowledge of earlier civilizations. Al-Khwarizmi, in the 9th century, wrote about algebra and methods to solve quadratic equations, which included finding square roots.

Through these historical milestones, the concept of the square root of 3 has evolved and contributed to various fields of mathematics, influencing subsequent developments in algebra, geometry, and calculus.

The square root of 3, often denoted as \( \sqrt{3} \), is an important mathematical constant that appears in various number systems. Its value is approximately 1.732, but it holds unique characteristics across different number systems. Here, we explore the representation and significance of \( \sqrt{3} \) in different contexts:

Real Numbers

In the real number system, \( \sqrt{3} \) is an irrational number. This means it cannot be expressed as a simple fraction, and its decimal representation is non-terminating and non-repeating. This property is crucial in many mathematical and real-world applications, particularly in geometry and trigonometry.

Rational Numbers

Rational numbers are those that can be expressed as a ratio of two integers. Since \( \sqrt{3} \) cannot be expressed as such a ratio, it is classified as an irrational number. Its approximate value can be used in rational approximations for practical calculations.

Complex Numbers

In the complex number system, \( \sqrt{3} \) can be used in conjunction with imaginary numbers. For example, the expression \( \sqrt{-3} \) is represented as \( \sqrt{3}i \), where \( i \) is the imaginary unit.

Decimal and Fractional Representations

While \( \sqrt{3} \) is irrational, it can be approximated by decimal fractions for practical purposes. For instance, \( \sqrt{3} \approx 1.732 \). Such approximations are useful in engineering and science where exact values are less critical than functional ones.

Geometric Significance

In geometry, \( \sqrt{3} \) appears frequently, especially in problems involving equilateral triangles. The height of an equilateral triangle with side length \( a \) is \( \frac{\sqrt{3}}{2}a \). This relationship is foundational in many geometric constructions and proofs.

Algebraic Context

In algebra, \( \sqrt{3} \) often appears in solutions to quadratic equations. For example, the roots of the equation \( x^2 - 3 = 0 \) are \( \pm \sqrt{3} \). Understanding these roots is essential for solving polynomial equations.

Visualization in the Coordinate Plane

On the coordinate plane, the distance between points can involve \( \sqrt{3} \). For example, the distance between points (0, 0) and (1, \( \sqrt{3} \)) is exactly 2 units, illustrating the Pythagorean theorem.

Understanding the role of \( \sqrt{3} \) across different number systems enhances our comprehension of its properties and applications, making it a vital part of mathematical studies.

The square root of 3, denoted as \( \sqrt{3} \), can be visualized and represented graphically in various ways. These visualizations help in understanding its properties and applications better.

Number Line Representation

One of the simplest ways to visualize \( \sqrt{3} \) is by locating it on a number line. Since \( \sqrt{3} \) is approximately 1.732, it lies between 1 and 2 on the number line. By constructing a right triangle with legs of 1 unit each, the hypotenuse will represent \( \sqrt{2} \). Similarly, for \( \sqrt{3} \), one can use the Pythagorean theorem in a more complex geometric construction.

Geometric Visualization

Geometrically, \( \sqrt{3} \) often appears in the context of equilateral triangles. For an equilateral triangle with side length 2, the altitude (height) can be calculated using the Pythagorean theorem:

\[
\text{Altitude} = \sqrt{2^2 - 1^2} = \sqrt{4 - 1} = \sqrt{3}
\]

This altitude visually represents \( \sqrt{3} \) in a 2-dimensional geometric shape.

Graphical Representation

Using graphing tools like Desmos or graphing calculators, \( \sqrt{3} \) can be represented on various graphs:

• Quadratic Graphs: Consider the equation \( y = x^2 - 3 \). The points where the parabola intersects the x-axis are \( x = \pm\sqrt{3} \).
• Circle Graphs: A circle with radius \( \sqrt{3} \) centered at the origin can be plotted with the equation \( x^2 + y^2 = 3 \).

Complex Plane Representation

In the complex plane, \( \sqrt{3} \) can be part of a complex number. For instance, consider the complex number \( 1 + \sqrt{3}i \). Its graphical representation is a point in the complex plane, lying at coordinates (1, \( \sqrt{3} \)).

Moreover, visualizing roots of equations such as \( x^2 + 3 = 0 \) involves plotting the imaginary roots \( x = \pm \sqrt{3}i \) on the complex plane, giving insight into the symmetry and nature of these solutions.

Examples Using Graphing Calculators

Graphing calculators and tools like Desmos allow interactive exploration of \( \sqrt{3} \). For instance:

• Plotting \( y = \sqrt{3} \) as a constant function shows a horizontal line at \( y = \sqrt{3} \).
• Visualizing equations like \( y = x \sqrt{3} \) or \( y = \sqrt{3} x^2 \) demonstrates how \( \sqrt{3} \) scales and modifies standard functions.

These graphical representations are crucial for better understanding and interpreting the mathematical properties and applications of \( \sqrt{3} \).

There are several common misconceptions related to the square root of 3 and square roots in general. Understanding these can help clarify the true nature of square roots and their properties.

• Misconception 1: The Square Root of a Number Always Has Two Values

  Many believe that the square root of a number, such as √3, has two values: a positive and a negative. However, the principal square root symbol (√) denotes only the non-negative value. Therefore, √3 is approximately 1.732, not ±1.732. The notation ± is used in solving equations like \(x^2 = 9\), leading to solutions \(x = ±3\).

• Misconception 2: The Square Root of a Negative Number is Undefined

  While it is true that the square root of a negative number is not a real number, in the realm of complex numbers, it is defined. For example, the square root of -3 is represented as √(-3) = √3 * i, where i is the imaginary unit. This allows for meaningful operations and solutions in advanced mathematics.

• Misconception 3: √(a * b) = √a * √b for All a and b

  This property holds true only when both a and b are non-negative. For example, √(9 * 4) = √9 * √4 = 3 * 2 = 6. However, for negative values, this rule does not apply directly without involving complex numbers. For instance, √(-9 * -4) = √36 = 6, not √(-9) * √(-4) which would be 3i * 2i = -6.

• Misconception 4: The Square Root Function is the Inverse of the Squaring Function

  This is only partially true. The square root function is the inverse of the squaring function over the non-negative reals. For example, the squaring function takes 3 and maps it to 9, and the square root function takes 9 and maps it back to 3. However, the squaring function \(x^2\) maps both 3 and -3 to 9, while the square root function √9 only returns the non-negative root, 3.

By recognizing and addressing these misconceptions, we can gain a clearer and more accurate understanding of mathematical principles related to square roots.

• What is the square root symbol?

  The square root symbol, also known as the radical, is denoted by the symbol \( \sqrt{} \). It is used to represent the square root of a number.

• What is the square root of 3?

  The square root of 3 is represented as \( \sqrt{3} \). It is an irrational number approximately equal to 1.732.

• Why is the square root of 3 important?

  The square root of 3 is important in various fields such as geometry, trigonometry, and physics. It appears in the calculation of heights in equilateral triangles and in the sine and cosine functions for 30° and 60° angles.

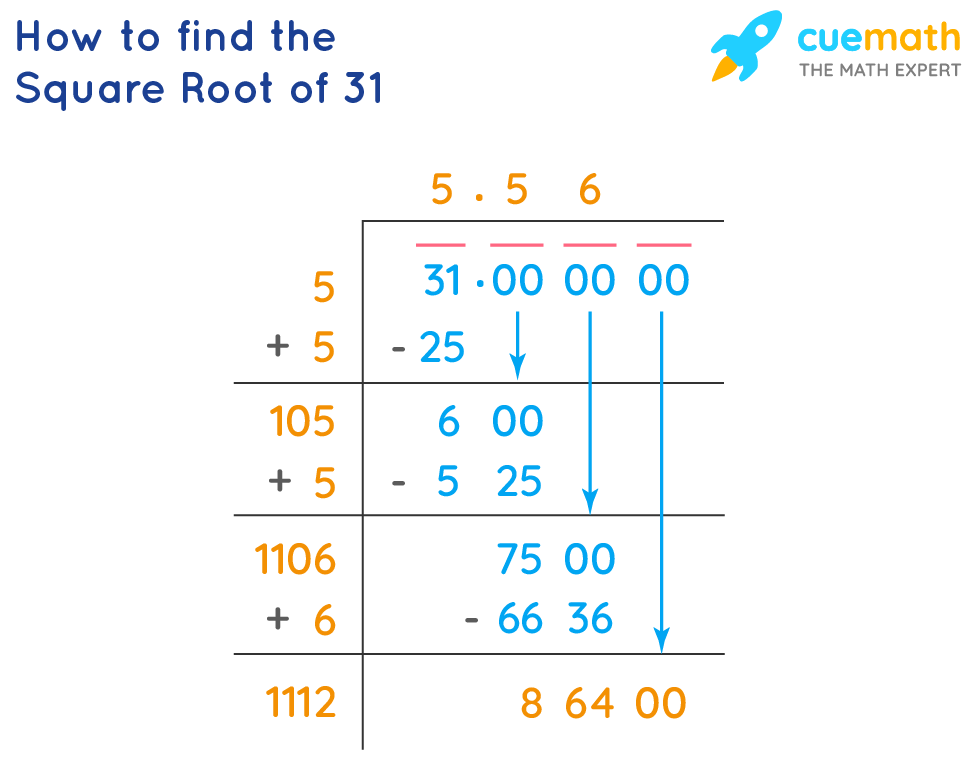
• How do you calculate the square root of 3?

  Calculating the square root of 3 can be done using a calculator with a square root function. Alternatively, it can be approximated using numerical methods such as the Newton-Raphson method.

• Is the square root of 3 a rational number?

  No, the square root of 3 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal expansion is non-terminating and non-repeating.

• What are some common misconceptions about the square root of 3?

  A common misconception is that the square root of a number can be negative. While solving equations like \( x^2 = 9 \) might yield \( x = \pm3 \), the square root function \( \sqrt{9} \) is defined to be the principal (positive) root, which is 3.

• How is the square root of 3 used in geometry?

  In geometry, the square root of 3 is often used in problems involving equilateral triangles, where the height of the triangle can be expressed as \( \frac{\sqrt{3}}{2} \) times the side length.

• What is the historical significance of the square root of 3?

  The square root of 3 has been known and used since ancient times. It appears in the geometry of ancient Greek and Indian mathematicians who studied the properties of triangles and circles.

For further reading and exploration of the square root of 3, consider the following resources:

• An extensive article covering the mathematical properties, history, and applications of the square root of 3.

• A comprehensive resource that includes mathematical details, proofs, and applications related to the square root of 3.

• An online calculator that can help you compute the square root of any number, including 3, with step-by-step solutions.

• A beginner-friendly introduction to square roots, including videos and practice exercises to solidify understanding.

• Detailed explanations and examples on how to work with radicals and square roots, including the square root of 3.

These resources provide a range of information from basic understanding to advanced mathematical concepts involving the square root of 3.