Topic square root of 252 simplified: Understanding the square root of 252 can be simple with our step-by-step guide. This article breaks down the process of simplifying the square root of 252, making it easy to grasp for anyone. Perfect for students and math enthusiasts, discover how to simplify and apply this concept effortlessly.
Table of Content
- Square Root of 252 Simplified
- Introduction
- Understanding Square Roots
- Prime Factorization of 252
- Breaking Down the Square Root of 252
- Step-by-Step Simplification Process
- Expressing the Result in Simplest Form
- Mathematical Properties of Square Roots
- Applications of Square Roots in Real Life
- Common Mistakes to Avoid
- Practice Problems
- Conclusion
- YOUTUBE:
Square Root of 252 Simplified
The square root of 252 can be simplified by expressing 252 as a product of its prime factors and then simplifying the square root.
Step-by-Step Simplification
- Find the prime factorization of 252:
- 252 = 2 × 126
- 126 = 2 × 63
- 63 = 3 × 21
- 21 = 3 × 7
- Therefore, 252 = 2^2 × 3^2 × 7
- Write the square root of 252 using its prime factors:
\(\sqrt{252} = \sqrt{2^2 \times 3^2 \times 7}\)
- Separate the perfect squares from the non-perfect squares:
\(\sqrt{252} = \sqrt{(2^2) \times (3^2) \times 7}\)
- Simplify the square root by taking the square root of the perfect squares:
\(\sqrt{252} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{7}\)
\(\sqrt{252} = 2 \times 3 \times \sqrt{7}\)
\(\sqrt{252} = 6\sqrt{7}\)
Therefore, the simplified form of the square root of 252 is \(6\sqrt{7}\).

READ MORE:
Introduction
Simplifying the square root of 252 involves breaking it down into its prime factors and reducing it to its simplest form. This process is essential for understanding how to handle square roots in algebra and higher-level mathematics. In this guide, we will take you through the step-by-step method to simplify \(\sqrt{252}\), making it easier to comprehend and apply in various mathematical problems.
- First, identify the prime factors of 252.
- Then, express 252 as a product of these prime factors.
- Next, group the prime factors into pairs.
- Take the square root of each pair and simplify the expression.
By following these steps, we will transform \(\sqrt{252}\) into a more manageable and understandable form. This foundational skill is crucial for students, educators, and anyone interested in mastering mathematics.
Understanding Square Roots
The concept of square roots is fundamental in mathematics, particularly in algebra and geometry. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 multiplied by 3 equals 9.
Mathematically, the square root of a number \( n \) is denoted as \( \sqrt{n} \). The principal square root is the non-negative root of a non-negative number.
Here are some important points to understand about square roots:
- Positive and Negative Roots: While the principal square root of a number is usually considered positive, every positive number actually has two square roots: one positive and one negative. For example, the square roots of 16 are 4 and -4.
- Square Root of Zero: The square root of 0 is 0 because 0 multiplied by itself is still 0.
- Square Roots of Negative Numbers: Negative numbers do not have real square roots because no real number squared gives a negative result. Instead, they have imaginary square roots, involving the imaginary unit \( i \) where \( i = \sqrt{-1} \).
Square roots can also be understood through the concept of exponents. The square root of a number \( n \) is equivalent to raising \( n \) to the power of \( \frac{1}{2} \). This can be expressed as:
\[
\sqrt{n} = n^{\frac{1}{2}}
\]
To summarize, understanding square roots involves recognizing their properties, their relationship with exponents, and their application in solving various mathematical problems.
Prime Factorization of 252
Prime factorization is the process of breaking down a composite number into a product of its prime factors. To find the prime factorization of 252, we will divide it by the smallest prime numbers until we are left with only prime numbers. Let's go through this step by step.
- Divide by 2: Since 252 is even, we start by dividing it by 2.
\[
252 \div 2 = 126
\] - Divide by 2 again: 126 is also even, so we divide it by 2 again.
\[
126 \div 2 = 63
\] - Divide by 3: The number 63 is not even, so we move to the next smallest prime number, which is 3. Since 63 is divisible by 3, we divide it by 3.
\[
63 \div 3 = 21
\] - Divide by 3 again: 21 is also divisible by 3, so we divide it by 3 again.
\[
21 \div 3 = 7
\] - Divide by 7: Finally, 7 is a prime number, so we have completed the factorization.
Putting it all together, the prime factorization of 252 is:
\[
252 = 2 \times 2 \times 3 \times 3 \times 7
\]
This can also be written in exponential form as:
\[
252 = 2^2 \times 3^2 \times 7
\]
Prime factorization is a useful technique for simplifying square roots, finding the greatest common divisors, and solving various other mathematical problems.
Breaking Down the Square Root of 252
To break down the square root of 252, we will use its prime factorization. The prime factorization of 252 is:
\[
252 = 2^2 \times 3^2 \times 7
\]
We can use this factorization to simplify the square root. The square root of a product is equal to the product of the square roots of the factors. Therefore, we have:
\[
\sqrt{252} = \sqrt{2^2 \times 3^2 \times 7}
\]
We know that the square root of a square number is just the base of the exponent. Hence:
\[
\sqrt{2^2 \times 3^2 \times 7} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{7}
\]
\[
\sqrt{2^2} = 2, \quad \sqrt{3^2} = 3, \quad \text{and} \quad \sqrt{7} \text{ remains as it is because 7 is not a perfect square.}
\]
So, we can simplify further:
\[
\sqrt{252} = 2 \times 3 \times \sqrt{7}
\]
\[
2 \times 3 = 6
\]
Thus, we have:
\[
\sqrt{252} = 6\sqrt{7}
\]
Therefore, the square root of 252 simplified is \( 6\sqrt{7} \). This process shows how prime factorization helps in breaking down and simplifying the square root of a number.

Step-by-Step Simplification Process
To simplify the square root of 252, we will break it down using prime factorization and then simplify the radical expression.
- First, find the prime factorization of 252.
- 252 ÷ 2 = 126
- 126 ÷ 2 = 63
- 63 ÷ 3 = 21
- 21 ÷ 3 = 7
- 7 ÷ 7 = 1
- Express the square root of 252 using its prime factors.
- Use the property of square roots that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Simplify the square roots of the perfect squares.
- Multiply the numbers outside the square root.
- Verify the simplified form.
252 can be factored into prime numbers as follows:
So, the prime factorization of 252 is \( 2^2 \times 3^2 \times 7 \).
We can write:
\[
\sqrt{252} = \sqrt{2^2 \times 3^2 \times 7}
\]
Applying this property, we get:
\[
\sqrt{252} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{7}
\]
Since \( \sqrt{2^2} = 2 \) and \( \sqrt{3^2} = 3 \), we can simplify the expression to:
\[
\sqrt{252} = 2 \times 3 \times \sqrt{7}
\]
Multiply \( 2 \times 3 \) to get 6, giving us:
\[
\sqrt{252} = 6 \sqrt{7}
\]
The simplified form of the square root of 252 is \( 6 \sqrt{7} \).
This step-by-step process shows how the square root of 252 simplifies to \( 6 \sqrt{7} \). Understanding this process allows for a better grasp of how to simplify other square roots as well.
Expressing the Result in Simplest Form
After simplifying the square root of 252, we need to express it in its simplest form. Let’s review the process to ensure that the expression is fully simplified.
- Identify the simplified form from the previous step.
- Verify the components of the simplified form.
- Check for further simplification.
- Confirm the simplest form.
- Final expression.
From our earlier simplification, we found:
\[
\sqrt{252} = 6 \sqrt{7}
\]
We expressed \( \sqrt{252} \) as a product of a whole number and a square root. In this case, the whole number is 6 and the square root component is \( \sqrt{7} \).
Examine \( \sqrt{7} \) to see if it can be simplified further. Since 7 is a prime number, \( \sqrt{7} \) is already in its simplest form and cannot be simplified further.
Since both 6 and \( \sqrt{7} \) are in their simplest forms and there are no common factors to extract or simplify further, the expression \( 6 \sqrt{7} \) is indeed the simplest form of \( \sqrt{252} \).
Thus, we express the square root of 252 in its simplest form as:
\[
\sqrt{252} = 6 \sqrt{7}
\]
This is the most simplified version of the square root of 252. By expressing it this way, we ensure clarity and precision in mathematical communication.
Mathematical Properties of Square Roots
Understanding the mathematical properties of square roots is essential for simplifying and working with radical expressions. Here, we explore key properties that are fundamental when dealing with square roots.
- Non-Negative Property
- Product Property
- Quotient Property
- Power Property
- Combining Like Radicals
- Rationalizing the Denominator
The square root of a non-negative number is always non-negative. This is because the square root operation is defined as the non-negative value that, when squared, returns the original number.
\[
\sqrt{x} \geq 0 \quad \text{for all} \quad x \geq 0
\]
The square root of a product is equal to the product of the square roots of the individual factors. This property allows us to simplify complex square roots by breaking them down into smaller components.
\[
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\]
Example: \( \sqrt{252} = \sqrt{4 \times 63} = \sqrt{4} \times \sqrt{63} = 2 \times \sqrt{63} \).
The square root of a quotient is the quotient of the square roots of the numerator and the denominator. This property is particularly useful when simplifying fractions under a square root.
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \quad \text{for} \quad b \neq 0
\]
Example: \( \sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} \).
The square root of a number raised to a power can be simplified using the property of exponents. Specifically, the square root of \( x^2 \) is \( x \) for non-negative values of \( x \).
\[
\sqrt{x^2} = |x|
\]
Example: \( \sqrt{3^2} = 3 \).
Radicals can be combined or simplified if they have the same radicand (the number inside the square root). This is similar to combining like terms in algebra.
\[
a \sqrt{b} + c \sqrt{b} = (a + c) \sqrt{b}
\]
Example: \( 2 \sqrt{5} + 3 \sqrt{5} = 5 \sqrt{5} \).
To simplify expressions with square roots in the denominator, we use the process of rationalization, which involves multiplying by a conjugate or a suitable term to remove the radical from the denominator.
\[
\frac{a}{\sqrt{b}} \times \frac{\sqrt{b}}{\sqrt{b}} = \frac{a \sqrt{b}}{b}
\]
Example: \( \frac{5}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{5 \sqrt{2}}{2} \).
These properties are essential tools for simplifying, calculating, and understanding expressions involving square roots. Mastering them can make solving complex mathematical problems more manageable.
Applications of Square Roots in Real Life
Square roots are fundamental in mathematics and appear in various real-life applications across different fields. Below are some key areas where square roots play a vital role.
- Geometry and Architecture
- Physics and Engineering
- Financial Modeling
- Computer Graphics and Animation
- Medicine and Pharmacology
- Acoustics and Signal Processing
- Astronomy
In geometry, square roots are used to calculate distances, areas, and other measurements. For instance, the Pythagorean theorem uses square roots to find the length of the hypotenuse in a right triangle:
\[
c = \sqrt{a^2 + b^2}
\]
Architects use these principles to design buildings and structures, ensuring accurate measurements and stability.
Square roots are essential in physics and engineering calculations. They are used to determine magnitudes, speeds, and forces. For example, the formula for the period of a pendulum involves a square root:
\[
T = 2 \pi \sqrt{\frac{L}{g}}
\]
where \( T \) is the period, \( L \) is the length of the pendulum, and \( g \) is the acceleration due to gravity.
In finance, square roots are used in models for calculating volatility and risks. For example, the standard deviation, a measure of financial risk, involves square roots:
\[
\sigma = \sqrt{\frac{\sum_{i=1}^n (x_i - \mu)^2}{n}}
\]
where \( \sigma \) is the standard deviation, \( x_i \) are data points, \( \mu \) is the mean, and \( n \) is the number of data points.
In computer graphics, square roots are used to calculate distances between points and to normalize vectors. This is crucial for rendering images and animations. For instance, to find the distance between two points in a 3D space, we use:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]
In medicine, square roots help in calculating dosages and interpreting medical test results. For example, the Body Mass Index (BMI) involves a square root in the calculation of the ideal body weight:
\[
\text{BMI} = \frac{\text{weight (kg)}}{\sqrt{\text{height (m)}}^2}
\]
In acoustics, square roots are used to compute sound intensity and pressure levels. Similarly, in signal processing, they help in the analysis and transformation of signals. For instance, the root mean square (RMS) value of a signal is given by:
\[
\text{RMS} = \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2}
\]
where \( x_i \) are the signal values and \( n \) is the number of samples.
Square roots are used in astronomy to calculate distances and gravitational forces. For example, to find the escape velocity of a planet, we use:
\[
v = \sqrt{\frac{2GM}{r}}
\]
where \( v \) is the escape velocity, \( G \) is the gravitational constant, \( M \) is the mass of the planet, and \( r \) is the radius from the center of the planet.
These examples illustrate the broad applications of square roots in various real-life scenarios, highlighting their importance in both theoretical and practical contexts.
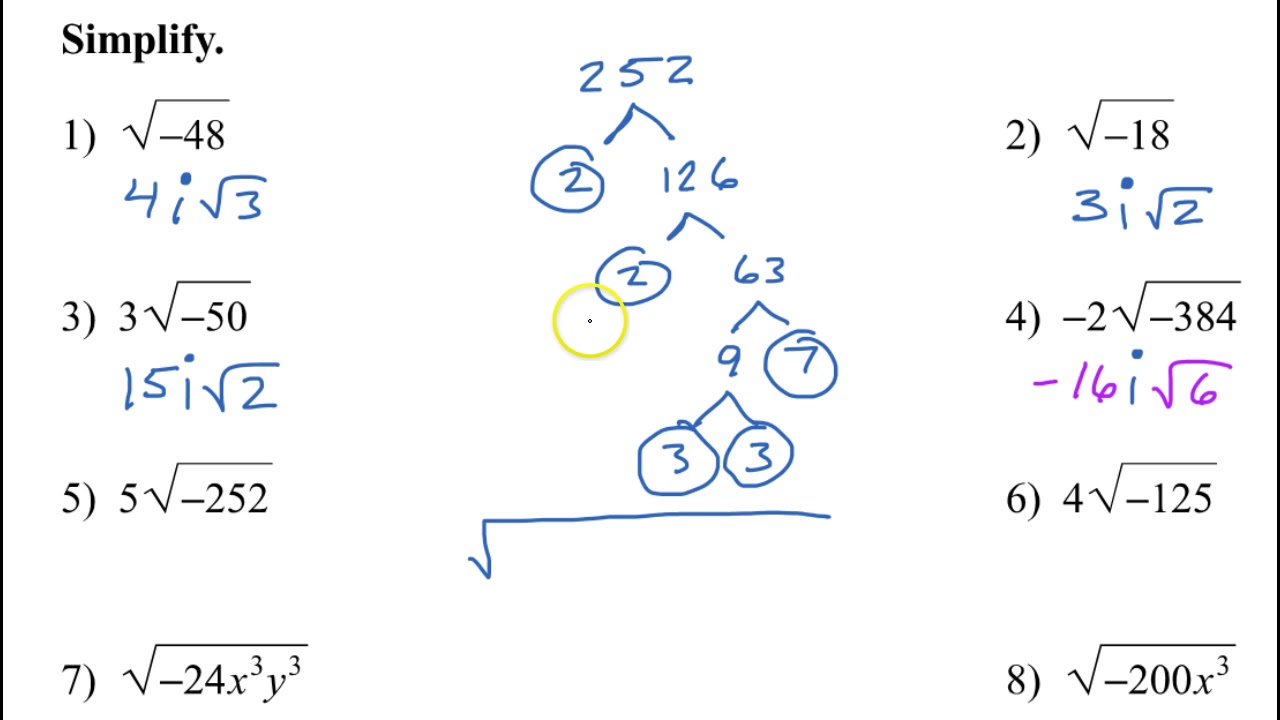
Common Mistakes to Avoid
When simplifying square roots, it’s easy to make mistakes that can lead to incorrect results. Here are some common errors to watch out for and tips on how to avoid them.
- Ignoring Prime Factorization
- Incorrectly Applying the Product Property
- Misinterpreting the Square Root of a Sum
- Overlooking Perfect Squares
- Forgetting to Simplify Completely
- Incorrectly Rationalizing the Denominator
- Confusing Different Properties of Square Roots
One of the most common mistakes is to skip the prime factorization step or to incorrectly factorize the number. Proper factorization is crucial for simplifying square roots correctly.
Tip: Break down the number completely into its prime factors before attempting to simplify.
Another frequent error is misapplying the product property, where the square root of a product is incorrectly simplified. Remember:
\[
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\]
Tip: Ensure that you only separate the square root when both \( a \) and \( b \) are positive and the product property can be applied.
Students often incorrectly simplify the square root of a sum by treating it like a product. For example, assuming \( \sqrt{a + b} = \sqrt{a} + \sqrt{b} \) is incorrect.
Tip: Understand that the square root of a sum cannot be separated into the sum of square roots.
Correct: \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\)
When simplifying, it's easy to overlook perfect squares within the radicand (the number inside the square root). This can lead to missing further simplification.
Tip: Always check if the radicand contains any perfect square factors that can be extracted.
Example: \( \sqrt{72} = \sqrt{36 \times 2} = 6 \sqrt{2} \)
Sometimes, partial simplification is done, but the expression is not fully simplified to its simplest form.
Tip: After simplifying, recheck to ensure there are no further factors or steps that can simplify the expression more.
Example: \( \sqrt{252} = \sqrt{4 \times 63} = 2 \sqrt{63} \) (not fully simplified), should be simplified to \( 6 \sqrt{7} \).
When rationalizing the denominator, students often multiply incorrectly or forget to apply the conjugate method where needed.
Tip: Use the proper technique for rationalizing, ensuring the denominator is free of square roots after simplification.
Example: To simplify \( \frac{1}{\sqrt{2}} \), multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \) to get \( \frac{\sqrt{2}}{2} \).
Mixing up the properties of square roots, such as those involving sums, differences, products, and quotients, can lead to incorrect simplifications.
Tip: Review and understand each property individually and apply them correctly in different scenarios.
By being aware of these common mistakes and taking care to avoid them, you can improve your accuracy in simplifying square roots and handling radical expressions effectively.
Practice Problems
To help you master the process of simplifying square roots, here are some practice problems along with their detailed solutions. Use these to test your understanding and improve your skills.
Problem 1
Simplify the square root of 72.
- Prime factorize 72: \(72 = 2^3 \times 3^2\).
- Group the factors into pairs: \(72 = (2 \times 2) \times (3 \times 3) \times 2\).
- Take one factor from each pair: \( \sqrt{72} = \sqrt{(2^2) \times (3^2) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
Problem 2
Simplify the square root of 200.
- Prime factorize 200: \(200 = 2^3 \times 5^2\).
- Group the factors into pairs: \(200 = (2 \times 2) \times (5 \times 5) \times 2\).
- Take one factor from each pair: \( \sqrt{200} = \sqrt{(2^2) \times (5^2) \times 2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \).
Problem 3
Simplify the square root of 98.
- Prime factorize 98: \(98 = 2 \times 7^2\).
- Group the factors into pairs: \(98 = 2 \times (7 \times 7)\).
- Take one factor from each pair: \( \sqrt{98} = \sqrt{2 \times (7^2)} = 7\sqrt{2} \).
Problem 4
Simplify the square root of 180.
- Prime factorize 180: \(180 = 2^2 \times 3^2 \times 5\).
- Group the factors into pairs: \(180 = (2 \times 2) \times (3 \times 3) \times 5\).
- Take one factor from each pair: \( \sqrt{180} = \sqrt{(2^2) \times (3^2) \times 5} = 2 \times 3 \times \sqrt{5} = 6\sqrt{5} \).
Problem 5
Simplify the square root of 252.
- Prime factorize 252: \(252 = 2^2 \times 3^2 \times 7\).
- Group the factors into pairs: \(252 = (2 \times 2) \times (3 \times 3) \times 7\).
- Take one factor from each pair: \( \sqrt{252} = \sqrt{(2^2) \times (3^2) \times 7} = 2 \times 3 \times \sqrt{7} = 6\sqrt{7} \).
Additional Practice Problems
- Simplify \( \sqrt{45} \).
- Simplify \( \sqrt{75} \).
- Simplify \( \sqrt{112} \).
- Simplify \( \sqrt{150} \).
- Simplify \( \sqrt{300} \).
Attempt these problems and use the step-by-step process to find the simplified forms.
Conclusion
Understanding and simplifying the square root of 252 demonstrates the power and beauty of mathematical principles. By breaking down the number into its prime factors and identifying perfect squares, we find that:
\[
\sqrt{252} = \sqrt{2^2 \times 3^2 \times 7} = 6\sqrt{7}
\]
This simplification shows that the square root of 252 can be expressed as \( 6\sqrt{7} \). This form is not only simpler but also provides insight into the properties of the number.
The decimal approximation of \( \sqrt{252} \approx 15.8745 \) confirms that it is an irrational number. Despite its complexity, the square root of 252 has practical applications in various fields such as geometry, physics, and engineering, where such calculations are essential.
By exploring different methods of calculating square roots, including factorization and long division, we can appreciate the versatility and depth of mathematical problem-solving. Mastery of these techniques not only aids in academic pursuits but also enhances critical thinking and analytical skills useful in real-life scenarios.
In summary, the journey to simplify the square root of 252 reveals the intricate connections within mathematics and its relevance to our everyday lives. Embrace the learning process, and continue to explore the wonders of mathematics.
Cách Đơn Giản Hóa Căn Bậc Hai của Một Số Không Phải Số Chính Phương
READ MORE:
( sqrt(63) + sqrt(252) ) * ( sqrt(175) + sqrt(28) ) = ?