3 Square Rooted: Understanding Its Importance and Applications

The square root of 3, often denoted as $$
3
, is an important mathematical constant. It is an irrational number, which means it cannot be expressed exactly as a simple fraction.

Mathematical Representation

The square root of 3 can be represented as:

Applications of the Square Root of 3

The square root of 3 appears in various mathematical contexts, including:

• Geometry: In an equilateral triangle, the height is $\frac{\sqrt{3}}{2}$ times the length of a side.
• Trigonometry: It is used in the sine and cosine of 30° and 60° angles.
• Engineering: It appears in calculations involving the three-phase electrical systems.

Approximations and Calculations

Here are a few steps to approximate the square root of 3:

1. Start with an initial guess, such as 1.5.
2. Use the Babylonian method (also known as Heron's method):
   • Take the average of the guess and the number divided by the guess.
   • Repeat the process with the new guess.
3. Continue iterating until the desired precision is achieved.

This iterative method can be represented as:

Conclusion

The square root of 3 is a fascinating number with numerous applications in mathematics, science, and engineering. Understanding its properties and methods for approximating it can be useful in various fields.

The square root of 3, denoted as √3, is an irrational number that cannot be expressed as a simple fraction. It is approximately equal to 1.73205080757. The square root of 3 arises in various mathematical, geometric, and scientific contexts, making it an important number in numerous fields.

Mathematically, the square root of 3 can be represented using the radical symbol:

\[
\sqrt{3}
\]

This value is a solution to the equation:

\[
x^2 = 3
\]

where \( x \) is the square root of 3.

The number √3 has several interesting properties and applications:

• It is an irrational number, meaning it cannot be exactly written as a fraction of two integers.
• The decimal representation of √3 is non-repeating and non-terminating.
• √3 is a crucial value in trigonometry, especially in the context of 30-60-90 triangles.

In a 30-60-90 triangle, the sides are in the ratio 1:√3:2. This makes √3 a vital component in geometric calculations involving such triangles.

Historically, the knowledge and approximation of the square root of 3 date back to ancient civilizations. It has been utilized in architectural designs, particularly in constructing equilateral triangles, where the height of the triangle is √3/2 times the side length.

Overall, understanding the square root of 3 provides insight into various mathematical concepts and their practical applications. In the subsequent sections, we will delve deeper into its mathematical definition, properties, and diverse applications.

The square root of 3, denoted as $$
3
, is a mathematical constant that represents a number which, when multiplied by itself, equals 3. It is an irrational number, which means it cannot be exactly expressed as a fraction of two integers, and its decimal representation is non-repeating and non-terminating.

The approximate value of the square root of 3 is:

$$
3 ≈ 1.7320508075688772935274463415059...

Here are some key mathematical properties and representations of the square root of 3:

• Decimal Representation: The value is approximately 1.732.
• Fractional Approximations: Some useful fractional approximations include $\frac{97}{56}$ and $\frac{265}{153}$.
• Continued Fraction: The continued fraction representation of the square root of 3 is [1; 1, 2, 1, 2, 1, 2, ...].
• Geometric Interpretation: The length of the diagonal of a unit cube (with side length 1) is $\sqrt{3}$, and it also represents the height of an equilateral triangle with side length 2.

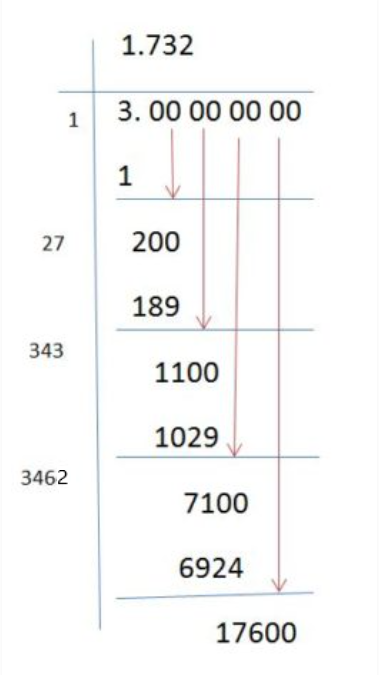
Long Division Method to Approximate the Square Root of 3

The long division method is a step-by-step approach to finding the square root of non-perfect squares. Here is a simplified outline of the process:

1. Pair the digits of the number starting from the decimal point.
2. Find the largest number whose square is less than or equal to the first pair or single digit.
3. Subtract this square from the first pair or single digit and bring down the next pair of digits.
4. Double the quotient obtained so far, and determine the next digit of the quotient by trial and error such that the product of the new quotient and the digit is less than or equal to the new dividend.
5. Repeat the process until the desired number of decimal places is obtained.

The square root of 3 calculated using this method is:

$$
3 ≈ 1.732

The square root of 3, denoted as \( \sqrt{3} \), is an important mathematical constant with various unique properties and applications in different fields. Below are some key properties:

• Irrationality:

  \( \sqrt{3} \) is an irrational number, meaning it cannot be expressed as a simple fraction of two integers. Its decimal representation is non-terminating and non-repeating, approximately equal to 1.7320508075688772...

• Algebraic Representation:

  The number can be represented in various forms, such as continued fractions. One such representation is \( \sqrt{3} = [1; 1, 2, 1, 2, \ldots] \).

• Geometric Properties:
  • The height of an equilateral triangle with side length 2 is \( \sqrt{3} \).
  • The long leg of a 30-60-90 triangle with a hypotenuse of 2 is \( \sqrt{3} \).
  • The space diagonal of a unit cube is \( \sqrt{3} \).
• Trigonometric Relationships:

  The square root of 3 appears in trigonometric functions. For example:

  • \( \tan 60^\circ = \sqrt{3} \)
  • \( \sin 60^\circ = \frac{\sqrt{3}}{2} \)
  • \( \cos 30^\circ = \frac{\sqrt{3}}{2} \)
• Engineering Applications:

  In electrical engineering, particularly in three-phase power systems, the voltage between two phases is \( \sqrt{3} \) times the line-to-neutral voltage, due to the 120-degree phase separation.

The properties of \( \sqrt{3} \) make it a crucial element in various mathematical, geometric, and engineering contexts.

The square root of 3, approximately 1.732, appears in various geometric contexts due to its unique properties. Here are some key applications:

• Equilateral Triangles: In an equilateral triangle, the height can be calculated using the formula \( h = \frac{\sqrt{3}}{2} \times a \), where \( a \) is the length of a side.
• 60-Degree Angles: The diagonal of a rhombus with 60-degree angles also involves the square root of 3.
• Hexagons: The distance between opposite sides of a regular hexagon, given side length \( a \), is \( a\sqrt{3} \).

These properties make the square root of 3 essential in fields like architecture, engineering, and various design applications.

The square root of 3, denoted as \(\sqrt{3}\), plays a significant role in trigonometry, especially in the context of special angles and their trigonometric functions.

• Tangent of 60 Degrees:

  One of the most notable appearances of \(\sqrt{3}\) is in the tangent function. The tangent of 60 degrees (\( \tan 60^\circ \)) equals \(\sqrt{3}\). This can be derived from an equilateral triangle where each angle is 60 degrees and the opposite side to the 60-degree angle in a 30-60-90 triangle is \(\sqrt{3}\).

  \[ \tan 60^\circ = \sqrt{3} \]

• Sine and Cosine of 30 and 60 Degrees:

  The sine and cosine functions for 30 degrees and 60 degrees also involve \(\sqrt{3}\). For example:

  • \(\sin 60^\circ = \frac{\sqrt{3}}{2}\)
  • \(\cos 30^\circ = \frac{\sqrt{3}}{2}\)
• Special Right Triangles:

  In a 30-60-90 triangle, the sides are in the ratio 1:\(\sqrt{3}\):2. This means that if the shortest side (opposite the 30-degree angle) is 1, the length of the side opposite the 60-degree angle is \(\sqrt{3}\), and the hypotenuse is 2.

• Trigonometric Identities:

  Several trigonometric identities and equations feature \(\sqrt{3}\). For example, the solutions to the equation \(\tan x = \sqrt{3}\) are:

  \[ x = n\pi + \frac{\pi}{3} \quad \text{or} \quad x = n\pi + \frac{2\pi}{3} \]

  where \( n \) is any integer.

Understanding these trigonometric relationships is crucial for solving various problems in mathematics and physics where these special angles frequently occur.

The square root of 3, approximately 1.732, finds extensive use in various engineering and scientific applications due to its mathematical properties.

1. Structural Engineering

In structural engineering, the square root of 3 is essential in stress and stability calculations. For example, it is used in the analysis of trusses and frames where equilateral triangles are involved. The value helps determine forces in members of the trusses under different loading conditions.

2. Electrical Engineering

Electrical engineering heavily relies on the square root of 3 in the context of three-phase power systems. The square root of 3 is used to calculate line-to-line voltages from phase voltages:

For a balanced three-phase system:

This relationship is crucial in designing and analyzing power distribution systems, ensuring efficiency and stability in power transmission.

3. Mechanical Engineering

In mechanical engineering, the square root of 3 appears in calculations related to vibrations and natural frequencies of systems. For instance, the natural frequency of an equilateral triangular plate depends on the square root of 3, influencing how the plate responds to dynamic loading.

4. Geotechnical Engineering

Geotechnical engineers use the square root of 3 in slope stability analysis. When assessing the stability of slopes and earth embankments, the factor of safety often involves calculations that include the square root of 3 to determine critical slip surfaces and potential failure planes.

5. Computer Science and Cryptography

In computer science, particularly in cryptography, the square root of 3 is part of algorithms used in secure communications and encryption methods. It helps in generating keys and ensuring the integrity and security of data transmission.

6. Physics and Material Science

Physics applications, such as calculating the properties of certain crystal structures, involve the square root of 3. In material science, it is used in determining the lattice dimensions and angles in crystalline materials, essential for understanding material properties and behaviors.

7. Finite Element Method (FEM)

The Finite Element Method, a numerical technique used for solving complex structural, fluid, and thermal problems, often employs the square root of 3 in its formulations. For example, in the analysis of stress and strain within elements, particularly triangular elements, the calculations involve the square root of 3 to accurately model and predict physical behaviors under various conditions.

Overall, the square root of 3 is a fundamental mathematical constant that facilitates various engineering and scientific calculations, contributing to advancements and efficiency in multiple fields.

There are several methods to approximate the square root of 3. Here, we will discuss three common approaches: the Babylonian method (also known as Heron's method), the binary search method, and the continued fraction method.

Babylonian Method (Heron's Method)

The Babylonian method is an iterative algorithm that converges quickly to the square root of a number. The process can be described as follows:

1. Start with an initial guess \( x_0 \). A good starting point is 1.5 for \(\sqrt{3}\).
2. Apply the iterative formula: \[ x_{n+1} = \frac{x_n + \frac{3}{x_n}}{2} \]
3. Repeat the process until the difference between \( x_{n+1} \) and \( x_n \) is less than a desired tolerance level.

For example, starting with \( x_0 = 1.5 \):

• \( x_1 = \frac{1.5 + \frac{3}{1.5}}{2} = 1.75 \)
• \( x_2 = \frac{1.75 + \frac{3}{1.75}}{2} \approx 1.732142857 \)
• Continue until desired accuracy is achieved.

Binary Search Method

The binary search method is another efficient way to approximate square roots. It works by narrowing down the interval in which the square root lies:

1. Start with an interval [a, b] where \( a = 1 \) and \( b = 2 \) because \( 1^2 < 3 < 2^2 \).
2. Compute the midpoint \( m = \frac{a + b}{2} \).
3. If \( m^2 \) is close enough to 3 (within a tolerance level), then \( m \) is the approximate square root. If not, adjust the interval:
   • If \( m^2 < 3 \), set \( a = m \).
   • If \( m^2 > 3 \), set \( b = m \).
4. Repeat steps 2 and 3 until the interval is sufficiently small.

This method converges quickly and is simple to implement.

Continued Fraction Method

Continued fractions provide another way to approximate square roots with high accuracy. The square root of 3 can be expressed as an infinite continued fraction:

Truncating the continued fraction at various points gives increasingly accurate approximations. For example:

• First approximation: \( 1 + \frac{1}{2} = 1.5 \)
• Second approximation: \( 1 + \frac{1}{2 + \frac{1}{2}} = 1.6667 \)
• Third approximation: \( 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2}}} \approx 1.7321 \)

Using a Calculator

For practical purposes, most calculators and software use advanced numerical algorithms that are variations of the methods mentioned above. For instance, the Newton-Raphson method is commonly used for its fast convergence properties.

Summary

Each method has its own advantages and can be used depending on the required precision and the available computational resources. The Babylonian method is simple and fast, binary search is robust, and continued fractions can provide highly accurate approximations with a few terms.

The discovery and understanding of square roots have ancient origins, with significant contributions from several early civilizations.

One of the earliest known records of the square root is found on a Babylonian clay tablet, dating back to between 1800 and 1600 BCE. This tablet, part of the Yale Babylonian Collection (YBC 7289), provides a method for approximating the square root of 2 and demonstrates the use of base-60 numbers to represent the value accurately to several decimal places.

In Ancient Egypt, the Rhind Mathematical Papyrus (circa 1650 BCE) showcases methods for solving quadratic equations and extracting square roots using inverse proportion techniques. These methods illustrate the Egyptians' advanced understanding of geometry and algebra.

Indian mathematicians made notable advances in the approximation of square roots. The Sulba Sutras, dated around 800-500 BCE, contain methods for finding square roots of numbers, including very accurate values for the square root of 2. Aryabhata, an Indian mathematician from the 5th century, developed techniques for calculating square roots of large numbers with impressive precision.

In Ancient Greece, the concept of irrational numbers, including the square root of non-perfect squares, was explored extensively. The mathematician Theaetetus (circa 380 BCE) is credited with proving that square roots of non-square integers are irrational. This theorem was later included in Euclid's "Elements."

The mathematical advancements of these ancient civilizations laid the groundwork for modern arithmetic and algebra, with the understanding of square roots being a fundamental component of mathematical education and application across various fields.

The square root of 3, approximately 1.732, appears in various real-world scenarios, from geometry and engineering to everyday applications. Below are some detailed examples and problems illustrating its use:

• Geometry:

  In geometry, the square root of 3 frequently appears in problems involving equilateral triangles. For instance, the height \( h \) of an equilateral triangle with side length \( a \) can be calculated using the formula \( h = \frac{\sqrt{3}}{2}a \).

  Example: Given an equilateral triangle with side length 6 units, the height can be calculated as follows:

  \[
  h = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \approx 5.196 \text{ units}
  \]

• Engineering:

  Engineers often use the square root of 3 in calculations involving power systems, especially in the context of three-phase electrical systems. The relationship between line-to-line voltage (\( V_{LL} \)) and line-to-neutral voltage (\( V_{LN} \)) in a balanced three-phase system is given by:

  \[
  V_{LL} = \sqrt{3} \times V_{LN}
  \]

  Example: If the line-to-neutral voltage of a three-phase system is 240V, the line-to-line voltage is:

  \[
  V_{LL} = \sqrt{3} \times 240V \approx 415.2V
  \]

• Construction:

  The square root of 3 is useful in construction, particularly in determining the dimensions and properties of isosceles triangles that form the basis of certain roof structures.

  Example: A roof truss forms an isosceles triangle with a base of 10 feet and a leg of 10 feet. The height of this triangle can be determined using:

  \[
  h = \sqrt{10^2 - \left(\frac{10}{2}\right)^2} = \sqrt{100 - 25} = \sqrt{75} = 5\sqrt{3} \approx 8.66 \text{ feet}
  \]

• Mathematical Problem:

  Consider a cube with a volume of 27 cubic units. The side length of the cube can be found using the cube root, which involves the square root of 3.

  Problem: Find the side length of a cube with a volume of 27 cubic units.

  Solution: The side length \( s \) is given by:

  \[
  s = \sqrt[3]{27} = 3
  \]

Understanding the square root of 3 involves addressing several common misconceptions. Clarifying these points can help improve comprehension and prevent errors in calculations.

• Misconception 1: The Square Root of a Number Has Two Values

  It is often thought that the square root of a number, such as 3, should be represented as both positive and negative values. However, the square root function \( \sqrt{x} \) is defined to produce only the non-negative value. For instance, \( \sqrt{3} \approx 1.732 \), not \(\pm 1.732\).

• Misconception 2: The Square Root Function is the Inverse of Squaring for All Real Numbers

  While it is true that squaring and taking the square root are inverse operations, this is only valid within the domain of non-negative real numbers. For example, \( \sqrt{x^2} = |x| \), which accounts for the fact that squaring a negative number also yields a positive result. Hence, \( \sqrt{(-3)^2} = \sqrt{9} = 3 \), not \(-3\).

• Misconception 3: All Square Roots are Rational Numbers

  Many assume that square roots of integers are always rational numbers. However, the square root of 3 is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal expansion is non-repeating and non-terminating.

• Misconception 4: Estimations of Square Roots are Always Accurate

  While methods such as the Babylonian method can provide close approximations of \( \sqrt{3} \), these are not exact. For precise calculations, it is important to use an appropriate number of decimal places.

• Clarification: The Square Root of Negative Numbers

  The square root of a negative number is not a real number but a complex number. For example, \( \sqrt{-3} = \sqrt{3}i \), where \( i \) is the imaginary unit.

By addressing these misconceptions, we can better understand the nature of the square root of 3 and its correct applications in mathematical contexts.

The square root of 3, denoted as \( \sqrt{3} \), has a variety of advanced theoretical applications in fields such as cryptography, navigation, and engineering. These applications leverage the mathematical properties of \( \sqrt{3} \) to solve complex problems and improve system efficiencies. Below are some detailed applications:

• Cryptography:

  In cryptography, square roots are used in algorithms for key generation and encryption. For instance, the RSA algorithm, a widely-used public-key cryptosystem, relies on the difficulty of factoring large numbers and employs modular arithmetic involving square roots to secure data. The properties of \( \sqrt{3} \) can be utilized in cryptographic protocols to enhance security.

• Navigation:

  Square roots are crucial in navigation algorithms, particularly in calculating distances and optimizing routes. In SINS/DVL (Strapdown Inertial Navigation System/Doppler Velocity Log) integrated navigation, the square-root unscented information filter (SR-UIF) improves the accuracy and stability of navigation systems by transforming the covariance matrix to ensure its positive definiteness, enhancing performance in marine and aerospace applications.

• Engineering and Signal Processing:

  In electrical engineering and signal processing, square roots are used in the design and analysis of filters and circuits. For instance, the calculation of RMS (root mean square) values for voltage and current in AC circuits involves square roots. Additionally, advanced filtering techniques, such as the Kalman filter, utilize square roots to maintain numerical stability and accuracy in state estimation.

• Statistical Mechanics and Quantum Physics:

  Square roots appear in various formulas and equations in statistical mechanics and quantum physics. The Schrödinger equation, which describes how the quantum state of a physical system changes over time, often involves operators with square root terms. These applications are fundamental in understanding particle behavior at microscopic scales.

• Geometric Analysis:

  In geometry, \( \sqrt{3} \) is significant in the analysis of equilateral triangles and hexagons. The height of an equilateral triangle with side length \( a \) is \( \frac{\sqrt{3}}{2}a \). This property is used in various geometric proofs and in calculating areas and volumes of complex shapes in higher dimensions.

These examples illustrate the versatility and importance of \( \sqrt{3} \) in advanced theoretical applications. Understanding these applications provides deeper insights into both theoretical mathematics and practical problem-solving techniques in various scientific fields.

The square root of 3 is a significant mathematical constant with various important applications across different fields. This constant, approximately equal to \( \sqrt{3} \approx 1.732 \), plays a vital role in numerous mathematical, scientific, and engineering contexts.

Throughout this article, we have explored the fundamental aspects of the square root of 3, including its mathematical definition, properties, and various applications:

• Mathematical Definition and Representation: The square root of 3 is represented as \( \sqrt{3} \) and is an irrational number, meaning it cannot be exactly expressed as a simple fraction.
• Properties: It is an important constant in algebra and geometry, particularly in relation to equilateral triangles and trigonometric functions.
• Geometric Applications: The height of an equilateral triangle, the diagonal of a cube, and other geometric constructs often involve \( \sqrt{3} \).
• Trigonometric Relevance: The square root of 3 appears in trigonometric identities and calculations, especially involving angles of 30 and 60 degrees.
• Engineering and Scientific Applications: Engineers and scientists use \( \sqrt{3} \) in various calculations, including those involving forces and electrical circuits.
• Approximations: Various methods for approximating the square root of 3 have been discussed, highlighting both historical and modern techniques.
• Historical Context: The discovery and historical significance of \( \sqrt{3} \) have been covered, showing its longstanding importance in mathematics.
• Real-world Examples: Practical examples and problems have been provided to demonstrate the real-world relevance of this constant.
• Misconceptions: Common misconceptions about the square root of 3 have been clarified to ensure a proper understanding of this mathematical constant.
• Advanced Applications: We have also delved into advanced theoretical applications, showing how \( \sqrt{3} \) is used in more complex mathematical theories and problems.

In summary, the square root of 3 is an essential mathematical constant that permeates various aspects of both theoretical and applied mathematics. Its significance extends from simple geometric calculations to complex engineering problems, making it an invaluable tool for professionals and academics alike. Understanding \( \sqrt{3} \) not only enhances one's mathematical knowledge but also provides a deeper appreciation of the interconnectedness of mathematical concepts.

We hope this comprehensive exploration of the square root of 3 has been informative and engaging, providing you with a solid foundation to appreciate its importance and applications.