3 Square Root 343: Unveiling the Mystery Behind This Mathematical Concept

The cube root of a number is a value that, when multiplied by itself three times, gives the original number. Mathematically, if \( x \) is the cube root of \( y \), then \( x^3 = y \).

Calculating the Cube Root of 343

To find the cube root of 343, we can use the notation:

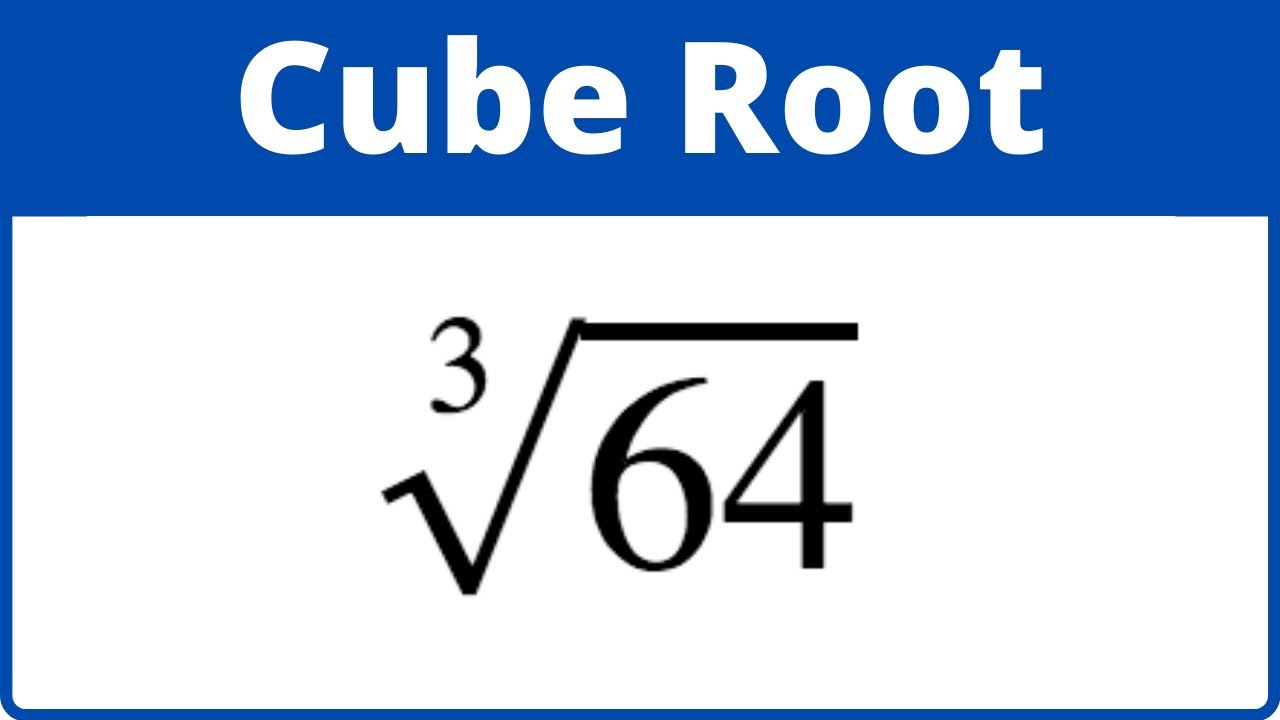
\(\sqrt[3]{343}\)

This is read as "the cube root of 343".

We need to find a number that, when raised to the power of 3, equals 343:

\( x^3 = 343 \)

Through calculation or recognition of common cubes, we find that:

\( 7 \times 7 \times 7 = 343 \)

Therefore:

\(\sqrt[3]{343} = 7\)

Verification

To verify, we can multiply 7 by itself three times:

\( 7 \times 7 = 49 \)

\( 49 \times 7 = 343 \)

Hence, our calculation is confirmed correct.

Properties of Cube Roots

• The cube root function is the inverse of the cube function.
• Every real number has exactly one real cube root.
• Cube roots can be both positive and negative. For example, the cube root of -343 is -7.

Conclusion

In conclusion, the cube root of 343 is:

\(\sqrt[3]{343} = 7\)

Understanding how to calculate and verify cube roots is a fundamental skill in mathematics that can be applied to various problems and concepts.

A cube root of a number is a special value that, when multiplied by itself three times, gives the original number. For instance, the cube root of 343 is the number that satisfies the equation \( x^3 = 343 \). This can be written as \( \sqrt[3]{343} \).

Understanding cube roots is essential in various mathematical applications, including algebra, geometry, and real-world problem solving. Here's a detailed exploration of cube roots:

• Definition: The cube root of a number \( n \) is a value \( x \) such that \( x \times x \times x = n \).
• Symbol: The cube root of \( n \) is denoted as \( \sqrt[3]{n} \).

To calculate the cube root of a number, several methods can be employed, including prime factorization, estimation, and using a calculator. Let’s explore these methods step by step using the example of finding the cube root of 343:

1. Prime Factorization Method:
   • Break down 343 into its prime factors: \( 343 = 7 \times 7 \times 7 \).
   • Since \( 343 = 7^3 \), the cube root of 343 is \( \sqrt[3]{343} = 7 \).
2. Estimation Method:
   • Find two perfect cubes between which 343 lies (for example, \( 216 = 6^3 \) and \( 512 = 8^3 \)).
   • Since 343 is closer to 512, we estimate the cube root to be closer to 7.
3. Calculator Method:
   • Use a scientific calculator to find \( \sqrt[3]{343} \).
   • Inputting 343 and pressing the cube root function will give the result of 7.

Cube roots have many applications in different fields, such as physics, engineering, and computer science. They are used to solve cubic equations, model natural phenomena, and design complex structures.

The concept of cube roots is fundamental in mathematics and involves finding a number that, when multiplied by itself three times, equals the original number. For example, the cube root of a number \( n \) is a value \( x \) such that \( x^3 = n \).

Here are the basic steps and concepts related to cube roots:

• Understanding Cube Roots:
  • The cube root of \( n \) is denoted as \( \sqrt[3]{n} \).
  • For example, \( \sqrt[3]{8} = 2 \) because \( 2 \times 2 \times 2 = 8 \).
  • Similarly, \( \sqrt[3]{27} = 3 \) because \( 3 \times 3 \times 3 = 27 \).
• Properties of Cube Roots:
  • Cube roots can be positive or negative. For instance, \( \sqrt[3]{-8} = -2 \) because \( -2 \times -2 \times -2 = -8 \).
  • Every real number has exactly one real cube root.
• Calculating Cube Roots:
  1. Prime Factorization:
     • Break down the number into its prime factors.
     • Group the prime factors into sets of three.
     • For example, \( 343 = 7 \times 7 \times 7 \). Thus, \( \sqrt[3]{343} = 7 \).
  2. Using Estimation:
     • Find two perfect cubes between which the number lies.
     • Estimate the cube root based on the proximity of the number to these cubes.
     • For instance, 343 lies between \( 216 = 6^3 \) and \( 512 = 8^3 \), so \( \sqrt[3]{343} \) is closer to 7.
  3. Using a Calculator:
     • Input the number and use the cube root function to find the value.
     • For example, input 343 and press the cube root button to get 7.

Cube roots are used in various applications, such as solving cubic equations, determining volumes, and in fields like physics and engineering. Understanding the basics of cube roots is essential for tackling more complex mathematical problems.

The cube root of a number is a value that, when multiplied by itself three times, gives the original number. Mathematically, if \( x \) is the cube root of \( n \), then \( x^3 = n \). This relationship can be expressed using the cube root symbol \( \sqrt[3]{n} \).

Here is a detailed explanation of the mathematical definition of cube roots:

• Notation and Symbols:
  • The cube root of a number \( n \) is denoted as \( \sqrt[3]{n} \).
  • For example, \( \sqrt[3]{8} = 2 \) because \( 2^3 = 8 \).
• Properties of Cube Roots:
  • Existence and Uniqueness: Every real number \( n \) has a unique real cube root.
  • Sign: The cube root of a positive number is positive, and the cube root of a negative number is negative. For instance, \( \sqrt[3]{-8} = -2 \) because \( (-2)^3 = -8 \).
• Calculating Cube Roots:
  1. Prime Factorization Method:
     • Decompose the number into its prime factors.
     • Group the prime factors into sets of three identical factors.
     • For example, \( 343 = 7 \times 7 \times 7 \), so \( \sqrt[3]{343} = 7 \).
  2. Using Estimation:
     • Identify the perfect cubes between which the number lies.
     • Estimate the cube root based on these bounds.
     • For example, 343 lies between \( 216 = 6^3 \) and \( 512 = 8^3 \), so \( \sqrt[3]{343} \) is approximately 7.
  3. Calculator Method:
     • Enter the number into a scientific calculator and use the cube root function.
     • For example, input 343 and press the cube root button to get 7.

The concept of cube roots extends beyond simple arithmetic and is used in solving cubic equations, calculating volumes, and understanding various physical phenomena. Mastery of cube roots is a crucial step in advancing mathematical knowledge and problem-solving skills.

Calculating cube roots can be done through several methods, each offering a different approach to finding the value that, when cubed, returns the original number. Here, we will explore the prime factorization method, estimation method, and calculator method in detail.

1. Prime Factorization Method:
   • Step 1: Decompose the number into its prime factors.
   • Step 2: Group the prime factors into sets of three identical factors.
   • Step 3: The cube root is the product of one factor from each group.
   • Example: To find the cube root of 343:
     1. Decompose 343 into prime factors: \( 343 = 7 \times 7 \times 7 \).
     2. Group the factors: \( (7 \times 7 \times 7) \).
     3. The cube root is 7, since \( 7^3 = 343 \).
2. Estimation Method:
   • Step 1: Identify the two perfect cubes between which the number lies.
   • Step 2: Estimate the cube root based on the proximity of the number to these perfect cubes.
   • Example: To estimate the cube root of 343:
     1. 343 lies between \( 216 = 6^3 \) and \( 512 = 8^3 \).
     2. Since 343 is closer to 216, estimate the cube root to be slightly above 6.
     3. Refine the estimate by checking values around 7. As \( 7^3 = 343 \), the cube root is 7.
3. Calculator Method:
   • Step 1: Enter the number into a scientific calculator.
   • Step 2: Use the cube root function (often labeled as \( \sqrt[3]{x} \) or with a similar notation).
   • Step 3: Read the result from the display.
   • Example: To find the cube root of 343 using a calculator:
     1. Enter 343 into the calculator.
     2. Press the cube root button to get the result of 7.

Each method offers a unique way to understand and calculate cube roots, catering to different needs and levels of precision. Mastery of these methods enables accurate and efficient solving of cubic equations and other related mathematical problems.

Calculating the cube root of a number manually involves a step-by-step process that can be understood with practice. Here, we'll demonstrate how to manually calculate the cube root of 343 using the estimation method and prime factorization method.

Estimation Method

1. Start with an initial guess. Since 343 is a perfect cube and is close to 7³, we start with an initial guess of 7.

2. Improve the estimate using the formula:

   \[
   \text{New estimate} = \frac{2 \times (\text{Current estimate}) + \frac{\text{Number}}{(\text{Current estimate})^2}}{3}
   \]

   For our example:

   \[
   \text{New estimate} = \frac{2 \times 7 + \frac{343}{7^2}}{3} = \frac{2 \times 7 + \frac{343}{49}}{3} = \frac{14 + 7}{3} = \frac{21}{3} = 7
   \]

3. Since the new estimate equals the previous estimate, we conclude that the cube root of 343 is 7.

Prime Factorization Method

1. Find the prime factorization of the number 343.

2. 343 can be divided by 7:

   \[
   343 \div 7 = 49
   \]

3. Continue dividing by 7:

   \[
   49 \div 7 = 7
   \]

4. We now have:

   \[
   343 = 7 \times 7 \times 7 = 7^3
   \]

5. Since the prime factorization of 343 is \(7^3\), the cube root of 343 is 7.

Using these methods, we have determined that the cube root of 343 is indeed 7.

The prime factorization method is a systematic way to find the cube root of a number by breaking it down into its prime factors. Let's take the number 343 as an example and find its cube root using prime factorization.

1. First, we need to factorize 343 into its prime factors. We start by dividing 343 by the smallest prime number, which is 2. Since 343 is an odd number, it is not divisible by 2.
2. Next, we try dividing 343 by the next smallest prime number, which is 3. The sum of the digits of 343 (3 + 4 + 3 = 10) is not divisible by 3, so 343 is not divisible by 3 either.
3. We then try the next prime number, which is 5. Since 343 does not end in 0 or 5, it is not divisible by 5.
4. Next, we check divisibility by 7. Dividing 343 by 7, we get 343 ÷ 7 = 49. So, 343 = 7 × 49.
5. Now we need to factorize 49. Dividing 49 by 7, we get 49 ÷ 7 = 7. Thus, 49 = 7 × 7.
6. Therefore, the prime factorization of 343 is 343 = 7 × 7 × 7 or 343 = 7³.

Since 343 is expressed as 7³, the cube root of 343 is simply the base of the exponent, which is 7.

Thus, the cube root of 343 is:

\[\sqrt[3]{343} = 7\]

Using the prime factorization method, we have determined that the cube root of 343 is 7.

The estimation method is a practical approach to finding the cube root of a number by making educated guesses and refining them. Let's use this method to estimate the cube root of 343.

1. First, identify two perfect cubes between which 343 lies. The perfect cubes around 343 are \(216\) (since \(6^3 = 216\)) and \(512\) (since \(8^3 = 512\)). Therefore, we know:

\[6^3 = 216\] \[8^3 = 512\]

2. Since \(343\) is between \(216\) and \(512\), the cube root of \(343\) must be between \(6\) and \(8\). Let's narrow it down further:
3. Try estimating with \(7\). Calculate \(7^3\) to see how close it is to \(343\):

\[7^3 = 343\]

4. Since \(7^3 = 343\), we have found that the cube root of \(343\) is exactly \(7\).

Thus, using the estimation method, we can confirm that the cube root of \(343\) is:

\[\sqrt[3]{343} = 7\]

The estimation method is useful for quickly finding the cube root of a number, especially when the number is a perfect cube or close to perfect cubes.

Calculating the cube root of a number is straightforward using a calculator. Here are the steps to find the cube root of 343 using a standard scientific calculator:

1. Turn on the calculator and ensure it is in the correct mode for root calculations. Most scientific calculators have a dedicated button for calculating cube roots, often labeled as \(\sqrt[3]{x}\) or a similar symbol.
2. Input the number 343. You can usually do this by typing the digits directly using the numeric keypad.
3. Press the cube root button (\(\sqrt[3]{x}\)). On many calculators, this button may be accessed directly or through a secondary function key (often labeled "2nd" or "Shift").
4. After pressing the cube root button, the calculator will display the result. For 343, the display should show:

\[\sqrt[3]{343} = 7\]

If your calculator does not have a dedicated cube root button, you can still find the cube root using the exponentiation function:

1. Enter the number 343.
2. Press the exponentiation button, typically labeled as \(x^y\), \(y^x\), or a similar notation.
3. Input the fraction \(\frac{1}{3}\), which represents the cube root. This can usually be done by typing "1 ÷ 3" or selecting a fraction button if available.
4. Press the equals button (=) to get the result. The display should show:

\[\sqrt[3]{343} = 7\]

Using a calculator is a quick and efficient way to find the cube root of a number, and these steps can be applied to any number where you need to find the cube root.

To understand the concept of cube roots better, let's look at the specific example of finding the cube root of 343. Here is a detailed, step-by-step process:

1. Prime Factorization Method:

   We start by factorizing 343 into its prime factors:

   • 343 is divisible by 7, giving us 343 ÷ 7 = 49.
   • 49 is also divisible by 7, giving us 49 ÷ 7 = 7.
   • Thus, 343 can be expressed as \(7 \times 7 \times 7\) or \(7^3\).

   Since \(343 = 7^3\), the cube root of 343 is \(7\).

   \[\sqrt[3]{343} = 7\]

2. Estimation Method:

   We know that:

   • \(6^3 = 216\)
   • \(8^3 = 512\)

   Since 343 is between 216 and 512, the cube root must be between 6 and 8. Testing 7, we find:

   \(7^3 = 343\), confirming that the cube root of 343 is 7.

3. Using a Calculator:
   1. Enter 343 into the calculator.
   2. Press the cube root button (\(\sqrt[3]{x}\)) or use the exponentiation function with the fraction \(\frac{1}{3}\).
   3. The calculator displays 7, confirming that the cube root of 343 is 7.

In conclusion, by using different methods such as prime factorization, estimation, and a calculator, we consistently find that the cube root of 343 is \(7\).

Calculating the cube root of a number involves several methods. Here, we will walk through a detailed step-by-step calculation to find the cube root of 343 using the prime factorization method and verification.

1. Prime Factorization Method:

   Prime factorization involves breaking down the number into its prime factors:

   • Start with the number 343.
   • Divide 343 by the smallest prime number possible. Since 343 is not even, it is not divisible by 2.
   • Check divisibility by 3. The sum of the digits of 343 (3 + 4 + 3 = 10) is not divisible by 3, so it is not divisible by 3 either.
   • Next, try 7. 343 divided by 7 gives 49, which is also divisible by 7, giving us 7. Therefore, 343 can be expressed as:

   \[343 = 7 \times 7 \times 7 = 7^3\]

   Since 343 is \(7^3\), the cube root is the base of the exponent:

   \[\sqrt[3]{343} = 7\]

2. Verification of the Result:

   To verify the cube root, we can multiply 7 by itself three times:

   \[7 \times 7 \times 7 = 343\]

   This confirms that the cube root of 343 is indeed 7.

3. Using a Calculator:

   Here are the steps to calculate the cube root of 343 using a scientific calculator:

   1. Turn on the calculator and ensure it is set to the correct mode for root calculations.
   2. Input the number 343.
   3. Press the cube root button (\(\sqrt[3]{x}\)) or use the exponentiation function with the fraction \(1/3\).
   4. The calculator should display 7, confirming that the cube root of 343 is 7.

In conclusion, by following these steps, we can consistently determine that the cube root of 343 is \(7\).

Finding the cube root of a number using the prime factorization method is a systematic approach that involves breaking down the number into its prime factors. Here is a detailed, step-by-step process to find the cube root of 343:

1. Identify the Number:

   We start with the number 343.

2. Find the Prime Factors:

   We need to determine the prime factors of 343:

   • 343 is an odd number, so it is not divisible by 2.
   • The sum of the digits (3 + 4 + 3 = 10) is not divisible by 3, so 343 is not divisible by 3.
   • 343 ends in a 3, so it is not divisible by 5.
   • Next, we try 7. Dividing 343 by 7, we get:

   \[343 \div 7 = 49\]

   • 49 is also divisible by 7, giving us:

   \[49 \div 7 = 7\]

3. Express as a Product of Prime Factors:

   From the above steps, we can express 343 as:

   \[343 = 7 \times 7 \times 7 = 7^3\]

4. Apply the Cube Root:

   To find the cube root, we take the cube root of both sides of the equation:

   \[\sqrt[3]{343} = \sqrt[3]{7^3}\]

   The cube root of \(7^3\) simplifies to 7:

   \[\sqrt[3]{343} = 7\]

5. Conclusion:

   Therefore, the cube root of 343 is:

   \[\sqrt[3]{343} = 7\]

This method confirms that 343 is a perfect cube, and its cube root is 7.

To verify the cube root of 343, we need to confirm that our calculated result, 7, when cubed, returns the original number 343. Here is a detailed verification process:

1. Initial Calculation:

   We have determined that the cube root of 343 is 7 using the prime factorization method:

   \[\sqrt[3]{343} = 7\]

2. Cubing the Result:

   To verify, we cube the result 7:

   \[7^3 = 7 \times 7 \times 7\]

   First, calculate \(7 \times 7\):

   \[7 \times 7 = 49\]

   Next, multiply 49 by 7:

   \[49 \times 7 = 343\]

3. Verification:

   Since cubing 7 returns 343, our initial calculation is verified:

   \[7^3 = 343\]

   Therefore, the cube root of 343 is indeed 7:

   \[\sqrt[3]{343} = 7\]

This verification process confirms the accuracy of our cube root calculation, demonstrating that 7 is the correct cube root of 343.

Cube roots have a variety of applications in different fields, demonstrating their practical importance beyond pure mathematics. Below are some detailed examples of how cube roots are used in real-world scenarios:

1. Geometry and Volume Calculations

Cube roots are frequently used to determine the side length of a cube given its volume. For instance, if the volume of a cube is \(343 \, \text{cm}^3\), the side length can be found using the cube root:

\[
\sqrt[3]{343 \, \text{cm}^3} = 7 \, \text{cm}
\]

2. Physics and Engineering

• Density Calculations: In physics, the density of an object can be related to its volume. When calculating the side of a cubic object to find its volume or mass, cube roots are essential.
• Material Properties: Engineering often involves using cube roots to compute properties like the radius of spheres from their volumes, which is critical in material science and mechanical engineering.

3. Real Estate and Architecture

In architecture and real estate, cube roots are used to determine the dimensions of rooms or buildings when designing spaces based on volumetric constraints. For example, if a storage container must hold a specific volume, the cube root helps in determining its optimal dimensions.

4. Environmental Science

Cube roots can be used in environmental studies to calculate properties related to natural phenomena. For example, understanding the volume of a spherical water droplet can involve using cube roots to find its radius:

\[
\text{Volume} = \frac{4}{3}\pi R^3 \implies R = \sqrt[3]{\frac{3V}{4\pi}}
\]

If the volume \(V\) is \(343\pi \, \text{cm}^3\), then:

\[
R = \sqrt[3]{\frac{3 \times 343\pi}{4\pi}} = \sqrt[3]{257.25} \approx 6.35 \, \text{cm}
\]

5. Economics and Finance

In finance, the cube root can be used in models for calculating compounded interest or in the context of cubic growth rates over time. For instance, if an investment grows to a certain volume over a period, the cube root can help determine the annual growth rate.

6. Computer Graphics and Gaming

Cube roots are used in computer graphics to manage three-dimensional modeling and animations. Calculations involving volumes and distances in 3D space often require the use of cube roots to maintain realistic proportions and scales.

7. Chemistry and Biology

• Molecular Structures: Understanding the spatial configuration of molecules involves calculations where cube roots are used to determine atomic or molecular volumes.
• Population Modeling: In biology, the growth patterns of populations that expand volumetrically can be modeled using cube roots.

8. Electrical Engineering

Cube roots are applied in electrical engineering to compute values related to power and energy. For example, in determining the optimal design and capacity of batteries and capacitors, engineers use cube roots to relate volume to capacity and other properties.

Conclusion

Cube roots are a fundamental mathematical concept with diverse applications across numerous fields, from engineering and physics to finance and environmental science. Understanding how to calculate and apply cube roots is essential for solving complex real-world problems efficiently.

Cube roots play a significant role in various real-world applications across multiple fields. Understanding and calculating cube roots can provide valuable insights and solutions in practical scenarios.

• Geometry and Volume Calculations:

  In geometry, cube roots are essential for calculating the volume of cubes and other three-dimensional shapes. For example, if you know the volume of a cube, finding the cube root helps determine the length of its edges.

• Algebra:

  Cube roots are used to solve cubic equations, which often appear in scientific and engineering problems. Solving these equations is crucial for various applications, including mechanical engineering and physics.

• Physics and Engineering:

  In physics, cube roots are involved in formulas related to density and volume. For instance, when calculating the volume of a spherical object given its mass and density, the cube root can determine the radius of the sphere.

• Pharmacology:

  Cube roots are applied in pharmacology to calculate the correct dosage of medication based on a patient's body volume. This ensures accurate and safe dosing for treatments.

• Financial Mathematics:

  In finance, cube roots are used in computing compound interest and other financial models where growth rates follow a cubic pattern. This is particularly useful for long-term investment calculations.

These applications highlight the importance of understanding cube roots, showcasing their utility beyond theoretical mathematics and into practical, real-world problem-solving.

The concept of cube roots, including the cube root of 343, has numerous applications across various fields. Here are some examples:

• Mathematics and Number Theory

  In mathematics, cube roots are essential for solving cubic equations. For example, solving \( x^3 = 343 \) directly uses the cube root, giving \( x = \sqrt[3]{343} = 7 \).

• Engineering and Architecture

  Cube roots are used in engineering to determine volumes of materials and objects. For example, if an engineer needs to design a cube-shaped container that holds a specific volume, they would use the cube root to determine the length of each side. If the volume is 343 cubic units, the side length would be \( \sqrt[3]{343} = 7 \) units.

• Physics

  In physics, cube roots can be used to calculate quantities related to three-dimensional space. For instance, the moment of inertia for a uniform cube about an axis through its center is proportional to the cube of its side length. Knowing the cube root helps simplify these calculations.

• Computer Graphics and Digital Imaging

  Cube roots are utilized in computer graphics for scaling and transformations of 3D models. When models need to be resized uniformly, the cube root helps maintain proportional scaling in all dimensions.

• Economics and Finance

  In economics, the cube root can be useful for certain financial models and growth calculations. For example, when analyzing compounded growth rates over three periods, the cube root helps determine the average growth rate per period.

• Biology and Medicine

  Cube roots can be applied in biology to study growth patterns. For example, when analyzing the growth of cells or populations in three-dimensional cultures, the cube root helps determine rates of expansion.