Topic circle perimeter and area: Discover the fundamental concepts of circle perimeter and area, key formulas for quick calculations, and their significance in everyday applications. Whether you're solving math problems or exploring geometry's real-world uses, mastering the perimeter and area of a circle is essential. Dive in to learn more about these crucial geometric properties!
Table of Content
- Circle Perimeter and Area
- Introduction to Circles
- Understanding Circle Perimeter (Circumference)
- Calculating the Circumference of a Circle
- Formulas for Circle Perimeter
- Understanding Circle Area
- Calculating the Area of a Circle
- Formulas for Circle Area
- Relationship Between Radius, Diameter, and Perimeter
- Relationship Between Radius, Diameter, and Area
- Practical Applications of Circle Perimeter and Area
- Circle Perimeter and Area in Real-World Problems
- Common Mistakes in Calculating Circle Perimeter and Area
- Advanced Topics in Circle Geometry
- FAQ on Circle Perimeter and Area
- Conclusion: Importance of Understanding Circle Geometry
- YOUTUBE:
Circle Perimeter and Area
The circle is a fundamental geometric shape defined as the set of all points in a plane that are a given distance from a given point, called the center. The distance from the center to any point on the circle is called the radius. Here, we discuss two important properties of a circle: its perimeter (also known as circumference) and its area.
Perimeter (Circumference) of a Circle
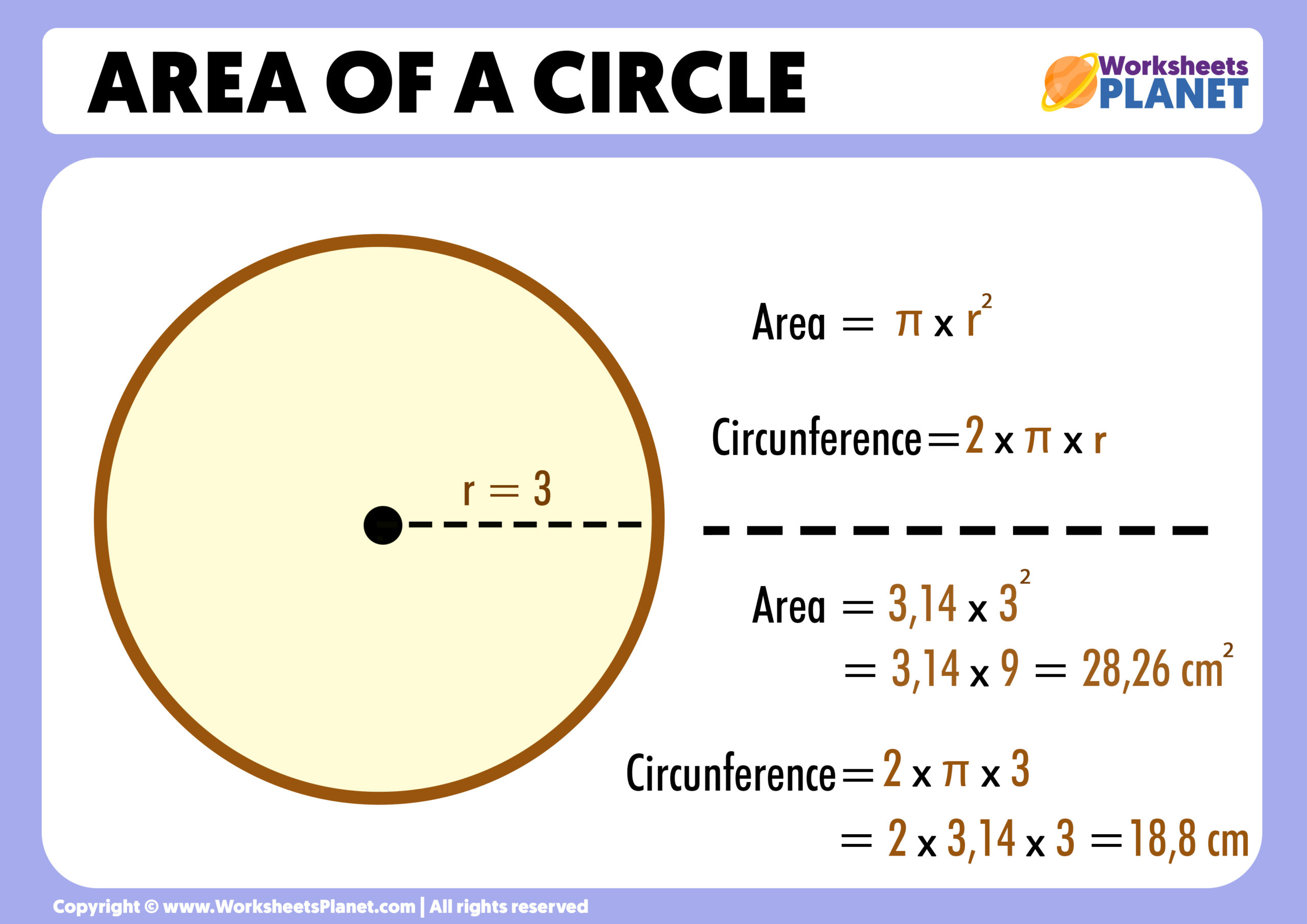
The perimeter, or circumference, of a circle is the distance around the circle. It is given by the formula:
\[ C = 2 \pi r \]
where \( C \) represents the circumference and \( r \) is the radius of the circle. Alternatively, if the diameter \( d \) (which is twice the radius) is known, the circumference can be calculated as:
\[ C = \pi d \]
Area of a Circle
The area of a circle is the region enclosed by the circle. It is calculated using the formula:
\[ A = \pi r^2 \]
where \( A \) represents the area and \( r \) is the radius. This formula shows that the area is proportional to the square of the radius.
Key Points
- The circumference (perimeter) is the linear distance around the edge of the circle.
- The area is the measure of the space enclosed within the circle.
- The constant \( \pi \) (pi) is approximately equal to 3.14159, but is often used as the symbol \( \pi \) in mathematical calculations.
- Doubling the radius of a circle quadruples the area, due to the square relationship in the area formula.
- Both the perimeter and area formulas are crucial in various applications, from engineering to everyday measurements.
Example Calculations
Consider a circle with a radius of 5 units. Using the formulas above:
- Perimeter (Circumference):
- Area:
\[
C = 2 \pi \times 5 = 10 \pi \approx 31.42 \text{ units}
\]
\[
A = \pi \times 5^2 = 25 \pi \approx 78.54 \text{ square units}
\]
Table of Circle Properties
Below is a table summarizing the formulas for the perimeter and area of a circle.
| Property | Formula |
|---|---|
| Perimeter (Circumference) | \( C = 2 \pi r \) or \( C = \pi d \) |
| Area | \( A = \pi r^2 \) |
READ MORE:
Introduction to Circles
A circle is a two-dimensional shape characterized by its perfectly round form and constant distance from its center point. Understanding circles is fundamental in geometry, as they are widely used in various applications, from design and engineering to everyday calculations. Here, we delve into the basic properties of circles and how to compute their perimeter and area.
Key properties of a circle include:
- Center: The fixed point in the middle of the circle from which all points on the circle are equidistant.
- Radius: The distance from the center of the circle to any point on the circle. Denoted as \( r \), it is a crucial measure for calculations involving circles.
- Diameter: The distance across the circle, passing through the center. It is twice the length of the radius, given by \( d = 2r \).
- Circumference: The total distance around the circle, also known as the perimeter. It can be calculated using the radius or diameter with the formula \( C = 2 \pi r \) or \( C = \pi d \).
- Area: The amount of space enclosed within the circle. It is determined by the formula \( A = \pi r^2 \), which shows how the area scales with the square of the radius.
Circles are unique in their geometric properties, and understanding these basics helps in exploring more complex topics in geometry and their practical uses. Let's explore these properties further with an example:
Consider a circle with a radius of 4 units. To find the circumference and area:
- Calculate the Circumference:
- Calculate the Area:
\[
C = 2 \pi r = 2 \pi \times 4 = 8 \pi \approx 25.12 \text{ units}
\]
\[
A = \pi r^2 = \pi \times 4^2 = 16 \pi \approx 50.27 \text{ square units}
\]
By understanding these calculations, you can apply the principles of circles to a wide range of problems, from simple geometrical tasks to complex real-world scenarios.
Understanding Circle Perimeter (Circumference)
The perimeter of a circle, commonly known as its circumference, is the total length of the boundary surrounding the circle. This concept is essential in geometry and various practical applications, such as calculating the distance around circular objects or determining the materials needed to cover or enclose a circular space.
The circumference can be understood and calculated using the following key elements:
- Radius (\( r \)): The distance from the center of the circle to any point on its edge.
- Diameter (\( d \)): The distance across the circle, passing through the center. It is twice the radius, given by the formula \( d = 2r \).
- Pi (\( \pi \)): A mathematical constant approximately equal to 3.14159. It represents the ratio of the circumference of any circle to its diameter.
The formula for calculating the circumference of a circle is derived from the relationship between the diameter and \( \pi \). The circumference \( C \) can be calculated in two ways:
- Using the radius:
\[
C = 2 \pi r
\] - Using the diameter:
\[
C = \pi d
\]
These formulas show that the circumference is directly proportional to both the radius and the diameter of the circle.
Let's look at a step-by-step example to illustrate how to calculate the circumference:
- Determine the radius: Suppose we have a circle with a radius of 7 units.
- Apply the formula using the radius:
- Alternatively, use the diameter: The diameter is twice the radius, so \( d = 14 \) units.
\[
C = \pi d = \pi \times 14 = 14 \pi \approx 43.98 \text{ units}
\]
\[
C = 2 \pi r = 2 \pi \times 7 = 14 \pi \approx 43.98 \text{ units}
\]
Understanding the circumference of a circle allows us to solve many practical problems, such as finding the length of material needed to wrap around a circular object or the distance a wheel travels after one complete revolution. Mastering these calculations is crucial for various fields, including engineering, construction, and everyday measurements.
Calculating the Circumference of a Circle
Calculating the circumference of a circle is a straightforward process once you understand the key formulas and the relationship between the circle's radius, diameter, and the constant \( \pi \). The circumference, or the perimeter of a circle, is the total distance around the circle. Here’s a step-by-step guide on how to calculate it:
To calculate the circumference, you can use either the radius or the diameter:
- Using the Radius (\( r \)):
- Using the Diameter (\( d \)):
\[
C = 2 \pi r
\]
\[
C = \pi d
\]
Both formulas are derived from the fundamental relationship involving \( \pi \), a constant that approximately equals 3.14159. Let's explore each method in detail:
- Calculate Using the Radius:
- Determine the radius (\( r \)).
- Multiply the radius by \( 2 \pi \) to get the circumference.
- Calculate Using the Diameter:
- Measure or find the diameter (\( d \)).
- Multiply the diameter by \( \pi \) to obtain the circumference.
If you know the radius of the circle, you can calculate the circumference directly. The radius is the distance from the center of the circle to any point on its boundary.
For example, for a circle with a radius of 5 units:
\[
C = 2 \pi r = 2 \pi \times 5 = 10 \pi \approx 31.42 \text{ units}
\]
This calculation shows that the circumference is approximately 31.42 units.
If you have the diameter of the circle, which is the distance across the circle passing through the center, you can use the second formula. The diameter is twice the radius.
For example, if the diameter of a circle is 10 units:
\[
C = \pi d = \pi \times 10 = 10 \pi \approx 31.42 \text{ units}
\]
Again, the circumference is approximately 31.42 units, as expected.
To summarize:
| Method | Formula | Example Calculation |
|---|---|---|
| Using Radius | \( C = 2 \pi r \) | Radius = 7 units: \[ C = 2 \pi \times 7 = 14 \pi \approx 43.98 \text{ units} \] |
| Using Diameter | \( C = \pi d \) | Diameter = 14 units: \[ C = \pi \times 14 = 14 \pi \approx 43.98 \text{ units} \] |
Understanding how to calculate the circumference of a circle is essential in many practical scenarios, such as determining the length of fencing needed to enclose a circular garden or calculating the distance a wheel travels in one complete rotation. With these formulas, you can easily find the perimeter of any circle.
Formulas for Circle Perimeter
The perimeter of a circle, also known as the circumference, is the linear distance around the edge of the circle. To calculate the perimeter, we use formulas that incorporate the circle's radius or diameter along with the mathematical constant \( \pi \). Here, we explore the key formulas for finding the circumference and how to apply them effectively.
There are two primary formulas for calculating the circumference of a circle:
- Using the Radius (\( r \)):
- Using the Diameter (\( d \)):
The radius is the distance from the center of the circle to any point on its boundary. When using the radius, the formula for the circumference \( C \) is:
\[
C = 2 \pi r
\]
Here, \( \pi \) (pi) is a constant approximately equal to 3.14159. This formula shows that the circumference is directly proportional to the radius.
The diameter is the distance across the circle through its center and is twice the length of the radius. When using the diameter, the formula for the circumference is simplified as:
\[
C = \pi d
\]
This formula indicates that the circumference is directly proportional to the diameter.
To illustrate these formulas, let’s go through detailed steps and examples:
- Calculating the Circumference Using the Radius:
- Calculating the Circumference Using the Diameter:
Suppose we have a circle with a radius of 8 units. Using the formula \( C = 2 \pi r \):
\[
C = 2 \pi \times 8 = 16 \pi \approx 50.27 \text{ units}
\]
Thus, the circumference is approximately 50.27 units.
If we have a circle with a diameter of 16 units, we apply the formula \( C = \pi d \):
\[
C = \pi \times 16 = 16 \pi \approx 50.27 \text{ units}
\]
The result is the same, as expected, confirming that both formulas are consistent.
Here’s a summary table comparing the two methods:
| Method | Formula | Example Calculation |
|---|---|---|
| Using Radius | \( C = 2 \pi r \) | Radius = 5 units: \[ C = 2 \pi \times 5 = 10 \pi \approx 31.42 \text{ units} \] |
| Using Diameter | \( C = \pi d \) | Diameter = 10 units: \[ C = \pi \times 10 = 10 \pi \approx 31.42 \text{ units} \] |
Understanding these formulas and how to apply them allows you to calculate the circumference of any circle quickly and accurately. Whether you're dealing with simple geometric problems or complex engineering tasks, these formulas provide a reliable tool for measuring the perimeter of circular shapes.

Understanding Circle Area
The area of a circle is a measure of the space enclosed within its boundary. Calculating the area is essential in various fields such as architecture, engineering, and everyday problem-solving. The area of a circle is determined using the radius, and it reveals how the space within the circle scales with changes in size.
To understand how to calculate the area of a circle, let's start with the basic formula:
\[
A = \pi r^2
\]
Here, \( A \) represents the area, \( r \) is the radius of the circle, and \( \pi \) (pi) is a constant approximately equal to 3.14159. This formula shows that the area is proportional to the square of the radius.
Let’s break down the steps to calculate the area of a circle:
- Determine the Radius:
- Apply the Formula:
The radius (\( r \)) is the distance from the center of the circle to any point on its edge. For example, if the radius is 6 units:
Substitute the radius value into the formula \( A = \pi r^2 \):
\[
A = \pi \times 6^2 = \pi \times 36 = 36 \pi \approx 113.10 \text{ square units}
\]
This calculation shows that the area of a circle with a radius of 6 units is approximately 113.10 square units.
For a clearer understanding, let’s look at another example:
- Given a Radius of 10 units:
Using the formula:
\[
A = \pi r^2 = \pi \times 10^2 = 100 \pi \approx 314.16 \text{ square units}
\]
Here, the area is approximately 314.16 square units.
In summary:
| Step | Formula | Example Calculation |
|---|---|---|
| Using Radius | \( A = \pi r^2 \) | Radius = 8 units: \[ A = \pi \times 8^2 = 64 \pi \approx 201.06 \text{ square units} \] |
Understanding how to calculate the area of a circle helps in numerous practical applications, from determining the size of a circular garden to calculating the amount of material needed to cover a round surface. This knowledge is fundamental in geometry and essential for solving a variety of real-world problems.
Calculating the Area of a Circle
Calculating the area of a circle involves determining the amount of space enclosed within its boundary. The area is a fundamental concept in geometry and is vital for various practical applications, such as estimating material requirements for circular objects or understanding spatial dimensions.
The formula for the area of a circle is based on its radius and the mathematical constant \( \pi \). The standard formula is:
\[
A = \pi r^2
\]
where \( A \) represents the area, \( r \) is the radius of the circle, and \( \pi \) (pi) is approximately 3.14159. This formula indicates that the area of a circle increases with the square of its radius.
Here’s a step-by-step guide to calculating the area of a circle:
- Identify the Radius:
- Apply the Formula:
The radius (\( r \)) is the distance from the center of the circle to any point on its edge. For instance, consider a circle with a radius of 9 units.
Insert the radius into the area formula:
\[
A = \pi r^2
\]
Using the given radius:
\[
A = \pi \times 9^2 = \pi \times 81 = 81 \pi \approx 254.47 \text{ square units}
\]
Therefore, the area of a circle with a radius of 9 units is approximately 254.47 square units.
For another example, let’s calculate the area for a circle with a different radius:
- Given a Radius of 4 units:
Using the formula:
\[
A = \pi r^2 = \pi \times 4^2 = 16 \pi \approx 50.27 \text{ square units}
\]
Here, the area is approximately 50.27 square units.
To further clarify, here’s a comparison table showing how to calculate the area for different radii:
| Radius (\( r \)) | Formula | Area (\( A \)) |
|---|---|---|
| 3 units | \( \pi r^2 \) | \[ A = \pi \times 3^2 = 9 \pi \approx 28.27 \text{ square units} \] |
| 5 units | \( \pi r^2 \) | \[ A = \pi \times 5^2 = 25 \pi \approx 78.54 \text{ square units} \] |
| 10 units | \( \pi r^2 \) | \[ A = \pi \times 10^2 = 100 \pi \approx 314.16 \text{ square units} \] |
By understanding and applying these steps, you can accurately determine the area of any circle, which is crucial for solving geometric problems and practical tasks involving circular shapes.
Formulas for Circle Area
Calculating the area of a circle involves understanding the relationship between the circle's radius, diameter, and the constant \( \pi \). The area represents the amount of space enclosed by the circle and is a fundamental concept in geometry. Below, we explore the primary formulas used to determine the area of a circle and how to apply them.
There are two main formulas for calculating the area of a circle, depending on whether you know the radius or the diameter:
- Using the Radius (\( r \)):
- Using the Diameter (\( d \)):
The radius is the distance from the center of the circle to any point on its edge. The formula for the area when the radius is known is:
\[
A = \pi r^2
\]
In this formula, \( A \) stands for the area, \( r \) is the radius, and \( \pi \) (pi) is a constant approximately equal to 3.14159.
The diameter is twice the radius, extending across the circle through its center. If you know the diameter, you can modify the radius-based formula to calculate the area as follows:
\[
A = \pi \left(\frac{d}{2}\right)^2 = \frac{\pi d^2}{4}
\]
This version of the formula allows you to calculate the area directly from the diameter.
To better understand these formulas, let’s go through detailed steps and examples for each method:
- Calculate Area Using the Radius:
- Calculate Area Using the Diameter:
Consider a circle with a radius of 7 units. Using the formula \( A = \pi r^2 \):
\[
A = \pi \times 7^2 = \pi \times 49 = 49 \pi \approx 153.94 \text{ square units}
\]
This calculation shows that the area of a circle with a radius of 7 units is approximately 153.94 square units.
If you have a circle with a diameter of 10 units, use the modified formula:
\[
A = \frac{\pi d^2}{4} = \frac{\pi \times 10^2}{4} = \frac{100 \pi}{4} = 25 \pi \approx 78.54 \text{ square units}
\]
Thus, the area of a circle with a diameter of 10 units is approximately 78.54 square units.
Here’s a comparison table summarizing these methods:
| Method | Formula | Example Calculation |
|---|---|---|
| Using Radius | \( A = \pi r^2 \) | Radius = 6 units: \[ A = \pi \times 6^2 = 36 \pi \approx 113.10 \text{ square units} \] |
| Using Diameter | \( A = \frac{\pi d^2}{4} \) | Diameter = 12 units: \[ A = \frac{\pi \times 12^2}{4} = 36 \pi \approx 113.10 \text{ square units} \] |
Understanding these formulas and their applications allows for accurate calculations of the area of a circle in various practical and theoretical scenarios. Whether you’re working with the radius or the diameter, these methods provide reliable and straightforward approaches to finding the area.
Relationship Between Radius, Diameter, and Perimeter
The perimeter of a circle, also known as the circumference, has a direct relationship with the radius and diameter of the circle. Understanding these relationships is fundamental in circle geometry. Here’s a detailed explanation:
Radius (r): The distance from the center of the circle to any point on its circumference.
Diameter (d): The distance across the circle through its center. It is twice the length of the radius.
Perimeter (Circumference, C): The total distance around the circle.
The relationships between these three properties can be summarized with the following formulas:
- Diameter and Radius:
\[ d = 2r \] - Perimeter (Circumference) and Diameter:
\[ C = \pi d \] - Perimeter (Circumference) and Radius:
\[ C = 2\pi r \]
Let's break down these relationships step by step:
- Given the radius \( r \), you can find the diameter by doubling the radius: \( d = 2r \).
- Once you have the diameter, you can calculate the circumference using the formula \( C = \pi d \).
- If you prefer to use the radius directly to find the circumference, use the formula \( C = 2\pi r \).
These relationships are visually represented in the table below:
| Property | Formula | Example (r = 5) |
|---|---|---|
| Diameter (d) | \( d = 2r \) | \( d = 2 \times 5 = 10 \) |
| Circumference (C) using Diameter | \( C = \pi d \) | \( C = \pi \times 10 \approx 31.42 \) |
| Circumference (C) using Radius | \( C = 2\pi r \) | \( C = 2 \pi \times 5 \approx 31.42 \) |
These formulas show that knowing either the radius or the diameter of a circle allows you to calculate its perimeter (circumference) easily. The constant \( \pi \) (pi) approximately equals 3.14159, which is a crucial component in these calculations.
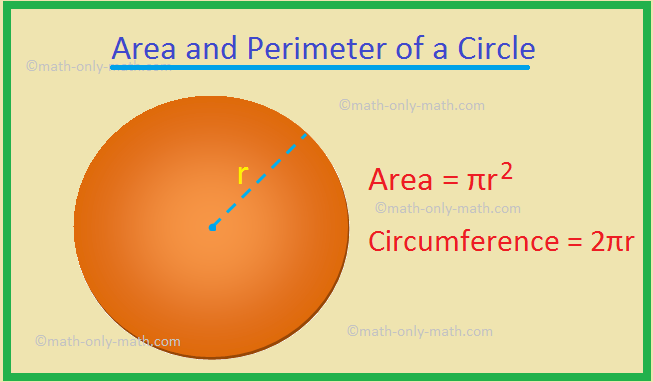
Relationship Between Radius, Diameter, and Area
The area of a circle is closely related to its radius and diameter. Understanding these relationships helps in solving various problems in circle geometry. Here’s a detailed explanation:
Radius (r): The distance from the center of the circle to any point on its circumference.
Diameter (d): The distance across the circle through its center. It is twice the length of the radius.
Area (A): The amount of space enclosed within the circle's circumference.
The relationships between these three properties can be summarized with the following formulas:
- Diameter and Radius:
\[ d = 2r \] - Area and Radius:
\[ A = \pi r^2 \] - Area and Diameter:
\[ A = \frac{\pi d^2}{4} \]
Let's break down these relationships step by step:
- Given the radius \( r \), you can find the diameter by doubling the radius: \( d = 2r \).
- Once you have the radius, you can calculate the area using the formula \( A = \pi r^2 \).
- If you prefer to use the diameter directly to find the area, use the formula \( A = \frac{\pi d^2}{4} \).
These relationships are visually represented in the table below:
| Property | Formula | Example (r = 5) |
|---|---|---|
| Diameter (d) | \( d = 2r \) | \( d = 2 \times 5 = 10 \) |
| Area (A) using Radius | \( A = \pi r^2 \) | \( A = \pi \times 5^2 \approx 78.54 \) |
| Area (A) using Diameter | \( A = \frac{\pi d^2}{4} \) | \( A = \frac{\pi \times 10^2}{4} \approx 78.54 \) |
These formulas show that knowing either the radius or the diameter of a circle allows you to calculate its area easily. The constant \( \pi \) (pi) approximately equals 3.14159, which is a crucial component in these calculations.
Practical Applications of Circle Perimeter and Area
The concepts of circle perimeter (circumference) and area are widely used in various practical applications across different fields. Understanding these applications helps in appreciating the relevance and importance of geometry in everyday life and professional fields.
1. Architecture and Construction
In architecture, the perimeter and area of circles are crucial for designing buildings, homes, and infrastructure. For example:
- Designing Circular Structures: The construction of domes, arches, and roundabouts requires precise calculations of the circle's circumference and area to ensure stability and aesthetics.
- Landscaping and Garden Design: Planning the layout of circular gardens, fountains, and pathways involves calculating the areas and perimeters to optimize space and materials.
2. Engineering
Engineering applications often involve circular shapes and require accurate perimeter and area calculations for efficiency and safety:
- Mechanical Engineering: Designing gears, wheels, and pulleys involves using the circumference to determine the distance covered in rotations.
- Civil Engineering: When constructing circular roads, tunnels, and roundabouts, engineers calculate the perimeter for proper material estimation and layout planning.
3. Art and Design
Artists and designers frequently use circles in their work, relying on geometry to achieve the desired visual effects:
- Graphic Design: Creating logos, illustrations, and patterns often involves using circles, where knowing the area helps in scaling and proportioning designs accurately.
- Fashion and Textiles: Designing circular patterns on fabrics or creating circular skirts requires calculating the fabric area to minimize waste and ensure the right fit.
4. Agriculture
In agriculture, circle geometry helps in the efficient use of space and resources:
- Crop Circles: Planning circular crop fields allows for uniform irrigation systems, maximizing the use of available water and land.
- Livestock Pens: Designing circular pens for animals helps in easier movement and better utilization of space.
5. Astronomy and Space Exploration
Understanding circular orbits and planetary motions is fundamental in astronomy:
- Planetary Orbits: Calculating the circumference of planetary orbits helps in determining the distance planets travel and their orbital periods.
- Satellite Deployment: Designing satellite trajectories involves understanding circular and elliptical orbits, using perimeter and area calculations to ensure accurate placement and functioning.
6. Everyday Applications
Circular geometry is also prevalent in daily life scenarios:
- Cooking and Baking: Measuring the circumference and area of circular baking pans ensures the correct amount of ingredients and even cooking.
- Sports and Recreation: Designing tracks, fields, and equipment like hoops and balls relies on precise calculations of perimeters and areas to meet standards and improve performance.
Conclusion
The practical applications of circle perimeter and area highlight the integral role of geometry in various aspects of life. Whether in professional fields or everyday activities, understanding these concepts enables better planning, design, and utilization of resources, enhancing efficiency and creativity.
Circle Perimeter and Area in Real-World Problems
Understanding the perimeter (circumference) and area of a circle is crucial in solving various real-world problems. Here are some practical examples:
1. Landscaping and Fencing
When planning to fence a circular garden or park, knowing the circumference helps in calculating the length of the fencing material required. For instance:
- Radius of the garden: \( r = 14 \) feet
- Circumference: \( C = 2\pi r \)
- Substitute \( \pi = \frac{22}{7} \):
- \( C = 2 \times \frac{22}{7} \times 14 = 88 \) feet
- If the cost of fencing is $20 per foot, the total cost:
- Total cost = \( 88 \times 20 = \$1760 \)
2. Painting and Flooring
When painting a circular area or installing circular flooring, the area calculation is essential. For example, painting a circular playground:
- Radius of the playground: \( r = 21 \) feet
- Area: \( A = \pi r^2 \)
- Substitute \( \pi = \frac{22}{7} \):
- \( A = \frac{22}{7} \times 21^2 = \frac{22}{7} \times 441 = 1386 \) square feet
- If one can of paint covers 100 square feet, number of cans needed:
- Number of cans = \( \frac{1386}{100} = 13.86 \approx 14 \) cans
3. Designing Circular Objects
When designing circular objects like wheels or plates, understanding their perimeter and area is crucial. For instance, finding the radius of a wheel based on its rotations and distance covered:
- Total distance covered: 10 km = 1,000,000 cm
- Number of rotations: 5000
- Circumference per rotation: \( C = \frac{1,000,000}{5000} = 200 \) cm
- Radius: \( r = \frac{200}{2\pi} = \frac{200}{2 \times \frac{22}{7}} = \frac{200 \times 7}{44} = 31.82 \) cm
4. Cost Calculation for Circular Plates
Calculating the area of circular plates to determine material costs:
- Circumference of the plate: 132 cm
- Radius: \( r = \frac{132 \times 7}{2 \times 22} = 21 \) cm
- Area: \( A = \pi r^2 = \frac{22}{7} \times 21^2 = 1386 \) square cm
5. Sports and Exercise Tracks
For circular running tracks, knowing the circumference helps in planning workouts and races. For example:
- Radius of the track: \( r = 50 \) meters
- Circumference: \( C = 2\pi r = 2 \times 3.1416 \times 50 = 314.16 \) meters
These examples illustrate the importance of understanding the perimeter and area of circles in solving practical, real-world problems efficiently.
Common Mistakes in Calculating Circle Perimeter and Area
Calculating the perimeter (circumference) and area of a circle is a fundamental skill in geometry. However, there are common mistakes that students and professionals often make. Understanding these pitfalls can help avoid errors and ensure accurate results.
Common Mistakes
-
Confusing Perimeter and Area:
One of the most frequent mistakes is confusing the formulas for the circumference (perimeter) and the area of a circle. Remember:
- Perimeter (Circumference): \( C = 2\pi r \) or \( C = \pi d \)
- Area: \( A = \pi r^2 \)
-
Incorrect Use of Pi (\(\pi\)):Pi (\(\pi\)) is an irrational number approximately equal to 3.14159. Using an incorrect value for \(\pi\) can lead to significant errors in calculations.
-
Misinterpreting the Radius and Diameter:
The radius is half the diameter of a circle. Ensure you correctly identify whether the problem provides the radius (r) or the diameter (d):
- Radius: The distance from the center to any point on the circle.
- Diameter: The distance across the circle, passing through the center, \( d = 2r \).
-
Forgetting Units:Always include the correct units in your final answer. For example, if the radius is given in centimeters, the circumference will be in centimeters, and the area will be in square centimeters.
-
Calculation Errors:
Simple arithmetic errors can lead to incorrect results. Double-check your calculations, especially when multiplying or squaring the radius.
-
Overlooking Significant Figures:
Depending on the context, it might be important to express your answer to a specific number of significant figures. Be mindful of the precision required.
Examples of Correct Calculations
Here are examples to illustrate correct calculations:
-
Given Radius:
If the radius (r) is 5 cm:
- Circumference: \( C = 2\pi r = 2\pi \times 5 \approx 31.42 \) cm
- Area: \( A = \pi r^2 = \pi \times 5^2 \approx 78.54 \) cm²
-
Given Diameter:If the diameter (d) is 10 cm:
- Circumference: \( C = \pi d = \pi \times 10 \approx 31.42 \) cm
- Area: \( A = \pi \left(\frac{d}{2}\right)^2 = \pi \left(\frac{10}{2}\right)^2 = \pi \times 5^2 \approx 78.54 \) cm²
By understanding and avoiding these common mistakes, you can ensure accurate and reliable calculations of the perimeter and area of a circle.

Advanced Topics in Circle Geometry
Circle geometry extends beyond basic properties to encompass several advanced theorems and concepts, providing deeper insights into the relationships between different geometric elements. Below are some key advanced topics in circle geometry:
1. Circle Theorems
- Angles at the Center and Circumference: The angle subtended by an arc at the center of the circle is twice the angle subtended at any point on the circumference.
- Alternate Segment Theorem: The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
- Angles in a Semicircle: Any angle inscribed in a semicircle is a right angle (90 degrees).
- Cyclic Quadrilaterals: Opposite angles of a cyclic quadrilateral sum to 180 degrees.
2. Chords and Tangents
- Equal Chords and Their Properties: Equal chords subtend equal angles at the circumference and are equidistant from the center.
- Perpendicular Tangents: A tangent to a circle forms a right angle with the radius at the point of contact.
- Power of a Point Theorem: The power of a point theorem relates the lengths of tangents and secants drawn from a point outside the circle.
3. Secant and Tangent Relationships
- Secant-Secant Theorem: If two secants intersect outside a circle, the product of the lengths of one secant segment and its external segment equals the product for the other secant.
- Secant-Tangent Theorem: If a tangent and a secant intersect outside a circle, the square of the length of the tangent is equal to the product of the lengths of the secant's external segment and its total length.
4. Coordinate Geometry of Circles
In the coordinate plane, the equation of a circle with center \((a, b)\) and radius \(r\) is given by:
\[\ (x - a)^2 + (y - b)^2 = r^2 \]
This equation is fundamental in analyzing and solving problems involving circles in coordinate geometry.
5. Applications and Proof Techniques
Advanced circle theorems are used to construct rigorous geometric proofs and solve complex problems. These theorems are applicable in various fields such as engineering, architecture, and design.
Understanding these theorems and their proofs involves:
- Identifying known properties and relevant theorems.
- Applying logical steps to demonstrate geometric facts.
- Utilizing diagrams for visual understanding and accuracy in proofs.
These advanced topics in circle geometry provide a comprehensive understanding of the intricate relationships within circles and are essential for solving higher-level geometric problems.
FAQ on Circle Perimeter and Area
Here are some frequently asked questions about the perimeter (circumference) and area of a circle:
-
Q: What is the formula for the circumference of a circle?
A: The circumference (or perimeter) of a circle is given by the formula \( C = 2\pi r \) or \( C = \pi d \), where \( r \) is the radius and \( d \) is the diameter of the circle.
-
Q: How do you calculate the area of a circle?
A: The area of a circle is calculated using the formula \( A = \pi r^2 \), where \( r \) is the radius of the circle.
-
Q: How do you find the radius if you know the circumference?
A: If you know the circumference \( C \), you can find the radius \( r \) by rearranging the circumference formula: \( r = \frac{C}{2\pi} \).
-
Q: What is the relationship between diameter and radius?
A: The diameter \( d \) of a circle is twice the radius \( r \): \( d = 2r \). Conversely, the radius is half the diameter: \( r = \frac{d}{2} \).
-
Q: How do you calculate the circumference of a semicircle?
A: The circumference of a semicircle is half the circumference of the full circle plus the diameter: \( C = \pi r + d \) or \( C = \pi r + 2r \).
-
Q: What is the formula for the area of a semicircle?
A: The area of a semicircle is half the area of the full circle: \( A = \frac{1}{2}\pi r^2 \).
-
Q: How can you find the length of an arc?
A: The length of an arc is calculated by multiplying the central angle (in radians) by the radius of the circle: \( \text{Arc Length} = \theta r \). If the angle is in degrees, use \( \text{Arc Length} = \frac{\theta}{360} \times 2\pi r \).
-
Q: Why is the unit circle important?
A: The unit circle, with a radius of 1, is crucial in trigonometry because it allows easy calculation of trigonometric functions such as sine, cosine, and tangent for any angle.
-
Q: How does the radius affect the area and circumference?
A: The area of a circle increases with the square of the radius (\( A \propto r^2 \)), while the circumference increases linearly with the radius (\( C \propto r \)).
-
Q: What are some common mistakes in calculating the perimeter and area of a circle?
A: Common mistakes include confusing the diameter with the radius, using incorrect values for π, and forgetting to square the radius when calculating the area.
Conclusion: Importance of Understanding Circle Geometry
Understanding the geometry of circles, including their perimeter (circumference) and area, is crucial for multiple reasons that extend from academic importance to practical real-world applications. Circles are fundamental geometric shapes that appear frequently in various fields, and a strong grasp of their properties can provide numerous benefits.
-
Academic Significance
In mathematics, the study of circles helps develop analytical thinking and problem-solving skills. Students learn to apply formulas such as \(C = 2\pi r\) for circumference and \(A = \pi r^2\) for area, which are essential for higher-level math and related subjects like physics and engineering.
-
Real-World Applications
- Architecture and Construction: Calculating the area and perimeter is vital in designing and constructing buildings, roads, and bridges. Precise measurements ensure structural integrity and optimal use of materials.
- Astronomy: Understanding the orbits of planets and satellites involves calculations of circular paths, where the principles of circle geometry are applied to determine distances and trajectories.
- Art and Design: Artists and designers use concepts of area and perimeter to create aesthetically pleasing and proportionate works, whether in fashion, graphic design, or spatial planning.
- Technology: In computer graphics, accurate calculations of shapes and spaces are essential for rendering images and animations, making circle geometry a key component in digital design and gaming.
-
Everyday Uses
In everyday life, understanding circle geometry can help with practical tasks such as measuring the amount of paint needed for a circular wall, designing garden layouts, or even in culinary arts where circular pans and plates are common.
Overall, the principles of circle geometry are not only academically enriching but also practically indispensable. They enhance our ability to interpret and interact with the world around us, making it a fundamental area of knowledge that everyone should strive to understand.
Math Antics - Hình tròn, Chu vi và Diện tích
Cách Tính Chu Vi Hình Tròn