Topic formula of perimeter of triangle: The formula of the perimeter of a triangle is essential for solving geometric problems and real-life applications. Learn how to calculate the perimeter for different types of triangles, from scalene to equilateral, with simple steps and examples. Master this fundamental concept and enhance your geometry skills today!
Table of Content
- Perimeter of a Triangle
- Introduction to the Perimeter of a Triangle
- Basic Formula for the Perimeter of a Triangle
- Perimeter of Different Types of Triangles
- Scalene Triangle Perimeter
- Isosceles Triangle Perimeter
- Equilateral Triangle Perimeter
- Using the Perimeter Formula in Geometry
- Perimeter Calculation Examples
- Coordinate Geometry and Triangle Perimeter
- Distance Formula Application
- Special Cases of Triangle Perimeters
- Right Triangle Perimeter
- Equilateral Triangle Perimeter Special Case
- Applications of Triangle Perimeter in Real Life
- Summary and Key Points
- Frequently Asked Questions
- YOUTUBE: Video hướng dẫn cách tìm chu vi của tam giác, phù hợp cho học sinh và người yêu thích toán học.
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its three sides. This is a fundamental concept in geometry that applies to all types of triangles, whether they are scalene, isosceles, or equilateral.
Formula
For a triangle with sides of lengths \( a \), \( b \), and \( c \), the formula for the perimeter \( P \) is:
Examples
- Scalene Triangle: A triangle with all sides of different lengths. If \( a = 5 \), \( b = 7 \), and \( c = 9 \), then \( P = 5 + 7 + 9 = 21 \).
- Isosceles Triangle: A triangle with two sides of equal length. If \( a = 6 \), \( b = 6 \), and \( c = 4 \), then \( P = 6 + 6 + 4 = 16 \).
- Equilateral Triangle: A triangle with all sides of equal length. If each side \( a = b = c = 8 \), then \( P = 8 + 8 + 8 = 24 \).
Using Variables
In a more general sense, you can use variables to represent the sides of any triangle:
Perimeter in Coordinate Geometry
If you know the coordinates of the vertices of the triangle, you can use the distance formula to find the lengths of the sides:
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
For a triangle with vertices at \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the perimeter \( P \) is:
\( P = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} + \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} + \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \)
Special Cases
- Right Triangle: For a right triangle with legs \( a \) and \( b \), and hypotenuse \( c \), the perimeter is \( P = a + b + c \).
- Equilateral Triangle: If all sides are equal (\( a = b = c \)), the perimeter simplifies to \( P = 3a \).
Understanding the formula for the perimeter of a triangle is essential for solving many problems in geometry and real-life applications. It's a straightforward calculation that helps in determining the total length around the triangle.

READ MORE:
Introduction to the Perimeter of a Triangle
The perimeter of a triangle is a fundamental concept in geometry, representing the total length around the triangle. It is calculated by summing the lengths of all three sides. Understanding this concept is crucial for solving various geometric problems and real-life applications.
The formula to calculate the perimeter \( P \) of a triangle with sides \( a \), \( b \), and \( c \) is straightforward:
\( P = a + b + c \)
Here is a step-by-step guide to understanding and calculating the perimeter of different types of triangles:
- Scalene Triangle: All three sides have different lengths. For sides \( a \), \( b \), and \( c \), the perimeter is \( P = a + b + c \).
- Isosceles Triangle: Two sides are of equal length. If the equal sides are \( a \) and the base is \( b \), the perimeter is \( P = 2a + b \).
- Equilateral Triangle: All three sides are equal. If each side is \( a \), the perimeter is \( P = 3a \).
In coordinate geometry, the perimeter can be found using the distance formula for vertices with coordinates \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\):
\( P = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} + \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} + \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \)
This comprehensive understanding of the perimeter of a triangle is essential for advancing in geometry and applying these concepts in practical situations.
Basic Formula for the Perimeter of a Triangle
The perimeter of a triangle is defined as the total length around the triangle, which is the sum of the lengths of its three sides. This basic formula is essential for solving various geometric problems and is applied universally to all triangles.
The formula to calculate the perimeter \( P \) of a triangle with sides \( a \), \( b \), and \( c \) is given by:
\( P = a + b + c \)
Here is a detailed, step-by-step explanation of how to use this formula:
- Identify the lengths of the sides: Measure or determine the lengths of the three sides of the triangle. Let's denote them as \( a \), \( b \), and \( c \).
- Apply the formula: Substitute the values of \( a \), \( b \), and \( c \) into the formula \( P = a + b + c \).
- Calculate the sum: Add the three side lengths together to find the perimeter.
For example, consider a triangle with side lengths \( a = 5 \), \( b = 7 \), and \( c = 9 \):
\( P = 5 + 7 + 9 = 21 \)
The perimeter of this triangle is 21 units.
To summarize, the basic formula for the perimeter of a triangle is simple yet powerful, allowing you to quickly determine the total length around any triangle once the side lengths are known. This concept is fundamental in geometry and has wide-ranging applications in both academic problems and real-world scenarios.
Perimeter of Different Types of Triangles
The perimeter of a triangle varies depending on the type of triangle. Each type has a specific characteristic that affects how the perimeter is calculated. Here, we will explore the perimeter formulas for scalene, isosceles, and equilateral triangles in detail.
Scalene Triangle
A scalene triangle has all sides of different lengths. The formula to calculate the perimeter of a scalene triangle is the same as the basic formula:
\( P = a + b + c \)
Where \( a \), \( b \), and \( c \) are the lengths of the three sides.
For example, if a scalene triangle has sides of lengths 6, 8, and 10 units, the perimeter is calculated as follows:
\( P = 6 + 8 + 10 = 24 \) units
Isosceles Triangle
An isosceles triangle has two sides of equal length. The formula for the perimeter of an isosceles triangle is:
\( P = 2a + b \)
Where \( a \) is the length of the two equal sides, and \( b \) is the length of the base.
For example, if an isosceles triangle has two equal sides of 5 units each and a base of 7 units, the perimeter is calculated as follows:
\( P = 2(5) + 7 = 10 + 7 = 17 \) units
Equilateral Triangle
An equilateral triangle has all three sides of equal length. The formula for the perimeter of an equilateral triangle is simplified to:
\( P = 3a \)
Where \( a \) is the length of each side.
For example, if an equilateral triangle has sides of length 9 units, the perimeter is calculated as follows:
\( P = 3(9) = 27 \) units
Understanding the perimeter formulas for different types of triangles is crucial for solving geometric problems efficiently. Each formula is derived from the basic principle of summing the side lengths, adjusted for the unique properties of each type of triangle.
Scalene Triangle Perimeter
A scalene triangle is a type of triangle where all three sides have different lengths. Calculating the perimeter of a scalene triangle involves a straightforward application of the basic perimeter formula:
\( P = a + b + c \)
Where \( a \), \( b \), and \( c \) represent the lengths of the three sides. Here is a detailed, step-by-step guide to calculating the perimeter of a scalene triangle:
- Measure or determine the lengths of the sides: Identify the lengths of all three sides of the triangle. Let's denote them as \( a \), \( b \), and \( c \).
- Apply the perimeter formula: Substitute the side lengths into the formula \( P = a + b + c \).
- Calculate the sum: Add the values of \( a \), \( b \), and \( c \) together to find the perimeter.
For example, consider a scalene triangle with side lengths \( a = 5 \) units, \( b = 7 \) units, and \( c = 9 \) units:
\( P = 5 + 7 + 9 = 21 \) units
The perimeter of this scalene triangle is 21 units.
To further illustrate, let's look at another example. If a scalene triangle has sides of lengths \( a = 6.5 \) units, \( b = 8.2 \) units, and \( c = 10.3 \) units:
\( P = 6.5 + 8.2 + 10.3 = 25 \) units
Here, the perimeter of the triangle is 25 units.
In summary, calculating the perimeter of a scalene triangle is a simple process that involves measuring the sides and adding their lengths. This method is applicable to any scalene triangle, regardless of the side lengths.

Isosceles Triangle Perimeter
An isosceles triangle is a type of triangle with two sides of equal length. Calculating the perimeter of an isosceles triangle involves summing the lengths of the two equal sides and the base. The formula for the perimeter \( P \) of an isosceles triangle is:
\( P = 2a + b \)
Where \( a \) is the length of the two equal sides, and \( b \) is the length of the base. Here is a detailed, step-by-step guide to calculating the perimeter of an isosceles triangle:
- Measure or determine the lengths of the sides: Identify the length of the two equal sides and the base. Let's denote the equal sides as \( a \) and the base as \( b \).
- Apply the perimeter formula: Substitute the side lengths into the formula \( P = 2a + b \).
- Calculate the sum: Multiply the length of the equal sides by 2, add the length of the base, and find the perimeter.
For example, consider an isosceles triangle with equal sides \( a = 6 \) units and base \( b = 8 \) units:
\( P = 2(6) + 8 = 12 + 8 = 20 \) units
The perimeter of this isosceles triangle is 20 units.
To further illustrate, let's look at another example. If an isosceles triangle has equal sides of length \( a = 5.5 \) units and a base of \( b = 7 \) units:
\( P = 2(5.5) + 7 = 11 + 7 = 18 \) units
Here, the perimeter of the triangle is 18 units.
In summary, calculating the perimeter of an isosceles triangle involves measuring the sides and applying the formula to find the total length around the triangle. This method is straightforward and applies to any isosceles triangle, regardless of the side lengths.
Equilateral Triangle Perimeter
An equilateral triangle is a type of triangle where all three sides are of equal length. Calculating the perimeter of an equilateral triangle is straightforward because of this equality. The formula for the perimeter \( P \) of an equilateral triangle is:
\( P = 3a \)
Where \( a \) is the length of each side. Here is a detailed, step-by-step guide to calculating the perimeter of an equilateral triangle:
- Measure or determine the length of one side: Since all sides are equal, you only need the length of one side. Let's denote this length as \( a \).
- Apply the perimeter formula: Substitute the length of the side into the formula \( P = 3a \).
- Calculate the product: Multiply the length of the side by 3 to find the perimeter.
For example, consider an equilateral triangle with sides of length \( a = 7 \) units:
\( P = 3(7) = 21 \) units
The perimeter of this equilateral triangle is 21 units.
To further illustrate, let's look at another example. If an equilateral triangle has sides of length \( a = 5.2 \) units:
\( P = 3(5.2) = 15.6 \) units
Here, the perimeter of the triangle is 15.6 units.
In summary, calculating the perimeter of an equilateral triangle involves measuring one side and applying the simple formula to find the total length around the triangle. This method is efficient and applies to any equilateral triangle, regardless of the side lengths.
Using the Perimeter Formula in Geometry
The perimeter of a triangle is the total length around the triangle, calculated by summing the lengths of its sides. This fundamental concept is widely used in various geometric calculations and real-world applications.
To calculate the perimeter of any triangle, you can use the following formula:
\[ \text{Perimeter} = a + b + c \]
Where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle. This formula is applicable to all types of triangles, whether they are scalene, isosceles, or equilateral.
Step-by-Step Calculation
- Measure or identify the lengths of all three sides of the triangle. For example, let the sides be \( a = 5 \, \text{cm} \), \( b = 6 \, \text{cm} \), and \( c = 7 \, \text{cm} \).
- Add the lengths together. Using the perimeter formula, sum the sides: \( 5 + 6 + 7 = 18 \, \text{cm} \).
- Express the perimeter in the appropriate unit. The result is the total perimeter of the triangle, which in this case is \( 18 \, \text{cm} \).
Example
Consider a triangle with side lengths \( a = 8 \, \text{cm} \), \( b = 10 \, \text{cm} \), and \( c = 12 \, \text{cm} \). The perimeter is calculated as follows:
\[ \text{Perimeter} = 8 \, \text{cm} + 10 \, \text{cm} + 12 \, \text{cm} = 30 \, \text{cm} \]
Using Perimeter Formula with Units
When calculating the perimeter, it’s important to ensure that all side lengths are in the same unit before performing the addition. For example, if the side lengths are given in meters, the perimeter will be in meters.
Applications in Geometry
Understanding the perimeter is crucial for solving various geometric problems. Here are some common applications:
- Determining the boundary length of a triangular plot: In landscaping and construction, knowing the perimeter helps in planning and resource allocation.
- Designing triangular objects: From triangular tables to roof trusses, knowing the perimeter is essential for material estimation.
- Solving complex geometric problems: In advanced mathematics, the perimeter of triangles often plays a role in proofs and area calculations.
Advanced Considerations
For triangles in coordinate geometry, the perimeter can be calculated using the distance formula to determine the lengths of the sides. Given the coordinates of the vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), you can calculate the side lengths as follows:
- \[ a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- \[ b = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- \[ c = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
Using these calculated side lengths, you can then find the perimeter using the initial formula.
The perimeter formula is a versatile tool in geometry, providing foundational knowledge for both simple and complex problems. Understanding and applying this formula allows for effective problem-solving and deeper exploration of geometric concepts.
Perimeter Calculation Examples
Calculating the perimeter of a triangle involves adding the lengths of its sides. Let's explore some detailed examples for different types of triangles to understand how the formula is applied in various contexts.
Example 1: Scalene Triangle
A scalene triangle has all sides of different lengths. Consider a scalene triangle with side lengths:
- \( a = 7 \, \text{cm} \)
- \( b = 9 \, \text{cm} \)
- \( c = 5 \, \text{cm} \)
To find the perimeter, sum the lengths of all sides:
\[ \text{Perimeter} = a + b + c = 7 \, \text{cm} + 9 \, \text{cm} + 5 \, \text{cm} = 21 \, \text{cm} \]
Thus, the perimeter of the triangle is \( 21 \, \text{cm} \).
Example 2: Isosceles Triangle
An isosceles triangle has two sides of equal length. Consider an isosceles triangle with:
- \( a = 10 \, \text{cm} \) (equal sides)
- \( b = 10 \, \text{cm} \) (equal sides)
- \( c = 6 \, \text{cm} \) (base)
The perimeter is calculated by summing these lengths:
\[ \text{Perimeter} = a + b + c = 10 \, \text{cm} + 10 \, \text{cm} + 6 \, \text{cm} = 26 \, \text{cm} \]
The perimeter of this isosceles triangle is \( 26 \, \text{cm} \).
Example 3: Equilateral Triangle
An equilateral triangle has all sides of equal length. If each side is:
- \( a = 8 \, \text{cm} \)
- \( b = 8 \, \text{cm} \)
- \( c = 8 \, \text{cm} \)
The perimeter can be found using the formula:
\[ \text{Perimeter} = a + b + c = 8 \, \text{cm} + 8 \, \text{cm} + 8 \, \text{cm} = 24 \, \text{cm} \]
Therefore, the perimeter of the equilateral triangle is \( 24 \, \text{cm} \).
Example 4: Right Triangle
For a right triangle, you can use the Pythagorean theorem to find the missing side if needed. Consider a right triangle with legs:
- \( a = 6 \, \text{cm} \)
- \( b = 8 \, \text{cm} \)
- \( c \) is the hypotenuse.
First, calculate the hypotenuse \( c \) using the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \, \text{cm} \]
Then, find the perimeter by summing all sides:
\[ \text{Perimeter} = a + b + c = 6 \, \text{cm} + 8 \, \text{cm} + 10 \, \text{cm} = 24 \, \text{cm} \]
Thus, the perimeter of the right triangle is \( 24 \, \text{cm} \).
Example 5: Triangle in Coordinate Geometry
Consider a triangle with vertices at coordinates \((1, 2)\), \((4, 6)\), and \((7, 2)\). Calculate the lengths of the sides using the distance formula:
- \[ a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \, \text{units} \]
- \[ b = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = 5 \, \text{units} \]
- \[ c = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{6^2 + 0^2} = 6 \, \text{units} \]
Now, sum the side lengths to find the perimeter:
\[ \text{Perimeter} = a + b + c = 5 \, \text{units} + 5 \, \text{units} + 6 \, \text{units} = 16 \, \text{units} \]
The perimeter of the triangle in the coordinate plane is \( 16 \, \text{units} \).
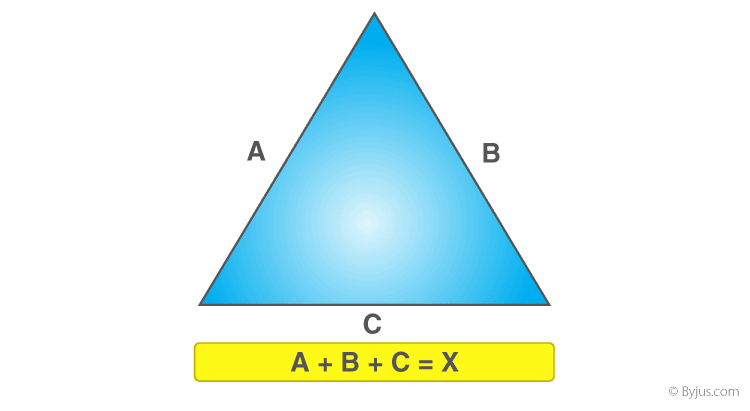
Coordinate Geometry and Triangle Perimeter
In coordinate geometry, calculating the perimeter of a triangle involves determining the distances between its vertices, which are given as coordinates in the Cartesian plane. This method is especially useful for analyzing geometric shapes in a plane and can be applied to various practical problems in mathematics and engineering.
Step-by-Step Calculation
To find the perimeter of a triangle with vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\) using coordinate geometry, follow these steps:
- Identify the coordinates of the triangle's vertices:
- Vertex \( A = (x_1, y_1) \)
- Vertex \( B = (x_2, y_2) \)
- Vertex \( C = (x_3, y_3) \)
- Calculate the distances between each pair of vertices using the distance formula:
- The distance between \( A \) and \( B \) is: \[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- The distance between \( B \) and \( C \) is: \[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- The distance between \( C \) and \( A \) is: \[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
- Add the distances to find the perimeter:
\[ \text{Perimeter} = AB + BC + CA \]
Example
Let's calculate the perimeter of a triangle with vertices at \((1, 2)\), \((4, 6)\), and \((7, 2)\).
- Calculate the distance \( AB \): \[ AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \, \text{units} \]
- Calculate the distance \( BC \): \[ BC = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = 5 \, \text{units} \]
- Calculate the distance \( CA \): \[ CA = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{6^2 + 0^2} = 6 \, \text{units} \]
- Add the distances to find the perimeter: \[ \text{Perimeter} = AB + BC + CA = 5 \, \text{units} + 5 \, \text{units} + 6 \, \text{units} = 16 \, \text{units} \]
The perimeter of the triangle is \( 16 \, \text{units} \).
Special Cases
In some cases, the vertices of the triangle may lie on the axes or form a right triangle, simplifying the calculations. For instance:
- Vertices on the same horizontal or vertical line: If two vertices have the same \( y \)-coordinate or \( x \)-coordinate, the distance calculation simplifies to the absolute difference between the coordinates.
- Right triangles: When a triangle has a right angle, you can use the Pythagorean theorem to verify the side lengths or calculate the hypotenuse, simplifying the process.
Understanding how to calculate the perimeter of a triangle in coordinate geometry allows you to solve complex problems involving geometric figures and spatial relationships efficiently.
Distance Formula Application
The distance formula is a key tool in coordinate geometry for calculating the distance between two points in the Cartesian plane. This formula is derived from the Pythagorean theorem and is essential for finding the lengths of sides of triangles, which can then be used to calculate the perimeter.
Understanding the Distance Formula
The distance formula between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
This formula calculates the straight-line distance between the two points, which corresponds to the hypotenuse of a right triangle formed by the differences in their \( x \)- and \( y \)-coordinates.
Step-by-Step Application
To apply the distance formula in the context of finding the perimeter of a triangle, follow these steps:
- Identify the coordinates of the triangle's vertices:
- Let the vertices be \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \).
- Calculate the distances between each pair of vertices:
- Distance \( AB \): \[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Distance \( BC \): \[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- Distance \( CA \): \[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
- Sum the distances to find the perimeter:
\[ \text{Perimeter} = AB + BC + CA \]
Example
Consider a triangle with vertices at \( A(2, 3) \), \( B(5, 7) \), and \( C(8, 3) \). We will calculate the perimeter using the distance formula.
- Calculate the distance \( AB \): \[ AB = \sqrt{(5 - 2)^2 + (7 - 3)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \, \text{units} \]
- Calculate the distance \( BC \): \[ BC = \sqrt{(8 - 5)^2 + (3 - 7)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = 5 \, \text{units} \]
- Calculate the distance \( CA \): \[ CA = \sqrt{(8 - 2)^2 + (3 - 3)^2} = \sqrt{6^2 + 0^2} = 6 \, \text{units} \]
- Sum the distances to find the perimeter: \[ \text{Perimeter} = AB + BC + CA = 5 \, \text{units} + 5 \, \text{units} + 6 \, \text{units} = 16 \, \text{units} \]
The perimeter of the triangle is \( 16 \, \text{units} \).
Practical Applications
The distance formula is not only used in theoretical problems but also has practical applications in various fields:
- Urban Planning and Navigation: Calculating the shortest distance between points on a map.
- Engineering: Determining the dimensions and distances in construction projects.
- Computer Graphics: Measuring distances between pixels or vertices in digital images and 3D models.
- Physics: Analyzing trajectories and paths in motion studies.
By mastering the distance formula and its application, you can effectively solve geometric problems and apply these concepts in real-world scenarios.
Special Cases of Triangle Perimeters
In certain cases, calculating the perimeter of a triangle can be simplified due to specific properties of the triangle. Below are some special cases:
Right Triangle Perimeter
A right triangle has one 90-degree angle. The sides forming the right angle are called the legs, and the side opposite the right angle is called the hypotenuse.
- The formula for the perimeter of a right triangle is:
\[ P = a + b + c \]
- Where \( a \) and \( b \) are the lengths of the legs, and \( c \) is the length of the hypotenuse. Using the Pythagorean theorem, \( c \) can be found as:
\[ c = \sqrt{a^2 + b^2} \]
Equilateral Triangle Perimeter
An equilateral triangle has all three sides of equal length.
- The formula for the perimeter of an equilateral triangle is:
\[ P = 3a \]
- Where \( a \) is the length of one side.
Isosceles Triangle Perimeter
An isosceles triangle has two sides of equal length.
- The formula for the perimeter of an isosceles triangle is:
\[ P = 2a + b \]
- Where \( a \) is the length of the two equal sides, and \( b \) is the base.
Special Formulas Involving Coordinates
When the vertices of a triangle are given in a coordinate plane, the distance formula can be used to find the lengths of the sides.
For vertices at \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the side lengths are:
- \[ a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- \[ b = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- \[ c = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
Thus, the perimeter \( P \) is:
\[ P = a + b + c \]
Special Right Triangles
Some right triangles have side lengths that follow specific ratios. These include the 45°-45°-90° and 30°-60°-90° triangles.
- For a 45°-45°-90° triangle:
If each leg has length \( a \), the hypotenuse is \( a\sqrt{2} \). The perimeter is:
\[ P = a + a + a\sqrt{2} = 2a + a\sqrt{2} \]
- For a 30°-60°-90° triangle:
If the shorter leg has length \( a \), the longer leg is \( a\sqrt{3} \), and the hypotenuse is \( 2a \). The perimeter is:
\[ P = a + a\sqrt{3} + 2a = 3a + a\sqrt{3} \]
Right Triangle Perimeter
A right triangle is a triangle in which one of the angles is exactly 90 degrees. The sides of a right triangle have special relationships defined by the Pythagorean theorem. This theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, this is represented as:
\( c^2 = a^2 + b^2 \)
Where:
- \( c \) is the length of the hypotenuse
- \( a \) and \( b \) are the lengths of the other two sides
To find the perimeter of a right triangle, you need to know the lengths of all three sides. The formula for the perimeter \( P \) is simply the sum of the lengths of these sides:
\( P = a + b + c \)
Step-by-Step Calculation
- Identify the lengths of the two legs (\( a \) and \( b \)) and the hypotenuse (\( c \)) of the right triangle.
- If only the lengths of the two legs are known, use the Pythagorean theorem to calculate the hypotenuse:
\( c = \sqrt{a^2 + b^2} \)
- Add the lengths of all three sides to find the perimeter:
\( P = a + b + c \)
Example
Consider a right triangle with legs of lengths 3 cm and 4 cm.
- Calculate the hypotenuse:
\( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{cm} \)
- Calculate the perimeter:
\( P = 3 \, \text{cm} + 4 \, \text{cm} + 5 \, \text{cm} = 12 \, \text{cm} \)
Therefore, the perimeter of this right triangle is 12 cm.
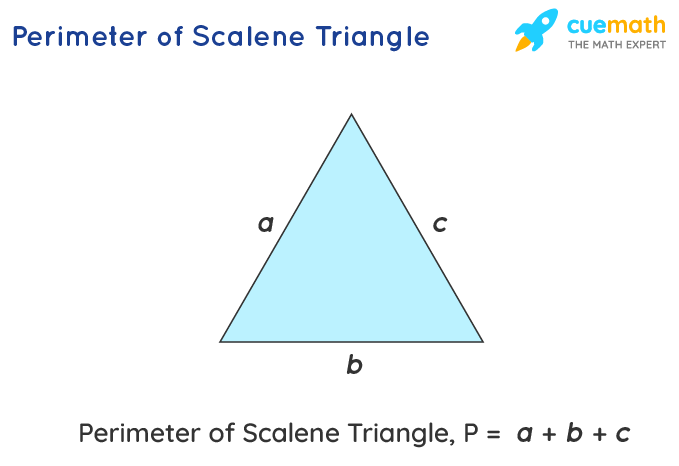
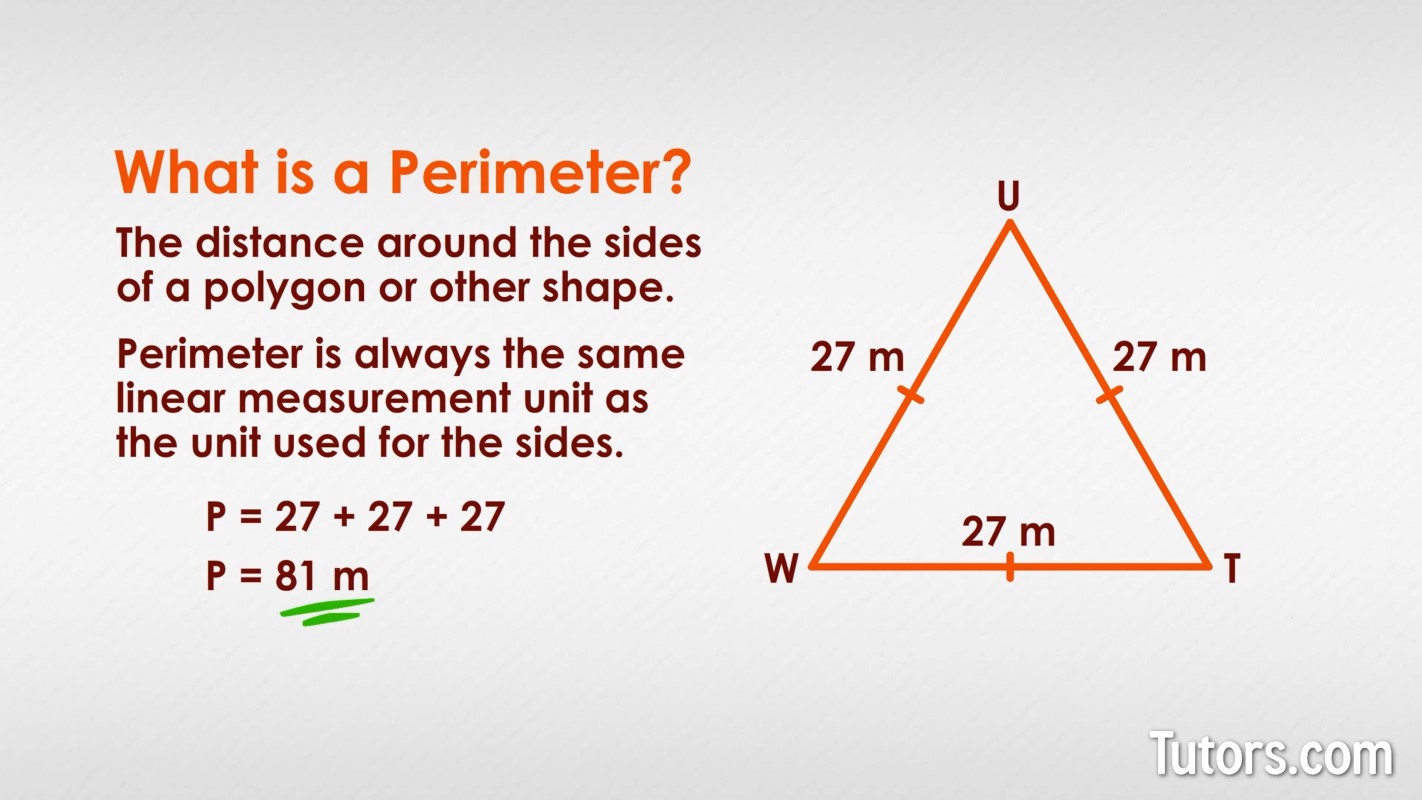
Equilateral Triangle Perimeter Special Case
An equilateral triangle is a special type of triangle where all three sides are equal in length and all three angles are equal, each measuring 60 degrees. This symmetry makes calculating the perimeter straightforward.
The formula for the perimeter \( P \) of an equilateral triangle is given by:
\[ P = 3a \]
where \( a \) is the length of each side of the equilateral triangle.
Step-by-Step Calculation
To calculate the perimeter of an equilateral triangle, follow these steps:
- Measure the length of one side of the equilateral triangle.
- Multiply this length by 3 to get the perimeter.
Examples
- Example 1: If the side length \( a \) is 5 cm, the perimeter \( P \) is: \[ P = 3 \times 5 = 15 \, \text{cm} \]
- Example 2: If the side length \( a \) is 12 units, the perimeter \( P \) is: \[ P = 3 \times 12 = 36 \, \text{units} \]
- Example 3: For a side length \( a \) of 40 inches, the perimeter \( P \) is: \[ P = 3 \times 40 = 120 \, \text{inches} \]
Additional Formulas
In addition to the perimeter, other related measurements for an equilateral triangle include:
- Semi-perimeter \( s \): \[ s = \frac{3a}{2} \]
- Height \( h \): \[ h = \frac{\sqrt{3}}{2}a \]
- Area \( A \): \[ A = \frac{\sqrt{3}}{4}a^2 \]
The properties and formulas for equilateral triangles make them useful in various geometrical calculations and real-life applications.
Applications of Triangle Perimeter in Real Life
The concept of the perimeter of a triangle is not just confined to mathematical problems; it has numerous practical applications in real life. Below are some key examples of how the perimeter of a triangle is used in various real-world scenarios:
- Construction and Architecture:
When designing buildings, architects often need to calculate the perimeter of triangular sections to determine the amount of materials needed, such as the length of beams or framing materials. For example, if a triangular gable end of a roof requires framing, knowing the perimeter helps in estimating the amount of wood or metal needed.
- Land Surveying:
Surveyors use the perimeter of triangular plots of land to determine property boundaries and calculate the total length of fencing required to enclose the property. This is particularly important in irregularly shaped parcels where traditional rectangular measurements are not applicable.
- Gardening and Landscaping:
When creating triangular flower beds or garden plots, gardeners need to calculate the perimeter to know how much border material, such as bricks or edging, is required. For instance, a triangular garden bed with sides measuring 5 meters, 7 meters, and 8 meters will have a perimeter of 20 meters, which helps in planning the layout and materials needed.
- Fencing:
For enclosing triangular areas with fencing, whether in gardens, playgrounds, or agricultural fields, the perimeter calculation is essential. This ensures that the correct length of fencing is purchased and installed.
- Crafts and Hobbies:
In various DIY projects and crafts, such as making custom picture frames or triangular decorations, knowing the perimeter is crucial. For example, if you are creating a triangular frame with sides of 10 cm, 15 cm, and 20 cm, the perimeter will be 45 cm, which helps in measuring and cutting materials accurately.
Overall, the perimeter of a triangle is a fundamental measurement that aids in efficient planning and resource management across multiple disciplines. Whether for professional use in construction and surveying or for personal projects in gardening and crafts, understanding and applying this concept is invaluable.
Summary and Key Points
Understanding the perimeter of a triangle is essential in geometry as it provides foundational knowledge for more complex mathematical concepts. Below is a comprehensive summary of the key points covered in this guide:
- Definition: The perimeter of a triangle is the total length of its boundary, calculated by summing the lengths of all three sides.
- General Formula: For any triangle with sides \(a\), \(b\), and \(c\), the perimeter \(P\) is given by: \[ P = a + b + c \]
- Special Cases:
- Equilateral Triangle: All sides are equal. If each side is \(a\), then: \[ P = 3a \]
- Isosceles Triangle: Two sides are equal. If the equal sides are \(a\) and the base is \(b\), then: \[ P = 2a + b \]
- Scalene Triangle: All sides are different. Use the general formula \(P = a + b + c\).
- Right Triangle: Includes one 90-degree angle. Using the Pythagorean theorem, the hypotenuse \(c\) can be found if the other two sides \(a\) and \(b\) are known: \[ c = \sqrt{a^2 + b^2} \] Then, the perimeter is: \[ P = a + b + c \]
- Applications: The perimeter of a triangle is used in various real-life applications such as construction, navigation, and design. It's crucial for determining the amount of materials needed for triangular structures and for solving problems in coordinate geometry.
- Coordinate Geometry: When vertices are known, distances between points can be calculated using the distance formula, and then summed to find the perimeter: \[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Examples: Practical problems involving triangles often require calculating the perimeter to find missing side lengths or to apply the triangle inequality theorem.
These key points encapsulate the essential concepts of triangle perimeters, providing a solid base for further study and practical application in various fields.
Frequently Asked Questions
-
Q1: What does the perimeter of a triangle mean?
The perimeter of a triangle is the total distance around the edges of the triangle. It is the sum of the lengths of its three sides.
-
Q2: How to calculate the perimeter of a triangle?
To calculate the perimeter of a triangle, add the lengths of its sides. If a triangle has sides \( a \), \( b \), and \( c \), the perimeter \( P \) is given by:
\[
P = a + b + c
\] -
Q3: How to find the perimeter of an equilateral triangle?
For an equilateral triangle, all three sides are equal. If each side is \( a \), the perimeter \( P \) is:
\[
P = 3a
\] -
Q4: How to find the perimeter of a right triangle?
In a right triangle, the perimeter is the sum of the lengths of the two legs and the hypotenuse. If the legs are \( a \) and \( b \), and the hypotenuse is \( c \), then:
\[
P = a + b + c
\] -
Q5: How to calculate the perimeter of a triangle given its coordinates?
First, determine the lengths of the sides using the distance formula between each pair of points. If the coordinates are \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the lengths of the sides are:
\[
a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]\[
b = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2}
\]\[
c = \sqrt{(x_1 - x_3)^2 + (y_1 - y_3)^2}
\]Then, the perimeter \( P \) is:
\[
P = a + b + c
\] -
Q6: Can a triangle have the same perimeter and area?
In some special cases, a triangle can have the same perimeter and area. Such triangles are called equable triangles.
Video hướng dẫn cách tìm chu vi của tam giác, phù hợp cho học sinh và người yêu thích toán học.
Cách Tìm Chu Vi của Tam Giác | Toán học với Thầy J
READ MORE:
Video hướng dẫn cách tìm chu vi của tam giác, giải thích công thức và cách áp dụng nó vào các bài toán thực tế.
Cách Tìm Chu Vi của Tam Giác