Topic how to find the area and perimeter of a triangle: Discover simple and effective methods to calculate the area and perimeter of any triangle. This guide provides essential formulas, step-by-step instructions, and practical examples to help you master these geometric calculations. Whether you are a student, teacher, or enthusiast, this comprehensive resource will enhance your understanding and skills.
Table of Content
- How to Find the Area and Perimeter of a Triangle
- Introduction
- Basic Definitions and Properties of Triangles
- Formulas for Area of a Triangle
- Formulas for Perimeter of a Triangle
- Step-by-Step Methods to Calculate Area and Perimeter
- Examples and Practice Problems
- Common Mistakes and How to Avoid Them
- Applications in Real Life
- Conclusion
- YOUTUBE: Hướng dẫn cách tìm diện tích và chu vi của tam giác một cách dễ hiểu và chi tiết cùng Thầy J. Phù hợp cho học sinh và người yêu thích toán học.
How to Find the Area and Perimeter of a Triangle
Understanding how to find the area and perimeter of a triangle is essential in geometry. This guide will explain the methods used for different types of triangles.
Area of a Triangle
The area of a triangle can be calculated using several formulas, depending on the known elements.
Using Base and Height
The most common method to find the area is:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Using Heron's Formula
For a triangle with sides \(a\), \(b\), and \(c\), Heron's formula can be used:
\[ s = \frac{a + b + c}{2} \]
\[ \text{Area} = \sqrt{s \cdot (s - a) \cdot (s - b) \cdot (s - c)} \]
Using Trigonometry
If two sides and the included angle are known, the area can be found using trigonometry:
\[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \]
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its sides.
\[ \text{Perimeter} = a + b + c \]
Steps to Find the Perimeter
- Measure the lengths of all three sides of the triangle.
- Add these lengths together to get the perimeter.
Examples
Example 1: Right Triangle
Given a right triangle with base \(b = 3\) units and height \(h = 4\) units:
Area:
\[ \text{Area} = \frac{1}{2} \times 3 \times 4 = 6 \text{ square units} \]
Perimeter:
\[ a = 3, b = 4, \text{ and } c = \sqrt{3^2 + 4^2} = 5 \]
\[ \text{Perimeter} = 3 + 4 + 5 = 12 \text{ units} \]
Example 2: Scalene Triangle
Given a scalene triangle with sides \(a = 5\) units, \(b = 6\) units, and \(c = 7\) units:
Area using Heron's formula:
\[ s = \frac{5 + 6 + 7}{2} = 9 \]
\[ \text{Area} = \sqrt{9 \cdot (9 - 5) \cdot (9 - 6) \cdot (9 - 7)} = \sqrt{9 \cdot 4 \cdot 3 \cdot 2} = \sqrt{216} \approx 14.7 \text{ square units} \]
Perimeter:
\[ \text{Perimeter} = 5 + 6 + 7 = 18 \text{ units} \]

READ MORE:
Introduction
Calculating the area and perimeter of a triangle is fundamental in geometry. This guide will explore various methods and formulas for finding these measurements. We'll cover:
- The definition and properties of different types of triangles
- Formulas for calculating the area using base and height, Heron's formula, trigonometry, and the shoelace theorem
- Methods to determine the perimeter for different types of triangles
- Step-by-step instructions for solving problems involving right, scalene, equilateral, and isosceles triangles
- Examples and practice problems to reinforce understanding
- Common mistakes and tips to avoid them
- Applications of these concepts in real-life scenarios
This comprehensive guide aims to enhance your understanding and skills in calculating the area and perimeter of triangles, making the process straightforward and accessible.
Basic Definitions and Properties of Triangles
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry and has several properties that are unique to it.
- Vertices: The points where the sides of a triangle meet are called vertices.
- Sides: The three straight line segments that form the triangle are called sides.
- Angles: The space between two intersecting sides is called an angle. The sum of the interior angles of a triangle is always 180 degrees.
Triangles can be classified based on the length of their sides and the measure of their angles.
Classification by Sides
- Equilateral Triangle: All three sides are of equal length, and all three interior angles are 60 degrees.
- Isosceles Triangle: Two sides have equal length, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides and all three angles are different.
Classification by Angles
- Acute Triangle: All three interior angles are less than 90 degrees.
- Right Triangle: One of the angles is exactly 90 degrees. The side opposite this angle is called the hypotenuse.
- Obtuse Triangle: One of the angles is greater than 90 degrees.
Properties of Triangles
- Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides: \( a^2 + b^2 = c^2 \).
- Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Area: The area of a triangle can be calculated using different formulas based on the known parameters:
- Base and Height: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Heron's Formula: If all three sides are known, the area can be calculated as: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \) where \( s = \frac{a + b + c}{2} \) is the semi-perimeter.
- Trigonometry: If two sides and the included angle are known, the area can be calculated as: \( \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \).
- Perimeter: The perimeter of a triangle is the sum of the lengths of its sides: \( \text{Perimeter} = a + b + c \).
Formulas for Area of a Triangle
To find the area of a triangle, different formulas can be used depending on the known parameters. Here are several methods:
Using Base and Height
The most common formula for the area of a triangle is using its base and height:
$$ A = \frac{1}{2} \times \text{base} \times \text{height} $$
This formula applies to any triangle where the base and height are known. The base is one side of the triangle, and the height is the perpendicular distance from that side to the opposite vertex.
Using Heron's Formula
Heron's formula is useful when the lengths of all three sides of the triangle are known. Let the sides be \(a\), \(b\), and \(c\), and let \(s\) be the semi-perimeter of the triangle:
$$ s = \frac{a + b + c}{2} $$
The area \(A\) is given by:
$$ A = \sqrt{s(s - a)(s - b)(s - c)} $$
Using Trigonometry
When two sides and the included angle are known, the area can be calculated using trigonometry:
$$ A = \frac{1}{2} \times a \times b \times \sin(C) $$
where \(a\) and \(b\) are the lengths of the sides, and \(C\) is the included angle.
Using Coordinates (Shoelace Theorem)
If the vertices of the triangle are known in a coordinate plane, the Shoelace Theorem can be used. For a triangle with vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the area is:
$$ A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_1 - y_1x_2 - y_2x_3 - y_3x_1 \right| $$
Special Cases
- Equilateral Triangle: All sides are equal. The formula for the area is:
$$ A = \frac{\sqrt{3}}{4} \times \text{side}^2 $$
- Isosceles Triangle: Two sides are equal. The area formula is:
$$ A = \frac{1}{4} \times b \times \sqrt{4a^2 - b^2} $$
where \(a\) is the length of the equal sides, and \(b\) is the base.
These formulas cover various scenarios and provide the tools needed to calculate the area of any triangle effectively.
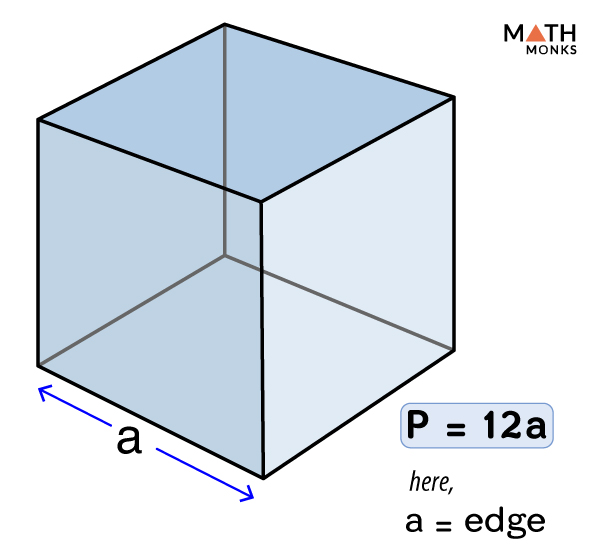
Formulas for Perimeter of a Triangle
The perimeter of a triangle is the total distance around the triangle, which can be calculated by summing the lengths of all its sides. Below are different formulas for calculating the perimeter of various types of triangles.
Sum of All Sides
For any triangle, if you know the lengths of all three sides, the perimeter \( P \) can be calculated using the formula:
\[ P = a + b + c \]
where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
Special Cases
- Equilateral Triangle: An equilateral triangle has all three sides equal. If each side has length \( s \), the perimeter \( P \) is given by:
\[ P = 3s \] - Isosceles Triangle: An isosceles triangle has two sides of equal length. If \( l \) is the length of the two equal sides and \( b \) is the length of the base, the perimeter \( P \) is given by:
\[ P = 2l + b \] - Right Triangle: A right triangle has one 90-degree angle. If the lengths of the legs are \( a \) and \( b \), and the hypotenuse is \( c \), the perimeter \( P \) is given by:
\[ P = a + b + c \]In cases where only the lengths of the legs are known, the hypotenuse can be found using the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
Using Trigonometry
In cases where the sides and angles are known, trigonometric formulas can be used to find the perimeter:
- SAS (Side-Angle-Side): If two sides and the included angle are known, the third side can be found using the law of cosines:
\[ c = \sqrt{a^2 + b^2 - 2ab \cos(\gamma)} \]Then the perimeter \( P \) is:
\[ P = a + b + c \] - ASA (Angle-Side-Angle): If two angles and the included side are known, the other sides can be found using the law of sines:
\[ \frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)} \]Then the perimeter \( P \) is:
\[ P = a + b + c \]
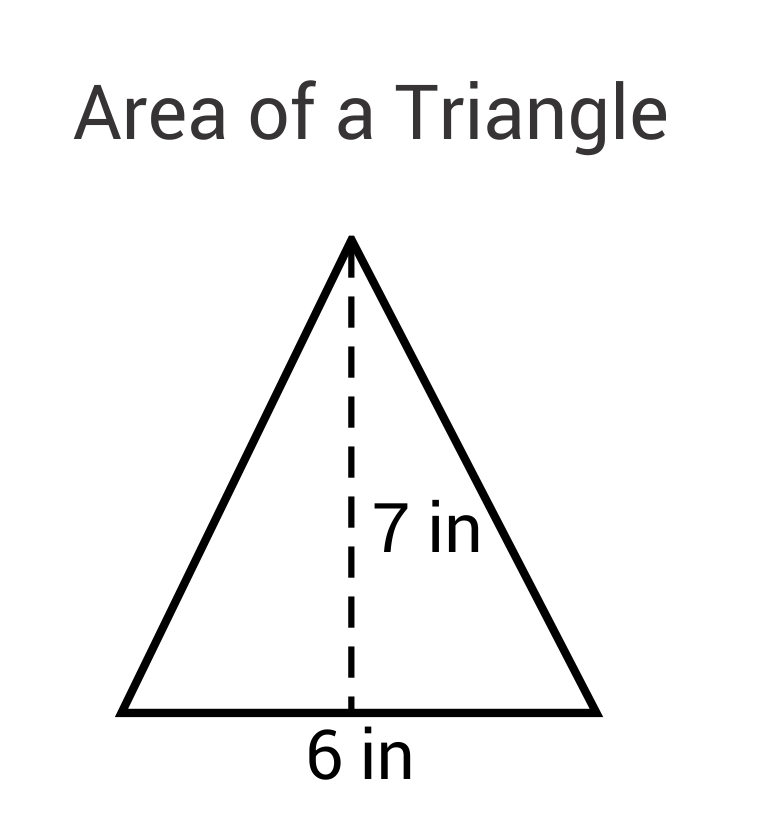
Step-by-Step Methods to Calculate Area and Perimeter
Right Triangle
To calculate the area and perimeter of a right triangle:
- Area: Use the formula \( A = \frac{1}{2} \times \text{base} \times \text{height} \).
- Identify the base (b) and the height (h), which are the two legs of the right triangle.
- Example: For a right triangle with a base of 3 cm and height of 4 cm:
\( A = \frac{1}{2} \times 3 \, \text{cm} \times 4 \, \text{cm} = 6 \, \text{cm}^2 \)
- Perimeter: Use the formula \( P = a + b + c \), where \( c \) is the hypotenuse.
- Find the hypotenuse using the Pythagorean theorem \( c = \sqrt{a^2 + b^2} \).
- Example: For a triangle with legs of 3 cm and 4 cm:
\( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{cm} \)
\( P = 3 \, \text{cm} + 4 \, \text{cm} + 5 \, \text{cm} = 12 \, \text{cm} \)
Scalene Triangle
To calculate the area and perimeter of a scalene triangle:
- Area: Use Heron's formula:
- First, find the semi-perimeter \( s = \frac{a + b + c}{2} \).
- Then, use \( A = \sqrt{s(s - a)(s - b)(s - c)} \).
- Example: For a triangle with sides 5 cm, 6 cm, and 7 cm:
\( s = \frac{5 + 6 + 7}{2} = 9 \, \text{cm} \)
\( A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14.7 \, \text{cm}^2 \)
- Perimeter: Simply add the lengths of all sides:
\( P = a + b + c \)
Example: \( P = 5 \, \text{cm} + 6 \, \text{cm} + 7 \, \text{cm} = 18 \, \text{cm} \)
Equilateral Triangle
To calculate the area and perimeter of an equilateral triangle:
- Area: Use the formula \( A = \frac{\sqrt{3}}{4} \times a^2 \), where \( a \) is the side length.
- Example: For a triangle with a side length of 6 cm:
\( A = \frac{\sqrt{3}}{4} \times 6^2 = \frac{\sqrt{3}}{4} \times 36 = 9\sqrt{3} \approx 15.6 \, \text{cm}^2 \)
- Example: For a triangle with a side length of 6 cm:
- Perimeter: Multiply the side length by 3:
\( P = 3a \)
Example: \( P = 3 \times 6 \, \text{cm} = 18 \, \text{cm} \)
Isosceles Triangle
To calculate the area and perimeter of an isosceles triangle:
- Area: Use the formula \( A = \frac{1}{2} \times b \times h \), where \( b \) is the base and \( h \) is the height.
- Height can be found using the Pythagorean theorem if necessary.
- Example: For a triangle with base 8 cm and height 5 cm:
\( A = \frac{1}{2} \times 8 \, \text{cm} \times 5 \, \text{cm} = 20 \, \text{cm}^2 \)
- Perimeter: Add the lengths of the two equal sides and the base:
\( P = 2a + b \)
Example: For equal sides of 6 cm and a base of 8 cm:
\( P = 2 \times 6 \, \text{cm} + 8 \, \text{cm} = 20 \, \text{cm} \)
Examples and Practice Problems
Example Problems with Solutions
Let's go through a few examples to understand how to calculate the area and perimeter of different types of triangles.
Example 1: Right Triangle
Given a right-angled triangle with a base of 12 units and a height of 5 units, find its area and perimeter.
- Area:
- Perimeter:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 12 \times 5 = 30 \text{ square units}
\]
Using the Pythagorean theorem to find the hypotenuse:
\[
c = \sqrt{a^2 + b^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13
\]
So, the perimeter is:
\[
\text{Perimeter} = a + b + c = 12 + 5 + 13 = 30 \text{ units}
\]
Example 2: Equilateral Triangle
Determine the area and perimeter of an equilateral triangle with a side length of 9 units.
- Area:
- Perimeter:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2 = \frac{\sqrt{3}}{4} \times 9^2 = \frac{81\sqrt{3}}{4} \approx 35.07 \text{ square units}
\]
\[
\text{Perimeter} = 3 \times \text{side} = 3 \times 9 = 27 \text{ units}
\]
Example 3: Isosceles Triangle
Find the area and perimeter of an isosceles triangle with two equal sides of length 6 units each and a base of 8 units.
- Area:
- Perimeter:
\[
\text{Area} = \frac{1}{2} \times b \times \sqrt{a^2 - \frac{b^2}{4}} = \frac{1}{2} \times 8 \times \sqrt{6^2 - \frac{8^2}{4}} = \frac{1}{2} \times 8 \times \sqrt{36 - 16} = \frac{1}{2} \times 8 \times \sqrt{20} \approx 17.89 \text{ square units}
\]
\[
\text{Perimeter} = 2a + b = 2 \times 6 + 8 = 12 + 8 = 20 \text{ units}
\]
Practice Problems
- Calculate the area and perimeter of a scalene triangle with sides 7 units, 8 units, and 5 units.
- Find the area and perimeter of a right triangle with legs of length 9 units and 12 units.
- Determine the area of an equilateral triangle with a side length of 10 units.
- Find the perimeter of an isosceles triangle with sides of 10 units, 10 units, and 12 units.
Common Mistakes and How to Avoid Them
Calculating the area and perimeter of a triangle can sometimes be tricky. Here are some common mistakes students often make and tips on how to avoid them:
-
Mistake: Confusing the formulas for area and perimeter
It's easy to mix up the formulas. Remember, the area is calculated using \( \frac{1}{2} \times \text{base} \times \text{height} \), while the perimeter is the sum of all sides.
Solution: Always double-check which measurement you need and use the correct formula. Label your calculations clearly.
-
Mistake: Using the wrong height
For the area formula, the height must be perpendicular to the base. Students sometimes use a slanted side instead.
Solution: Identify the base and find the height that meets it at a right angle.
Example:
Correct: Height is perpendicular to the base. Incorrect: Height is along a slanted side. -
Mistake: Not converting units
When sides of a triangle are given in different units, students might forget to convert them to a common unit before calculating.
Solution: Always convert all measurements to the same unit before performing calculations.
Example: If one side is in meters and another in centimeters, convert centimeters to meters or vice versa before adding or multiplying.
-
Mistake: Adding sides incorrectly for perimeter
Some students might think the order in which sides are added matters, or they might forget a side.
Solution: Use the commutative property of addition, which means sides can be added in any order, and ensure all sides are included.
- Identify all three sides.
- Add them together.
-
Mistake: Incorrectly applying Heron's formula
Heron's formula requires the semi-perimeter and can be misapplied if steps are skipped or values are miscalculated.
Solution: Follow each step methodically:
- Calculate the semi-perimeter \( s = \frac{a + b + c}{2} \).
- Apply the formula \( \sqrt{s(s-a)(s-b)(s-c)} \).
-
Mistake: Rounding errors
Rounding intermediate results too early can lead to inaccurate final results.
Solution: Keep numbers in full precision until the final step, then round the final answer if necessary.
-
Mistake: Using the incorrect base-height pair in trigonometric methods
When using trigonometric functions, students sometimes pair the wrong base with the wrong height or angle.
Solution: Carefully identify the correct base and corresponding height or angle. Use appropriate trigonometric identities.
By recognizing these common mistakes and understanding how to avoid them, you can more accurately calculate the area and perimeter of triangles.
Applications in Real Life
The concepts of area and perimeter of a triangle are not just academic exercises; they have numerous practical applications in various fields. Understanding how to calculate these measurements can be highly beneficial in real-world scenarios. Here are some common applications:
- Architecture and Construction: When designing buildings and other structures, architects and engineers need to know the area and perimeter of triangular sections. This helps in determining the amount of materials needed and ensuring structural integrity.
- Landscaping and Gardening: Gardeners and landscapers use these calculations to design triangular flower beds or lawns. Knowing the area helps in determining the amount of soil, fertilizer, and seeds required.
- Fencing: Farmers and property owners often need to calculate the perimeter of triangular plots of land to determine the length of fencing required.
- Art and Design: Artists and designers use triangles in their work, from creating patterns to constructing geometric art pieces. Calculating the area and perimeter helps in planning and material usage.
- Navigation and Surveying: In fields like navigation and land surveying, the area and perimeter of triangular plots are crucial for accurate mapping and property delineation.
- Sports Fields: Designing sports fields, such as soccer or baseball fields, often involves calculating the area and perimeter of triangular sections for proper layout and markings.
These applications show the importance of understanding and accurately calculating the area and perimeter of triangles. By mastering these concepts, you can effectively tackle various practical problems in everyday life.

Conclusion
Understanding how to find the area and perimeter of a triangle is fundamental in geometry and has practical applications in various fields. This article has provided a comprehensive guide on different methods to calculate the area and perimeter of triangles, including using base and height, Heron's formula, trigonometry, and coordinates for the area, and summing the lengths of sides for the perimeter.
Knowing these formulas allows for solving real-life problems such as determining the amount of material needed for construction, land measurement, and even in art and design. For instance, architects use these calculations to plan the layout of buildings and structures, while engineers apply them in designing and analyzing various components.
Additionally, the practice problems and step-by-step methods provided aim to reinforce the understanding and application of these formulas. Regular practice can help avoid common mistakes and improve problem-solving skills.
In conclusion, mastering the calculations of the area and perimeter of triangles not only enhances mathematical proficiency but also equips individuals with essential tools for practical and professional tasks. Keep practicing and exploring more complex problems to further deepen your understanding and capability in geometry.
Hướng dẫn cách tìm diện tích và chu vi của tam giác một cách dễ hiểu và chi tiết cùng Thầy J. Phù hợp cho học sinh và người yêu thích toán học.
Cách Tìm Diện Tích và Chu Vi của Tam Giác | Toán Học với Thầy J
READ MORE:
Hướng dẫn chi tiết cách tìm diện tích và chu vi của tam giác một cách dễ hiểu. Phù hợp cho học sinh và người yêu thích toán học.
Cách Tìm Diện Tích và Chu Vi của Tam Giác