Topic finding perimeter of a triangle: Discover how simple it is to find the perimeter of a triangle with our easy-to-follow guide. Learn the essential formulas, steps, and special cases, including equilateral, isosceles, and scalene triangles. Enhance your understanding with practical examples and avoid common mistakes. Perfect for students, teachers, and anyone looking to master this fundamental geometry skill.
Table of Content
- Finding the Perimeter of a Triangle
- Introduction
- Basic Concept of Perimeter
- Formula for Perimeter of a Triangle
- Steps to Calculate the Perimeter
- Examples of Calculating Perimeter
- Equilateral Triangle
- Isosceles Triangle
- Scalene Triangle
- Using Coordinates to Find Perimeter
- Application of Distance Formula
- Real-life Applications of Triangle Perimeter
- Common Mistakes to Avoid
- Practice Problems
- YOUTUBE: Hướng dẫn chi tiết về cách tìm chu vi của tam giác, bao gồm các ví dụ và bài tập thực hành.
Finding the Perimeter of a Triangle
The perimeter of a triangle is the total length around the triangle, which can be found by adding up the lengths of its sides.
Formula
The general formula for finding the perimeter (\(P\)) of a triangle with side lengths \(a\), \(b\), and \(c\) is:
\[ P = a + b + c \]
Steps to Find the Perimeter
- Measure the lengths of all three sides of the triangle. Label these lengths as \(a\), \(b\), and \(c\).
- Substitute these values into the formula \( P = a + b + c \).
- Perform the addition to find the perimeter.
Example
Let's say we have a triangle with sides of lengths 5 cm, 7 cm, and 10 cm.
- Identify the side lengths: \( a = 5 \, \text{cm} \), \( b = 7 \, \text{cm} \), \( c = 10 \, \text{cm} \).
- Substitute into the formula: \[ P = 5 + 7 + 10 \]
- Calculate the perimeter: \[ P = 22 \, \text{cm} \]
Special Cases
- Equilateral Triangle: All sides are equal (\( a = b = c \)). The perimeter is \( P = 3a \).
- Isosceles Triangle: Two sides are equal (\( a = b \)). The perimeter is \( P = 2a + c \).
Using Coordinates
If the vertices of the triangle are given as coordinates in the plane, the lengths of the sides can be found using the distance formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
For a triangle with vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the side lengths are:
- \(a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- \(b = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \)
- \(c = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \)
Then, use the formula \( P = a + b + c \) to find the perimeter.
Conclusion
Finding the perimeter of a triangle is a straightforward process that involves measuring the sides and summing their lengths. Whether working with side lengths directly or using coordinate geometry, the key is accurate measurement and calculation.

READ MORE:
Introduction
The perimeter of a triangle is the total distance around the outside of the triangle. It is a fundamental concept in geometry that is widely used in various fields, from construction and engineering to computer graphics and everyday problem-solving. Understanding how to find the perimeter of a triangle is essential for students and professionals alike, as it serves as a building block for more complex geometric principles and applications.
In this comprehensive guide, we will explore the concept of the perimeter, specifically focusing on triangles. We will begin with the basic definition and formula for the perimeter of a triangle, followed by detailed steps to calculate it. Additionally, we will cover special cases such as equilateral, isosceles, and scalene triangles, and demonstrate how to use coordinates to find the perimeter using the distance formula.
Furthermore, we will discuss real-life applications of calculating the perimeter of a triangle, common mistakes to avoid, and provide practice problems to reinforce the concepts learned. By the end of this guide, you will have a thorough understanding of how to calculate the perimeter of various types of triangles and apply this knowledge effectively in practical scenarios.
Basic Concept of Perimeter
The perimeter of any two-dimensional figure is the total distance around its edges. In the case of a polygon, such as a triangle, the perimeter is the sum of the lengths of all its sides.
A triangle is a three-sided polygon with three edges and three vertices. The perimeter of a triangle is calculated by adding the lengths of its three sides. For a triangle with side lengths \(a\), \(b\), and \(c\), the perimeter \(P\) is given by:
\[ P = a + b + c \]
This formula applies to all types of triangles, whether they are equilateral, isosceles, or scalene:
- Equilateral Triangle: All three sides are equal. If each side is \(a\), the perimeter is \(3a\).
- Isosceles Triangle: Two sides are equal. If the equal sides are \(a\) and the base is \(b\), the perimeter is \(2a + b\).
- Scalene Triangle: All three sides are different. The perimeter is the sum of all three sides \(a + b + c\).
In practical terms, calculating the perimeter of a triangle can be done in a few simple steps:
- Measure the lengths of all three sides of the triangle. Ensure that all measurements are in the same unit.
- Add the lengths of the three sides together.
- Express the result in the same units as the side lengths.
For example, if a triangle has sides of lengths 5 cm, 7 cm, and 10 cm, the perimeter is calculated as:
\[ P = 5 \, \text{cm} + 7 \, \text{cm} + 10 \, \text{cm} = 22 \, \text{cm} \]
Understanding the perimeter is essential in various real-life applications, such as determining the amount of material needed to surround a triangular garden or the total length of fencing required for a triangular plot of land.
Formula for Perimeter of a Triangle
The perimeter of a triangle is the total length of its boundary, which is the sum of the lengths of all its sides. This concept applies to all types of triangles, whether they are equilateral, isosceles, or scalene.
To find the perimeter of a triangle, you use the following general formula:
\( P = a + b + c \)
Here, \( P \) represents the perimeter, and \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
Equilateral Triangle
An equilateral triangle has all three sides of equal length. Therefore, the formula for the perimeter simplifies to:
\( P = 3a \)
where \( a \) is the length of one side.
Isosceles Triangle
An isosceles triangle has two sides of equal length. The formula for the perimeter of an isosceles triangle is:
\( P = 2a + b \)
where \( a \) is the length of each of the equal sides, and \( b \) is the length of the base.
Scalene Triangle
A scalene triangle has all sides of different lengths. For a scalene triangle, the general formula for the perimeter is used:
\( P = a + b + c \)
Right Triangle
In a right triangle, one angle is 90 degrees. If the lengths of the legs are \( a \) and \( b \), and the hypotenuse is \( c \), the perimeter can be calculated as:
\( P = a + b + c \)
Often, the hypotenuse is not given directly and needs to be calculated using the Pythagorean theorem:
\( c = \sqrt{a^2 + b^2} \)
Examples
Here are a few examples to illustrate the calculation of the perimeter for different types of triangles:
- For an equilateral triangle with each side measuring 5 cm:
- For an isosceles triangle with the two equal sides measuring 7 cm each and the base measuring 10 cm:
- For a scalene triangle with sides measuring 6 cm, 8 cm, and 10 cm:
- For a right triangle with legs measuring 3 cm and 4 cm:
\( P = 3 \times 5 = 15 \, \text{cm} \)
\( P = 2 \times 7 + 10 = 24 \, \text{cm} \)
\( P = 6 + 8 + 10 = 24 \, \text{cm} \)
First, find the hypotenuse:
\( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{cm} \)
Then, calculate the perimeter:
\( P = 3 + 4 + 5 = 12 \, \text{cm} \)
Steps to Calculate the Perimeter
Calculating the perimeter of a triangle involves adding the lengths of its three sides. Follow these simple steps to find the perimeter of any triangle:
- Identify the Shape: Ensure that the shape in question is a triangle. A triangle has three sides.
- Note Down the Lengths: Measure and write down the lengths of all three sides of the triangle. Ensure that all side lengths are in the same unit.
- Add the Lengths: Add the lengths of the three sides together to find the perimeter. Use the formula:
\[
\text{Perimeter} = a + b + c
\]
where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle. - Assign Units: Ensure that the perimeter is expressed in the same unit as the side lengths. For example, if the sides are measured in meters, the perimeter will also be in meters.
Let's look at an example:
Consider a triangle with side lengths of 5 cm, 7 cm, and 10 cm. To find the perimeter:
- Step 1: Identify the shape as a triangle.
- Step 2: Note the side lengths: \( a = 5 \) cm, \( b = 7 \) cm, \( c = 10 \) cm.
- Step 3: Add the lengths: \( 5 + 7 + 10 = 22 \) cm.
- Step 4: The perimeter of the triangle is 22 cm.
By following these steps, you can easily calculate the perimeter of any triangle, whether it is equilateral, isosceles, or scalene.
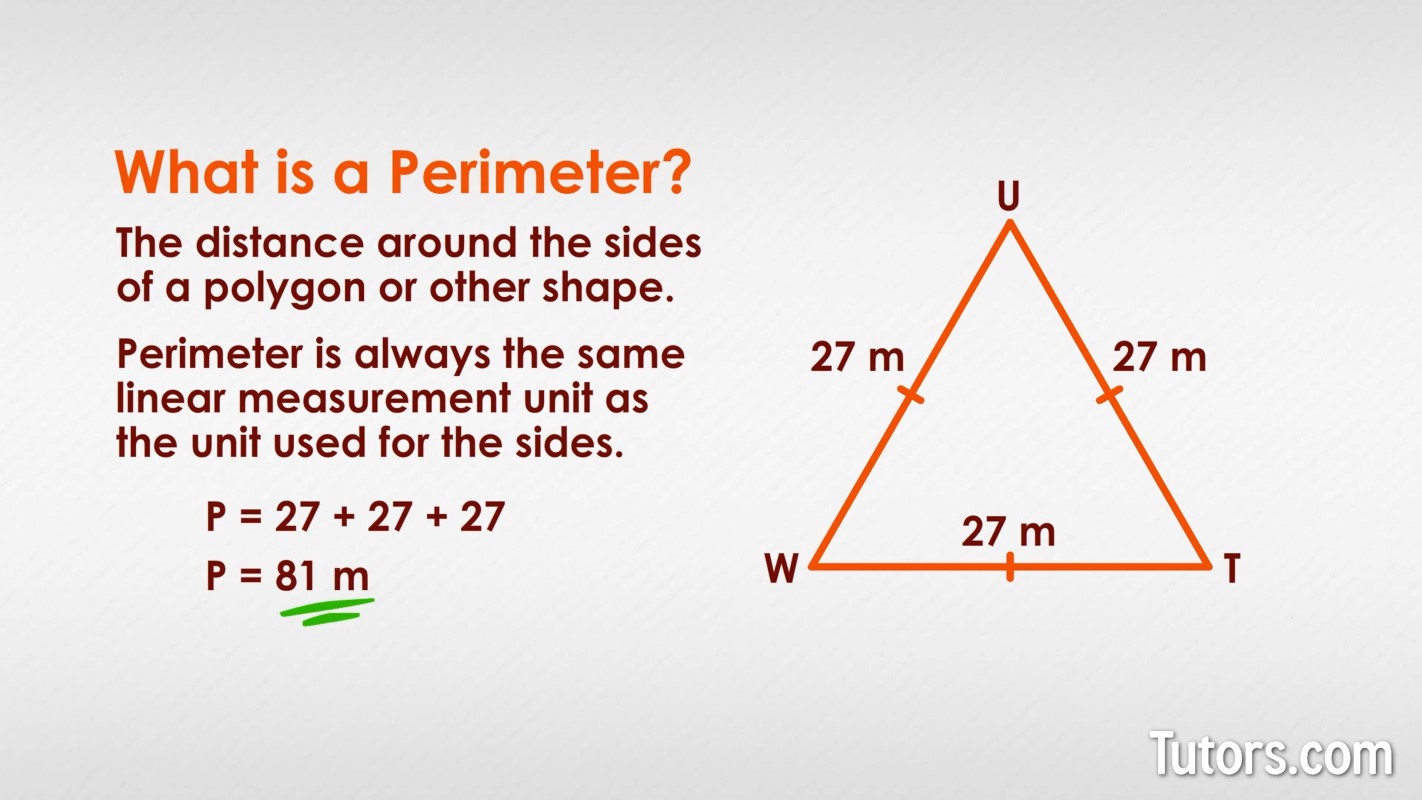
Examples of Calculating Perimeter
To understand how to calculate the perimeter of a triangle, let's go through a few examples involving different types of triangles.
Example 1: Equilateral Triangle
An equilateral triangle has all three sides of equal length.
Consider an equilateral triangle with each side measuring 7 inches.
- Side lengths: \(a = 7 \, \text{inches}\)
- Perimeter \(P\): \(P = 3a\)
- Calculation: \(P = 3 \times 7 = 21 \, \text{inches}\)
Example 2: Isosceles Triangle
An isosceles triangle has two sides of equal length.
Consider an isosceles triangle with two equal sides of 5 feet each and a base of 7 feet.
- Side lengths: \(a = 5 \, \text{feet}, \, b = 5 \, \text{feet}, \, c = 7 \, \text{feet}\)
- Perimeter \(P\): \(P = a + b + c\)
- Calculation: \(P = 5 + 5 + 7 = 17 \, \text{feet}\)
Example 3: Scalene Triangle
A scalene triangle has all three sides of different lengths.
Consider a triangle with side lengths of 3 cm, 4 cm, and 5 cm.
- Side lengths: \(a = 3 \, \text{cm}, \, b = 4 \, \text{cm}, \, c = 5 \, \text{cm}\)
- Perimeter \(P\): \(P = a + b + c\)
- Calculation: \(P = 3 + 4 + 5 = 12 \, \text{cm}\)
Example 4: Right-Angled Triangle
A right-angled triangle has one angle of 90 degrees. The side opposite this angle is the hypotenuse.
Consider a right-angled triangle with the base of 6 units and the height of 8 units.
- Base \(b = 6 \, \text{units}\), Height \(h = 8 \, \text{units}\)
- Using Pythagorean theorem: \( \text{Hypotenuse} \, c = \sqrt{b^2 + h^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \, \text{units}\)
- Perimeter \(P\): \(P = a + b + c\)
- Calculation: \(P = 6 + 8 + 10 = 24 \, \text{units}\)
Example 5: Algebraic Approach
Consider a triangle where the sides are given by algebraic expressions. Let the perimeter of triangle \( \Delta YAK \) be 118 km, with sides:
- \(YA = 2x + 5\)
- \(YK = 6x - 10\)
- \(AK = 4x + 15\)
To find \(x\), we use the perimeter formula:
- \(2x + 5 + 6x - 10 + 4x + 15 = 118\)
- Combine like terms: \(12x + 10 = 118\)
- Solve for \(x\): \(12x = 108\)
- \(x = 9\)
- Substitute \(x\) back into the expressions to find the sides:
- \(YA = 2(9) + 5 = 23 \, \text{km}\)
- \(YK = 6(9) - 10 = 44 \, \text{km}\)
- \(AK = 4(9) + 15 = 51 \, \text{km}\)
- Verify the perimeter: \(23 + 44 + 51 = 118 \, \text{km}\)
Thus, the perimeter calculation is correct.
Equilateral Triangle
An equilateral triangle is a special type of triangle where all three sides are of equal length and all three internal angles are equal to 60 degrees. This symmetry gives the equilateral triangle unique properties and simplifies calculations related to its perimeter, area, and height.
To find the perimeter of an equilateral triangle, you can use the following formula:
Perimeter Formula: \( P = 3a \)
Where \( a \) is the length of one side of the triangle.
Let's go through a detailed example:
- Suppose each side of the equilateral triangle is 10 units.
- Using the formula: \( P = 3 \times 10 = 30 \) units.
The perimeter of this equilateral triangle is 30 units.
Additionally, you can also find the height and area of an equilateral triangle using the following formulas:
Height Formula: \( h = \frac{\sqrt{3}}{2} a \)
Area Formula: \( A = \frac{\sqrt{3}}{4} a^2 \)
These formulas are derived using basic trigonometric principles and the Pythagorean theorem.
For example, if each side of an equilateral triangle is 12 units:
- Calculate the height: \( h = \frac{\sqrt{3}}{2} \times 12 = 6\sqrt{3} \approx 10.39 \) units.
- Calculate the area: \( A = \frac{\sqrt{3}}{4} \times 12^2 = 36\sqrt{3} \approx 62.35 \) square units.
Understanding these properties and formulas allows for quick and accurate calculations related to equilateral triangles, making them a fundamental concept in geometry.
Isosceles Triangle
An isosceles triangle is a triangle with at least two sides of equal length. These two sides are called the legs, and the third side is known as the base. The properties of an isosceles triangle make it a unique and interesting shape to study, especially when calculating its perimeter.
Properties of an Isosceles Triangle
- Two sides (legs) are of equal length.
- The angles opposite the equal sides are also equal.
- The third side is referred to as the base.
Formula for Perimeter of an Isosceles Triangle
To find the perimeter of an isosceles triangle, you can use the following formula:
Let \( a \) be the length of each leg and \( b \) be the length of the base. The perimeter \( P \) of the isosceles triangle is given by:
\( P = 2a + b \)
Steps to Calculate the Perimeter
- Measure the length of one of the equal sides (legs), denoted as \( a \).
- Measure the length of the base, denoted as \( b \).
- Use the formula \( P = 2a + b \) to calculate the perimeter.
Example Calculation
Consider an isosceles triangle with each leg measuring 5 cm and the base measuring 8 cm. The perimeter is calculated as follows:
\( P = 2 \times 5 \, \text{cm} + 8 \, \text{cm} \)
\( P = 10 \, \text{cm} + 8 \, \text{cm} \)
\( P = 18 \, \text{cm} \)
Special Case: Isosceles Right Triangle
An isosceles right triangle is a special type of isosceles triangle where the two equal sides form a right angle. For such triangles:
If the legs are of length \( a \), the base (hypotenuse) can be calculated using the Pythagorean theorem:
\( b = a\sqrt{2} \)
The perimeter \( P \) is then given by:
\( P = 2a + a\sqrt{2} \)
Example Calculation for Isosceles Right Triangle
Consider an isosceles right triangle with legs of length 4 cm. The perimeter is calculated as follows:
\( b = 4\sqrt{2} \, \text{cm} \)
\( P = 2 \times 4 \, \text{cm} + 4\sqrt{2} \, \text{cm} \)
\( P = 8 \, \text{cm} + 4\sqrt{2} \, \text{cm} \)
\( P \approx 8 \, \text{cm} + 5.66 \, \text{cm} \)
\( P \approx 13.66 \, \text{cm} \)
Scalene Triangle
A scalene triangle is a triangle in which all three sides have different lengths. To find the perimeter of a scalene triangle, you simply add the lengths of all three sides together. The formula for the perimeter \( P \) of a scalene triangle with sides \( a \), \( b \), and \( c \) is:
\[ P = a + b + c \]
Here’s a step-by-step method to calculate the perimeter of a scalene triangle:
- Measure the lengths of all three sides of the triangle. Let's denote these lengths as \( a \), \( b \), and \( c \).
- Add the lengths of the sides together using the formula mentioned above.
- The result will be the perimeter of the triangle.
For example, if a scalene triangle has sides measuring 7 cm, 5 cm, and 9 cm, the perimeter calculation would be:
\[ P = 7 \, \text{cm} + 5 \, \text{cm} + 9 \, \text{cm} = 21 \, \text{cm} \]
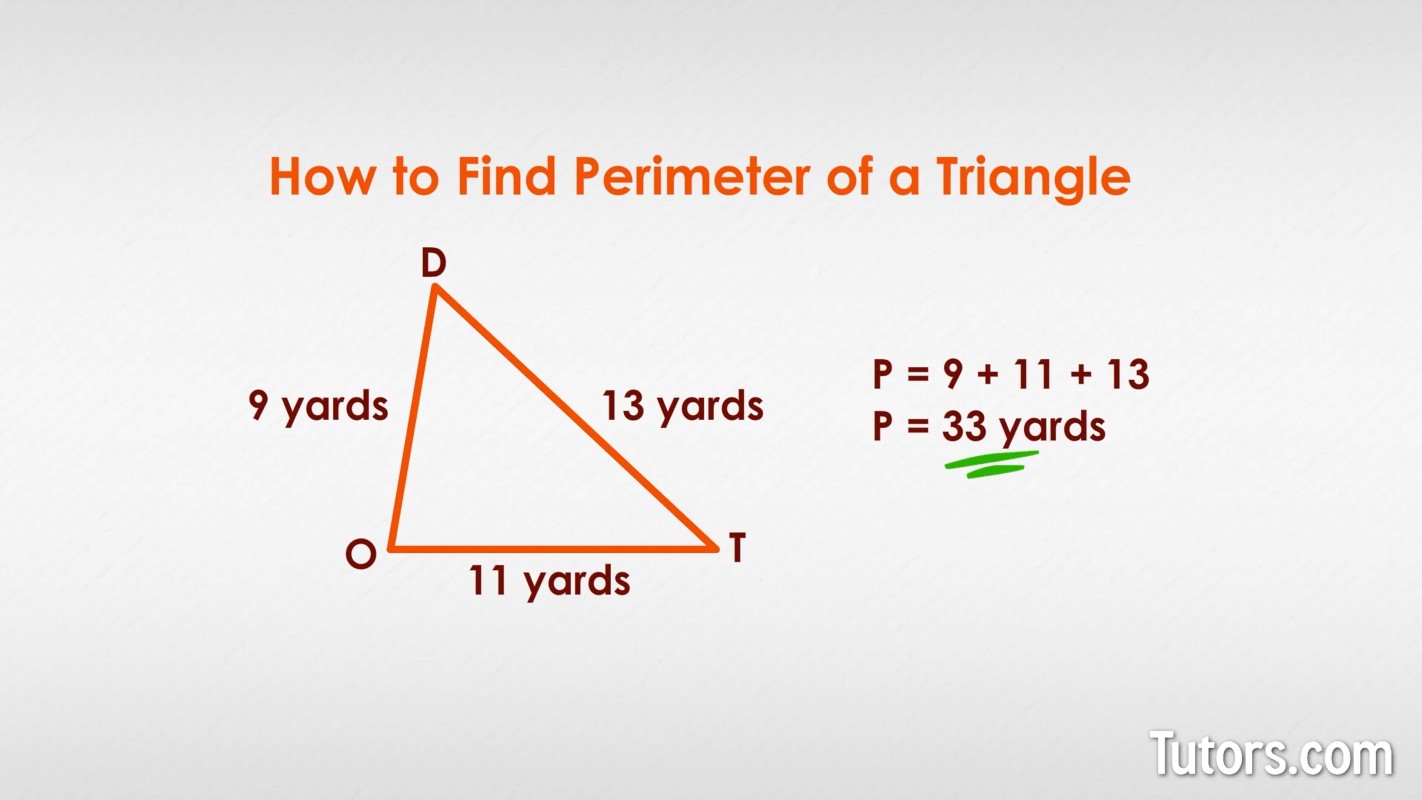
Let's consider another example where a triangle has side lengths of 8 yards, 11 yards, and 13 yards:
\[ P = 8 \, \text{yards} + 11 \, \text{yards} + 13 \, \text{yards} = 32 \, \text{yards} \]
In summary, the process of finding the perimeter of a scalene triangle is straightforward, involving the measurement and addition of its three distinct side lengths.

Using Coordinates to Find Perimeter
To find the perimeter of a triangle using the coordinates of its vertices, we follow these steps:
- Identify the coordinates of the three vertices of the triangle. Let these vertices be \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \).
- Use the distance formula to find the length of each side of the triangle. The distance formula is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Apply this formula to find the distances:
- \( AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- \( BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \)
- \( CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \)
- Add the lengths of the three sides to find the perimeter: \[ \text{Perimeter} = AB + BC + CA \]
Let's go through an example:
Given the vertices \( A(1, 2) \), \( B(4, 5) \), and \( C(4, 0) \):
- Calculate \( AB \): \[ AB = \sqrt{(4 - 1)^2 + (5 - 2)^2} = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} \]
- Calculate \( BC \): \[ BC = \sqrt{(4 - 4)^2 + (0 - 5)^2} = \sqrt{0 + (-5)^2} = \sqrt{25} = 5 \]
- Calculate \( CA \): \[ CA = \sqrt{(4 - 1)^2 + (0 - 2)^2} = \sqrt{3^2 + (-2)^2} = \sqrt{9 + 4} = \sqrt{13} \]
- Find the perimeter: \[ \text{Perimeter} = 3\sqrt{2} + 5 + \sqrt{13} \approx 3(1.41) + 5 + 3.61 = 4.23 + 5 + 3.61 = 12.84 \]
Therefore, the perimeter of the triangle with vertices \( A(1, 2) \), \( B(4, 5) \), and \( C(4, 0) \) is approximately 12.84 units.
Application of Distance Formula
The distance formula is a powerful tool for finding the perimeter of a triangle when the vertices are known in a coordinate plane. The formula is derived from the Pythagorean Theorem and is used to calculate the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\).
The distance formula is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
To find the perimeter of a triangle using the distance formula, follow these steps:
- Identify the coordinates of the three vertices of the triangle. Let's denote these vertices as \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(C(x_3, y_3)\).
- Calculate the length of each side using the distance formula:
- Length of \(AB\): \[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Length of \(BC\): \[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- Length of \(CA\): \[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
- Add the lengths of the three sides to find the perimeter:
\[ \text{Perimeter} = AB + BC + CA \]
Let's consider an example:
Given a triangle with vertices \(A(1, 2)\), \(B(4, 6)\), and \(C(5, 2)\), we can find the perimeter as follows:
- Calculate \(AB\): \[ AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Calculate \(BC\): \[ BC = \sqrt{(5 - 4)^2 + (2 - 6)^2} = \sqrt{1^2 + (-4)^2} = \sqrt{1 + 16} = \sqrt{17} \]
- Calculate \(CA\): \[ CA = \sqrt{(5 - 1)^2 + (2 - 2)^2} = \sqrt{4^2 + 0^2} = \sqrt{16} = 4 \]
- Find the perimeter: \[ \text{Perimeter} = AB + BC + CA = 5 + \sqrt{17} + 4 \]
By following these steps, you can easily apply the distance formula to find the perimeter of any triangle given its vertices in a coordinate plane.
Real-life Applications of Triangle Perimeter
The perimeter of a triangle is a fundamental concept that finds applications in various real-life scenarios. Here are some detailed examples of how calculating the perimeter of a triangle can be useful:
- Construction and Architecture:
In construction and architecture, knowing the perimeter of triangular sections can help in estimating the amount of materials needed, such as fencing, wiring, or framing. For instance, when designing triangular roof trusses or gable ends, accurate perimeter measurements ensure proper material procurement and structural integrity.
- Landscaping:
In landscaping projects, calculating the perimeter of triangular flower beds, lawns, or water features helps in determining the amount of edging material, mulch, or soil required. This ensures precise planning and efficient use of resources.
- Navigation and Surveying:
Surveyors and navigators often work with triangular plots of land or navigational paths. Knowing the perimeter of these triangles is essential for mapping, dividing land, and planning routes. For example, in land surveying, triangular parcels are common, and their perimeters must be calculated to determine boundary lengths and area sizes.
- Sports and Recreation:
In sports, particularly in designing fields and courts, triangles often form part of the layout. For example, the perimeter of triangular areas in a soccer field or a baseball diamond needs to be calculated for proper field marking and maintenance.
- Art and Design:
Artists and designers use triangular shapes in various projects, from graphic design to sculpture. Knowing the perimeter allows for accurate scaling and material use. For example, creating a triangular art installation requires precise perimeter calculations to ensure the stability and proportion of the structure.
- Textile and Fashion Industry:
In the textile and fashion industry, triangular patterns are common in garments and accessories. Calculating the perimeter of these triangles helps in cutting fabric accurately and estimating the amount of material needed, reducing waste and optimizing production.
- Agriculture:
Farmers may use triangular plots for planting due to the shape of the land. Calculating the perimeter of these plots helps in planning irrigation systems, fencing, and the application of fertilizers and pesticides, ensuring efficient farm management.
Common Mistakes to Avoid
When calculating the perimeter of a triangle, several common mistakes can occur. Here are some detailed explanations and steps to avoid these errors:
- Incorrect Identification of Side Lengths:
One of the most frequent mistakes is using incorrect side lengths. Ensure you accurately identify and measure each side of the triangle before performing calculations.
- Ignoring Units of Measurement:
Always pay attention to the units of measurement. Mixing different units (e.g., centimeters and inches) can lead to incorrect results. Ensure all measurements are in the same unit before summing them up.
- Misinterpreting Triangle Types:
Understanding the type of triangle (equilateral, isosceles, or scalene) is crucial. Each type has unique properties:
- Equilateral Triangle: All sides are equal.
- Isosceles Triangle: Two sides are equal.
- Scalene Triangle: All sides are different.
- Incorrect Use of the Distance Formula:
When calculating the perimeter of a triangle with vertices given as coordinates, correctly applying the distance formula is vital. The formula is:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]Ensure each coordinate is correctly substituted into the formula to find the side lengths accurately.
- Rounding Errors:
Be cautious with rounding numbers. Rounding too early in the calculation process can lead to significant inaccuracies. Perform all calculations with full precision and round the final result if necessary.
- Forgetting to Add All Sides:
The perimeter of a triangle is the sum of all its side lengths. It’s a common mistake to omit one side in the final calculation. Double-check to ensure all three sides are included:
\[
P = a + b + c
\] - Misreading Problem Statements:
Carefully read the problem statement to understand what is required. Look out for additional information or constraints that may affect your calculation.
- Incorrectly Assuming Right Angles:
Do not assume a triangle has a right angle unless it is explicitly stated. Right triangles have specific properties that do not apply to other triangle types.
Avoiding these common mistakes will help ensure accurate and reliable calculations of the perimeter of any triangle.
Practice Problems
Practicing problems on finding the perimeter of a triangle will help solidify your understanding of the concepts and formulas involved. Below are some practice problems with step-by-step solutions:
-
Problem 1:
Find the perimeter of a triangle with sides of lengths 5 cm, 7 cm, and 9 cm.
Solution:
- Step 1: Identify the lengths of the sides: \(a = 5 \text{ cm}\), \(b = 7 \text{ cm}\), \(c = 9 \text{ cm}\).
- Step 2: Use the perimeter formula: \[ P = a + b + c \]
- Step 3: Calculate the perimeter: \[ P = 5 + 7 + 9 = 21 \text{ cm} \]
-
Problem 2:
Given a triangle with vertices at coordinates \((1, 2)\), \((4, 6)\), and \((7, 2)\), find the perimeter.
Solution:
- Step 1: Calculate the lengths of each side using the distance formula: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Step 2: Calculate the length of side \(AB\) between \((1, 2)\) and \((4, 6)\): \[ AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Step 3: Calculate the length of side \(BC\) between \((4, 6)\) and \((7, 2)\): \[ BC = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Step 4: Calculate the length of side \(CA\) between \((7, 2)\) and \((1, 2)\): \[ CA = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{6^2 + 0^2} = \sqrt{36} = 6 \]
- Step 5: Add the lengths of all sides to find the perimeter: \[ P = AB + BC + CA = 5 + 5 + 6 = 16 \]
-
Problem 3:
An equilateral triangle has a side length of 8 cm. Find its perimeter.
Solution:
- Step 1: Identify the side length: \(a = 8 \text{ cm}\).
- Step 2: Use the formula for the perimeter of an equilateral triangle: \[ P = 3a \]
- Step 3: Calculate the perimeter: \[ P = 3 \times 8 = 24 \text{ cm} \]
These practice problems cover different types of triangles and scenarios, helping you become proficient in calculating the perimeter of a triangle.
Hướng dẫn chi tiết về cách tìm chu vi của tam giác, bao gồm các ví dụ và bài tập thực hành.
Cách Tìm Chu Vi Của Tam Giác
READ MORE:
Hướng dẫn chi tiết cách tìm chu vi của tam giác cùng thầy J, bao gồm các ví dụ minh họa và bài tập thực hành.
Cách Tìm Chu Vi Của Tam Giác | Toán Học Với Thầy J