Topic formula for perimeter of right triangle: Discover the simple and effective formula for the perimeter of a right triangle. This article guides you through understanding the components and calculations, ensuring you can confidently find the perimeter with ease. Dive into examples, step-by-step instructions, and practical applications to master this fundamental geometric concept.
Table of Content
- Perimeter of a Right Triangle
- Introduction
- Understanding Right Triangles
- Basic Concepts
- Components of a Right Triangle
- Definition of Perimeter
- Formula for Perimeter of a Right Triangle
- Steps to Calculate Perimeter
- Example Calculations
- Special Cases
- Applications in Real Life
- Common Mistakes to Avoid
- Advanced Topics
- Related Mathematical Concepts
- Practice Problems
- Summary
- Frequently Asked Questions (FAQs)
- Additional Resources
- YOUTUBE: Xem video này để học cách tính diện tích và chu vi của tam giác vuông cùng Mr. J, hướng dẫn chi tiết và dễ hiểu cho mọi người.
Perimeter of a Right Triangle
The perimeter of a right triangle is the total length of its three sides. A right triangle consists of two legs, which are perpendicular to each other, and a hypotenuse, which is the side opposite the right angle.
Formula
The formula for the perimeter \( P \) of a right triangle can be expressed as:
\[ P = a + b + c \]
where:
- \( a \) is the length of one leg
- \( b \) is the length of the other leg
- \( c \) is the length of the hypotenuse
Using the Pythagorean Theorem
The hypotenuse \( c \) can be found using the Pythagorean theorem if the lengths of the legs are known:
\[ c = \sqrt{a^2 + b^2} \]
Steps to Calculate the Perimeter
- Measure or find the lengths of both legs (\( a \) and \( b \)).
- Calculate the length of the hypotenuse (\( c \)) using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \]
- Add the lengths of the two legs and the hypotenuse to find the perimeter: \[ P = a + b + c \]
Example
Suppose you have a right triangle with legs of lengths 3 units and 4 units:
- Calculate the hypotenuse: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Calculate the perimeter: \[ P = 3 + 4 + 5 = 12 \text{ units} \]

READ MORE:
Introduction
Welcome to the comprehensive guide on the perimeter of a right triangle. In this guide, we will explore the fundamental concepts, formulas, and applications related to calculating the perimeter of a right triangle. Whether you are a student, educator, or math enthusiast, this guide is designed to provide a thorough understanding of this essential geometric concept.
A right triangle, also known as a right-angled triangle, is a type of triangle that includes one angle measuring 90 degrees. The sides of a right triangle have specific names: the two sides that form the right angle are called the legs, and the side opposite the right angle is known as the hypotenuse.
The perimeter of a right triangle is the total length of its three sides. To calculate the perimeter, one must add the lengths of the two legs and the hypotenuse. Understanding how to find the perimeter of a right triangle is crucial in various fields such as architecture, engineering, and various scientific disciplines.
In this guide, we will cover:
- The basic properties of right triangles.
- Key concepts and definitions related to triangles and their perimeters.
- Step-by-step methods for calculating the perimeter using different approaches.
- Examples and special cases to enhance your understanding.
- Real-life applications and common mistakes to avoid.
By the end of this guide, you will have a solid grasp of the perimeter of right triangles and be able to apply this knowledge to solve various mathematical problems. Let's dive into the fascinating world of right triangles and uncover the secrets of their perimeters!
Understanding Right Triangles
A right triangle, also known as a right-angled triangle, is a type of triangle that has one angle measuring exactly 90 degrees. This unique property makes right triangles a fundamental topic in geometry and trigonometry. Right triangles are used extensively in various fields such as engineering, architecture, physics, and everyday problem-solving.
Here are the key components of a right triangle:
- Legs: The two sides that form the right angle are called the legs of the triangle. These sides are perpendicular to each other.
- Hypotenuse: The side opposite the right angle is known as the hypotenuse. The hypotenuse is always the longest side of a right triangle.
Right triangles can be categorized based on the relative lengths of their legs:
- Isosceles Right Triangle: A right triangle where the two legs are of equal length. In this case, the hypotenuse is \( \sqrt{2} \) times the length of each leg.
- Scalene Right Triangle: A right triangle where all three sides have different lengths.
One of the most important aspects of right triangles is the Pythagorean Theorem, which establishes a relationship between the lengths of the sides:
Here, \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse.
Understanding the properties and formulas related to right triangles is essential for solving various geometric problems and for applications in trigonometry. As we proceed, we will delve deeper into these concepts, providing examples and practical applications to enhance your comprehension.
Basic Concepts
Understanding the basic concepts related to right triangles is crucial for grasping more advanced topics. Here, we will cover the essential elements and properties of right triangles, which will serve as a foundation for calculating their perimeter and solving related problems.
1. Sides of a Right Triangle:
- Legs: The two sides that form the right angle. These are usually denoted as \(a\) and \(b\).
- Hypotenuse: The side opposite the right angle. This is the longest side of the right triangle and is denoted as \(c\).
2. Pythagorean Theorem:
The Pythagorean Theorem is a fundamental principle that relates the lengths of the sides of a right triangle. It states that:
This theorem allows us to calculate the length of one side if the lengths of the other two sides are known.
3. Perimeter of a Right Triangle:
The perimeter of a right triangle is the sum of the lengths of its three sides. The formula to calculate the perimeter \(P\) is:
\( P = a + b + c \)
4. Area of a Right Triangle:
The area \(A\) of a right triangle can be calculated using the formula:
\( A = \frac{1}{2} \times a \times b \)
This formula is derived from the fact that a right triangle can be considered as half of a rectangle.
5. Special Right Triangles:
There are certain right triangles with specific angle measures that have unique properties:
- 45°-45°-90° Triangle: An isosceles right triangle where the legs are of equal length. The hypotenuse is \( \sqrt{2} \) times the length of each leg.
- 30°-60°-90° Triangle: A right triangle where the lengths of the sides are in the ratio 1:\(\sqrt{3}\):2. The hypotenuse is twice the length of the shorter leg, and the longer leg is \( \sqrt{3} \) times the length of the shorter leg.
By understanding these basic concepts, you will be well-prepared to tackle more complex problems involving right triangles. In the following sections, we will build on this knowledge and explore the perimeter of right triangles in greater detail.
Components of a Right Triangle
A right triangle is characterized by having one angle that is exactly 90 degrees. This unique property defines the components of a right triangle, each playing a crucial role in its geometric properties and calculations. Understanding these components is essential for solving problems related to right triangles.
The primary components of a right triangle include:
- Legs: The two sides that form the right angle. These sides are perpendicular to each other.
- Adjacent Leg (Base): The leg adjacent to the angle of interest in trigonometric calculations.
- Opposite Leg (Height): The leg opposite the angle of interest in trigonometric calculations.
- Hypotenuse: The side opposite the right angle, which is the longest side of the right triangle.
Here is a detailed breakdown of these components:
1. Legs:
The legs of a right triangle are the two sides that create the 90-degree angle. These are usually referred to as:
- Leg \(a\): One of the legs of the triangle.
- Leg \(b\): The other leg of the triangle.
In a coordinate system, if one leg is aligned with the x-axis and the other with the y-axis, they can be easily measured as the horizontal and vertical distances between points.
2. Hypotenuse:
The hypotenuse is the side opposite the right angle and is denoted as \(c\). It is the longest side in a right triangle. The length of the hypotenuse can be calculated using the Pythagorean Theorem:
Thus, \(c = \sqrt{a^2 + b^2}\).
3. Angles:
In addition to the right angle, a right triangle has two other angles. These angles are complementary, meaning their measures add up to 90 degrees. If one angle is denoted as \( \theta \), the other angle will be \( 90^\circ - \theta \).
Understanding these components is fundamental for performing various calculations involving right triangles, such as finding the perimeter, area, and applying trigonometric ratios. In the next sections, we will explore the perimeter calculation in detail, using these components effectively.
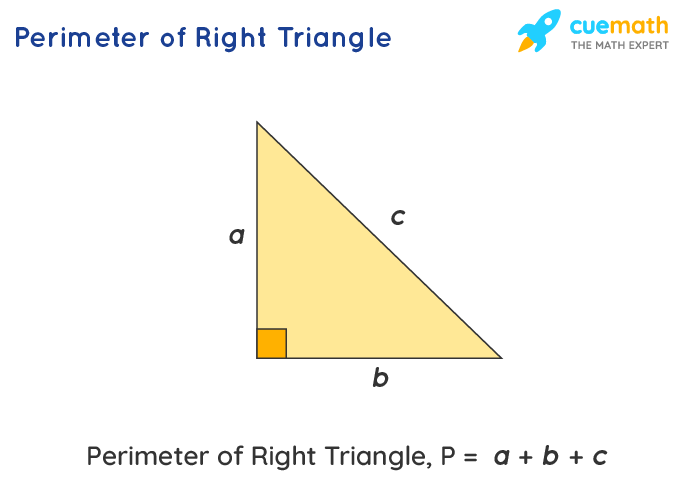
Definition of Perimeter
The perimeter of a geometric figure is the total length around the figure. For a triangle, the perimeter is the sum of the lengths of all its sides. When it comes to a right triangle, this calculation involves adding the lengths of the two legs and the hypotenuse.
Mathematically, the perimeter \(P\) of a right triangle can be defined using the lengths of its three sides: the two legs \(a\) and \(b\), and the hypotenuse \(c\). The formula to calculate the perimeter is straightforward:
\( P = a + b + c \)
Here's a step-by-step explanation of this formula:
- Measure the lengths of the two legs \(a\) and \(b\) of the right triangle.
- Calculate the length of the hypotenuse \(c\) using the Pythagorean Theorem if it is not already known:
Therefore, \(c = \sqrt{a^2 + b^2}\).
- Add the lengths of the two legs and the hypotenuse to find the perimeter:
\( P = a + b + c \)
For example, if a right triangle has legs of lengths 3 units and 4 units, and a hypotenuse of 5 units, the perimeter is calculated as follows:
\( P = 3 + 4 + 5 = 12 \) units
Understanding the perimeter of a right triangle is essential for various applications in mathematics, engineering, and real-life scenarios, such as determining the amount of material needed to frame a triangular area or finding the total distance around a triangular path.
Formula for Perimeter of a Right Triangle
Calculating the perimeter of a right triangle involves summing the lengths of its three sides: the two legs and the hypotenuse. The formula for the perimeter \(P\) of a right triangle is given by:
\( P = a + b + c \)
Here, \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse. To provide a comprehensive understanding, let's break down the process step by step:
- Identify the lengths of the legs:
The legs of the right triangle are the two sides that form the right angle. These are typically denoted as \(a\) and \(b\).
- Calculate the hypotenuse:
Using the Pythagorean Theorem, the hypotenuse \(c\) can be calculated if it is not already known:
Therefore, \(c = \sqrt{a^2 + b^2}\).
- Add the lengths of all three sides:
Once the lengths of the legs \(a\) and \(b\), and the hypotenuse \(c\) are known, sum them to find the perimeter:
\( P = a + b + c \)
For example, consider a right triangle with legs of lengths 3 units and 4 units. First, calculate the hypotenuse:
\( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units
Then, add the lengths of the legs and the hypotenuse to find the perimeter:
\( P = 3 + 4 + 5 = 12 \) units
This step-by-step method ensures accurate calculation of the perimeter, which is essential for various practical applications such as construction, navigation, and design. Understanding and applying this formula is fundamental for solving problems involving right triangles.
Steps to Calculate Perimeter
Calculating the perimeter of a right triangle involves a straightforward process of adding the lengths of its three sides. Here are the detailed steps to determine the perimeter:
- Identify the lengths of the legs:
Determine the lengths of the two legs of the right triangle, denoted as \(a\) and \(b\). These are the sides that form the right angle.
- Calculate the hypotenuse:
If the hypotenuse \(c\) is not already known, use the Pythagorean Theorem to calculate it:
Therefore, \(c = \sqrt{a^2 + b^2}\).
- Sum the lengths of all three sides:
Add the lengths of the two legs and the hypotenuse to find the perimeter \(P\):
\( P = a + b + c \)
Let's go through an example to illustrate these steps:
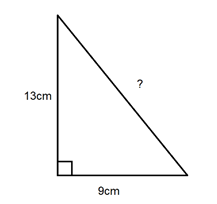
- Suppose the lengths of the legs of a right triangle are \(a = 5\) units and \(b = 12\) units.
- First, calculate the hypotenuse \(c\):
\( c = \sqrt{169} = 13 \) units
- Then, find the perimeter by summing all three sides:
\( P = 5 + 12 + 13 = 30 \) units
By following these steps, you can accurately determine the perimeter of any right triangle. This method is essential for solving various mathematical problems and is widely applicable in real-world situations, such as construction, navigation, and design.
Example Calculations
In this section, we will go through some example calculations to find the perimeter of right triangles. The formula for the perimeter of a right triangle is:
Perimeter (P) = a + b + c
where a and b are the legs of the right triangle, and c is the hypotenuse.
Example 1
Given a right triangle with legs a = 3 units and b = 4 units, calculate the perimeter.
- First, use the Pythagorean theorem to find the hypotenuse c:
- Now, calculate the perimeter:
\[
c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units}
\]
\[
P = a + b + c = 3 + 4 + 5 = 12 \text{ units}
\]
Example 2
Given a right triangle with legs a = 5 units and b = 12 units, calculate the perimeter.
- First, use the Pythagorean theorem to find the hypotenuse c:
- Now, calculate the perimeter:
\[
c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ units}
\]
\[
P = a + b + c = 5 + 12 + 13 = 30 \text{ units}
\]
Example 3
Given a right triangle with legs a = 8 units and b = 15 units, calculate the perimeter.
- First, use the Pythagorean theorem to find the hypotenuse c:
- Now, calculate the perimeter:
\[
c = \sqrt{a^2 + b^2} = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17 \text{ units}
\]
\[
P = a + b + c = 8 + 15 + 17 = 40 \text{ units}
\]
Example 4
Given a right triangle with legs a = 7 units and b = 24 units, calculate the perimeter.
- First, use the Pythagorean theorem to find the hypotenuse c:
- Now, calculate the perimeter:
\[
c = \sqrt{a^2 + b^2} = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \text{ units}
\]
\[
P = a + b + c = 7 + 24 + 25 = 56 \text{ units}
\]
Example 5
Given a right triangle with legs a = 9 units and b = 40 units, calculate the perimeter.
- First, use the Pythagorean theorem to find the hypotenuse c:
- Now, calculate the perimeter:
\[
c = \sqrt{a^2 + b^2} = \sqrt{9^2 + 40^2} = \sqrt{81 + 1600} = \sqrt{1681} = 41 \text{ units}
\]
\[
P = a + b + c = 9 + 40 + 41 = 90 \text{ units}
\]

Special Cases
In some situations, right triangles have properties that make calculations simpler. These are known as special right triangles. The two most common special right triangles are the 45°-45°-90° triangle and the 30°-60°-90° triangle. There are also Pythagorean triples, which are right triangles with integer side lengths.
45°-45°-90° Triangle
A 45°-45°-90° triangle is an isosceles right triangle, meaning its two legs are of equal length. The ratio of the sides in this triangle is:
- Legs: \( x \)
- Hypotenuse: \( x\sqrt{2} \)
For example, if the length of one leg is 5 units, the hypotenuse can be calculated as:
\[
\text{Hypotenuse} = 5\sqrt{2} \approx 7.07 \text{ units}
\]
30°-60°-90° Triangle
A 30°-60°-90° triangle is a right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The sides of this triangle are in the ratio:
- Shortest leg (opposite the 30° angle): \( x \)
- Longest leg (opposite the 60° angle): \( x\sqrt{3} \)
- Hypotenuse: \( 2x \)
For example, if the shortest leg is 4 units, the other sides can be calculated as:
\[
\text{Longest leg} = 4\sqrt{3} \approx 6.93 \text{ units}
\]
\[
\text{Hypotenuse} = 2 \times 4 = 8 \text{ units}
\]
Pythagorean Triples
Pythagorean triples are sets of three positive integers that fit the Pythagorean theorem: \( a^2 + b^2 = c^2 \). Common examples include:
- (3, 4, 5)
- (5, 12, 13)
- (7, 24, 25)
These triples are useful because they allow for quick and easy calculations without needing to use the square root function. For instance, in a 3-4-5 triangle, the perimeter is simply:
\[
3 + 4 + 5 = 12 \text{ units}
\]
Understanding these special cases simplifies the process of solving right triangle problems and helps in various applications in geometry and real-life scenarios.
Applications in Real Life
The perimeter of a right triangle has various applications in real life, often found in fields such as architecture, engineering, and navigation. Understanding how to calculate the perimeter can help solve practical problems and optimize designs. Here are some examples:
1. Architecture and Construction
Right triangles are commonly used in the design and construction of buildings. For example:
- Roof Trusses: Roof trusses often incorporate right triangles to provide structural stability and support. Calculating the perimeter helps in determining the amount of material needed.
- Staircases: The dimensions of staircases are based on right triangles, ensuring safety and comfort. Knowing the perimeter helps in the accurate measurement of railings and banisters.
2. Engineering
Engineering projects frequently use right triangles for various purposes:
- Bridge Trusses: Right triangles in bridge trusses distribute weight and provide strength to the structure. Calculating the perimeter ensures precise fitting of components.
- Ramps: Ramps, which are inclined planes, form right triangles with the ground and the vertical support. The perimeter calculation aids in designing ramps that meet accessibility standards.
3. Navigation and Surveying
Right triangles are essential in navigation and land surveying:
- Measuring Heights: Surveyors use right triangles to measure the height of objects such as buildings or trees by calculating the distance from the base and the angle of elevation.
- GPS Technology: Right triangle principles are used in GPS technology to determine the shortest paths and distances between points on the Earth's surface.
4. Everyday Examples
Right triangles appear in various everyday situations:
- Sports and Recreation: Skateboard ramps and slides are designed using right triangles to ensure proper angles and heights for safety and performance.
- Sails on Boats: The sails of boats are often triangular, and understanding their perimeter helps in adjusting the sails for optimal performance.
- Ladders: When a ladder leans against a wall, it forms a right triangle. Knowing the perimeter ensures the ladder is at a safe angle.
In conclusion, the calculation of the perimeter of right triangles is not just a mathematical exercise but a practical tool that enhances safety, efficiency, and functionality in various aspects of daily life.
Common Mistakes to Avoid
When calculating the perimeter of a right triangle, it is essential to avoid common mistakes that can lead to incorrect results. Here are some common errors and tips to avoid them:
- Incorrectly Identifying the Hypotenuse:
Remember, the hypotenuse is always the side opposite the right angle and is the longest side of the triangle. Misidentifying the hypotenuse can lead to errors in both calculations and understanding of the problem.
- Forgetting to Apply the Pythagorean Theorem Correctly:
When only two sides of the triangle are known, use the Pythagorean theorem \(a^2 + b^2 = c^2\) to find the third side. Ensure you square the lengths of the two known sides and sum them to find the square of the hypotenuse.
- Incorrect Calculation of Square Roots:
Errors often occur when finding the square root of the sum obtained from the Pythagorean theorem. Double-check calculations to ensure accuracy, especially when dealing with non-integer results.
- Neglecting Units:
Always ensure that all measurements are in the same unit before performing any calculations. Mixing units can lead to incorrect perimeter values.
- Rounding Errors:
Be careful with rounding intermediate steps, as it can lead to significant errors in the final result. If possible, keep values in their exact form until the final calculation.
- Using Incorrect Formulas:
Ensure you are using the correct formula for the perimeter of a right triangle: \( P = a + b + c \), where \(a\) and \(b\) are the legs, and \(c\) is the hypotenuse.
By being mindful of these common mistakes and carefully applying the correct mathematical principles, you can accurately calculate the perimeter of right triangles.
Advanced Topics
Exploring the perimeter of right triangles leads us to several advanced mathematical concepts and applications. Here, we delve into a few of these topics:
Pythagorean Triples
Pythagorean triples are sets of three positive integers \(a\), \(b\), and \(c\) that satisfy the equation \(a^2 + b^2 = c^2\). These triples represent the sides of right triangles with integer lengths. For example, (3, 4, 5) and (5, 12, 13) are well-known Pythagorean triples.
- Primitive Pythagorean triples: These are triples where \(a\), \(b\), and \(c\) are coprime (i.e., their greatest common divisor is 1).
- Generating triples: Primitive triples can be generated using formulas involving two positive integers \(m\) and \(n\) where \(m > n\):
- \(a = m^2 - n^2\)
- \(b = 2mn\)
- \(c = m^2 + n^2\)
Special Right Triangles
Certain right triangles have side length ratios that are useful in various applications:
- Isosceles Right Triangle (45°-45°-90°): The sides are in the ratio \(1:1:\sqrt{2}\). If the legs are of length \(a\), then the hypotenuse is \(a\sqrt{2}\).
- 30°-60°-90° Triangle: The sides are in the ratio \(1:\sqrt{3}:2\). If the shortest leg is \(a\), then the hypotenuse is \(2a\) and the longer leg is \(a\sqrt{3}\).
Right Triangle in Coordinate Geometry
Right triangles play a crucial role in coordinate geometry, especially in determining distances between points and in defining slopes.
- Distance Formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is derived from the Pythagorean theorem: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Slope: The slope of a line connecting two points \((x_1, y_1)\) and \((x_2, y_2)\) is: \[ m = \frac{y_2 - y_1}{x_2 - x_1} \] This concept is fundamental in understanding right triangles formed in the coordinate plane.
Trigonometric Ratios and Functions
Right triangles are the foundation of trigonometry. The primary trigonometric ratios—sine, cosine, and tangent—are defined based on the sides of a right triangle.
- \(\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\)
- \(\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}\)
- \(\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}\)
Applications in Real World
Advanced understanding of right triangles is used in various fields such as engineering, physics, architecture, and computer graphics.
- In architecture and construction, right triangles are used to ensure structures are level and stable.
- In navigation and GPS technology, the principles of right triangles help in calculating distances and positions.
- In computer graphics, right triangles are fundamental in rendering and modeling objects.
Exploring these advanced topics provides a deeper appreciation of the versatile applications of right triangles in both theoretical and practical contexts.
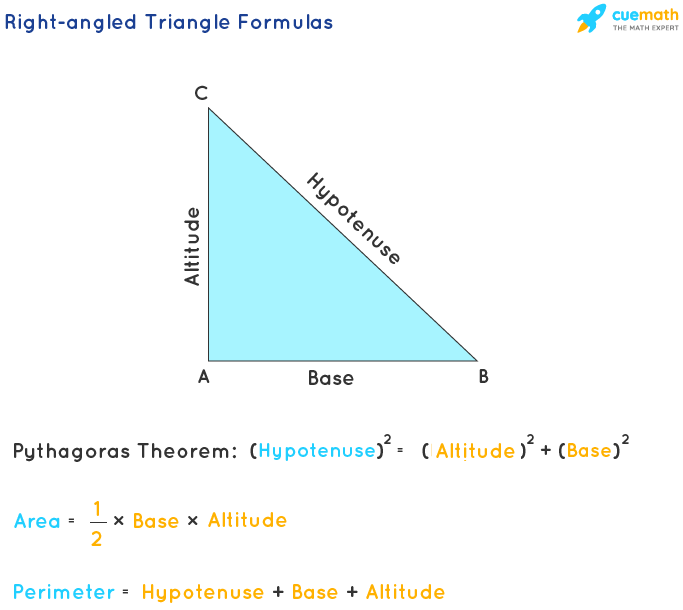
Related Mathematical Concepts
The perimeter of a right triangle is closely related to several fundamental mathematical concepts. Understanding these related concepts can provide deeper insights and help solve more complex problems involving right triangles.
Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry, applicable to right triangles. It states:
where is the hypotenuse, and and are the other two sides.
Trigonometric Ratios
Trigonometric functions such as sine, cosine, and tangent are essential in studying right triangles:
- Sine:
- Cosine:
- Tangent:
Special Right Triangles
Special right triangles, like the 45°-45°-90° and 30°-60°-90° triangles, have unique properties that simplify calculations:
- 45°-45°-90° Triangle: The legs are equal, and the hypotenuse is the leg length times .
- 30°-60°-90° Triangle: The hypotenuse is twice the shorter leg, and the longer leg is the shorter leg times .
Similarity and Congruence
Right triangles can be analyzed through the principles of similarity and congruence. Triangles are similar if their corresponding angles are equal and their sides are proportional. Congruence means the triangles are identical in shape and size.
Coordinate Geometry
In coordinate geometry, right triangles play a crucial role in distance calculations and determining slopes. The distance formula, derived from the Pythagorean Theorem, is used to calculate the distance between two points:
Vectors
Vectors and their magnitudes are often calculated using right triangles. The magnitude of a vector with components is given by:
These related mathematical concepts not only help in understanding right triangles but also form the foundation for various applications in geometry, trigonometry, and beyond.
Practice Problems
To reinforce your understanding of calculating the perimeter of right triangles, here are several practice problems. These problems will involve using the Pythagorean theorem and the perimeter formula.
-
Given a right triangle with legs of lengths 3 cm and 4 cm, find the perimeter of the triangle.
Solution:
- Find the hypotenuse using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) cm
- Calculate the perimeter: \( P = a + b + c = 3 + 4 + 5 = 12\) cm
A right triangle has one leg of 6 inches and a hypotenuse of 10 inches. Find the length of the other leg and the perimeter.
Solution:
- Let the unknown leg be \(b\). Using the Pythagorean theorem: \(10^2 = 6^2 + b^2\)
\(100 = 36 + b^2\)
\(b^2 = 64\)
\(b = \sqrt{64} = 8\) inches - Calculate the perimeter: \( P = a + b + c = 6 + 8 + 10 = 24\) inches
- Let the unknown leg be \(b\). Using the Pythagorean theorem: \(10^2 = 6^2 + b^2\)
Find the perimeter of a right triangle where one leg is 8 m and the other leg is 15 m.
Solution:
- Find the hypotenuse using the Pythagorean theorem: \(c = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17\) m
- Calculate the perimeter: \( P = a + b + c = 8 + 15 + 17 = 40\) m
A right triangle has a hypotenuse of 13 cm and one leg of 5 cm. Find the length of the other leg and the perimeter.
Solution:
- Let the unknown leg be \(b\). Using the Pythagorean theorem: \(13^2 = 5^2 + b^2\)
\(169 = 25 + b^2\)
\(b^2 = 144\)
\(b = \sqrt{144} = 12\) cm - Calculate the perimeter: \( P = a + b + c = 5 + 12 + 13 = 30\) cm
- Let the unknown leg be \(b\). Using the Pythagorean theorem: \(13^2 = 5^2 + b^2\)
Find the perimeter of a right triangle where the legs are 9 ft and 12 ft.
Solution:
- Find the hypotenuse using the Pythagorean theorem: \(c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15\) ft
- Calculate the perimeter: \( P = a + b + c = 9 + 12 + 15 = 36\) ft
Practice these problems to get a solid understanding of calculating the perimeter of right triangles using both the basic perimeter formula and the Pythagorean theorem.
Summary
The perimeter of a right triangle is the sum of the lengths of its three sides. Given a right triangle with sides \(a\), \(b\), and \(c\) (where \(c\) is the hypotenuse), the perimeter \(P\) is calculated as:
\[ P = a + b + c \]
To find the hypotenuse when only the two legs are known, we use the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
Thus, the formula for the perimeter can also be written as:
\[ P = a + b + \sqrt{a^2 + b^2} \]
In summary, calculating the perimeter of a right triangle involves the following steps:
- Identify the lengths of the two legs and the hypotenuse.
- If the hypotenuse is not given, use the Pythagorean theorem to calculate it.
- Add the lengths of the three sides to find the perimeter.
Understanding the perimeter formula and its application is fundamental in various real-life scenarios such as construction, navigation, and any context involving right-angled measurements.
With this knowledge, you can confidently solve problems related to the perimeter of right triangles and apply these principles to more complex geometrical figures and real-world applications.
Frequently Asked Questions (FAQs)
-
What is the formula for the perimeter of a right triangle?
The formula for the perimeter of a right triangle is given by the sum of the lengths of its three sides:
\( P = a + b + c \), where \( a \) and \( b \) are the legs, and \( c \) is the hypotenuse. -
How do you find the hypotenuse of a right triangle?
You can find the hypotenuse using the Pythagorean Theorem, which states:
\( c = \sqrt{a^2 + b^2} \) -
Can the perimeter of a right triangle be calculated without the hypotenuse?
Yes, you can use the Pythagorean Theorem to find the hypotenuse first and then add the lengths of all three sides to find the perimeter.
-
What units are used for the perimeter of a right triangle?
The units for the perimeter are the same as the units used for the sides of the triangle, typically centimeters (cm), meters (m), inches (in), etc.
-
Can a right triangle have a perimeter of zero?
No, a right triangle cannot have a perimeter of zero because all sides must have positive lengths.
-
How can I use the perimeter formula in real-life applications?
The perimeter formula is useful in various applications such as construction, navigation, and any field requiring precise measurements of triangular areas.
-
Are there any special cases for calculating the perimeter of a right triangle?
Special cases include right isosceles triangles where the two legs are equal in length, simplifying the perimeter calculation to \( P = a + a + \sqrt{2a^2} \).
-
What are common mistakes to avoid when calculating the perimeter?
Common mistakes include incorrectly identifying the hypotenuse, not using the same units for all sides, and arithmetic errors in summing the side lengths.
Additional Resources
For further learning and to deepen your understanding of the perimeter of right triangles, consider exploring the following resources:
- : A comprehensive video tutorial on calculating the perimeter of right triangles using the Pythagorean theorem.
- : An interactive page explaining the Pythagorean theorem with examples and practice problems.
- : Detailed lessons and explanations on the Pythagorean theorem and its applications in finding the perimeter of right triangles.
- : A thorough guide to understanding the perimeter of various types of triangles, including right triangles, with interactive examples.
- : A detailed lesson plan covering the perimeter and area of right triangles, suitable for self-study or classroom use.
These resources provide a range of instructional materials, from video tutorials and interactive lessons to in-depth articles and practice problems, all aimed at enhancing your understanding of the perimeter of right triangles.
Xem video này để học cách tính diện tích và chu vi của tam giác vuông cùng Mr. J, hướng dẫn chi tiết và dễ hiểu cho mọi người.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán Học cùng Mr. J
READ MORE:
Hướng dẫn cách tìm diện tích và chu vi của tam giác vuông, giải thích chi tiết và dễ hiểu cho người học.
Cách Tìm Diện Tích và Chu Vi của Tam Giác Vuông