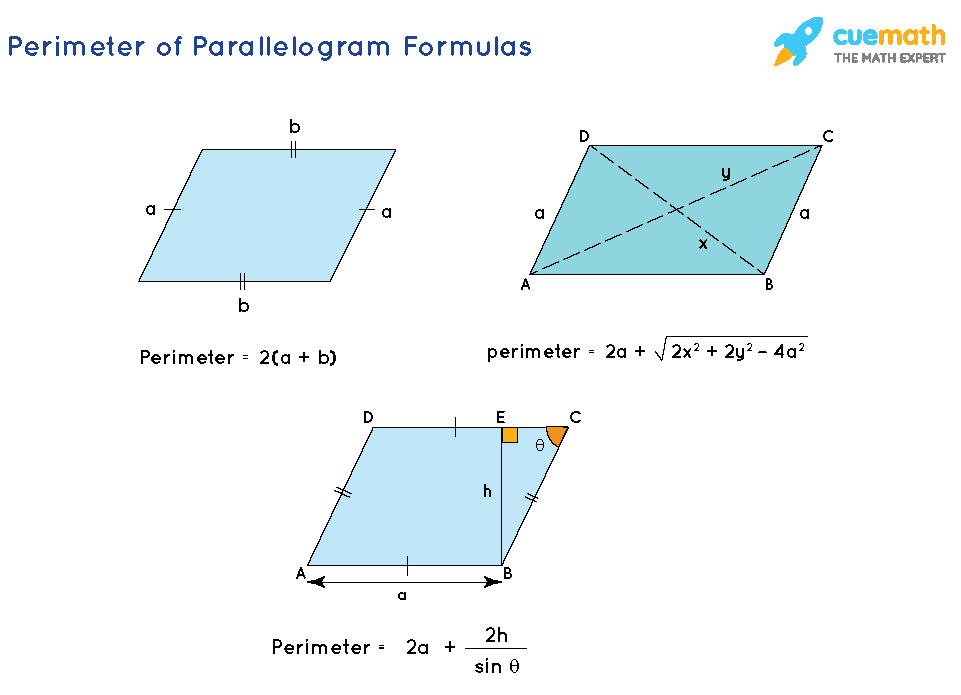
Topic formula for right triangle perimeter: Discover the simple formula for calculating the perimeter of a right triangle. This guide provides easy-to-follow steps and practical examples to help you understand and apply the perimeter formula effectively. Whether you're a student or just looking to refresh your knowledge, this article makes learning straightforward and enjoyable.
Table of Content
- Formula for Right Triangle Perimeter
- Introduction to Right Triangle Perimeter
- Understanding Right Triangles
- Components of a Right Triangle
- Basic Perimeter Formula
- Pythagorean Theorem
- Deriving the Hypotenuse
- Step-by-Step Calculation of Perimeter
- Example Calculations
- Applications of Right Triangle Perimeter
- Common Mistakes to Avoid
- Advanced Concepts
- Practice Problems
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Tìm hiểu về diện tích và chu vi của tam giác vuông với Thầy J. Video này sẽ hướng dẫn bạn cách tính diện tích và chu vi một cách chi tiết và dễ hiểu.
Formula for Right Triangle Perimeter
A right triangle has one angle of 90 degrees. The sides of a right triangle include the two legs (a and b) and the hypotenuse (c). The perimeter of a right triangle is the sum of the lengths of its three sides.
Perimeter Formula
The formula to calculate the perimeter \(P\) of a right triangle is given by:
\[
P = a + b + c
\]
Finding the Hypotenuse
To find the hypotenuse \(c\), use the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]
Steps to Calculate the Perimeter
- Measure the lengths of the two legs \(a\) and \(b\).
- Calculate the hypotenuse \(c\) using the formula:
\[
c = \sqrt{a^2 + b^2}
\] - Add the lengths of all three sides to get the perimeter:
\[
P = a + b + c
\]
Example Calculation
Consider a right triangle with legs \(a = 3\) and \(b = 4\):
- Calculate the hypotenuse:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Calculate the perimeter:
\[
P = 3 + 4 + 5 = 12
\]
Summary
The perimeter of a right triangle is found by summing the lengths of the two legs and the hypotenuse. Using the Pythagorean theorem to find the hypotenuse first ensures an accurate calculation of the perimeter.

READ MORE:
Introduction to Right Triangle Perimeter
Understanding Right Triangles
Components of a Right Triangle
Basic Perimeter Formula
Pythagorean Theorem
Deriving the Hypotenuse
Step-by-Step Calculation of Perimeter
The perimeter of a right triangle is the sum of the lengths of its three sides: the two legs and the hypotenuse. Follow these steps to calculate it:
- Identify the lengths of the two legs of the right triangle, denoted as \( a \) and \( b \).
- Calculate the length of the hypotenuse \( c \) using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\] - Sum the lengths of the legs and the hypotenuse to find the perimeter \( P \):
\[
P = a + b + c
\]
Here is an example to illustrate the process:
- Suppose the lengths of the legs are \( a = 3 \) and \( b = 4 \).
- Calculate the hypotenuse:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Calculate the perimeter:
\[
P = 3 + 4 + 5 = 12
\]
By following these steps, you can easily determine the perimeter of any right triangle.
Example Calculations
Let's look at some examples to better understand how to calculate the perimeter of a right triangle.
Example 1
- Given the legs of the right triangle: \( a = 5 \) and \( b = 12 \).
- Calculate the hypotenuse \( c \):
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13
\] - Calculate the perimeter \( P \):
\[
P = a + b + c = 5 + 12 + 13 = 30
\]
Example 2
- Given the legs of the right triangle: \( a = 8 \) and \( b = 15 \).
- Calculate the hypotenuse \( c \):
\[
c = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17
\] - Calculate the perimeter \( P \):
\[
P = a + b + c = 8 + 15 + 17 = 40
\]
Example 3
- Given the legs of the right triangle: \( a = 7 \) and \( b = 24 \).
- Calculate the hypotenuse \( c \):
\[
c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25
\] - Calculate the perimeter \( P \):
\[
P = a + b + c = 7 + 24 + 25 = 56
\]
These examples demonstrate how to calculate the perimeter of a right triangle using the lengths of its legs and the hypotenuse.

Applications of Right Triangle Perimeter
The perimeter of a right triangle is useful in various practical and theoretical applications. Here are some key areas where this calculation is applied:
Architectural Design
In architecture, the perimeter of right triangles is used to determine the lengths of materials needed for construction projects, such as framing, roofing, and creating triangular structures. Accurate perimeter calculations ensure that the correct amount of materials is used, minimizing waste and cost.
Land Surveying
Land surveyors often use right triangles to measure distances and plot land features. By calculating the perimeter of these triangles, they can determine property boundaries and create accurate maps.
Navigation and Mapping
In navigation, especially in marine and aerial contexts, right triangle calculations help in charting courses and determining distances between waypoints. The perimeter helps in planning the most efficient routes and ensuring accurate navigation.
Trigonometry and Mathematics
The study of right triangles and their perimeters is fundamental in trigonometry. Understanding these principles is crucial for solving more complex mathematical problems and proving various theorems in geometry.
Engineering
Engineers use right triangle perimeter calculations in designing and analyzing structures, bridges, and various mechanical systems. These calculations ensure that the designs are both efficient and safe, providing the necessary support and stability.
Art and Design
In art and design, right triangles are used to create aesthetically pleasing compositions and structures. The perimeter helps in determining the proportions and scaling of different elements within a design.
Real-Life Problem Solving
Beyond specific fields, the principles of calculating the perimeter of right triangles are applied in everyday problem-solving scenarios. Whether it's determining the length of a garden path or designing a piece of furniture, these calculations are practical and widely applicable.
Overall, the ability to calculate the perimeter of right triangles is an essential skill with broad applications in many disciplines. Mastery of this concept provides a strong foundation for further study and practical problem-solving.
Common Mistakes to Avoid
When calculating the perimeter of a right triangle, there are several common mistakes that students and professionals often make. Being aware of these pitfalls can help ensure accurate and reliable results. Below is a list of common mistakes and how to avoid them:
-
Misidentifying the Hypotenuse:
One of the most frequent errors is confusing the hypotenuse with one of the legs. Remember, the hypotenuse is always the side opposite the right angle and is the longest side of the right triangle.
-
Incorrect Application of the Pythagorean Theorem:
Ensure that you correctly apply the Pythagorean theorem: \( a^2 + b^2 = c^2 \), where \( c \) is the hypotenuse. Double-check your calculations for squaring and square rooting.
-
Ignoring Units:
Units should be consistent throughout your calculation. Mixing units, such as using centimeters for one leg and meters for another, can lead to incorrect results. Always convert units to be the same before performing calculations.
-
Forgetting to Sum All Sides:
When calculating the perimeter, make sure to add the lengths of all three sides: \( P = a + b + c \). Forgetting to include one of the sides will result in an incomplete perimeter.
-
Using Approximate Values:
While approximations are sometimes necessary, using overly rounded values for the sides can lead to significant errors. Whenever possible, use precise values for the most accurate perimeter calculation.
-
Calculation Errors:
Simple arithmetic mistakes can lead to incorrect results. Carefully check each step of your calculation, especially when adding, subtracting, multiplying, or dividing numbers.
-
Incorrectly Measuring Sides:
Ensure that the sides of the triangle are measured accurately. Incorrect measurements will lead to incorrect perimeter calculations.
By paying attention to these common mistakes and taking steps to avoid them, you can ensure that your calculations for the perimeter of a right triangle are accurate and reliable.
Advanced Concepts
Delving deeper into the study of right triangles, there are several advanced concepts that can enhance your understanding and application of perimeter calculations. These concepts include advanced geometric properties, trigonometric relationships, and applications in various fields.
1. Using Trigonometric Ratios
Trigonometric ratios such as sine, cosine, and tangent can be utilized to find the sides of a right triangle when certain angles and sides are known. For example:
- Sine: \( \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \)
- Cosine: \( \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} \)
- Tangent: \( \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \)
Using these ratios, you can solve for unknown sides and then calculate the perimeter using the formula \( P = a + b + c \).
2. Heron's Formula for Right Triangles
Heron's formula can be adapted for right triangles to find the perimeter when the area is known. The area \( A \) of a right triangle can be calculated as:
\( A = \frac{1}{2} \times a \times b \)
Using Heron's formula, the semi-perimeter \( s \) is:
\( s = \frac{a + b + c}{2} \)
The area \( A \) can also be expressed as:
\( A = \sqrt{s \times (s - a) \times (s - b) \times (s - c)} \)
By solving for \( s \) and rearranging, you can verify the perimeter with the known sides.
3. Coordinate Geometry Applications
In coordinate geometry, the vertices of a right triangle can be placed on a coordinate plane, and the distance formula can be used to find the lengths of the sides:
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Once the lengths are determined, the perimeter can be calculated. This is particularly useful in fields such as computer graphics and engineering.
4. Perimeter in Non-Euclidean Geometry
In non-Euclidean geometry, such as spherical or hyperbolic geometry, the concepts of triangles and their perimeters are different. For example, on a sphere, the sum of the angles of a triangle exceeds 180 degrees. Advanced study in these areas involves understanding how the perimeter and other properties change with curvature.
5. Real-World Applications
Advanced applications of right triangle perimeter calculations can be found in various fields:
- Engineering: Structural design and analysis often involve right triangles for load distribution and stability.
- Computer Science: Algorithms for graphics rendering and spatial analysis use right triangle properties.
- Astronomy: Triangulation methods to determine distances to celestial objects.
By exploring these advanced concepts, you can gain a deeper understanding of the versatility and applications of right triangle perimeter calculations in various domains.
Practice Problems
Practice problems are essential for mastering the calculation of right triangle perimeters. Below are several problems of varying difficulty, complete with step-by-step solutions to help you understand the process.
Problem 1: Basic Perimeter Calculation
Given a right triangle with legs \( a = 3 \) units and \( b = 4 \) units, calculate the perimeter.
- First, use the Pythagorean theorem to find the hypotenuse \( c \): \[ c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Next, add the lengths of all three sides to find the perimeter \( P \): \[ P = a + b + c = 3 + 4 + 5 = 12 \, \text{units} \]
Problem 2: Perimeter with One Side and Hypotenuse
Given a right triangle with one leg \( a = 5 \) units and hypotenuse \( c = 13 \) units, calculate the perimeter.
- Use the Pythagorean theorem to find the other leg \( b \): \[ b = \sqrt{c^2 - a^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12 \]
- Next, add the lengths of all three sides to find the perimeter \( P \): \[ P = a + b + c = 5 + 12 + 13 = 30 \, \text{units} \]
Problem 3: Using Trigonometric Ratios
Given a right triangle with one leg \( a = 7 \) units and an angle \( \theta = 30^\circ \), calculate the perimeter.
- First, find the other leg \( b \) using the tangent function: \[ \tan(\theta) = \frac{a}{b} \implies b = \frac{a}{\tan(\theta)} = \frac{7}{\tan(30^\circ)} = \frac{7}{\frac{1}{\sqrt{3}}} = 7\sqrt{3} \]
- Next, find the hypotenuse \( c \) using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} = \sqrt{7^2 + (7\sqrt{3})^2} = \sqrt{49 + 147} = \sqrt{196} = 14 \]
- Finally, add the lengths of all three sides to find the perimeter \( P \): \[ P = a + b + c = 7 + 7\sqrt{3} + 14 \]
Problem 4: Word Problem
A ladder leans against a wall, forming a right triangle with the ground. The ladder is 10 feet long and touches the wall at a height of 8 feet. Find the distance from the base of the ladder to the wall and the perimeter of the triangle.
- Use the Pythagorean theorem to find the base \( b \): \[ b = \sqrt{c^2 - a^2} = \sqrt{10^2 - 8^2} = \sqrt{100 - 64} = \sqrt{36} = 6 \, \text{feet} \]
- Next, add the lengths of all three sides to find the perimeter \( P \): \[ P = a + b + c = 8 + 6 + 10 = 24 \, \text{feet} \]
Problem 5: Coordinate Geometry
Find the perimeter of a right triangle with vertices at \( (0, 0) \), \( (6, 0) \), and \( (0, 8) \) on the coordinate plane.
- Calculate the lengths of the legs using the distance formula: \[ a = \sqrt{(6 - 0)^2 + (0 - 0)^2} = 6 \] \[ b = \sqrt{(0 - 0)^2 + (8 - 0)^2} = 8 \]
- Find the hypotenuse \( c \) using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]
- Finally, add the lengths of all three sides to find the perimeter \( P \): \[ P = a + b + c = 6 + 8 + 10 = 24 \, \text{units} \]
These practice problems should help reinforce your understanding of right triangle perimeter calculations. Try solving similar problems to further enhance your skills.
Frequently Asked Questions
Below are some frequently asked questions about the perimeter of right triangles, along with detailed answers to help you understand the concepts better.
1. What is the formula for the perimeter of a right triangle?
The perimeter \( P \) of a right triangle is the sum of the lengths of all three sides. If the legs are \( a \) and \( b \), and the hypotenuse is \( c \), the formula is:
\( P = a + b + c \)
2. How do I find the hypotenuse of a right triangle?
To find the hypotenuse \( c \) of a right triangle, use the Pythagorean theorem:
\( c = \sqrt{a^2 + b^2} \)
Where \( a \) and \( b \) are the lengths of the legs.
3. Can I calculate the perimeter if only the hypotenuse and one leg are known?
Yes, if you know the hypotenuse \( c \) and one leg \( a \), you can find the other leg \( b \) using the Pythagorean theorem:
\( b = \sqrt{c^2 - a^2} \)
Then, use the perimeter formula:
\( P = a + b + c \)
4. What if the sides are given in different units?
If the sides are given in different units, you must convert them to the same unit before calculating the perimeter. Consistent units are crucial for accurate calculations.
5. How is the perimeter related to the area of a right triangle?
While the perimeter is the total distance around the triangle, the area \( A \) is calculated as:
\( A = \frac{1}{2} \times a \times b \)
Both measurements provide different information about the triangle's size.
6. What is the significance of the Pythagorean theorem in perimeter calculations?
The Pythagorean theorem is essential for finding the hypotenuse when the lengths of the legs are known. It ensures that the relationship between the sides of a right triangle is accurately maintained, allowing for precise perimeter calculations.
7. Are there any special types of right triangles?
Yes, some special right triangles have side lengths that follow specific ratios, such as the 3-4-5 triangle and the 5-12-13 triangle. These ratios make calculations simpler and can be useful for quick assessments.
8. How do trigonometric ratios help in finding the perimeter?
Trigonometric ratios like sine, cosine, and tangent relate the angles to the sides of the triangle. For example, if one angle and one side are known, you can use these ratios to find the other sides and then calculate the perimeter:
- \( \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \)
- \( \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} \)
- \( \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \)
9. Can the perimeter of a right triangle be a decimal or fraction?
Yes, the perimeter can be a decimal or fraction, depending on the lengths of the sides. Precision in measurement and calculation is essential to ensure accuracy.
10. What are some common mistakes to avoid when calculating the perimeter?
Some common mistakes include misidentifying the hypotenuse, incorrect application of the Pythagorean theorem, ignoring units, and arithmetic errors. Refer to the "Common Mistakes to Avoid" section for more details on avoiding these pitfalls.
By understanding these frequently asked questions, you can gain a better grasp of the principles and techniques involved in calculating the perimeter of right triangles.
Conclusion
In this article, we have explored the concept of the perimeter of a right triangle, delving into various components and steps involved in its calculation. By understanding the properties of right triangles and utilizing the Pythagorean Theorem, we can effectively derive and calculate the perimeter. Here's a summary of the key points covered:
- Understanding Right Triangles: Right triangles have one 90-degree angle, with the two other angles adding up to 90 degrees. The sides opposite these angles are known as the legs, and the side opposite the right angle is the hypotenuse.
- Components of a Right Triangle: The right triangle consists of two legs (a and b) and the hypotenuse (c).
- Basic Perimeter Formula: The perimeter (P) of a right triangle is the sum of its three sides: \( P = a + b + c \).
- Pythagorean Theorem: This fundamental theorem helps in calculating the hypotenuse: \( c = \sqrt{a^2 + b^2} \).
- Step-by-Step Calculation: To find the perimeter, first calculate the hypotenuse using the Pythagorean Theorem and then add all three sides.
- Example Calculations: We provided detailed examples illustrating the step-by-step process of finding the perimeter of right triangles.
- Applications: The knowledge of right triangle perimeters is applied in various fields such as architecture, engineering, and everyday problem-solving.
- Common Mistakes: Avoid errors such as incorrect calculation of the hypotenuse or misidentifying the legs and hypotenuse.
- Advanced Concepts: We touched on more complex scenarios involving right triangles, including special triangles and trigonometric relationships.
- Practice Problems: Provided a set of problems for practice to reinforce the understanding and calculation of right triangle perimeters.
- Frequently Asked Questions: Addressed common questions and clarified doubts regarding right triangle perimeters.
Understanding and accurately calculating the perimeter of right triangles is a foundational skill in geometry that has broad applications. By mastering the principles and methods discussed, you can confidently approach various mathematical and practical problems involving right triangles. Keep practicing and applying these concepts to enhance your mathematical proficiency.
Tìm hiểu về diện tích và chu vi của tam giác vuông với Thầy J. Video này sẽ hướng dẫn bạn cách tính diện tích và chu vi một cách chi tiết và dễ hiểu.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán học cùng Thầy J
READ MORE:
Hướng dẫn cách tìm diện tích và chu vi của tam giác vuông. Video này cung cấp phương pháp chi tiết và dễ hiểu để tính toán.
Cách Tìm Diện Tích và Chu Vi của Tam Giác Vuông