Topic formulas for area and perimeter of all shapes: Discover the essential formulas for calculating the area and perimeter of all shapes. This comprehensive guide covers everything from basic geometric figures to complex polygons and circles. Perfect for students, teachers, and math enthusiasts, this article simplifies learning with clear explanations and practical examples. Unlock the secrets of geometry and boost your mathematical skills today!
Table of Content
- Formulas for Area and Perimeter of All Shapes
- Introduction
- Basic Geometric Shapes
- Triangles
- Quadrilaterals
- Polygons
- Circles and Ellipses
- Composite Shapes
- Three-Dimensional Shapes
- Special Geometric Properties
- Applications of Area and Perimeter
- Tips and Tricks for Remembering Formulas
- Conclusion
- YOUTUBE: Tìm hiểu cách tính diện tích các hình hình học như hình chữ nhật, tam giác, hình tròn và cung tròn, hình thang, hình vuông, hình bình hành và hình thoi. Video hữu ích cho những ai muốn nắm vững công thức tính diện tích và chu vi các hình.
Formulas for Area and Perimeter of All Shapes
Triangle
- Area: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- Perimeter: \( P = a + b + c \) (sum of all sides)
Square
- Area: \( A = s^2 \) (side squared)
- Perimeter: \( P = 4s \) (four times the side)
Rectangle
- Area: \( A = l \times w \) (length times width)
- Perimeter: \( P = 2(l + w) \) (twice the sum of length and width)
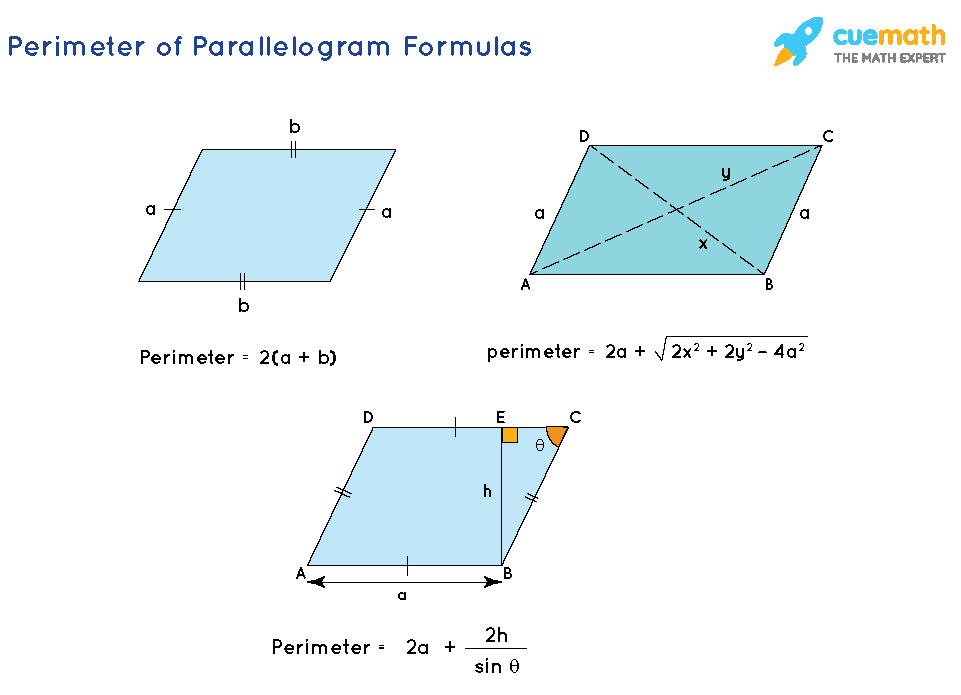
Parallelogram
- Area: \( A = b \times h \) (base times height)
- Perimeter: \( P = 2(a + b) \) (sum of all sides times two)
Rhombus
- Area: \( A = \frac{1}{2} \times d_1 \times d_2 \) (half the product of the diagonals)
Trapezoid
- Area: \( A = \frac{1}{2} \times (b_1 + b_2) \times h \) (half the sum of the bases times height)
- Perimeter: \( P = a + b_1 + b_2 + c \) (sum of all sides)
Circle
- Area: \( A = \pi r^2 \) (pi times radius squared)
- Circumference: \( C = 2\pi r \) (two times pi times radius)
Ellipse
- Area: \( A = \pi a b \) (pi times the product of the semi-major and semi-minor axes)
- Perimeter: \( P \approx \pi [3(a + b) - \sqrt{(3a + b)(a + 3b)}] \) (approximation)
Regular Polygon
- Area: \( A = \frac{1}{4} n s^2 \cot \left( \frac{\pi}{n} \right) \) (n sides, s side length)
- Perimeter: \( P = n \times s \) (number of sides times side length)
Summary Table
| Shape | Area | Perimeter/Circumference |
| Triangle | \( \frac{1}{2} \times \text{base} \times \text{height} \) | \( a + b + c \) |
| Square | \( s^2 \) | \( 4s \) |
| Rectangle | \( l \times w \) | \( 2(l + w) \) |
| Parallelogram | \( b \times h \) | \( 2(a + b) \) |
| Rhombus | \( \frac{1}{2} \times d_1 \times d_2 \) | \( 4s \) |
| Trapezoid | \( \frac{1}{2} \times (b_1 + b_2) \times h \) | \( a + b_1 + b_2 + c \) |
| Circle | \( \pi r^2 \) | \( 2\pi r \) |
| Ellipse | \( \pi a b \) | \( \pi [3(a + b) - \sqrt{(3a + b)(a + 3b)}] \) (approx.) |
| Regular Polygon | \( \frac{1}{4} n s^2 \cot \left( \frac{\pi}{n} \right) \) | \( n \times s \) |

READ MORE:
Introduction
Understanding the formulas for the area and perimeter of geometric shapes is fundamental to mastering geometry. These concepts are not only essential in mathematical studies but also have practical applications in various fields such as engineering, architecture, and everyday problem-solving.
In this guide, we will explore the formulas for calculating the area and perimeter of a wide range of geometric shapes, including basic shapes like triangles and rectangles, as well as more complex figures such as polygons, circles, and three-dimensional solids.
Here is a brief overview of what you will learn in this guide:
- Basic Geometric Shapes: Discover the simple formulas for the area and perimeter of squares, rectangles, and other basic shapes.
- Triangles: Learn about the different types of triangles and how to calculate their area and perimeter.
- Quadrilaterals: Understand the formulas for quadrilaterals, including parallelograms, trapezoids, and rhombuses.
- Polygons: Explore the methods to determine the area and perimeter of various polygons.
- Circles and Ellipses: Get to know the formulas for the circumference and area of circles, as well as the properties of ellipses.
- Composite Shapes: Learn how to calculate the area and perimeter of shapes that are combinations of simpler figures.
- Three-Dimensional Shapes: Delve into the surface area and volume calculations for solids like cubes, cylinders, cones, and spheres.
- Special Geometric Properties: Understand unique properties that affect area and perimeter calculations, such as the Pythagorean theorem and trigonometric ratios.
- Applications of Area and Perimeter: See how these formulas are used in real-life scenarios, from designing spaces to solving practical problems.
- Tips and Tricks for Remembering Formulas: Find helpful mnemonics and strategies to easily recall these essential formulas.
By the end of this guide, you will have a comprehensive understanding of the formulas for area and perimeter, enabling you to tackle a variety of geometric problems with confidence.
Basic Geometric Shapes
Understanding the basic geometric shapes is fundamental in learning geometry. Here are the essential formulas for calculating the area and perimeter of the most common basic shapes:
Square
- Perimeter: \( P = 4a \)
- Area: \( A = a^2 \)
Rectangle
- Perimeter: \( P = 2(l + w) \)
- Area: \( A = lw \)
Triangle
- Perimeter: \( P = a + b + c \)
- Area: \( A = \frac{1}{2}bh \)
Parallelogram
- Perimeter: \( P = 2(a + b) \)
- Area: \( A = bh \)
Rhombus
- Perimeter: \( P = 4a \)
- Area: \( A = \frac{1}{2}d_1d_2 \)
Trapezoid
- Perimeter: \( P = a + b + c + d \)
- Area: \( A = \frac{1}{2}(a + b)h \)
Circle
- Circumference: \( C = 2\pi r \)
- Area: \( A = \pi r^2 \)
Ellipse
- Perimeter (Approximate): \( P \approx \pi \left( 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right) \)
- Area: \( A = \pi ab \)
These formulas are the foundation for calculating the area and perimeter of basic geometric shapes. They are crucial for solving more complex geometry problems and understanding the properties of these shapes in various applications.
Triangles
Triangles are one of the most fundamental geometric shapes, characterized by having three sides, three vertices, and three angles. Here we explore the various formulas for calculating the area and perimeter of different types of triangles.
Area of a Triangle
The area of a triangle can be calculated using several different formulas, depending on the known parameters:
- Base and Height: The most common formula is:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}
\] - Three Sides (Heron's Formula): When the lengths of all three sides are known, the area can be calculated using Heron's formula. First, calculate the semi-perimeter:
Then, the area is:
\[
s = \frac{a + b + c}{2}
\]
\[
\text{Area} = \sqrt{s(s - a)(s - b)(s - c)}
\] - Two Sides and Included Angle: When two sides and the angle between them are known:
\[
\text{Area} = \frac{1}{2} \times a \times b \times \sin(C)
\] - Equilateral Triangle: For a triangle where all sides are equal:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2
\] - Isosceles Triangle: For a triangle with two equal sides:
\[
\text{Area} = \frac{1}{4} \times b \times \sqrt{4a^2 - b^2}
\]
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its sides:
\[
\text{Perimeter} = a + b + c
\]
For specific types of triangles, the formulas are simplified:
- Equilateral Triangle:
\[
\text{Perimeter} = 3a
\] - Isosceles Triangle:
\[
\text{Perimeter} = 2a + b
\]
Example Calculations
Here are some example calculations to illustrate the use of these formulas:
- Example 1: Find the area of a triangle with a base of 8 cm and a height of 5 cm.
\[
\text{Area} = \frac{1}{2} \times 8 \times 5 = 20 \text{ cm}^2
\] - Example 2: Find the area of an equilateral triangle with each side measuring 6 cm.
\[
\text{Area} = \frac{\sqrt{3}}{4} \times 6^2 = 9\sqrt{3} \text{ cm}^2
\]
Quadrilaterals
Quadrilaterals are four-sided polygons with a variety of types, each with unique properties and formulas for calculating their area and perimeter. Below, we discuss the formulas for some common types of quadrilaterals.
General Quadrilateral
For any quadrilateral, if the lengths of all sides and one diagonal are known, the area can be calculated by dividing the shape into two triangles:
- Area = \(\frac{1}{2} \times \text{diagonal} \times (\text{sum of heights of the two triangles})\)
Square
- Area = \(a^2\), where \(a\) is the length of a side.
- Perimeter = \(4a\)
Rectangle
- Area = \(l \times b\), where \(l\) is the length and \(b\) is the breadth.
- Perimeter = \(2(l + b)\)
Parallelogram
- Area = \(b \times h\), where \(b\) is the base and \(h\) is the height.
- Perimeter = \(2(a + b)\), where \(a\) and \(b\) are the lengths of the adjacent sides.
Rhombus
- Area = \(\frac{1}{2} \times d_1 \times d_2\), where \(d_1\) and \(d_2\) are the lengths of the diagonals.
- Perimeter = \(4a\), where \(a\) is the length of a side.
Kite
- Area = \(\frac{1}{2} \times d_1 \times d_2\), where \(d_1\) and \(d_2\) are the lengths of the diagonals.
- Perimeter = \(2(a + b)\), where \(a\) and \(b\) are the lengths of the pairs of adjacent sides.
Trapezium (Trapezoid)
- Area = \(\frac{1}{2} \times (a + b) \times h\), where \(a\) and \(b\) are the lengths of the parallel sides and \(h\) is the height.
- Perimeter = \(a + b + c + d\), where \(a\), \(b\), \(c\), and \(d\) are the lengths of the sides.
Quadrilaterals encompass a wide range of shapes, each with distinct properties and formulas for calculating area and perimeter. Understanding these basic formulas allows for solving various geometric problems involving these versatile shapes.

Polygons
A polygon is a closed two-dimensional shape with three or more straight sides. Polygons can be classified based on the number of sides and their properties into regular and irregular polygons, as well as convex and concave polygons.
Properties of Polygons
- The sum of the interior angles of a polygon with n sides is given by the formula: \( (n-2) \times 180^\circ \)
- A regular polygon has all sides and interior angles equal.
- An irregular polygon has sides and angles of different lengths and measures.
- A convex polygon has all interior angles less than 180°.
- A concave polygon has at least one interior angle greater than 180°.
Formulas for Polygons
Perimeter of a Regular Polygon
The perimeter of a regular polygon can be calculated using the formula:
\[ P = n \times s \]
where n is the number of sides and s is the length of one side.
Area of a Regular Polygon
The area of a regular polygon can be found using the formula:
\[ A = \frac{1}{2} \times P \times a \]
where P is the perimeter and a is the apothem (the distance from the center to the midpoint of a side).
Example Calculations
| Polygon | Number of Sides (n) | Length of Side (s) | Perimeter (P) | Apothem (a) | Area (A) |
|---|---|---|---|---|---|
| Hexagon | 6 | 10 cm | \( P = 6 \times 10 = 60 \) cm | 8.66 cm | \( A = \frac{1}{2} \times 60 \times 8.66 = 259.8 \) cm² |
| Octagon | 8 | 7 cm | \( P = 8 \times 7 = 56 \) cm | 5.79 cm | \( A = \frac{1}{2} \times 56 \times 5.79 = 162.12 \) cm² |
Interior and Exterior Angles
- The measure of each interior angle of a regular polygon is given by: \[ \frac{(n-2) \times 180^\circ}{n} \]
- The measure of each exterior angle of a regular polygon is: \[ \frac{360^\circ}{n} \]
Understanding these basic properties and formulas allows for the calculation of the perimeter and area of various regular polygons, which is fundamental in geometry.
Circles and Ellipses
Understanding the formulas for the area and perimeter of circles and ellipses is crucial in geometry. These shapes have unique properties and their calculations are essential in various applications.
Circle
A circle is a special type of ellipse where the major and minor axes are equal, making all points equidistant from the center.
- Area: The area \(A\) of a circle is calculated using the formula: \[ A = \pi r^2 \] where \(r\) is the radius of the circle.
- Perimeter: The perimeter (or circumference) \(C\) of a circle is given by: \[ C = 2\pi r \] where \(r\) is the radius.
Ellipse
An ellipse is a shape that generalizes a circle, characterized by two axes: the major axis and the minor axis. The major axis is the longest diameter, while the minor axis is the shortest.
- Area: The area \(A\) of an ellipse is calculated using the formula: \[ A = \pi a b \] where \(a\) is the length of the semi-major axis and \(b\) is the length of the semi-minor axis.
- Perimeter: The perimeter \(P\) of an ellipse is more complex to calculate exactly. However, an approximate formula is: \[ P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \] This approximation is generally within 5% of the true value, provided \(a\) is not more than three times \(b\).
These formulas provide the foundational calculations for these shapes, which are used in various fields such as engineering, architecture, and everyday problem-solving.
Composite Shapes
Composite shapes are figures that consist of two or more basic geometric shapes combined together. These shapes can be simple or complex, depending on the arrangement and type of shapes used. To find the area and perimeter of composite shapes, we need to break them down into their basic components.
Finding the Area of Composite Shapes
To calculate the area of a composite shape, follow these steps:
- Divide the composite shape into simpler shapes such as rectangles, triangles, circles, etc.
- Calculate the area of each simple shape using their respective formulas.
- Add the areas of the simple shapes to find the total area of the composite shape.
Let's consider an example:
- Composite Shape: A rectangle combined with a semicircle.
- Step 1: Divide the shape into a rectangle and a semicircle.
- Step 2: Calculate the area of the rectangle \(A_{\text{rect}} = l \times w\).
- Step 3: Calculate the area of the semicircle \(A_{\text{semi}} = \frac{1}{2} \pi r^2\).
- Step 4: Add the areas: \(A_{\text{total}} = A_{\text{rect}} + A_{\text{semi}}\).
Finding the Perimeter of Composite Shapes
To calculate the perimeter of a composite shape, follow these steps:
- Identify the outer edges of the composite shape.
- Calculate the perimeter of each segment that forms the outer boundary.
- Add the lengths of these segments to find the total perimeter.
Consider the same example of a rectangle with a semicircle:
- Step 1: Identify the outer edges: two sides of the rectangle and the curved part of the semicircle.
- Step 2: Calculate the perimeter of the rectangle's sides: \(P_{\text{rect sides}} = 2 \times (l + w)\).
- Step 3: Calculate the perimeter of the semicircle: \(P_{\text{semi}} = \pi r\).
- Step 4: Add the perimeters: \(P_{\text{total}} = P_{\text{rect sides}} + P_{\text{semi}}\).
Example Calculation
Let's apply these steps to a specific example:
| Shape | Dimensions | Formula | Calculation |
| Rectangle | Length = 8 cm, Width = 4 cm | \(A_{\text{rect}} = l \times w\) | \(8 \times 4 = 32 \, \text{cm}^2\) |
| Semicircle | Radius = 2 cm | \(A_{\text{semi}} = \frac{1}{2} \pi r^2\) | \(\frac{1}{2} \times 3.14 \times 2^2 = 6.28 \, \text{cm}^2\) |
| Total Area | \(32 + 6.28 = 38.28 \, \text{cm}^2\) | ||
Thus, the area of the composite shape is 38.28 square centimeters.
Three-Dimensional Shapes
Three-dimensional shapes, or 3D shapes, have depth in addition to width and height. This section covers the basic formulas for calculating the volume and surface area of common 3D shapes.
Cuboid (Rectangular Prism)
- Volume: \( V = l \times w \times h \)
where \( l \) is the length, \( w \) is the width, and \( h \) is the height.
- Surface Area: \( SA = 2lw + 2lh + 2wh \)
Sum of the areas of all six faces.
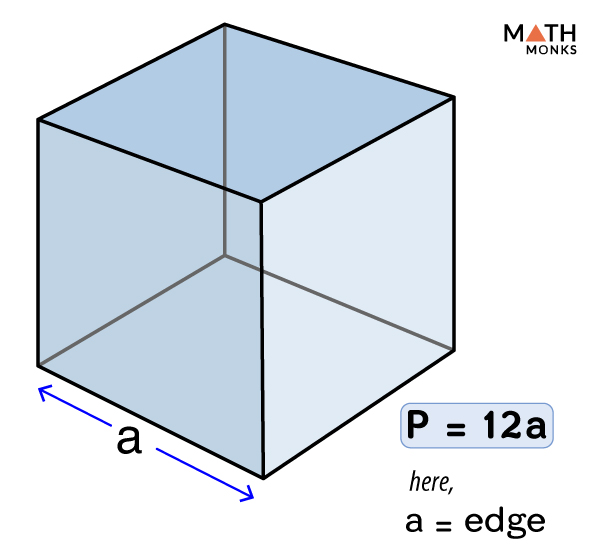
Cube
- Volume: \( V = a^3 \)
where \( a \) is the length of a side.
- Surface Area: \( SA = 6a^2 \)
Each of the six faces is a square with area \( a^2 \).
Cylinder
- Volume: \( V = \pi r^2 h \)
where \( r \) is the radius of the base, and \( h \) is the height.
- Surface Area: \( SA = 2\pi r (r + h) \)
Sum of the areas of the two bases and the curved surface.
Sphere
- Volume: \( V = \frac{4}{3} \pi r^3 \)
where \( r \) is the radius.
- Surface Area: \( SA = 4\pi r^2 \)
The area of the curved surface.
Cone
- Volume: \( V = \frac{1}{3} \pi r^2 h \)
where \( r \) is the radius of the base, and \( h \) is the height.
- Surface Area: \( SA = \pi r (r + l) \)
where \( l \) is the slant height. Sum of the area of the base and the curved surface.
Pyramid
- Volume: \( V = \frac{1}{3} A h \)
where \( A \) is the area of the base, and \( h \) is the height.
- Surface Area: The surface area depends on the shape of the base and the slant height of the pyramid's faces.

Special Geometric Properties
Understanding special geometric properties helps in solving various mathematical problems efficiently. Here are some key properties and formulas:
Properties of Triangles
- Sum of Interior Angles: The sum of the interior angles of a triangle is always \(180^\circ\).
- Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
- Pythagorean Theorem: In a right-angled triangle, \(a^2 + b^2 = c^2\), where \(c\) is the hypotenuse.
Properties of Quadrilaterals
- Parallelograms:
- Opposite sides are equal and parallel.
- Opposite angles are equal.
- Diagonals bisect each other.
- Rectangles:
- All angles are \(90^\circ\).
- Opposite sides are equal and parallel.
- Diagonals are equal in length.
- Squares:
- All sides are equal in length.
- All angles are \(90^\circ\).
- Diagonals are equal in length and bisect each other at \(90^\circ\).
Properties of Circles
- Radius: The distance from the center of the circle to any point on its circumference.
- Diameter: Twice the radius, the longest distance across the circle.
- Circumference: The perimeter of the circle, given by \(C = 2\pi r\).
- Area: The space enclosed by the circle, given by \(A = \pi r^2\).
Properties of Polygons
- Sum of Interior Angles: For an \(n\)-sided polygon, the sum of the interior angles is \((n-2) \times 180^\circ\).
- Regular Polygons: All sides and angles are equal. The measure of each interior angle of a regular \(n\)-sided polygon is \(\frac{(n-2) \times 180^\circ}{n}\).
Properties of Ellipses
- Major and Minor Axes: The longest and shortest diameters of the ellipse, respectively.
- Area: Given by \(A = \pi \times a \times b\), where \(a\) and \(b\) are the lengths of the semi-major and semi-minor axes.
- Circumference: Approximated by \(C \approx \pi \left( 3(a+b) - \sqrt{(3a+b)(a+3b)} \right)\).
By understanding these properties, one can better grasp the relationships and characteristics that define different geometric shapes and their applications.
Applications of Area and Perimeter
The concepts of area and perimeter are widely used in various real-life applications. Here are some detailed examples of their applications:
-
Construction and Architecture:
Architects and builders use area and perimeter calculations extensively when designing and constructing buildings. For instance, they calculate the area of rooms to determine the amount of flooring or paint required. Similarly, the perimeter is used to calculate the length of wiring or baseboards needed.
-
Landscaping and Agriculture:
In landscaping, calculating the area is essential for planning gardens, lawns, and other green spaces. Farmers use area measurements to determine the size of their fields to plan crop distribution, irrigation systems, and fencing (which also involves perimeter calculations).
-
Fencing and Paving:
When installing fences around properties or creating pavements and walkways, knowing the perimeter helps determine the total length of fencing material or the amount of paving material needed.
-
Interior Design:
Interior designers calculate the area of walls, floors, and ceilings to estimate the materials required for decorating or remodeling a space, such as wallpaper, tiles, or carpets.
-
Sports Fields:
The design and maintenance of sports fields involve calculating the area to ensure the field dimensions meet regulations. Additionally, perimeter measurements are used for planning the placement of boundary lines and seating arrangements.
-
Urban Planning:
Urban planners use area and perimeter calculations when designing city layouts, parks, and recreational areas. These measurements help in optimizing space usage and planning infrastructure.
-
Environmental Studies:
Calculating the area of forests, lakes, and other natural features is crucial for environmental conservation and management. These measurements help in monitoring changes in size due to natural or human activities.
-
Navigation and Mapping:
In cartography and navigation, area and perimeter calculations are used to create accurate maps. These measurements assist in determining distances and planning routes.
Below are some practical examples to illustrate the application of area and perimeter formulas:
| Scenario | Calculation |
|---|---|
| Fencing a Rectangular Garden |
Given a garden with a length of 20 meters and a width of 15 meters:
|
| Painting a Circular Wall |
Given a circular wall with a radius of 10 meters:
|
By understanding and applying these formulas, we can efficiently manage resources, plan projects, and solve practical problems in various fields.
Tips and Tricks for Remembering Formulas
Remembering geometric formulas for area and perimeter can be challenging, but with the right techniques, it becomes much easier. Here are some effective tips and tricks to help you recall these formulas:
-
Mnemonics: Create simple and memorable phrases to remember formulas. For example:
- "Cherry pies delicious!" for the circumference of a circle, \( C = \pi d \).
- "Apple pies are too!" for the area of a circle, \( A = \pi r^2 \).
- Visualization: Draw the shapes and label all known dimensions. This helps in understanding the relationship between the dimensions and the formulas.
- Relate to Real-World Objects: Associating shapes with real-world objects can make formulas more intuitive. For example, think of a square as a room and its perimeter as the length of the baseboards.
- Practice and Repetition: Regular practice is key. Solve a variety of problems involving these formulas to reinforce your memory.
- Chunking: Break down complex formulas into smaller parts. For instance, the area of a trapezoid can be remembered by dividing it into a rectangle and triangles.
- Songs and Rhymes: Use songs and rhymes to make learning fun. For example, use a rhyme for the area of a triangle: "Half the base times height gives the area right!" which translates to \( A = \frac{1}{2} \times \text{base} \times \text{height} \).
Quick Reference Table for Common Formulas
| Shape | Area Formula | Perimeter Formula |
|---|---|---|
| Square | \( A = s^2 \) | \( P = 4s \) |
| Rectangle | \( A = l \times w \) | \( P = 2(l + w) \) |
| Triangle | \( A = \frac{1}{2} \times \text{base} \times \text{height} \) | \( P = a + b + c \) |
| Circle | \( A = \pi r^2 \) | \( C = 2\pi r \) |
| Trapezoid | \( A = \frac{1}{2} \times (b_1 + b_2) \times h \) | \( P = a + b + c + d \) |
By incorporating these strategies into your study routine, you'll find it much easier to recall the necessary formulas for solving geometry problems.
Conclusion
Understanding the formulas for the area and perimeter of various geometric shapes is essential for solving many practical and theoretical problems. These concepts are fundamental in fields ranging from architecture and engineering to everyday tasks like home improvement and gardening.
The area is the measurement of the space enclosed within a shape, while the perimeter is the total distance around the shape. Different shapes have different formulas, and learning these can help in accurate calculations and better spatial understanding.
For instance, calculating the area of a rectangle requires the formula \( \text{Area} = l \times w \), where \( l \) is the length and \( w \) is the width. Similarly, the perimeter is calculated using \( \text{Perimeter} = 2(l + w) \). For circles, the area is given by \( \text{Area} = \pi r^2 \) and the circumference (perimeter) is \( \text{Circumference} = 2 \pi r \), where \( r \) is the radius.
These formulas are not only useful in academic settings but also have real-world applications. For example:
- In construction, knowing the area helps in determining the amount of materials needed, such as paint or flooring.
- In agriculture, farmers use these calculations to plan the layout of their fields and manage crop planting.
- In interior design, understanding these concepts assists in space planning and furniture arrangement.
Overall, mastering the formulas for area and perimeter equips you with valuable tools for a wide range of practical applications. As you continue to study and apply these concepts, you will find them increasingly intuitive and useful in both professional and everyday contexts.

Tìm hiểu cách tính diện tích các hình hình học như hình chữ nhật, tam giác, hình tròn và cung tròn, hình thang, hình vuông, hình bình hành và hình thoi. Video hữu ích cho những ai muốn nắm vững công thức tính diện tích và chu vi các hình.
Diện tích Hình chữ nhật, Tam giác, Hình tròn & Cung tròn, Hình thang, Hình vuông, Hình bình hành, Hình thoi, Hình học
READ MORE:
Tìm hiểu các công thức diện tích và chu vi của các hình học. Video này giúp bạn nắm vững cách tính diện tích và chu vi cho các hình học khác nhau một cách dễ dàng và chính xác.
Công thức Diện tích và Chu vi - Công thức Hình học