Topic how to find perimeter of a right triangle: Discover how to find the perimeter of a right triangle easily with our comprehensive guide. This article will walk you through the necessary steps, using clear examples and practical tips, to ensure you can calculate the perimeter accurately every time. Perfect for students, teachers, and anyone interested in geometry!
Table of Content
- How to Find the Perimeter of a Right Triangle
- Introduction to Right Triangles
- Understanding the Perimeter of a Triangle
- Identifying the Sides of a Right Triangle
- Using the Pythagorean Theorem
- Calculating the Hypotenuse
- Step-by-Step Guide to Finding the Perimeter
- Example Calculations
- Common Mistakes to Avoid
- Applications of Perimeter in Real Life
- Advanced Perimeter Calculations
- Practice Problems and Solutions
- Summary and Key Takeaways
- YOUTUBE:
How to Find the Perimeter of a Right Triangle
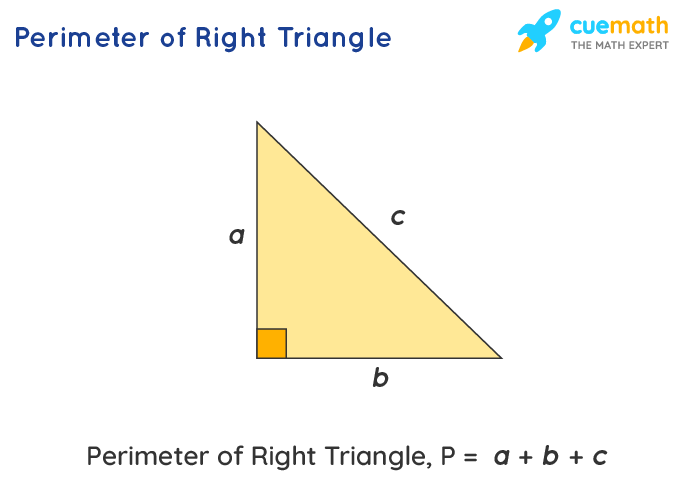
Finding the perimeter of a right triangle involves summing the lengths of all three sides. A right triangle has one right angle (90 degrees) and consists of three sides: the two legs (a and b) and the hypotenuse (c).
Steps to Find the Perimeter
Identify the lengths of the two legs: The legs are the two sides that form the right angle. Denote these as \( a \) and \( b \).
Calculate the hypotenuse: Use the Pythagorean theorem to find the length of the hypotenuse (c). The theorem states:
\[
c = \sqrt{a^2 + b^2}
\]Sum the side lengths: Add the lengths of the two legs and the hypotenuse to get the perimeter (P). The formula is:
\[
P = a + b + c
\]
Example
Suppose we have a right triangle with legs of lengths 3 and 4 units.
Identify the legs: \( a = 3 \), \( b = 4 \).
-
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] Find the perimeter:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Summary
To find the perimeter of a right triangle, follow these steps:
- Identify the lengths of the two legs (\( a \) and \( b \)).
- Calculate the hypotenuse (\( c \)) using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \).
- Add the lengths of all three sides to get the perimeter: \( P = a + b + c \).
This process ensures you accurately determine the perimeter of any right triangle.

READ MORE:
Introduction to Right Triangles
A right triangle is a type of triangle that has one angle measuring 90 degrees. This angle is called the right angle. The side opposite the right angle is the longest side and is known as the hypotenuse. The other two sides are called the legs of the triangle.
Right triangles are significant in geometry due to their unique properties and the ability to apply the Pythagorean Theorem, which is a fundamental principle used to calculate the lengths of the sides. Right triangles are also commonly found in various real-life applications such as architecture, engineering, and physics.
Properties of Right Triangles
- One angle is always 90 degrees.
- The side opposite the right angle is the hypotenuse.
- The other two sides are known as the legs.
Right Triangle Terminology
| Term | Definition |
|---|---|
| Right Angle | An angle that measures exactly 90 degrees. |
| Hypotenuse | The longest side of a right triangle, opposite the right angle. |
| Legs | The two sides that form the right angle. |
Understanding Right Triangles Through Examples
Consider a right triangle where one leg is 3 units long and the other leg is 4 units long. Using the Pythagorean Theorem, we can find the hypotenuse:
The Pythagorean Theorem states that in a right triangle:
\(a^2 + b^2 = c^2\)
Where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse. For our example:
\(3^2 + 4^2 = c^2\)
Which simplifies to:
\(9 + 16 = c^2\)
Therefore:
\(c^2 = 25\)
And taking the square root of both sides, we find:
\(c = 5\)
Thus, the hypotenuse of our right triangle is 5 units long.
Understanding the Perimeter of a Triangle
The perimeter of a triangle is the total length of its boundaries. For a right triangle, which has one 90-degree angle, the perimeter is the sum of the lengths of its three sides: the two legs and the hypotenuse. If we denote the legs as a and b, and the hypotenuse as c, the perimeter (P) can be calculated using the following formula:
\[ P = a + b + c \]
Steps to Calculate the Perimeter of a Right Triangle
- Identify the sides: Determine the lengths of the two legs (a and b) and the hypotenuse (c). If the hypotenuse is not given, it can be found using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \]
- Calculate the hypotenuse (if needed): Use the Pythagorean theorem to find the hypotenuse when only the legs are known. For example, if a = 3 and b = 4, then: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Sum the side lengths: Add the lengths of the two legs and the hypotenuse to get the perimeter. Using the previous example where a = 3, b = 4, and c = 5: \[ P = 3 + 4 + 5 = 12 \]
Example Calculation
Consider a right triangle with legs a = 6 units and b = 8 units:
- First, find the hypotenuse using the Pythagorean theorem: \[ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]
- Then, calculate the perimeter: \[ P = 6 + 8 + 10 = 24 \]
Key Points to Remember
- The perimeter is the sum of all sides of the triangle.
- Use the Pythagorean theorem to find the hypotenuse if it is not given.
- Ensure all side lengths are in the same unit before adding them.
Identifying the Sides of a Right Triangle
A right triangle is a type of triangle that has one angle measuring 90 degrees. This special property influences the names and relationships of its sides:
- Hypotenuse: The longest side, opposite the right angle. It is always the side that is not adjacent to the right angle.
- Adjacent: The side next to the right angle that is not the hypotenuse. This side is often referred to as the "base" of the triangle.
- Opposite: The side opposite to one of the non-right angles. This side is commonly referred to as the "height" or "perpendicular" side of the triangle.
To visualize these sides, consider the following right triangle with sides labeled as follows:
| Hypotenuse (c) | Adjacent (a) | Opposite (b) |
The relationship between these sides is defined by the Pythagorean Theorem, which states:
\[ c^2 = a^2 + b^2 \]
Using this theorem, you can determine any missing side if the lengths of the other two sides are known:
- If you know the lengths of the adjacent and opposite sides, you can find the hypotenuse:
- If you know the hypotenuse and one other side, you can find the remaining side:
\[ c = \sqrt{a^2 + b^2} \]
\[ a = \sqrt{c^2 - b^2} \] or \[ b = \sqrt{c^2 - a^2} \]
Understanding these basic properties and relationships is crucial for solving problems involving right triangles, whether you're calculating perimeters, areas, or simply identifying side lengths.
Using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry that relates the lengths of the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be written as:
\[ c^2 = a^2 + b^2 \]
Where:
- c is the length of the hypotenuse
- a and b are the lengths of the other two sides
Steps to Use the Pythagorean Theorem
- Identify the lengths of the two legs (a and b) of the right triangle.
- Square both of these lengths: \( a^2 \) and \( b^2 \).
- Add the squares of these lengths: \( a^2 + b^2 \).
- Take the square root of the sum to find the length of the hypotenuse: \( c = \sqrt{a^2 + b^2} \).
Example Calculation
Consider a right triangle where one leg is 3 units long and the other leg is 4 units long. To find the hypotenuse:
- Square the lengths of the legs:
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- Add these squares:
- \( 9 + 16 = 25 \)
- Take the square root of the sum to find the hypotenuse:
- \( \sqrt{25} = 5 \)
Thus, the hypotenuse of the triangle is 5 units long.
Applications of the Pythagorean Theorem
The Pythagorean Theorem is used in various fields such as:
- Construction and Engineering: To determine the lengths of sides in building and designing structures.
- Navigation: To find the shortest path between two points.
- Computer Graphics: To calculate distances between points on a screen.
Practice Problems
- A right triangle has legs of lengths 6 units and 8 units. Find the length of the hypotenuse.
- A ladder is leaning against a wall, with the base of the ladder 4 feet away from the wall and the top of the ladder 12 feet above the ground. How long is the ladder?
Try solving these problems using the steps outlined above to become proficient with the Pythagorean Theorem.
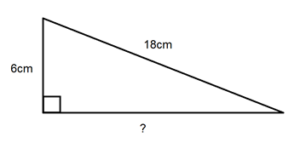
Calculating the Hypotenuse
Calculating the hypotenuse of a right triangle is a fundamental task in geometry, which can be accomplished using the Pythagorean Theorem. The hypotenuse is the longest side of a right triangle and is always opposite the right angle.
Here is a step-by-step guide to calculating the hypotenuse:
- Understand the Pythagorean Theorem: The theorem states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b):
\[ c^2 = a^2 + b^2 \]
- Identify the lengths of the legs: Measure or identify the lengths of the two legs of the triangle. For example, let’s say we have:
- Leg a = 3 cm
- Leg b = 4 cm
- Plug the values into the formula: Substitute the lengths of the legs into the Pythagorean theorem:
\[ c^2 = 3^2 + 4^2 \]
- Calculate the squares: Compute the squares of the lengths of the legs:
\[ c^2 = 9 + 16 \]
- Sum the squares: Add the results:
\[ c^2 = 25 \]
- Take the square root: Finally, find the square root of the sum to get the length of the hypotenuse:
\[ c = \sqrt{25} = 5 \text{ cm} \]
Thus, the hypotenuse of a right triangle with legs of 3 cm and 4 cm is 5 cm.
There are also other methods to find the hypotenuse if different parameters are known:
- Given one leg and an angle: Use trigonometric functions such as sine or cosine:
- If leg \( a \) and angle \( \beta \) are known: \[ c = \frac{a}{\cos(\beta)} \]
- If leg \( b \) and angle \( \alpha \) are known: \[ c = \frac{b}{\sin(\alpha)} \]
- Given one leg and the area: Use the formula for the area of a right triangle \( A = \frac{1}{2} a b \):
- Solve for the missing leg: \[ b = \frac{2A}{a} \]
- Then use the Pythagorean Theorem: \[ c = \sqrt{a^2 + b^2} \]
These methods provide flexible ways to determine the hypotenuse depending on the given information.
Step-by-Step Guide to Finding the Perimeter
Finding the perimeter of a right triangle involves adding the lengths of all three sides. Here is a detailed step-by-step guide to help you calculate it:
-
Identify the Sides of the Right Triangle:
- Leg a - One of the two shorter sides.
- Leg b - The other shorter side.
- Hypotenuse c - The longest side opposite the right angle.
-
Use the Pythagorean Theorem (if needed):
If you only know the lengths of the two legs (a and b), use the Pythagorean Theorem to find the hypotenuse:
\[
c = \sqrt{a^2 + b^2}
\] -
Calculate the Perimeter:
Once you have the lengths of all three sides, add them together to find the perimeter:
\[
P = a + b + c
\]
Here's an example to illustrate these steps:
Example:
- Given: \(a = 3\), \(b = 4\)
- Step 1: Use the Pythagorean Theorem to find \(c\): \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Step 2: Calculate the perimeter: \[ P = 3 + 4 + 5 = 12 \]
Therefore, the perimeter of the right triangle with sides 3, 4, and 5 is 12 units.
Example Calculations
Understanding how to calculate the perimeter of a right triangle can be solidified with a few examples. Here are detailed example calculations to guide you:
Example 1: Simple Calculation
Find the perimeter of a right-angled triangle if its base is 3 units, height is 4 units, and hypotenuse is 5 units.
- Given: base = 3 units, height = 4 units, hypotenuse = 5 units
- Perimeter \(P\) is calculated as the sum of all three sides:
- \[ P = \text{base} + \text{height} + \text{hypotenuse} \]
- \[ P = 3 + 4 + 5 = 12 \text{ units} \]
Example 2: Finding the Hypotenuse
Find the perimeter of a right-angled triangle if the base is 6 units and the height is 8 units.
- Given: base = 6 units, height = 8 units
- First, calculate the hypotenuse using the Pythagorean theorem:
- \[ (\text{Hypotenuse})^2 = (\text{Base})^2 + (\text{Height})^2 \]
- \[ (\text{Hypotenuse})^2 = 6^2 + 8^2 \]
- \[ (\text{Hypotenuse})^2 = 36 + 64 = 100 \]
- \[ \text{Hypotenuse} = \sqrt{100} = 10 \text{ units} \]
- Now, calculate the perimeter:
- \[ P = 6 + 8 + 10 = 24 \text{ units} \]
Example 3: Given Hypotenuse and One Side
Find the perimeter of a right-angled triangle if the base is 5 units and the hypotenuse is 13 units.
- Given: base = 5 units, hypotenuse = 13 units
- First, calculate the height using the Pythagorean theorem:
- \[ (\text{Hypotenuse})^2 = (\text{Base})^2 + (\text{Height})^2 \]
- \[ 13^2 = 5^2 + (\text{Height})^2 \]
- \[ 169 = 25 + (\text{Height})^2 \]
- \[ (\text{Height})^2 = 144 \]
- \[ \text{Height} = \sqrt{144} = 12 \text{ units} \]
- Now, calculate the perimeter:
- \[ P = 5 + 12 + 13 = 30 \text{ units} \]
Example 4: Given Only Base and Height
Find the perimeter of a right-angled triangle with a base of 9 units and a height of 12 units.
- Given: base = 9 units, height = 12 units
- First, calculate the hypotenuse using the Pythagorean theorem:
- \[ (\text{Hypotenuse})^2 = 9^2 + 12^2 \]
- \[ (\text{Hypotenuse})^2 = 81 + 144 = 225 \]
- \[ \text{Hypotenuse} = \sqrt{225} = 15 \text{ units} \]
- Now, calculate the perimeter:
- \[ P = 9 + 12 + 15 = 36 \text{ units} \]
Common Mistakes to Avoid
When calculating the perimeter of a right triangle, there are several common mistakes that students often make. Understanding these mistakes can help you avoid them and ensure your calculations are accurate. Here are the most frequent errors and how to prevent them:
- Misidentifying the Sides:
In a right triangle, the sides consist of two legs and the hypotenuse. Ensure you correctly identify the hypotenuse, which is the longest side opposite the right angle.
- Incorrect Use of the Pythagorean Theorem:
The Pythagorean theorem states \(a^2 + b^2 = c^2\), where \(c\) is the hypotenuse. Make sure to square the lengths of the legs, add them, and then take the square root to find the hypotenuse.
- Omitting the Hypotenuse in Perimeter Calculation:
The perimeter of a right triangle is the sum of all three sides. Don’t forget to include the hypotenuse in your final addition.
- Arithmetic Errors:
Carefully check your addition and square root calculations. Small arithmetic mistakes can lead to incorrect results.
- Unit Consistency:
Ensure all side lengths are in the same unit before performing calculations. Mixing units can result in incorrect perimeter values.
- Misinterpreting Problem Statements:
Read problem statements carefully. Ensure you understand which sides are given and what is required to find the missing side and the perimeter.
- Rounding Errors:
Be mindful of rounding intermediate results. It’s best to round only the final answer to avoid cumulative errors.
By being aware of these common mistakes, you can enhance your problem-solving skills and accurately determine the perimeter of right triangles.

Applications of Perimeter in Real Life
Understanding the perimeter of a right triangle has numerous practical applications in various fields. Here are some examples of how calculating the perimeter can be useful in real life:
-
Construction and Architecture:
In construction, the perimeter of right triangles is often used to determine the length of materials needed. For example, when creating triangular roof trusses, the total length of the edges needs to be measured accurately to cut the materials properly. Similarly, knowing the perimeter helps in installing triangular tiles or panels.
-
Landscaping:
Landscapers frequently deal with triangular plots or features. Knowing the perimeter of these triangular sections can help in planning fences, garden beds, or irrigation systems. For instance, if you want to fence a triangular garden plot, calculating the perimeter will tell you the total length of the fencing material required.
-
Navigation and Mapping:
In navigation and mapping, right triangles are often used in triangulation methods to determine distances and locations. Calculating the perimeter can assist in estimating travel distances or mapping out triangular sections of land.
-
Textile and Fashion Design:
In textile and fashion design, triangular patterns are common. Knowing the perimeter of these patterns helps designers ensure they have enough fabric for their designs. For instance, creating a triangular scarf or a dress with triangular elements requires precise perimeter calculations to cut the fabric accurately.
-
Sports and Recreation:
In sports, especially those involving fields or courts, understanding the perimeter of triangular sections can be crucial. For instance, setting up a volleyball net on a beach where the court forms a triangular shape due to obstacles or terrain requires knowing the perimeter to properly position the net and boundaries.
These examples illustrate how the concept of the perimeter of a right triangle is not just a theoretical mathematical problem but a practical tool that aids in various real-world applications.
Advanced Perimeter Calculations
Calculating the perimeter of a right triangle involves adding the lengths of all three sides. While basic calculations using the Pythagorean theorem are straightforward, advanced perimeter calculations may include additional elements and scenarios. Below are some detailed steps and methods for advanced perimeter calculations:
1. Given Sides \(a\) and \(b\)
When the two legs of the triangle, \(a\) and \(b\), are known, you can find the hypotenuse \(c\) and then the perimeter \(P\).
- Use the Pythagorean theorem to find the hypotenuse \(c\): \[ c = \sqrt{a^2 + b^2} \]
- Calculate the perimeter \(P\): \[ P = a + b + c \]
2. Given Sides \(a\) and \(c\)
When one leg and the hypotenuse are known, you can find the other leg \(b\) and then the perimeter \(P\).
- Find the other leg \(b\): \[ b = \sqrt{c^2 - a^2} \]
- Calculate the perimeter \(P\): \[ P = a + b + c \]
3. Given Sides \(b\) and \(c\)
When one leg and the hypotenuse are known, you can find the other leg \(a\) and then the perimeter \(P\).
- Find the other leg \(a\): \[ a = \sqrt{c^2 - b^2} \]
- Calculate the perimeter \(P\): \[ P = a + b + c \]
4. Perimeter in Terms of Area and Altitudes
Using the area \(A\) and the triangle’s altitudes, additional advanced calculations can be performed.
- Area \(A\) of a right triangle: \[ A = \frac{1}{2} \cdot a \cdot b \]
- Altitudes: \[ h_a = b, \quad h_b = a, \quad h_c = \frac{a \cdot b}{c} \]
- Semiperimeter \(s\): \[ s = \frac{a + b + c}{2} \]
5. Example Calculation
For a right triangle with sides \(a = 3\), \(b = 4\), and \(c = 5\):
- Calculate the hypotenuse \(c\): \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Calculate the perimeter \(P\): \[ P = 3 + 4 + 5 = 12 \]
6. Special Considerations
- Always double-check calculations to avoid rounding errors and ensure accuracy.
- Consider using software tools for complex calculations involving trigonometry and advanced geometry.
Practice Problems and Solutions
To master the concept of finding the perimeter of a right triangle, it's essential to practice with various problems. Below are some practice problems along with their solutions. Use these to test your understanding and enhance your skills.
-
Problem 1: Find the perimeter of a right triangle with a base of 6 units and a height of 8 units.
Solution:
- Calculate the hypotenuse using the Pythagorean theorem:
- Find the perimeter by summing all sides:
\[ c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ units} \]
\[ \text{Perimeter} = a + b + c = 6 + 8 + 10 = 24 \text{ units} \]
-
Problem 2: In a right triangle, the base is 5 units and the hypotenuse is 13 units. Find the perimeter.
Solution:
- Find the height using the Pythagorean theorem:
- Calculate the perimeter:
\[ c^2 = a^2 + b^2 \Rightarrow 13^2 = 5^2 + b^2 \Rightarrow 169 = 25 + b^2 \Rightarrow b^2 = 144 \Rightarrow b = 12 \text{ units} \]
\[ \text{Perimeter} = a + b + c = 5 + 12 + 13 = 30 \text{ units} \]
-
Problem 3: The legs of a right triangle are 7 units and 24 units. Find the perimeter.
Solution:
- Determine the hypotenuse:
- Sum all sides to get the perimeter:
\[ c = \sqrt{a^2 + b^2} = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \text{ units} \]
\[ \text{Perimeter} = a + b + c = 7 + 24 + 25 = 56 \text{ units} \]
-
Problem 4: A right triangle has one leg measuring 9 units and the hypotenuse measuring 15 units. Find the perimeter.
Solution:
- Use the Pythagorean theorem to find the other leg:
- Calculate the perimeter:
\[ c^2 = a^2 + b^2 \Rightarrow 15^2 = 9^2 + b^2 \Rightarrow 225 = 81 + b^2 \Rightarrow b^2 = 144 \Rightarrow b = 12 \text{ units} \]
\[ \text{Perimeter} = a + b + c = 9 + 12 + 15 = 36 \text{ units} \]
These problems provide a solid foundation for understanding how to calculate the perimeter of a right triangle. Practice these and similar problems to become more proficient in applying the Pythagorean theorem and calculating perimeters.
Summary and Key Takeaways
Finding the perimeter of a right triangle involves understanding the properties of the triangle and using the Pythagorean Theorem to determine the lengths of its sides. Below are the key points and steps to remember:
- A right triangle has one 90-degree angle and two other angles that sum up to 90 degrees.
- The three sides of a right triangle are known as the hypotenuse, the opposite, and the adjacent.
- The hypotenuse is the longest side and is opposite the right angle.
- The Pythagorean Theorem states that \( a^2 + b^2 = c^2 \), where \( c \) is the hypotenuse and \( a \) and \( b \) are the other two sides.
- To find the perimeter of a right triangle, add the lengths of all three sides: \( \text{Perimeter} = a + b + c \).
Step-by-step guide to finding the perimeter:
- Identify the lengths of the two shorter sides, \( a \) and \( b \).
- Calculate the length of the hypotenuse using the Pythagorean Theorem: \( c = \sqrt{a^2 + b^2} \).
- Add all three sides to find the perimeter: \( \text{Perimeter} = a + b + c \).
Example calculation:
| Side \( a \) | 3 units |
| Side \( b \) | 4 units |
| Hypotenuse \( c \) | \( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units |
| Perimeter | \( 3 + 4 + 5 = 12 \) units |
Key takeaways:
- Understand the basic properties of right triangles.
- Use the Pythagorean Theorem to find the hypotenuse.
- Sum the lengths of all three sides to determine the perimeter.
- Practice with various examples to become proficient in these calculations.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán Học với Thầy J
READ MORE:
Cách Tinh Tế Để Tìm Chu Vi của Tam Giác Vuông | (Giải Thích Từng Bước) | #toán #maths